当前位置：首页 > news >正文

动态规划——斜率优化DP

news 来源：原创 2025/5/19 3:03:39

题目清单

在这里插入图片描述

acwing300.任务安排1

状态表示f[i]:
集合：完成前i个任务且第i个任务为最后一个批次最后一个任务的方案。
属性：min
状态计算：
$f[i]=min\{f[j]+sumt[i] ×\sum_{j+1}^{i}w[u]+s×\sum_{j+1}^{n}w[i]\}$ $(0\leq j < i)$
$f[i]=min\{f[j]+sumt[i] ×(sumc[i]-sumc[j])+s×(sumc[n]-sumc[j])\}$ $(0\leq j < i)$

时间复杂度为 $O(n^2)$

#include <iostream>
#include <cstring>
using namespace std;
const int N = 5010;
typedef long long ll;
ll f[N];
ll sumt[N], sumc[N];
int n, s;
int main()
{cin >> n >> s;for (int i = 1; i <= n; i ++ ){scanf("%lld%lld", &sumt[i], &sumc[i]);sumt[i] += sumt[i - 1];sumc[i] += sumc[i - 1];}memset(f, 0x3f, sizeof f);f[0] = 0;for (int i = 1; i <= n; i ++ ){for (int j = 0; j < i; j ++ ){f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));}}cout << f[n];return 0;
}

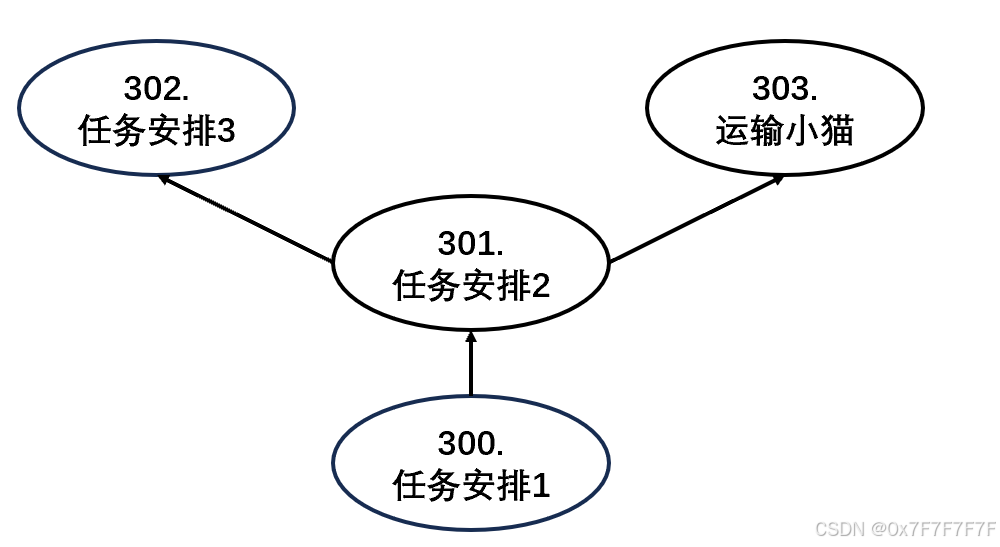
acwing301.任务安排2

我们对上一题得到的状态转移方程 $f[i]=min\{f[j]+sumt[i] ×(sumc[i]-sumc[j])+s×(sumc[n]-sumc[j])\}$ $(0\leq j < i)$ 进行编变形。

$f [i] = f [j] + s u m t [i] \times s u m c [i] - s u m t [i] \times s u m c [j] + s \times s u m c [n] - s \times s u m c [j]$
$f [i] = f [j] - s u m t [i] \times s u m c [j] - s \times s u m c [j] + s u m t [i] \times s u m c [i] + s \times s u m c [n]$
$f [i] = f [j] - (s u m t [i] + s) \times s u m c [j] + s u m t [i] \times s u m c [i] + s \times s u m c [n]$
移项得到
$f [j] = (s u m t [i] + s) \times s u m c [j] - s u m t [i] \times s u m c [i] - s \times s u m c [n] + f [i]$
上式是 $y = k x + b$ 的形式， $y$ 是 $f [j]$ , $k$ 是 $(s u m t [i] + s)$ , $x$ 是 $s u m c [j]$ , $b$ 是 $f [i] - s u m t [i] \times s u m c [i] - s \times s u m c [n]$ 。

我们的目标是求 $f [i]$ 的最小值，因为 $b$ 中除了 $f [i]$ 以外的部分是常量，也正因此等价于去想办法让截距最小。因为 $k$ 也是一个常量，所以本问题又可以转化为给定一条斜率固定的直线去找过一个 $(x, y)$ 点对,使得 $b$ 最小。 $(x, y)$ 点对有 $(s u m c [0], f [0])$ ， $(s u m c [1], f [1])$ ,…, $(s u m c [i - 1], f [i - 1])$ 。

给出结论，无论斜率如何变化，最小值一定是取到凸包下边界的一个点。
具体来说，最小值一定是第一个大于直线斜率的线段头部 $k_i$ 的点。

分析题目：
1., $k$ 是 $(s u m t [i] + s)$ ,单调递增。
2.新加入点的横坐标也是单调递增。
由于斜率 $k$ 是单调递增的，也就是说，如果当前的斜率 $k$ 大于队头两个点的斜率时，那么一开始的点就可以彻底删除，在以后也不会用到，所以凸包中的点可以用单调队列来维护。

维护一个凸包的做法：
1.查询的时候，把队头小于当前斜率k的点删掉。
$\frac{f[q[hh+1]-f[q[hh]}{sumc[q[hh+1]]-sumc[q[hh]}\leq sumt[i]+s$
2.插入的时候，把不在凸包上的点删掉。
$\frac{f[q[tt]-f[q[tt-1]}{sumc[q[hh]]-sumc[q[hh-1]}\geq \frac{f[i]-f[q[tt]]}{sumc[i]-sumc[q[hh]]}$

时间复杂度为 $O (n)$

#include <iostream>
using namespace std;
typedef long long ll;
const int N = 300010;
int q[N];
ll t[N], c[N];
ll f[N];
int n, s;
int main()
{cin >> n >> s;for (int i = 1; i <= n; i ++ ){scanf("%lld%lld", &t[i], &c[i]);t[i] += t[i - 1];c[i] += c[i - 1];}int hh = 0, tt = 0;for (int i = 1; i <= n; i ++ ){while (hh < tt && f[q[hh + 1]] - f[q[hh]] <= (t[i] + s) * (c[q[hh + 1]] - c[q[hh]])) hh ++ ;int j = q[hh];f[i] = f[j] + t[i] * (c[i] - c[j]) + s * (c[n] - c[j]);while (hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt -- ;q[++ tt] = i;}cout << f[n];return 0;
}

acwing302.任务安排3

和上一题不同的是，本题中机器的工作时间可以为负数，也正因此斜率 $k$ 并不是随着 $i$ 单调递增的了，上一题中，对于凸包的头部和尾部均使用单调队列来处理，本题则需要使用二分去找到合适的点对，对尾部的处理同样使用单调队列。

#include <iostream>
using namespace std;
const int N = 300010;
typedef long long ll;
ll t[N], c[N];
ll f[N];
int q[N];
int n, s;
int main()
{cin >> n >> s;for (int i = 1; i <= n; i ++ ){scanf("%lld%lld", &t[i], &c[i]);t[i] += t[i - 1];c[i] += c[i - 1];}int hh = 0, tt = 0;for (int i = 1; i <= n; i ++ ){int l = hh, r = tt;while (l < r){int mid = l + r >> 1;if (f[q[mid + 1]] - f[q[mid]] > (double)(t[i] + s) * (c[q[mid + 1]] - c[q[mid]])) r = mid;else l = mid + 1;}int j = q[l];f[i] = f[j] - (t[i] + s) * c[j] + t[i] * c[i] + s * c[n];while (hh < tt && (double)(f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (double)(f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt -- ;q[++ tt] = i;}cout << f[n];return 0;
}

acwing303.运输小猫

每一只小猫都会对应一个最早出发时间 $a [i] = t [i] - d [h [i]]$ ，也就是结束玩耍的时间减去到1号山的距离。当我们处理完 $a$ 数组后，对数组 $a$ 进行一个从小打到的排序。这样一来，相邻一段猫肯定是要由一个饲养员接走的，饲养员的出发时间就是这一段最后一只猫对应的数组 $a$ 的值。
状态表示f[i][j]:
集合：对于前 $i$ 只猫，安排 $j$ 个饲养员去接猫的所有方案。
属性：min
状态计算：
$f[i][j]=min\{f[k][j-1]+\sum_{k+1}^{i}(a_i-a_u)\}$ $\ \ \ (0\leq k <i)$
$f[i][j]=min\{f[k][j-1]+\sum_{k+1}^{i}a_i-\sum_{k+1}^{i}a_u\}$ $\ \ \ (0\leq k <i)$
$f[i][j]=min\{f[k][j-1]+(i-k)a_i-(s[i]-s[k])\}$ $\ \ \ (0\leq k <i)$
移项得:
$f [k] [j - 1] + s [k] = a [i] \times k + f [i] [j] + s [i] - ia [i]$
至此，本题就转换为了任务安排2。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 100010;
const int P = 110;
ll f[P][N];
ll a[N];
ll s[N];
int d[N];
int q[N];
int n, m, p;
ll get_y(int j, int k)
{return f[j - 1][k] + s[k];
}
int main()
{cin >> n >> m >> p;for (int i = 2; i <= n; i ++ ){scanf("%d", &d[i]);d[i] += d[i - 1];}for (int i = 1; i <= m; i ++ ){ll h, t;scanf("%lld%lld", &h, &t);a[i] = t - d[h];}sort(a + 1, a + m + 1);for (int i = 1; i <= m; i ++ ){s[i] = a[i];s[i] += s[i - 1];}memset(f,0x3f,sizeof f);for(int i = 0;i <= p;i ++)f[i][0] = 0;for (int i = 1; i <= p; i ++ ){int hh = 0, tt = 0;for (int j = 1; j <= m; j ++ ){while (hh < tt && get_y(i, q[hh + 1]) - get_y(i, q[hh]) <= (q[hh + 1] - q[hh]) * a[j]) hh ++;int k = q[hh];f[i][j] = f[i - 1][k] + (j - k) * a[j] - (s[j] - s[k]);while (hh < tt && (get_y(i, q[tt]) - get_y(i, q[tt - 1])) * (j - q[tt]) >= (get_y(i, j) - get_y(i, q[tt])) * (q[tt] - q[tt - 1])) tt --;q[++ tt] = j;}}cout << f[p][m];return 0;
}

题目清单

相关文章：