9.机器学习--SVM支持向量机

        支持向量机（Support Vector Machine，SVM）是一种二分类监督学习模型。支持向量机最早在 1964 年被提出，1995年前后理论成熟并开始被大量应用与人像识别、文本分类等问题中。它的基本模型是定义在特征空间上的间隔最大的线性分类器，这有区别与感知机。SVM 通过核技巧变成了实质上的非线性分类器。在 SVM 中学习的目的可以理解为求解凸二次规划的最优化算法。

目录

1.支持向量

2.最优化问题

3.对偶性

4.SVM优化 

5.软间隔

6.核函数

7.优缺点

8.示例代码

---

1.支持向量

首先我们来看一下在二维空间中线性可分数据是什么样的。在二维空间中，两类可以被一条直线（实际上也可以被称之为一维“平面”）完全分开的点被称之为线性可分。

在三维空间中，分割的方法变成了用一个面（也就是二维平面）进行分割。

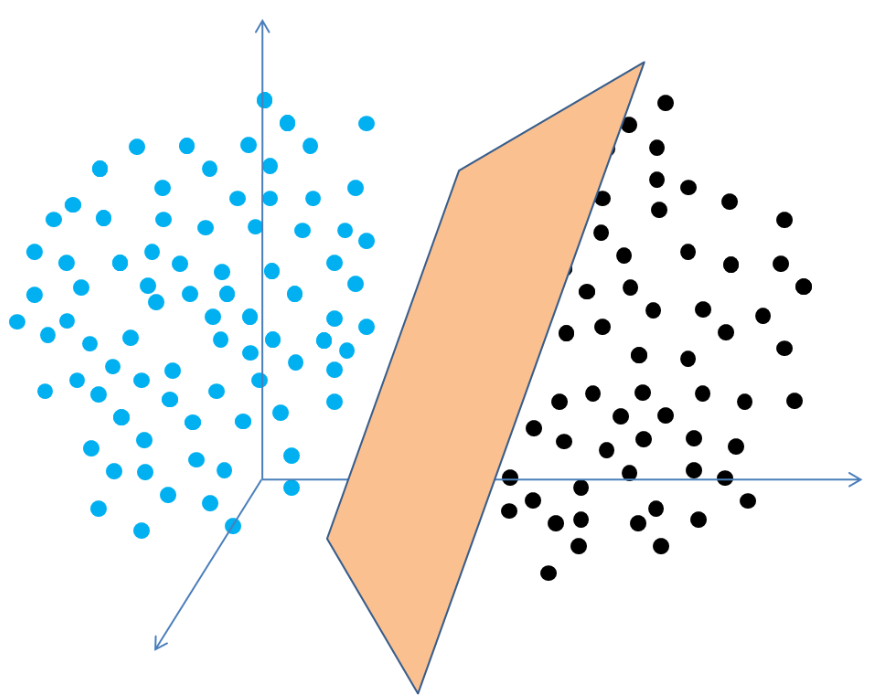
分割的过程在数学上可以被这样定义：

D0​ 和 D1​ 是 n 维欧式空间中的两个点击。如果存在 n 维向量 w 和实数 b，使得所有属于 D0​ 的点 xi​ 都有 wxi​+b>0，而对于所有属于 D1​ 的点 xj​ 则有 wxj​+b<0，则我们称 D0​ 和 D1​ 线性可分。

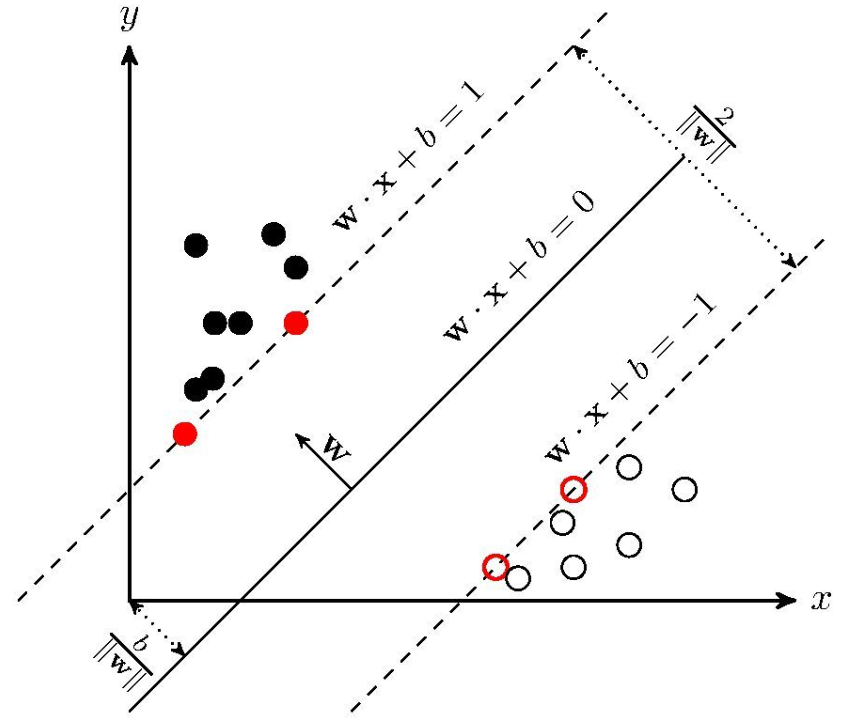
通俗的来说，我们在 n 维空间中可以使用一个 n−1 维的超平面进行分割。为了使这个超平面具有最佳鲁棒性，我们通常会寻找一个可以以最大间隔将两类样本分开的超平面（最大间隔也意味着具有更高的容错率），两侧距离超平面最近的点到超平面的距离被最大化了。

在上面一段定义中，我们提到了两侧距离超平面最近的点这样一个概念，这些点实际上就是我们提到过的支持向量。用图像来表示的话可以参考下面的图，图中标红的样本点就是支持向量。

2.最优化问题

 3.对偶性

对于上述不等式约束的凸二次规划问题，我们可以使用拉格朗日乘子法获得其对偶问题。上面的式子可以被重写为如下形式：

拉格朗日乘数法可以将有约束优化转化为无约束优化。假设有一个有约束优化问题：

我们令 则函数 L(x,λ) 被称之为拉格朗日函数，参数 λ 被称为拉格朗日乘子，且λk​≥0。接下来可以通过等式约束的极值必要条件找到可能的极值点：

在等式约束下引入了 l 个拉格朗日乘子，考虑到xi​ 和 λk​ 均为优化变量，此时我们共有 (n+l) 个优化变量。

现在我们将之前获得的不等式写为拉格朗日函数：

4.SVM优化 

现在让我们回到 SVM 的优化上。已知我们的优化目标如下所示：

 现在我们带回到原函数中可得：

对于这种二次规划问题，我们常用 SMO（Sequential Minimal Optimization，序列最小优化）算法求解。该算法的思想就是每次固定其余参数，仅求当前参数的极值。有关于使用 SMO 算法求解在这里我们就不进行推导了，有兴趣的同学可以查阅相关资料。

通过 SMO 算法我们可以算出拉格朗日乘子的最优解 λ∗。接下来我们可以对 L(w,b,λ) 求取偏导数，则 w 的偏导数为：

---

5.软间隔

在真实的生活中，完全线性可分的数据集或者样本是非常少的，而 SVM 的计算过程又严格要求数据集完全线性可分。为了解决这个问题，我们可以加入软间隔来进行缓冲。所谓软间隔就是指允许部分样本点出现在间隔带中。软间隔的情况如下图所示：

可以看到相比于最开始的图，这张图中的间隔带中存在三个样本点，将原本无法完全线性分割的数据集分割开来，这就是软间隔的作用。

为了衡量这个间隔究竟软到何种程度，我们为每个样本引入一个松弛变量 ξi​。令 ξi​=0，且            1-

 在添加软间隔后我们的优化目标就变成了如下形式：

其中 C 是一个大于 0 的常数，通常被称之为惩罚参数，越大越不能容忍错误样本。当 C 趋向无穷大时，ξi​ 必然趋向无穷小，如此我们的优化目标又退化为完全线性可分的情况。等 C 为有限值的时候，才会允许部分样本不遵循约束条件。

现在我们针对新的优化目标求解最优化。首先构造拉格朗日函数：

此时我们可以发现在公式中并不存在松弛变量 ξi​ 的拉格朗日乘子 μi​，因此我们仍然只需要最大化 λ 即可： 

---

6.核函数

在上述过程中，实际上我们只考虑了样本线性可分或者大多数样本线性可分的情况，但是实际上还有很多数据集完全无法被线性分割，例如下图这种情况：

 对这种情况我们可以将线性不可分样本映射到高维空间中，这样我们就可以在高维空间中完成线性分割。以上图为例，我们可以将这个数据集做如下映射：

这样这个数据集就可以在三维空间中被线性分割。像这样在优先维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间中，再通过间隔最大化的方式学习获得支持向量机，这就是非线性 SVM。

然而直接将低维空间映射到高维空间时（尤其是非常高的维度）计算量会非常大，因此我们会通过核函数（kernel function）来进行这种变换。由于在线性 SVM 的对偶问题中，目标函数和分类决策函数都只涉及实例与实例之间的内积，因此我们不需要显式地指定非线性变换，而是用核函数替换其中的内积。核函数的一般形式可以表现为：

由此可见核函数的引入同时降低了计算量和内存使用量。

当我们使用核函数进行非线性分类时，步骤如下：

首先选择适当的核函数和惩罚系数，构造拉格朗日函数并进行求解：

7.优缺点

SVM 的优点包括：

• 严格的数学理论支持，具有很强的可解释性
• 支持向量通常可以理解为关键样本，在某种程度上可以用于数据预处理
• 添加核函数后，可以用于处理非线性分类及回归任务
• 最终决策函数仅由支持向量确定，计算复杂度取决于支持向量的数目而非样本空间维数，在面对高维问题时具有较好的性能

除了优点，SVM 同样具有一些固有问题：

• 训练时间较长。采用 SMO 算法求取拉格朗日乘子时，时间复杂度为O(N2)
• 使用核函数时，如果需要储存核矩阵则空间复杂度将变为O(N2)
• 同样由于决策函数由支持向量决定，当支持向量数量较大时计算复杂度也会迅速上升。因此 SVM 常用于处理小批量样本数据，大规模样本通常不会使用 SVM 进行计算。

---

8.示例代码

在鸢尾花数据集中，目标变量（y）有三种类型，分别用0、1、2表示，具体对应的鸢尾花种类如下：

• 0: 山鸢尾（Iris setosa）
• 1: 变色鸢尾（Iris versicolor）
• 2: 维吉尼亚鸢尾（Iris virginica）

这三种鸢尾花的特征在数据集中有四个属性，包括花瓣长度、花瓣宽度、萼片长度和萼片宽度。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import classification_report# 加载数据
iris = datasets.load_iris()
X = iris.data
y = iris.target# 选取前两个特征用于可视化
X = X[:, :2]# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 数据标准化# StandardScaler(): 创建一个标准化对象。
# fit_transform(): 在训练集上计算平均值和标准差，并应用标准化。
# transform(): 使用在训练集上计算得到的平均值和标准差来标准化测试集。
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)# 创建SVM分类器
svm = SVC(kernel='linear')  # 线性核
svm.fit(X_train, y_train)# 预测和评估
predictions = svm.predict(X_test)
print(classification_report(y_test, predictions))# 绘制分类直线及数据点
# 绘制散点图展示测试集数据的分类情况
plt.scatter(X_test[:, 0], X_test[:, 1], c=predictions, cmap=plt.cm.Set1)# 绘制决策边界线（分类直线）
xx, yy = np.meshgrid(np.arange(X_test[:, 0].min() - 1, X_test[:, 0].max() + 1, 0.02),np.arange(X_test[:, 1].min() - 1, X_test[:, 1].max() + 1, 0.02))
Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], linewidths=1)plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('SVM Classification Result')
plt.show()

---

好的，下面高级玩法。。。 

**Iris 鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）中的哪一品种。

1.数据准备

# 导入相关库
# 导入相关包
import numpy as np#numpy：python第三方库，用于科学计算
import pandas as pd#pandas：提供高性能，易于使用的数据结构和数据分析工具
from pandas import plotting#plotting包是一个Python包，用于绘制各种图形和图表。它提供了一组功能强大的绘图函数和工具，可以快速生成高质量的图形。
from sklearn import datasets#datasets包：文本数据集的处理
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt#plt：plt包是Python中的一个数据可视化库，它的主要功能是绘制各种类型的图表和图形
plt.style.use('seaborn')
import seaborn as sns#sns：提供了一系列高级绘图函数和样式设置，用于创建漂亮的、高效的、统计学模型中必要的图表。
sns.set_style("whitegrid")
from sklearn.linear_model import LogisticRegression #LogisticRegression包是一个Python机器学习库，用于实现逻辑回归算法
from sklearn.model_selection import train_test_split#train_test_split包是用于将数据集分为训练集和测试集的Python库
from sklearn.preprocessing import LabelEncoder#将字符串类型的类别特征转换成数字，以便进行机器学习算法的训练和预测。
from sklearn.neighbors import KNeighborsClassifier#一种基于K近邻算法的分类器，它能够根据给定的训练集中的样本，通过计算测试样本与训练集中每个样本的距离，找到K个离测试样本最近的邻居
from sklearn import svm#支持向量机(SVM)是一种经典的监督机器学习算法，主要用于二分类和多分类问题的分类和回归任务。
from sklearn import metrics #metrics包是Python中用于度量算法性能的包
from sklearn.tree import DecisionTreeClassifier#DecisionTreeClassifier包是一个决策树分类器，用于分类任务#1.数据准备
#*************将字符串转为整型，便于数据加载***********************
def iris_type(s):it = {b'Iris-setosa':0, b'Iris-versicolor':1, b'Iris-virginica':2}return it[s]
#加载数据
data_path=r'C:\pythonProject\机器学习\SVM\iris.data'          #数据文件的路径
data = np.loadtxt(data_path,                                #数据文件路径dtype=float,                              #数据类型delimiter=',',                            #数据分隔符converters={4:iris_type})                 #将第5列使用函数iris_type进行转换
print(len(data))
print()
# 加载数据
data_path = 'C:\pythonProject\机器学习\SVM\iris.data'  # 数据文件的路径
iris = pd.read_csv(data_path, header=None)  # 读数据
iris.columns = ['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm', 'Species']  # 确定列名，参考下面的信息
print(iris.info())
print(iris.describe())
# 设置颜色主题
antV = ['#1890FF', '#2FC25B', '#FACC14', '#223273', '#8543E0', '#13C2C2', '#3436c7', '#F04864']# 绘制  Violinplot
f, axes = plt.subplots(2, 2, figsize=(8, 8), sharex=True)
sns.despine(left=True)
#下面需要连续四句，分别画出横坐标为种类，纵坐标为四个特征的小提琴图sns.violinplot(x='Species', y='SepalLengthCm', data=iris, palette=antV, ax=axes[0, 0])
sns.violinplot(x='Species', y='SepalWidthCm', data=iris, palette=antV, ax=axes[0, 1])
sns.violinplot(x='Species', y='PetalLengthCm', data=iris, palette=antV, ax=axes[1, 0])
sns.violinplot(x='Species', y='PetalWidthCm', data=iris, palette=antV, ax=axes[1, 1])# 设置标题
axes[0, 0].set_title('SepalLengthCm')
axes[0, 1].set_title('SepalWidthCm')
axes[1, 0].set_title('PetalLengthCm')
axes[1, 1].set_title('PetalWidthCm')
plt.show()# 绘制  pointplot
f, axes = plt.subplots(2, 2, figsize=(8, 8), sharex=True)
sns.despine(left=True)
#下面需要连续四句，分别画出横坐标为种类，纵坐标为四个特征的点线图
sns.pointplot(x='Species', y='SepalLengthCm', data=iris, color=antV[0], ax=axes[0, 0])
sns.pointplot(x='Species', y='SepalWidthCm', data=iris, color=antV[1], ax=axes[0, 1])
sns.pointplot(x='Species', y='PetalLengthCm', data=iris, color=antV[2], ax=axes[1, 0])
sns.pointplot(x='Species', y='PetalWidthCm', data=iris, color=antV[3], ax=axes[1, 1])plt.show()#画出四个特征的与类别交汇图，参考约会数据预测中的交汇图
sns.pairplot(iris, hue='Species', palette=antV)
plt.show()#下面分别基于花萼和花瓣做线性回归的可视化：
g = sns.lmplot(data=iris, x='SepalWidthCm', y='SepalLengthCm', palette=antV, hue='Species')
g = sns.lmplot(data=iris, x='PetalWidthCm', y='PetalLengthCm', palette=antV, hue='Species')
plt.show()#最后，通过热图找出数据集中不同特征之间的相关性，高正值或负值表明特征具有高度相关性：
fig=plt.gcf()
fig.set_size_inches(12, 8)
fig=sns.heatmap(iris.corr(), annot=True, cmap='GnBu', linewidths=1, linecolor='k', square=True, mask=False, vmin=-1, vmax=1, cbar_kws={"orientation": "vertical"}, cbar=True)
plt.show()# #接下来，通过机器学习，以花萼和花瓣的尺寸为根据，预测其品种。
#
# 在进行机器学习之前，将数据集拆分为训练和测试数据集。首先，使用标签编码将 3 种鸢尾花的品种名称转换为分类值（0, 1, 2）。# 载入特征和标签集
X = iris[['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm']]
y = iris['Species']# 标签编码
le = LabelEncoder()
y = le.fit_transform(y)
print(y)# 拆分数据集
train_X, test_X, train_y, test_y = train_test_split(X, y,test_size=0.3 , random_state = 101)                               #使用train_test_split对训练集和测试集划分
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)# # 2.SVM分类器
# Support Vector Machine
model = svm.SVC()
model.fit(train_X,train_y)
prediction=model.predict(test_X) #model训练
#model预测
print('The accuracy of the SVM is: {0}'.format(metrics.accuracy_score(prediction,test_y)))# # 3.KNN分类器
# K-Nearest Neighboursmodel=KNeighborsClassifier(n_neighbors=3)model.fit(train_X, train_y)
prediction = model.predict(test_X)#model定义#model训练#model预测print('The accuracy of the KNN is: {0}'.format(metrics.accuracy_score(prediction,test_y)))# # 4.决策树分类器
# Decision Tree
model= DecisionTreeClassifier()
model.fit(train_X,train_y)
prediction=model.predict(test_X)  #model训练#model预测print('The accuracy of the Decision Tree is: {0}'.format(metrics.accuracy_score(prediction,test_y)))# # 5.逻辑回归分类器
# Logistic Regression
model = LogisticRegression()
model.fit(train_X,train_y)
prediction=model.predict(test_X) #model定义#model训练#model预测
print('The accuracy of the Logistic Regression is: {0}'.format(metrics.accuracy_score(prediction,test_y)))
# # 6.模型比较
# 我们可以比较不同模型的准确率，并选择最好的模型。
#只使用花瓣
petal = iris[['PetalLengthCm', 'PetalWidthCm', 'Species']]
train_p,test_p=train_test_split(petal,test_size=0.3,random_state=0)
train_x_p=train_p[['PetalWidthCm','PetalLengthCm']]
train_y_p=train_p.Species
test_x_p=test_p[['PetalWidthCm','PetalLengthCm']]
test_y_p=test_p.Species#只使用花萼sepal = iris[['SepalLengthCm', 'SepalWidthCm', 'Species']]
train_s,test_s=train_test_split(sepal,test_size=0.3,random_state=0)
train_x_s=train_s[['SepalWidthCm','SepalLengthCm']]
train_y_s=train_s.Species
test_x_s=test_s[['SepalWidthCm','SepalLengthCm']]
test_y_s=test_s.Species#SVM分类器
model=svm.SVC()
model.fit(train_x_p,train_y_p)
prediction=model.predict(test_x_p)
print('The accuracy of the SVM using Petals is: {0}'.format(metrics.accuracy_score(prediction,test_y_p)))
model.fit(train_x_s,train_y_s)
prediction=model.predict(test_x_s)
print('The accuracy of the SVM using Sepal is: {0}'.format(metrics.accuracy_score(prediction,test_y_s)))#KNN分类器
model = LogisticRegression()
model.fit(train_x_p, train_y_p)
prediction = model.predict(test_x_p)
print('The accuracy of the Logistic Regression using Petals is: {0}'.format(metrics.accuracy_score(prediction,test_y_p)))
print('The accuracy of the Logistic Regression using Sepals is: {0}'.format(metrics.accuracy_score(prediction,test_y_s)))#决策树分类器
model=DecisionTreeClassifier()
model.fit(train_x_p, train_y_p)
prediction = model.predict(test_x_p)
print('The accuracy of the Decision Tree using Petals is: {0}'.format(metrics.accuracy_score(prediction,test_y_p)))
model.fit(train_x_s, train_y_s)
prediction = model.predict(test_x_s)
print('The accuracy of the Decision Tree using Sepals is: {0}'.format(metrics.accuracy_score(prediction,test_y_s)))#逻辑回归分类器
model=KNeighborsClassifier(n_neighbors=3)
model.fit(train_x_p, train_y_p)
prediction = model.predict(test_x_p)
print('The accuracy of the KNN using Petals is: {0}'.format(metrics.accuracy_score(prediction,test_y_p)))
model.fit(train_x_s, train_y_s)
prediction = model.predict(test_x_s)
print('The accuracy of the KNN using Sepals is: {0}'.format(metrics.accuracy_score(prediction,test_y_s)))