发喷山火(volcano)+CF2119F Volcanic Eruptions 解题报告

发喷山火

神题

先来初步挖掘一下这个走路过程的性质：

1. 初始时 \(S=1\)，且 \(S\le 0\) 就死了，所以在没有走到 \((1,1)\) 之前，只能走 \((1,-1)\) 的边。
2. 由于你和岩浆走路速度相同，所以一旦路径中你已经触碰到岩浆，那么你无论如何都逃不出去了，所以触碰过岩浆等价于最后停下的位置没有岩浆。

由性质1，如果没有经过 \((1,1)\) 的边，那么一定是 \(1,-1,1,-1,\dots\) 交替走。否则先来分析经过 \((1,1)\) 的情况，这显然是强于没有的情况的。

我们试图刻画一下最优走法的形态。往返是不好处理的，我们将在一条边上来回走的行为称为掉头，那么不难发现，在没有经过 \((1,1)\) 之前就掉头一定是不优的，因为我们可以将这些掉头全部放到 \((1,1)\) 的边上不停掉头。

然后就可以将走法刻画成一个简单的形态：一条链外接一条尽头为 \((1,1)\) 边的支链

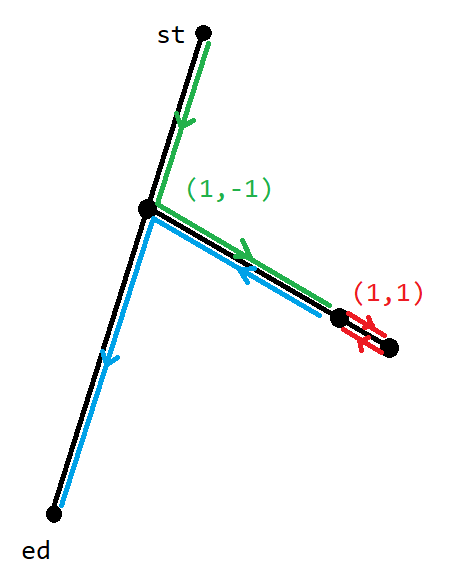
得到形态后，考虑固定住终点 \(ed\)，那么所有满足要求的 \((1,1)\) 就是从主链分出去的各个支链中满足到起点的路径都是 \((1,-1)\) 中最靠近主链的。

接下来考虑表示出答案，记 \(dep_{u}\) 表示根到 \(u\) 的距离。对于一条从 \(st\to ed\) 的路径，其对起点 \(st\) 的贡献是什么？根据前面的分析，没有碰到岩浆等价于最后终点 \(ed\) 没有碰到岩浆，所以到达时间 \(t\le dep_{ed}\)，这样就不用考虑岩浆了，再分析一下取到的上界。注意到走掉头边是不会改变路径长度奇偶性的，原来的简单路径长度奇偶是 \(dep_{st}\oplus dep_{ed}\)，那么奇偶性不会变，有 \(t\equiv dep_{st}\oplus dep_{ed}\pmod 2\)。那么最终的答案可以表示为 \(dep_{ed}-[(dep_{st}\oplus dep_{ed})\not\equiv dep_{ed}\pmod 2]\)，化简为 \(dep_{ed}+(dep_{st}\bmod 2)-1\)。

我们发现，这个答案的式子中只需要对 \(st\) 求出 \(\displaystyle\max_{st\to ed\texttt{ is valid}} dep_{ed}\)。

弱化版(只有一个 \(st\))---CF2119F Volcanic Eruptions：

以 \(st\) 为根，考虑对 \(ed=u\) 处理贡献。用 \(dis_u\) 表示到点 \(u\) 的距离，\(s_u\) 表示到点 \(u\) 的 \(w\) 贡献和。对于一条支链 ，用 \(k\) 表示从主链到最近的 \((1,1)\) 的距离，从这条支链往下走到 \(u\) 的路径最低点为 \(mi\)，设 \(x\) 表示在 \((1,1)\) 上的掉头次数。由于要在 \(dep_{u}\) 时间之前到 \(u\)，所以 \(dis_{u}+2k+2x<dep_u\)，即 \(x\le \left\lfloor\dfrac{dep_u-dis_u-1-2k}{2}\right\rfloor\)，并且要保证走 \(v\to u\) 这条路时生命值始终为正，即 \(mi+2x\ge 1\)，即 \(x\ge \left\lceil\dfrac{-mi+1}{2}\right\rceil\)，只需要 \(x\) 有取值即可，等价于满足：

\[\left\lceil\dfrac{-mi+1}{2}\right\rceil\le \left\lfloor\dfrac{dep_u-dis_u-1-2k}{2}\right\rfloor \\ \Rightarrow \left\lceil\dfrac{-mi+1}{2}\right\rceil\le \left\lfloor\dfrac{dep_u-dis_u-1}{2}\right\rfloor-k \\ \Rightarrow k\le \left\lfloor\dfrac{dep_u-dis_u-1}{2}\right\rfloor-\left\lceil\dfrac{-mi+1}{2}\right\rceil \]

于是可以在 \(\mathrm{dfs}\) 的过程中维护上述信息，时间复杂度 \(O(n)\)。