[数据结构——lesson10.2堆排序以及TopK障碍]

目录

前言

学习目标

堆排序

TopK问题：

解法一：建立N个数的堆

解法二：建立K个数的堆（最优解）

完整代码

结束语

---

前言

上节内容我们详细讲解了堆[数据结构——lesson10.堆及堆的调整算法]，接下来我们来讲解堆的一个经典应用——TopK问题。

学习目标

• 堆排序
• 掌握堆的应用理解TopK问题

两种调整算法的复杂度精准剖析

开头讲了两种堆的调整算法，分别是【向上调整】和【向下调整】，在接口算法实现Push和Pop的时候又用到了它们，以及在建堆这一块我也对它们分别做了一个分析，所以我们本文的核心就是围绕这两个调整算法来的，但是它们两个到底谁更加优一些呢❓
这里就不做过多解释，直接看图即可

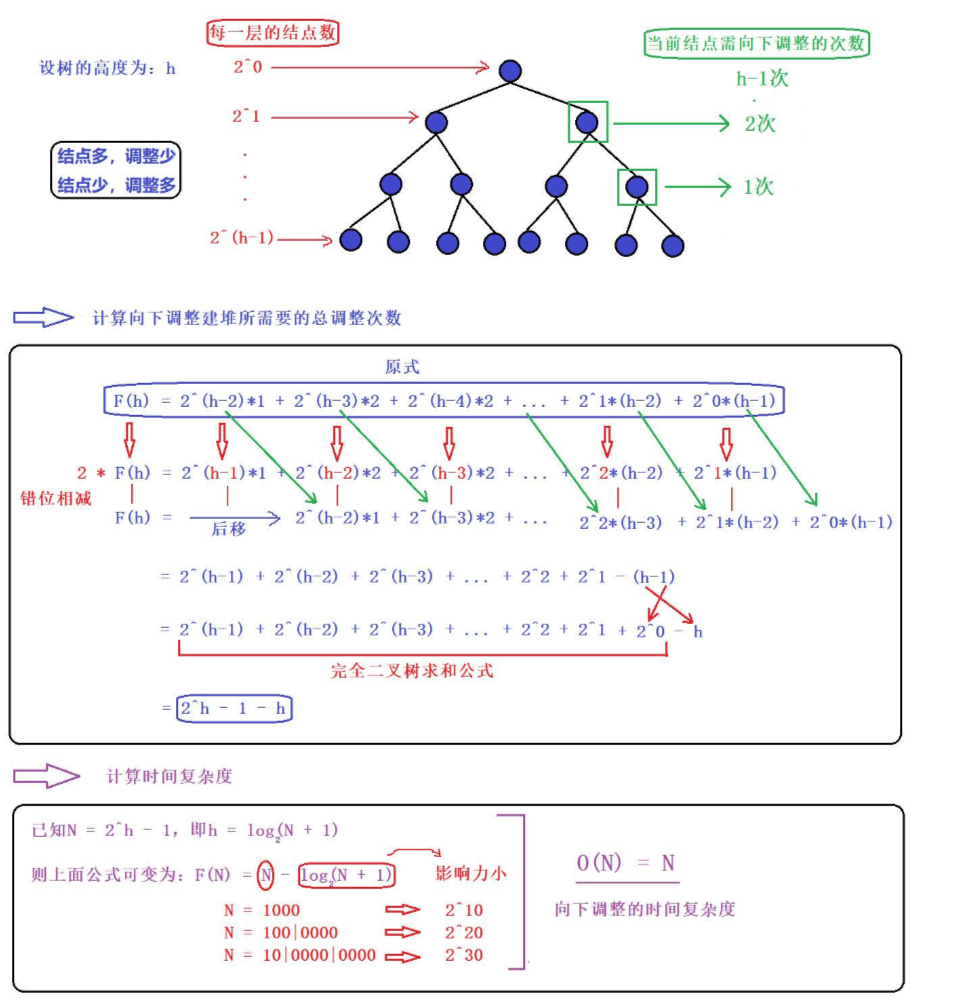
1、向下调整算法【重点掌握】

2、向上调整算法

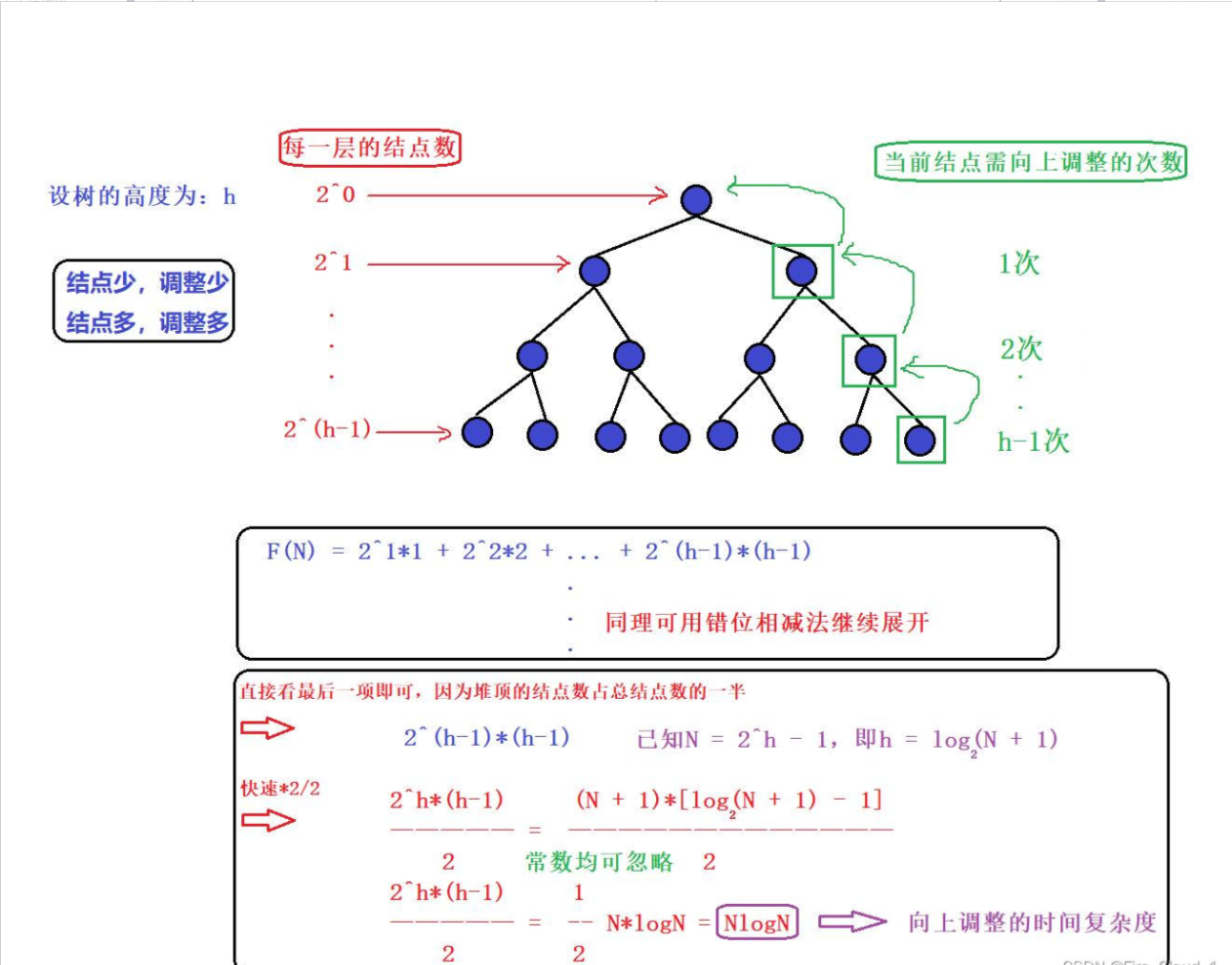
好，我们来总结一下，【向上调整算法】，它的时间复杂度为O(NlogN)；【向下调整算法】，它的时间复杂度为O(N)
很明显，【向下调整算法】来得更优一些，因为向下调整随着堆的层数增加结点数也会变多，可是结点越多调整得就越少，因为在一些大型数据处理场合我们会使用向下调整
当然在下面要讲的堆排序中我们建堆也是利用的向下调整算法，所以大家重点掌握一个就行

堆排序

讲了那么久的堆，学习了两种调整算法以及它们的时间复杂度分析，接下去我们来说说一种基于堆的排序算法——【堆排序】

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1. 建堆

• 升序：建大堆
• 降序：建小堆

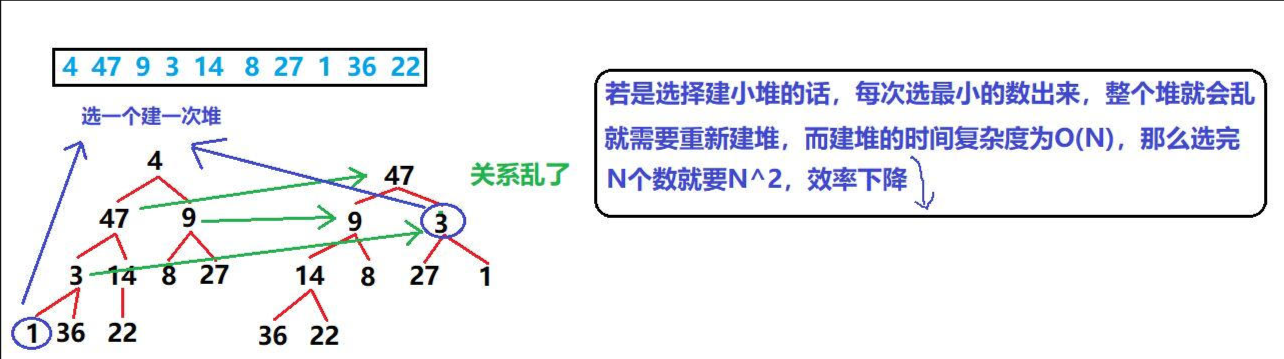
这里我们以升序为例（升序建大堆 or 小堆❓）

• 在上面解说的时候，我建立的默认都是大堆，但是在这里我们要考虑排序问题了，现在面临的是【升序】，对于升序就是数组前面的元素小，后面的元素大，这个堆也是基于数组建立的，那就是要堆顶小，堆顶大,很明显就是建【小堆】
• 一波分析猛如虎，我们通过画图来分析是否可以建【小堆】

• 可以看到，对于建小堆来说，原本的左孩子结点就会变成新的根结点，而右孩子结点就会变成新的左孩子结点，整个堆会乱，而且效率并不是很高，因此我们应该反一下，去建大堆

//建立大根堆（倒数第一个非叶子结点）
for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i)
{
Adjust_Down(a, n, i);
}

所以应建大堆。

堆排序的基本思路是每次将堆顶元素取出放到有序区间。大堆（大顶堆）中每个节点的值都大于或等于其子节点的值，堆顶元素为最大值。升序排序时建大堆，可将堆顶的最大值与无序区间最后一个数交换，使有序区间增加一个最大值。然后对剩余元素重新调整堆结构，重复此过程，就能逐渐将序列变为升序。

若升序建小堆，虽然堆顶是最小值，但确定次小值时会很麻烦，因为次小值可能是堆顶的左孩子或右孩子，甚至需要重新建堆，导致排序效率降低。

如何进一步实现排序❓

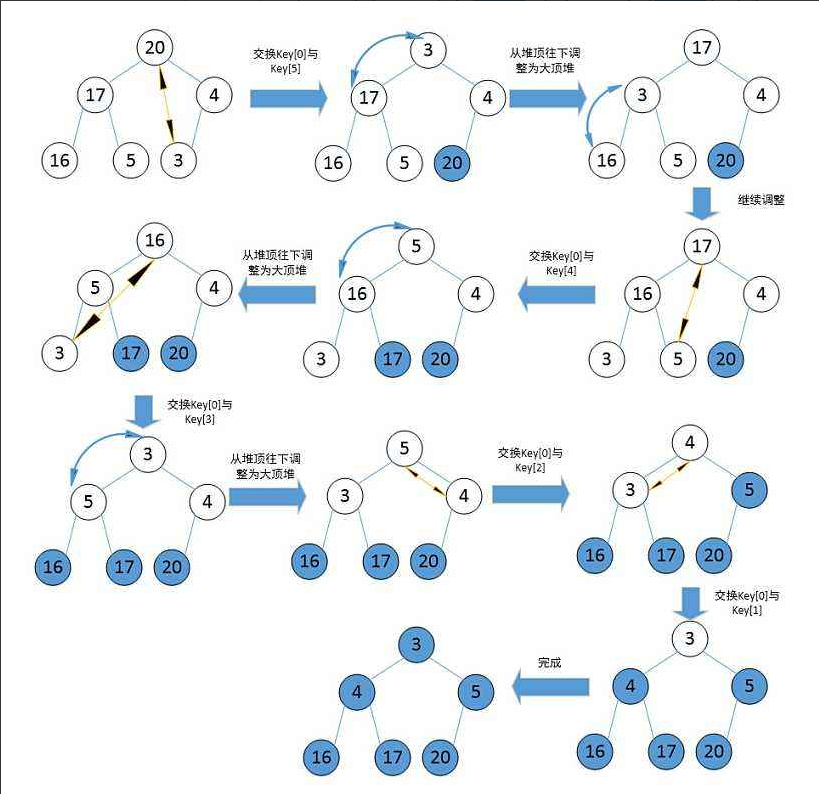
• 有了一个大堆之后，如何去进一步实现升序呢，这里就要使用到在Pop堆顶数据的思路了，也就是现将堆顶数据与堆底末梢数据做一个交换，然后对这个堆顶数据进行一个向下调整，将大的数往上调。具体过程如下

2. 利用堆删除思想来进行排序

建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

• 对照代码，好好分析一下堆排的全过程吧

/*堆排序*/
void HeapSort(int* a, int n)
{
//建立大根堆（倒数第一个非叶子结点）
for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i)
{
Adjust_Down(a, n, i);
}
int end = n - 1;
while (end > 0)
{
swap(&a[0], &a[end]);		//首先交换堆顶结点和堆底末梢结点
Adjust_Down(a, end, 0);		//一一向前调整
end--;
}
}

• 看一下时间复杂度，建堆这一块是O(N)，调整这一块的话就是每次够把当前堆中最的数放到堆底来，然后每一个次大的数都需要向下调整O(log2N)，数组中有N个数需要调整做排序，因而就是O(Nlog2N)。
• 当然你可以这么去看：第一次放最大的数，第二次是次大的数，这其实和我们上面讲过的向上调整差不多了，【结点越少，调整越少；结点越多，调整越多】，因此它也可以使用之前我们分析过的使用的【错位相减法】去进行求解，算出来也是一个O(Nlog2N)。
• 最后将两段代码整合一下，就是O(N + Nlog2N)，取影响结果大的那一个就是O(Nlog2N)，这也就是堆排序最终的时间复杂度

---

TopK问题：

Top-K 问题是一类常见的算法和数据处理问题，指从包含 N 个元素的大量数据集合中找到前 K 个最大或最小的元素，通常 N 远大于 K。

Top-k问题在生活中是非常的常见，比如游戏中某个大区某个英雄熟练度最高的前10个玩家的排名，我们就要根据每个玩家对该英雄的熟练度进行排序，可能有200万个玩家，但我只想选出前10个，要对所有人去排个序吗？显然没这个必要。

再比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

• 问题特点：数据量 N 极大时，若直接对所有数据排序（如快排，时间复杂度为 O (n log n)），不仅耗时久，还可能需将所有数据加载到内存，空间成本极高。而 K 通常很小，只需关注 “最大或最小的前 K 个”，无需对所有数据排序，因此需要更高效的算法来解决。

---

解法一：建立N个数的堆

建一个 N 个数的堆（C++中可用优先级队列priority_queue），不断的选数，选出前 k 个。

时间复杂度：建N个数的堆为O(N)，获取堆顶元素 (也即是最值) 并删除掉堆顶元素为O(log2N)，上述操作重复 k 次，所以时间复杂度为O(N+k*log2N)。

【思考】

但是这样也会存在上述所讲的可能需将所有数据加载到内存，空间成本极高的问题，能否再优化一下呢？

---

解法二：建立K个数的堆（最优解）

解决思路（堆排序）

• 若要找前 K 个最大的元素，则建立小顶堆；
• 若要找前 K 个最小的元素，则建立大顶堆。
• 首先用数据集合中前 K 个元素来建堆，然后将剩余的 N-K 个元素依次与堆顶元素比较；
• 若大于（针对小顶堆）或小于（针对大顶堆）堆顶元素，则替换堆顶元素并重新调整堆；
• 遍历完剩余元素后，堆中的 K 个元素就是所求的前 K 个最大或最小的元素。

时间复杂度：

▶ 建 k 个元素的堆为O(K)；
▶ 遍历剩余的 N-K 个元素的时间代价为O(N-K)，假设运气很差，每次遍历都入堆调整；
▶ 入堆调整：删除堆顶元素和插入元素都为O(log2K)；
▶ 所以时间复杂度为O(k + (N-K)log2K)。当 N 远大于 K 时，为O(N*log2K)，这种解法更优。

假如要找出最大的前 10 个数：

▶ 建立 10 个元素的小堆，数据集合中前 10 个元素依次放入小堆，此时的堆顶元素是堆中最小的元素，也是堆里面第 10 个最小的元素，
▶  然后把数据集合中剩下的元素与堆顶比较，若大于堆顶则去掉堆顶，再将其插入，
▶  这样一来，堆里面存放的就是数据集合中的前 10 个最大元素，
此时小堆的堆顶元素也就是堆中的第 10 个最大的元素

思考：为什么找出最大的前10个数，不能建大堆呢？

• 找出最大的前 10 个数不能建大堆，原因在于大堆的特性会导致只能找到最大的数，而无法找到其余较大的数。
• 大堆的性质是堆顶元素为堆中最大的元素。当使用 10 个元素建大堆时，堆顶就是这 10 个元素中最大的，若数据集合中还有其他更大的数，由于它们都小于当前堆顶元素，根据大堆的插入规则，这些数无法进入堆中。所以最终只能得到最大的那个数，无法找出前 10 个最大的数。
• 相反，若建立小堆，堆顶是堆中最小的元素，当有比堆顶大的元素出现时，就可以替换堆顶元素，并通过调整堆结构使小堆性质得以维持，这样就能保证较大的数逐渐进入堆中，最终堆中的 10 个元素就是数据集合中前 10 个最大的数。

完整代码

以从1w个数里找出最大的前10个数为例：

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
// 大堆调整
void max_heapify(int* arr, int i, int size)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left  arr[largest])
largest = left;
if (right  arr[largest])
largest = right;
if (largest != i)
{
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
max_heapify(arr, largest, size);
}
}
// 构建大根堆
void build_max_heap(int* arr, int size)
{
for (int i = size / 2 - 1; i >= 0; i--)
max_heapify(arr, i, size);
}
// 堆排序
void heap_sort(int* arr, int size)
{
build_max_heap(arr, size);
for (int i = size - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
max_heapify(arr, 0, i);
}
}
// 获取前k个最小元素
void get_topk_smallest(int* arr, int n, int k, int* result)
{
if (k > n) k = n;
int* heap = (int*)malloc(k * sizeof(int));
if (heap == NULL) {
printf("内存分配失败\n");
return;
}
// 取前k个元素构建大堆
for (int i = 0; i < k; i++)
heap[i] = arr[i];
build_max_heap(heap, k);
// 遍历剩余元素
for (int i = k; i < n; i++)
{
if (arr[i] < heap[0])
{
heap[0] = arr[i];
max_heapify(heap, 0, k);
}
}
// 排序结果并输出
heap_sort(heap, k);
for (int i = 0; i < k; i++)
result[i] = heap[i];
free(heap);
}
// 生成随机数组
void generate_random_array(int* arr, int size, int min, int max)
{
srand(time(NULL));
for (int i = 0; i < size; i++)
{
arr[i] = min + rand() % (max - min + 1);
}
}
// 打印数组
void print_array(int* arr, int size)
{
for (int i = 0; i < size; i++)
{
printf("%d ", arr[i]);
if ((i + 1) % 10 == 0)
printf("\n");
}
printf("\n");
}
// 验证结果正确性（通过全排序对比）
void verify_result(int* arr, int n, int k, int* topk)
{
// 创建数组副本并排序
int* copy = (int*)malloc(n * sizeof(int));
for (int i = 0; i < n; i++)
copy[i] = arr[i];
heap_sort(copy, n);  // 注意：这里堆排序是升序
printf("\n验证结果（前10个最小元素）：\n");
printf("算法结果：");
for (int i = 0; i < k; i++)
printf("%d ", topk[i]);
printf("\n正确结果：");
for (int i = 0; i < k; i++)
printf("%d ", copy[i]);
printf("\n");
// 检查是否一致
int correct = 1;
for (int i = 0; i < k; i++)
{
if (topk[i] != copy[i])
{
correct = 0;
break;
}
}
printf("验证结果：%s\n", correct ? "正确" : "错误");
free(copy);
}
int main()
{
const int N = 10000;  // 数据总量
const int K = 10;     // 要找的最小元素个数
int* arr = (int*)malloc(N * sizeof(int));
int* topk = (int*)malloc(K * sizeof(int));
// 生成10000个1到100000之间的随机数
generate_random_array(arr, N, 1, 100000);
printf("已生成10000个随机数\n");
// 计算前10个最小元素
clock_t start = clock();
get_topk_smallest(arr, N, K, topk);
clock_t end = clock();
// 输出结果
printf("\n最小的前10个数（升序排列）：\n");
print_array(topk, K);
// 输出耗时
double time_spent = (double)(end - start) / CLOCKS_PER_SEC;
printf("计算耗时：%.6f秒\n", time_spent);
// 验证结果
verify_result(arr, N, K, topk);
// 释放内存
free(arr);
free(topk);
return 0;
}

运行结果：

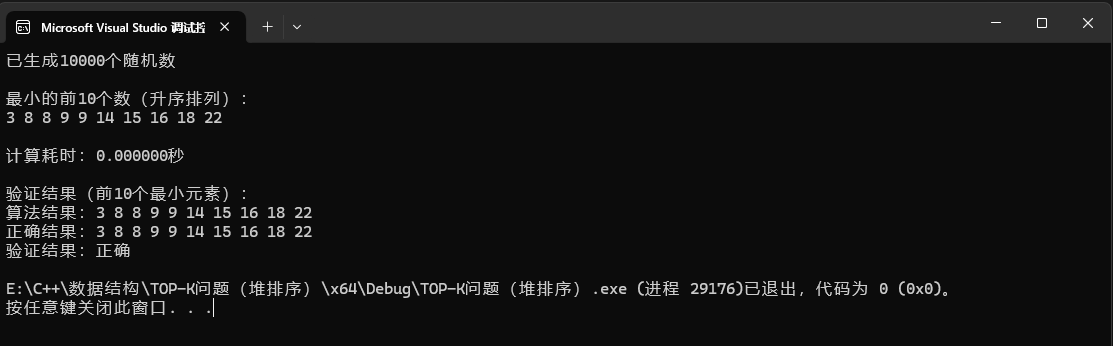
结束语

经过上节堆的学习，这一节我们对于堆的Top K问题的学习与理解相对会轻松很多。

感谢您的三连支持！！！