发现自己阅读量最高的 wqs二分 有点简略,而且有些地方是错的,所以就重构了一下,并加入了更多的例题。
前面基本上都是照搬的原来那篇文章。
介绍
wqs 二分最初由王钦石在他的 2012 年国家集训队论文中提出,也叫"带权二分",或者"dp凸优化",而从 IOI 2016 的 Aliens 题目开始,这种方法开始逐步在竞赛圈中有了一定的地位。在国内我们一般称为「wqs 二分」,而在国外一般称为「Alien Trick」。
特征
wqs 二分的题目一般有以下特点:
- 题目内容形式为:有 \(n\) 个物品,从中选出 \(m\) 个,要求最后的权值最小/最大。
- 直接 DP 设 \(f_{i,j}\) 表示前 \(i\) 个选出 \(j\) 个物品的话,时间复杂度无论如何都是 \(O(n^2)\) 及以上的。
- 如果没有选 \(m\) 这个限制,那可以优化到更低复杂度,并且可以算出此时最优方案选的数的个数。
- 答案关于选的物品个数具有凸性,即如果设 \(g(x)\) 表示选 \(x\) 个物品可以得到的最小/最大权值,那么 \(g(x)\) 的图像构成一个凸包。
当然 wqs 二分不止应用于 DP 题,具体看例题。
算法
大致流程
假设 \(g(x)\) 的图像为上凸包,此时我们要求最大值,不妨画一下 \(g(x)\) 的大致图像(当然其实我们是一个点都求不出来的):
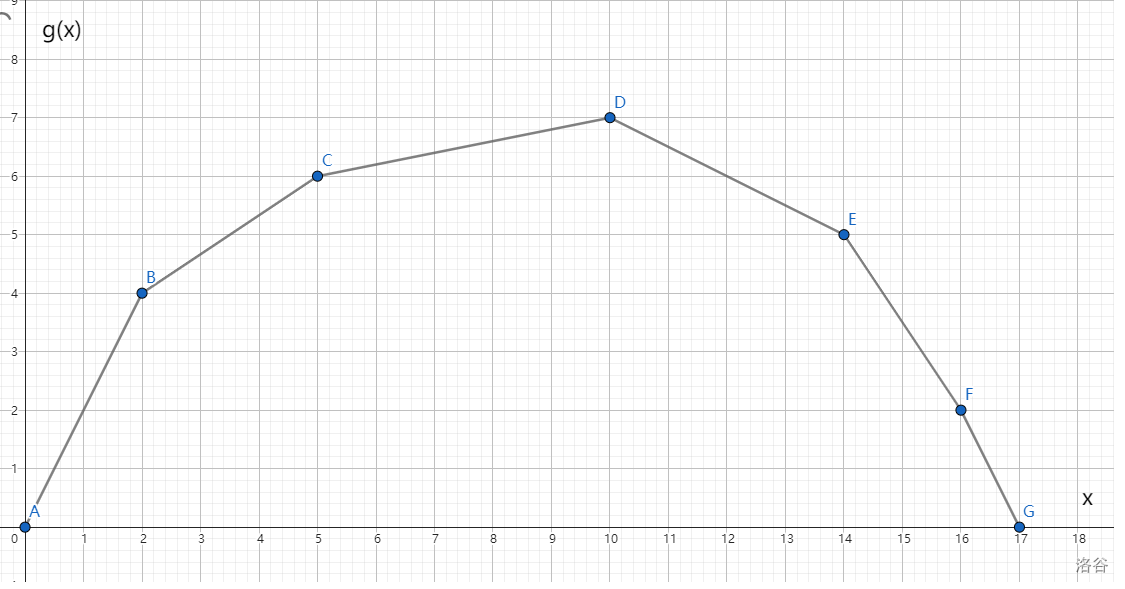
假设我们现在用一条直线 \(y=kx+b\) 去切一个点 \((x,g(x))\),那么可以得到 \(g(x)=kx+b\),即这个点的坐标也可以表示成 \((x,kx+b)\)。
又因为上凸包有个性质,一条斜率为 \(k\) 的直线在他与这个凸包的切点处截距最大,也就是说如果我们能求出这个最大截距,并知道此时的横坐标,就能知道那个切点的具体坐标了。
因为凸包的斜率是单调的,所以随着 \(k\) 的减小,切到的 \(x\) 也越大,所以可以二分这个 \(k\),然后根据切点的坐标去调整 \(k\) 直到切到 \((m,g(m))\) 为止。
现在的问题就是怎么求最大截距,因为我们压根不知道这个凸包长什么样子。
会发现 \(b = g(x)-kx\),定义 \(h(x) = g(x)-kx\),如果我们能以较低的复杂度求出最大的 \(h(x)\) 以及此时的 \(x\),也就求出了我们要的东西。
考虑给 \(h(x)\) 定义一个合理的意义,不难发现他其实就是给每个物品多加了一个 \(-k\) 的权值,选了这个物品就要 \(-k\)。
而我们要求 \(h(x)\) 的最大值是没有限制要选多少个的,所以 DP 时只需要设一维即可,会更好求,具体的优化方法/求法因题目而异,在例题中会讲。
注意最后求 \(g(x)\) 时,要记得把 \(kx\) 加上。
实现细节——共线情形
当凸包上存在多个点共线的时候,我们二分的直线可能会同时切到很多点,如果我们最后求出来的 \((x,h(x))\) 是从中任取一个的话,会使得我们可能漏掉最终答案的位置。因此我们需要保证每次求出来的切点是所有可行切点中横坐标最小/最大的。以上凸壳为例,如果我们每次求出来的 \(x\) 是最小的,那么二分应该写的是 if(x<=mid) r=mid-1,更新答案; else l=mid+1;否则如果我们求出来的 \(x\) 是最大的,那么二分应该写的是 if(x>=mid) l=mid+1,更新答案; else r=mid-1。
这是 wqs 二分最容易出错的点,在之后的例题中也会额外注明。
常见误区
- 由于相邻两点的横坐标之差是 \(1\),所以此时斜率和差分没有区别,而当 \(g(x)\) 一定是整数时,斜率也一定是整数,因此我们二分也只需要二分整数域就一定可以切到要求的点;而当最后的答案可能是小数时,我们二分的斜率也应是实数域。
- 假设我们最终二分出来的斜率为 \(k\),在
check函数里求出来的是 \((x,h(x))\),那么假设我们在共线的时候取的是 \(x\) 最小的,则我们只能保证 \(x\le m\),即 \(x\) 不一定恰好就是 \(m\),但是我们可以知道用斜率为 \(k\) 的线去切,切在 \(x\) 上和切在 \(m\) 上的截距都是 \(h(x)\),因此最后的答案是 \(h(x)+km\),而不是 \(h(x)+kx\)。
凸性证明
显然 wqs 二分最难的部分在于凸性的证明,其他部分都是套路和板子,以下是常见证明凸性的方法:
- 感性理解/打表验证:很多时候在比赛时我们无法或者没有时间证明一个东西的凸性,此时常见的思路是猜测他具有凸性,之后通过感性理解/打表验证的方式非严谨地证明他的凸性。如例题 I。
- 规约为费用流等凸的问题。如例题 III。
- 通过 DP 转移方程归纳证明凸性。
- 交换论证:以最小化问题为例,假设我们现在有了 \(g(x)\) 和 \(g(x+2)\) 的方案构造,此时我们通过交换其中的元素构造出了两个 \(x+1\) 的方案,那么就证明了 \(2g(x+1)\le g(x)+g(x+2)\) 即 \(g(x+1)-g(x)\le g(x+2)-g(x+1)\),所以函数是下凸的。如例题 IV。
- 四边形不等式:对于带个数限制的区间分拆问题,朴素 DP 是 \(f(i,j)\) 表示前 \(i\) 个元素划分为 \(j\) 段的答案,转移为 \(f(i,j)=\min_{k<i}(f(k,j-1)+w(k+1,i))\),若代价函数 \(w(l,r)\) 满足四边形不等式,则 \(g(x)=f(n,x)\) 为关于 \(x\) 的下凸函数。证明见 oi-wiki 该页面。如例题 II。
例题
I. [国家集训队] Tree I
典中典。
恰好 \(need\) 条边考虑 wqs 二分,发现最小生成树的边权和关于白边数量是下凸的,所以直接 wqs 即可,check 函数只需要把每条白边的权值 \(-mid\) 然后跑 Kruskal。
共线情形的处理:我们要保证权值和相同的生成树求出来的是白边数量最小的,只需要 Kruskal 排序的时候把相同权值的黑边放白边前面即可。
凸性证明:我暂时还没有找到我能看懂又严谨的证明方法,所以这里给一下感性理解:考虑从初始最小生成树变到有 \(k\) 条白边的最小生成树的过程。我们每次都是选择一条白边(\(w_1\)),替换掉他的两端的树上路径上的最大黑边(\(w_2\)),并使边权之差 \(w_1-w_2\) 最小(如果初始最小生成树的白边数量大于 k 的话,那就是每次选一条黑边替换白边) 。如果在第 \(i\) 次替换后的增加量 \(>\) 第 \(i+1\) 次替换后的增加量,我们可以交换这两次替换。因此最小生成树的边权和是关于白边数量下凸的。
点击查看代码
int n,m,k,tot,cnt,MST,fa[N];
struct Edge{int u,v,w,col;
}E[M];
int get(int x){return (x==fa[x])?x:(fa[x]=get(fa[x]));}
int val(Edge x,int mid){if(x.col) return x.w;return x.w-mid;
}
int check(int mid){sort(E+1,E+m+1,[&](Edge x,Edge y){if(val(x,mid)==val(y,mid)) return x.col>y.col;return val(x,mid)<val(y,mid);});MST=cnt=0;for(int i=0;i<n;i++) fa[i]=i;for(int i=1;i<=m;i++){int u=E[i].u,v=E[i].v,w=val(E[i],mid),col=E[i].col;if(get(u)==get(v)) continue;fa[get(u)]=get(v);MST+=w,cnt+=1-col;}return cnt;
}
signed main(){n=read(),m=read(),k=read();for(int i=1;i<=m;i++){int u=read(),v=read(),w=read(),col=read();E[i]={u,v,w,col};}int l=-100,r=100,mid,res;while(l<=r){mid=(l+r)>>1;if(check(mid)<=k) res=mid,l=mid+1;else r=mid-1;}check(res);printf("%d\n",MST+k*res);return 0;
}
II. 忘情
把式子变成 $((\sum_{i=1}^n x_i)+1)^2 $,设 \(S\) 为前缀和,那么朴素的 DP 是:
设 \(f_{i,j}\) 表示前 \(i\) 个数划分成 \(j\) 段的最小值,转移为 \(f_{i,j}=\min_{0\le k<i}(f_{k,j-1} + (S_i - S_k + 1)^2)\)。
恰好 \(m\) 段考虑 wqs 二分,发现答案关于划分段数是下凸的。check 时一段的权值定义为 \(((\sum x_i)+1)^2 - K\),然后去掉段数限制,求最小答案。
考虑对这个新的问题 DP,设 \(dp_i\) 表示前 \(i\) 个数的最小值,\(dp_i=\min_{0\le j<i}(dp_j + (S_i-S_j+1)^2 - K)\),注意还需要记录当前分了多少段。
这是经典的斜率优化形式,可以用单调队列优化到 \(O(n)\),不会斜率优化的戳这里。
总时间复杂度 \(O(n \log n)\)。
共线情形处理:显然下标越小最优情况下分的段数也越少,所以斜率优化时对于斜率相同的段我们选择保留而非弹出队列即可取到最小的转移点。(也可以看代码中的注释)
凸性证明:不难验证 \(w(l,r)=(S_r-S_{l-1}+1)^2\) 满足四边形不等式,所以是凸的。
当然也有感性理解:注意到
\((a+b+1)^2=a^2+b^2+1+2ab+2a+2b\)
\((a+1)^2+(b+1)^2=a^2+2a+b^2+2b+2\)
因此把一段拆成两段可以减少 \(2ab-1\)。
而段数越多 \(a,b\) 越小,所以随着 \(m\) 的增加 \(g(m)\) 的值减小的幅度越来越小,函数下凸。
点击查看代码
int n,m,a[N],dp[N],g[N],dq[N],l,r;
int calc(int j){ return dp[j]+a[j]*a[j]-2ll*a[j];
}
void check(int mid){l=1,r=0;dp[0]=0,g[0]=0; dq[++r]=0; for(int i=1;i<=n;i++){while(l<r && ( calc(dq[l+1]) - calc(dq[l]) ) < (2ll * a[i] * (a[dq[l+1]] - a[dq[l]]))) l++; int j=dq[l];dp[i]=dp[j]+(a[i]-a[j]+1ll)*(a[i]-a[j]+1ll)+mid;g[i]=g[j]+1ll;while(l<r && ( calc(i) - calc(dq[r]) ) * ( a[dq[r]] - a[dq[r-1]]) < ( calc(dq[r]) - calc(dq[r-1] ) ) * ( a[i] - a[dq[r]] )) r--;
//这里写 < 就是取最靠左的点;<= 就是取最靠右的点dq[++r]=i; }
}
signed main(){n=read(),m=read();for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];int l=0,r=inf,mid,ans=0; //注意实际上斜率是负的,这里改成正的了,所以 check 函数内部是 +midwhile(l<=r){mid=(l+r)>>1;check(mid);if(g[n]<=m) r=mid-1,ans=mid;else l=mid+1; }check(ans);printf("%lld\n",dp[n]-ans*m);return 0;
}
III. CF739E Gosha is hunting
这个题存在二维 wqs 二分的写法,但是我不会,具体见 严谨的 wqs 二分 或 oi-wiki。但是,洛谷早期题解区的二维 wqs 二分全是错的(貌似目前还剩一篇),原因下面会有,注意区分。
不难列出期望 DP:\(f_{i,j,k}\) 表示前 \(i\) 个神奇宝贝,用 \(j\) 个宝贝球,\(k\) 个超级球的期望。
由于同时用两个球的概率 \(p+u-pu\) 一定 \(\ge p,u\) 所以全用了一定不劣,所以答案是 \(f_{n,a,b}\)。
复杂度 \(O(n^3)\)。
然后是发现 \(f_{n,a,i}\) 是关于 \(i\) 的上凸函数,感性理解不难,严谨证明如下。
考虑建费用流(\((w,c)\) 表示一条边的容量为 \(w\),费用为 \(c\)):
- 建立两个点 \(x,y\) 来限制选球的个数: \(S\to x (a,0)\) ,\(S\to y (b,0)\)。
- \(x\to i (1,p_i)\)。
- \(y\to i (1,u_i)\)。
- \(i\to T\):连两条边,一条 \((1,0)\) 一条 \((1,-p_iu_i)\),由于 \(-p_iu_i\le 0\) 所以保证了在 \(i\) 的入流 \(= 1\) 时会优先走费用为 \(0\) 的边。
最大费用最大流即为答案,根据费用流可证明在一维确定时,另一维有凸性。
费用流的凸性是从整体上的流量和费用来说的,所以无法证明两维同时具有凸性,这也是洛谷早期题解二维 wqs 二分错的原因。
所以可以 wqs 二分,每选一个超级球就要带上 \(-k\) 的代价,\(O(n^2)\) DP 出最优情况选的超级球的个数,直到这个个数 \(=b\),复杂度 \(O(n^2 \log n)\)。
然后发现对于一个神奇宝贝 \(i\) 的四种情况:
- 只选宝贝球:\(p\)
- 只选超级球:\(u-k\)
- 同时选:\(p+u-pu-k\)
- 不选:\(0\)
由于宝贝球的最终使用个数是确定的(一定是 \(a\) 个),所以我们可以一开始钦定不用宝贝球。
那么一个神奇宝贝从不用宝贝球,到用宝贝球,增加量 \(\Delta=max(p,p+u-pu-k)-max(u-k,0)\)。
由于 \(p\ge 0,p+u-pu-k\ge u-k\) 所以 \(\Delta\ge 0\)。
于是我们按照 \(\Delta\) 排序,选最大的那 \(a\) 个使用宝贝球即可。
\(O(n\log^2 n)\),其实不难做到 \(O(n\log n)\)。
共线情形处理不难,注意要实数域二分。
点击查看代码
int n,a,b;
double p[N],u[N],ans;
struct P{double deta;bool fl0,fl1;
}A[N];
bool check(double k){ans=0;int cnt=0;for(int i=1;i<=n;i++){if(p[i]+u[i]-p[i]*u[i]-k>p[i]) A[i].deta=p[i]+u[i]-p[i]*u[i]-k,A[i].fl1=true;else A[i].deta=p[i],A[i].fl1=false;if(u[i]-k>0) A[i].deta-=u[i]-k,A[i].fl0=true,ans+=u[i]-k;else A[i].deta-=0,A[i].fl0=false;} sort(A+1,A+n+1,[&](P x,P y){return x.deta>y.deta;});for(int i=1;i<=a;i++) ans+=A[i].deta,cnt+=A[i].fl1;for(int i=a+1;i<=n;i++) cnt+=A[i].fl0;return cnt<=b;
}
signed main(){ios::sync_with_stdio(false);cin.tie(0);cin>>n>>a>>b;for(int i=1;i<=n;i++) cin>>p[i];for(int i=1;i<=n;i++) cin>>u[i];double l=0,r=1,mid;while(r-l>eps){mid=(l+r)/2.0;if(check(mid)) r=mid;else l=mid;}printf("%.6lf\n",ans+l*b); return 0;
}
IV. [ARC168E] Subsegments with Large Sums
看到恰好 \(k\) 段起手 wqs 二分但是他没有凸性。
考虑先去掉这 \(k\) 段拼起来一定要是原序列的限制,我们称一个子段合法当且仅当元素之和 \(\ge S\)。
如果我们划分出了 \(x\) 段不相交的合法段,设他们的长度之和为 \(len\),则我们根据这 \(x\) 段可以去生成原问题的划分方案,且划分的段数的取值范围为 \([x,x+n-len]\)。
所以合法当且仅当 \(x\le k\le x+n-len\),即 \(x\le k,len-x\le n-k\)。
我们定义一个段的权值为 \(r-l\),设 \(f(x)\) 表示划分出 \(x\) 段不相交的合法段,每一段的权值和的最小值。
则 \(x\) 可行相当于 \(x\le k,f(x)\le n-k\),我们要求的答案就是最大的 \(x\)。
接下来我们证明 \(f(x)\) 是一个下凸函数,证明来自官方题解。
首先 \(f(x)\) 是单增函数是显然的。
我们找出原序列中所有极短合法的子段,假设有 \(m\) 个,因为极短,所以不存在包含关系,所以我们按照左端点排序,右端点自然升序,我们顺次给他们编号 \(1,2,...,m\)。
不难证明 \(f(x)\) 对应的那些段一定包含于这 \(m\) 段。
对于 \(f(p)\) 和 \(f(p+2)\),我们设 \(x_1\le x_2\le \dots \le x_p\) 为 \(f(p)\) 对应的那些段的编号,同理设 \(y_1\le y_2\le \dots \le y_{p+2}\) 为 \(f(p+2)\) 对应的那些段的编号。
特殊的,我们规定 \(x_0=y_0=0,x_{p+1}=y_{p+3}=m+1\)。
并且根据 \(f\) 的要求,第 \(x_i\) 段和第 \(x_{i+1}\) 是不相交的(\(y\) 同理)。
如果我们能找到一个 \(i (0\le i\le p)\) 满足 \(x_i\le y_{i+1}<y_{i+2}\le x_{i+1}\),那么我们可以构造出如下两个合法的 \(p+1\) 的方案:
- \(x_1,x_2,\dots , x_i,y_{i+2},\dots , y_{p+2}\)
- \(y_1,y_2,\dots , y_{i+1},x_{i+1},\dots , x_p\)
因为 \(y_{i+1}\ge x_i\) 而 \(y_{i+2}\) 和 \(y_{i+1}\) 不交,所以 \(y_{i+2}\) 也必定和 \(x_i\) 不交,同理 \(x_{i+1}\) 也必定和 \(y_{i+1}\) 不交,所以这两个方案是合法的。
因此 \(2f(i+1)\le f(i)+f(i+2)\)。
然后就是证明为什么一定存在这样的 \(i\)。
这个其实都不需要"第 \(x_i\) 段和第 \(x_{i+1}\) 是不相交的"这个限制,相当于一个数轴上除了两个端点 \(0,m+1\) 外中间还有 \(p\) 个关键点。然后你需要往上放 \(p+2\) 个点,不难发现如果不存在这样的 \(i\) 的话你最多只能往上放 \(p+1\) 个点。所以这样的 \(i\) 是一定存在的。
wqs 二分的内层 DP 是个简单的前缀 \(\min\) 优化。
最后是这题特殊的细节,这个 wqs 要求的是满足某个限制的 \(x\) 的最大值,而非某个给定的 \(x\)。
所以当我们最后的斜率 \(k\) 切到一个斜率相同的区间时,由于最后的答案可能是某个中间的点,无法直接算出 \(x\)。
我们可以先求出满足切到的区间的左端点合法的最大的 \(k\),此时右端点一定不合法,而这一段的斜率已经知道了,所以可以 \(O(1)\) 递推出下一项的 \(f\) 值。不断往后跳直到不合法就结束即可。
点击查看代码
int n,k,S,a[N];
PII f[N],pre[N];
bool check(int mid){f[0]={0,0},pre[0]={-1,0};for(int l=0,r=1;r<=n;r++){while(a[r]-a[l+1]>=S) l++;f[r]=f[r-1];if(a[r]-a[l]>=S) f[r]=min(f[r],mk(pre[l].fi+r-mid,pre[l].se+1));pre[r]=min(pre[r-1],{f[r].fi-(r+1),f[r].se});} return (f[n].fi+f[n].se*mid<=n-k)&&(f[n].se<=k);
}
signed main(){n=read(),k=read(),S=read();int maxn=0;for(int i=1,lst=0;i<=n;i++){a[i]=read()+a[i-1];if(a[i]-a[lst]>=S) maxn++,lst=i;}int l=0,r=n+5,mid,K;while(l<=r){mid=(l+r)>>1;if(check(mid)) K=mid,l=mid+1;else r=mid-1;}assert(check(K));int s=f[n].fi+f[n].se*K,x=f[n].se;while(x<=maxn&&x<=k&&s<=n-k) x++,s+=K;printf("%lld\n",x-1);return 0;
}
[IOI 2016] aliens
wqs 二分博客怎么能没有 aliens 呢。
不难发现如果要覆盖 \((x,y)\) 这个点必定要覆盖主对角线上区间 \([\min(x,y),\max(x,y)]\) 上的点,所以问题相当于变成了给你一个长度为 \(m\) 的数轴,数轴上有 \(n\) 个线段,要求选出至多 \(k\) 个区间(实际上一定会用恰好 \(k\) 个)使得每个线段都至少被一个区间包含。
显然有包含关系的线段可以去掉被包含的那条,所以把线段左端点排序右端点也升序,下面用 \(l_i,r_i\) 指代排序之后第 \(i\) 个线段的左右端点。
于是可以列出 DP,设 \(f_{i,j}\) 表示覆盖前 \(i\) 条线段,用了 \(j\) 个区间的最小代价,则 \(f_{i,j}=\min_{0\le k<i} f_{k,j-1}+w(k,i)\)。
其中 \(w(a,b)=(r_b-l_{a+1}+1)^2-[a>0 \cap r_a\ge l_{a+1}](r_a-l_{a+1}+1)^2\),其中后半部分是减去重叠部分的贡献。
显然前半部分满足四边形不等式,而后半部分在四边形不等式中会被消掉,所以 \(w(a,b)\) 满足四边形不等式,所以是凸的,可以 wqs 二分。
check 内部和 II.忘情 一样是个简单的斜率优化,复杂度 \(O(n\log n)\)。
点击查看代码
int n,m,k,cnt,w[N],dq[N],l,r;
PII f[N];
int qp(int x){return x*x;}
struct P{int l,r;
}t[N],a[N];
int x(int j){return 2*a[j+1].l;}
int y(int j){return f[j].fi+qp(a[j+1].l)-2*a[j+1].l-w[j];}bool check(int mid){f[0]={0,0};dq[l=r=1]=0;for(int i=1;i<=n;i++){while(l<r && a[i].r*(x(dq[l+1])-x(dq[l]))>(y(dq[l+1])-y(dq[l]))) l++;int j=dq[l]; f[i]=mk(f[j].fi+qp(a[i].r-a[j+1].l+1)-w[j]-mid,f[j].se+1);while(l<r && (y(i)-y(dq[r]))*(x(dq[r])-x(dq[r-1])) < (x(i)-x(dq[r]))*(y(dq[r])-y(dq[r-1]))) r--;dq[++r]=i;}return f[n].se<=k;
}
signed main(){n=read(),m=read(),k=read();for(int i=1;i<=n;i++){int x=read(),y=read();t[i]={min(x,y),max(x,y)};}sort(t+1,t+n+1,[&](P x,P y){return (x.l==y.l)?(x.r>y.r):(x.l<y.l);});for(int i=1,maxn=-1;i<=n;i++) if(maxn<t[i].r) maxn=t[i].r,a[++cnt]=t[i];swap(n,cnt);for(int i=0;i<n;i++) w[i]=(i>0&&a[i].r>=a[i+1].l)*qp(a[i].r-a[i+1].l+1);int l=-inf,r=0,mid,res;while(l<=r){mid=(l+r)>>1;if(check(mid)) l=mid+1,res=mid;else r=mid-1;}assert(check(res));printf("%lld\n",f[n].fi+res*k);return 0;
}






)
)









)












超详细安装教程)






)
)







)



