**交并比(Intersection over Union, IoU)** 是计算机视觉领域中常用的一个评价指标,尤其在目标检测与图像分割任务中,用于衡量预测结果与真实标注之间的重合程度。
目标检测 | 基于Weiler–Atherton算法的IoU求解
IoU
交并比(Intersection over Union, IoU) 是计算机视觉领域中常用的一个评价指标,尤其在目标检测与图像分割任务中,用于衡量预测结果与真实标注之间的重合程度。
其定义如下:

- 如图所示给定任意两个多边形框\(B_1, B_2\)(预测框与真实框),其 IoU 的计算公式为:
\[\text{IoU}(B_1, B_2) = \frac{|B_1 \cap B_2|}{|B_1 \cup B_2|}
\]
其中\(|B_1 \cup B_2|\)为二者并集的面积,\(|B_1 \cap B_2|\)为二者交集的面积。
IoU的取值范围为\([0,1]\),当\(IoU=1\)时表示预测框与真实框完全一致;当\(IoU=0\)时表示预测框与真实框没有任何重叠;
通过评价\(IoU\)可以评估目标检测模型的性能
基于Weiler–Atherton算法的IoU求解
Bounding Box
在目标检测任务中,通常使用 包围盒(bounding box) 表示目标的矩形区域。根据任务需求的不同,包围盒可以分为以下几类:
-
轴对齐包围盒(Axis-Aligned Bounding Box,AABB)
轴对齐包围盒一般应用于2D的目标检测任务,四条边分别与x轴和y轴对齐,可以表达为:
\[B_\text{AABB} = (x_c, y_c, w, h),
\quad w > 0, \, h > 0
\]
- 其中\((x_c,y_c)\)为中心坐标,\(w,h\)分别为包围盒的宽和高,也被称为外延(extent)
-
BEV包围盒(Bird’s Eye View Bounding Box,BEV Boudning Box)
BEV包围盒一般用于自动驾驶任务,在俯视图(BEV)中,每个物体除了位置和尺寸外,还包含一个航向角(yaw)表示方向,可以表达为:
\[B_\text{BEV} = (x_c, y_c, l, w, \theta),
\quad l > 0, \, w > 0, \, \theta \in [-\pi, \pi)
\]
- 其中\((x_c,y_c)\)为中心坐标,\(l,w\)分别为包围盒的长和宽,\(\theta\)为全局坐标系的旋转角度
-
3D包围盒(3D Boudning Box)
3D包围盒在BEV包围盒的基础上增加了高度,也是自动驾驶任务中常用的表示格式
\[B_\text{3D} = (x_c, y_c, z_c, l,w,h, \theta),
\quad w, l, h > 0, \, \theta \in [-\pi, \pi)
\]
- 其中\((x_c,y_c,z_c)\)为中心坐标,\(l,w,h\)分别为包围盒的长,宽和高,\(\theta\)为全局坐标系的旋转角度
在本文中,我们以 BEV 包围盒 为例,使用 Weiler–Atherton 算法求解 IoU。对于3D包围盒的 IoU 计算,可通过将 BEV 包围盒在俯视平面上的结果拓展到高度方向来实现。
Corner坐标转换
在计算之前,我们首先需要将多边形从包围盒表示转换为Corner坐标表示(四个顶点的坐标),这个过程可以分为三步,首先给定一个包围盒:
\[B_\text{BEV} = (x_c, y_c, l, w, \theta),
\quad l > 0, \, w > 0, \, \theta \in [-\pi, \pi)
\]
计算局部坐标系下的四个角点
\[P^\text{local} =
\begin{bmatrix}
+\frac{l}{2} & +\frac{w}{2} \\
+\frac{l}{2} & -\frac{w}{2} \\
-\frac{l}{2} & -\frac{w}{2} \\
-\frac{l}{2} & +\frac{w}{2}
\end{bmatrix} \in \mathbb{R}^{4\times 2}
\]
绕中心旋转矩阵
\[P^\text{rotated} = P^\text{local} \cdot R(\theta)^\top
\]
其中:
\[R(\theta) =
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\]
平移到全局坐标系
\[P^\text{global}=P^\text{rotated}+
\begin{bmatrix} x_c & y_c \\ x_c & y_c \\ x_c & y_c \\ x_c & y_c \end{bmatrix}
\]
将上述的三个过程合并为齐次坐标系矩阵:
\[\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1 \\
x_4 & y_4 & 1
\end{bmatrix} =
\begin{bmatrix}
+ \frac{l}{2} & + \frac{w}{2} & 1 \\
+ \frac{l}{2} & - \frac{w}{2} & 1 \\
- \frac{l}{2} & - \frac{w}{2} & 1 \\
- \frac{l}{2} & + \frac{w}{2} & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
\cos\theta & \sin\theta & x_c \\
-\sin\theta & \cos\theta & y_c \\
0 & 0 & 1
\end{bmatrix}
\]
Weiler–Atherton算法
Weiler–Atherton算法是一种计算任意两个非凹图形交集的算法,可以被分为四个步骤:
- 求解所有相交点
- 求解所有被包围的顶点
- 将相交点和被包围的顶点放入一个数组中,按照逆时针进行排序
- 按照顺序连接为新的多边形求解其面积
给定任意两个包围盒的Cornor坐标表示\(B_1,B_2\in\mathbb{R}^{4 \times 2}\)

计算所有相交点
给定任意两条线段\(L_1=(x_1,y_1),L_2=(x_2,y_2)\)与\(M_1=(x_3,y_3),M_2=(x_4,y_4)\),我们可以如下求出其交点:
定义\(r=L_2-L_1,s=M_2-M_1\),有:
\[t=\frac{(M_1-L_1)\times s}{r\times s},u=\frac{(M_1-L_1)\times r}{r\times s}
\]
其中\(\times\)为二维向量叉乘,定义如下:
\[(x_1,y_1)\times(x_2,y_2)=x_1y_2 - y_1x_2
\]
那么线段\(P,Q\)的交点为:
\[P_{insect}=
\begin{cases}
L_1 + t r, &
\text{if } r\times s \neq 0 \text{ and } t \in [0,1], u \in [0,1] \\[1ex]
\text{无交点}, & \text{otherwise}
\end{cases}
\]
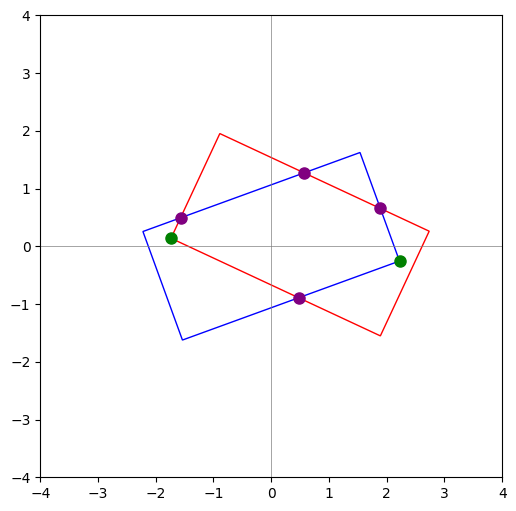
通过线段相交算法我们可以求出任意两个线段之间的交点(如图所示的紫色点)

计算所有被对方包围起来的顶点
给定任意一个包围盒\(B\in\mathbb{R}^{4 \times 2}\)与点\(P\),我们可以通过如下过程求解点\(P\)是否在包围盒\(B\)中:
定义\(P_a=B[0, :],P_b=B[1, :],P_d=B[3, :]\)
求得:
\[t=\frac{AP\cdot AB}{||AB||^2},u=\frac{AP\cdot AD}{||AD||^2}
\]
其中\(AB=P_b-P_a,\ AD=P_d-P_a,\ AP = P-P_a\)
如图所示,当\(t\in[0,1]\and u\in[0,1]\)时,点\(P\)位于包围盒中\(B\)

通过上述流程我们可以求解所有在对方包围盒的顶点(如图所示的绿色点)
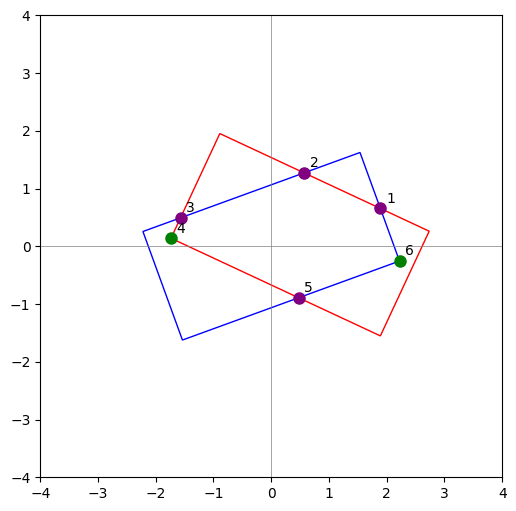
顶点极角排序
为了方便连接每个顶点,接下来我们将所有顶点按照极坐标系下的角度进行排序,给定任意两点\(P_1(x_1,y_1)\)与\(P_2(x_2,y_2)\),有比较函数如下:
\[\text{cmp}(P_1,P_2) =
\begin{cases}
\text{true}, & \Theta_{P_1} < \Theta_{P_2} \\[0.5em]
\text{false}, & \Theta_{P_1} \geq \Theta_{P_2} \\[0.5em]
\end{cases}
\]
其中
\[\Theta_P =
\begin{cases}
\arctan2(y, x), & \arctan2(y, x) \ge 0 \\
\arctan2(y, x) + 2\pi, & \arctan2(y, x) < 0
\end{cases}
\]
但是\(\arctan2\)这个操作非常消耗资源,所以我们不会直接计算极角$\theta $,我们会进行如下优化:
给定极坐标系的坐标$(r,\theta) \(,我们可以构建一个关于\)\theta\(的函数\)g(\theta)=|\cos\theta|\cos\theta$,这个函数会在第一,二象限递减,第三,四象限递增,接下来有:
\[\begin{align}g(\theta) & = \frac{r^2}{r^2} \, g(\theta) \\& =\frac{r^2 \, |\cos\theta| \cos\theta}{r^2}\\& =\frac{|r \cos\theta| \cdot (r \cos\theta)}{r^2} \\
\end{align}
\]
其中我们将极坐标系公式代入原式:
\[x = r \cos\theta, \quad y = r \sin\theta, \quad r = \sqrt{x^2 + y^2}
\]
得到:
\[\begin{align}
g(\theta) &=\frac{|r \cos\theta| \cdot (r \cos\theta)}{r^2} \\&=\frac{|x|\cdot x}{x^2+y^2}
\end{align}
\]
在实际计算中为了防止除0我们会在分母加上一个非常小的数\(\varepsilon\):
\[g(\theta) =\frac{|x|\cdot x}{x^2+y^2+\varepsilon}
\]
我们可以给出优化版本的比较函数\(\text{cmp}(\cdot,\cdot)\):
\[\text{cmp}(P_1,P_2) =
\begin{cases}
\text{false}, & (x_1,y_1) = (x_2,y_2) \\[0.5em]
\text{true}, & y_1 > 0,\, y_2 < 0 \\[0.5em]
\text{false}, & y_1 < 0,\, y_2 > 0 \\[0.5em]
\text{true}, & y_1 > 0,\, y_2 > 0,\, g(\theta_1) > g(\theta_2) \\[0.5em]
\text{true}, & y_1 < 0,\, y_2 < 0,\, g(\theta_1) < g(\theta_2) \\[0.5em]
\end{cases}\text{其中 }
g(\theta) = \frac{|x|\cdot x}{x^2+y^2+\varepsilon}
\]
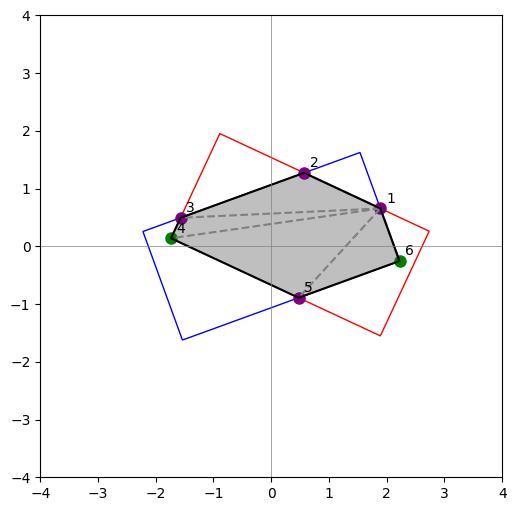
形成新的多边形并计算面积
给定任意二维向量\(L=(x_1,y_1),M=(x_2,y_2)\),我们可以求解二者共同起点所构成的三角形面积\(S_{LM}\):
\[S_{LM}=\frac{1}{2}|L\times M|=\frac{1}{2}|x_1y_2-y_1x_2|
\]
给定已经按照极角进行排序的点集\(\{P_1,\dots,P_n|n\leq8\}\),我们可以将这些点按照顺序连接为一个闭合的多边形\(I\),这个多边形由\(n-2\)个三角形所组成,每个三角形\(S_n\)的面积为\(S_n=\frac{1}{2}|(P_{n+1}-P_1)\times (P_{n+2}-P_1)|\),那么我们可以算出这个多边形的面积:
\[S_{I}=\sum^{n-2}_{i=1}\frac{1}{2}|(P_{i+1}-P_1)\times (P_{i+2}-P_1)|
\]

计算IoU
上文我们已经得到BEV包围盒\(B_1\)与\(B_2\)的交集面积为\(S_I\),那么我们可以如下算得\(IoU\):
\[IoU =\frac{Intersection}{Union}= \frac{S_I}{S_{B_1}+S_{B_2}-S_I}
\]
如果\(B_1,B_2\)为3D包围盒,可以如下增加一个高度项:
\[IoU =\frac{Intersection}{Union}= \frac{H_I}{H_U}\frac{S_I}{S_{B_1}+S_{B_2}-S_I}
\]
其中
\[\begin{align}
H_I=&\max(0,\min(z_{B_1}+\frac{h_{B_1}}{2}, z_{B_1}+\frac{h_{B_2}}{2})-\max(z_{B_1}-\frac{h_{B_1}}{2},z_{B_2}-\frac{h_{B_2}}{2}))\\H_U=&h_{B_1}+h_{B_2}-H_I
\end{align}
\]
参考文献
https://en.wikipedia.org/wiki/Weiler–Atherton_clipping_algorithm
https://github.com/lilanxiao/Rotated_IoU












-MRT专业的工具替代)












)



























:基础篇(线程池的核心原理是什么、线程池大小设置为多少更合适、线程池哪几种类型?ThreadLocal为什么会导致内存泄漏?) - 实践)




