【机器学习】支持向量机(SVM)
目录
一、支持向量机基本概念
1.1 定义
1.2 支持向量:距离超平面最近的样本点,决定了超平面的位置。
二、线性支持向量机
2.1 硬间隔支持向量机
2.2 软间隔支持向量机
三、非线性支持向量机
3.1 核函数
3.2 常用核函数
3.2.1 线性核:等价于线性SVM,适合线性可分数据。
3.2.2 多项式核:适合数据具有多项式关系,参数c>=0控制常数项,d控制多项式阶数
3.2.3 高斯核(RBF核):适合复杂非线性数据,参数 控制映射的局部性。
3.2.4 Sigmoid核:类似神经网络激活函数,参数,c控制形状
四、实战:SVM垃圾邮件分类器实现
4.1 项目分析
4.2 代码实现
4.3 结果显示(可视化)
一、支持向量机基本概念
1.1 定义
SVM是一种基于统计学习理论的监督学习模型,旨在找到一个最优超平面,将不同类别的数据点分隔开,同时最大化分类间隔(Margin)
具体来说:
- 在线性可分时,在原空间寻找两类样本的最优分类超平面。
- 在线性不可分时,加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分,这样就可以在该特征空间中寻找最优分类超平面。
1.2 支持向量:距离超平面最近的样本点,决定了超平面的位置。
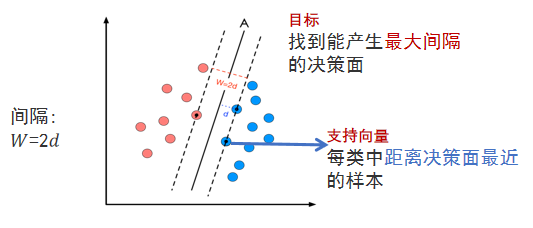
二、线性支持向量机
线性支持向量机假设数据是线性可分的,目标是找到一个超平面,将不同类别的数据点分隔开,并最大化分类间隔。
2.1 硬间隔支持向量机
适用场景:数据完全线性可分,无噪声干扰。
目标:找到一个超平面,使得所有数据点被正确分类,且到最近数据点(支持向量)的间隔最大。

(1)超平面:
(2)间隔:数据点
到超平面的距离为
。
支持向量是距离超平面最近的点,满足:
(3)最大化间隔等价于使
最大,即最小化
优化目标:最小化法向量范数的平方
约束条件:确保所有数据点被正确分类且位于间隔边界之外
其中
是数据点,
是类别标签,w是法向量,b是偏置
拉格朗日对偶问题:
- 引入拉格朗日乘子𝛼𝑖≥0,构造拉格朗日函数:
- 对w和b求偏导并令其为0:
- 代回拉格朗日函数,得到对偶问题:
- 约束条件:
求解方法:使用序列最小优化(SMO)算法等方法求解
,然后计算w和b。
预测:对于新数据点x,分类决策函数为:
2.2 软间隔支持向量机
适用场景:数据近似线性可分,存在噪声或少量误分类点。
核心思想:引入松弛变量,允许部分数据点位于间隔内或被误分类,通过惩罚参数C平衡间隔最大化与误分类最小化。

优化目标:最小化法向量范数的同时,控制误分类的惩罚
约束条件:允许数据点偏离正确分类的间隔
其中,C>0是惩罚参数,
是松弛变量,表示数据点偏离正确分类的程度
几何意义:
𝜉𝑖=0:数据点正确分类且在间隔外。
0<ξi≤1:数据点在间隔内但分类正确。
ξi>1:数据点被误分类。
C 控制间隔大小与误分类的权衡:C 越大,惩罚误分类越多,模型更严格;C 越小,允许更多误分类,间隔更大。
拉格朗日对偶问题:
- 构造拉格朗日函数:
- 对w,b,
求偏导并令其为0:
- 代回得到对偶问题:
- 约束条件:
求解方法:使用序列最小优化(SMO)算法等方法求解
,然后计算w和b。
预测:对于新数据点x,分类决策函数为:
三、非线性支持向量机
当数据线性不可分时(例如,数据点在二维空间呈环形或交叉分布),通过核函数将数据映射到高维空间,使其在高维空间中线性可分。

3.1 核函数
核心思想:
-
显式映射到高维空间计算复杂,核函数通过计算低维空间的内积 𝐾(𝑥𝑖,𝑥𝑗)=𝜙(𝑥𝑖)𝑇𝜙(𝑥𝑗)替代高维计算。
-
核函数满足Mercer条件(正定性),确保对偶问题的凸性。
数学表述:
对偶问题与软间隔SVM一致,但用核函数替换内积
约束条件:
决策函数:
3.2 常用核函数
3.2.1 线性核:等价于线性SVM,适合线性可分数据。
3.2.2 多项式核:适合数据具有多项式关系,参数c>=0控制常数项,d控制多项式阶数
3.2.3 高斯核(RBF核):适合复杂非线性数据,参数 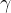 控制映射的局部性。
控制映射的局部性。
越大,模型越倾向于拟合局部数据(可能过拟合);
越小,模型更平滑。
3.2.4 Sigmoid核:类似神经网络激活函数,参数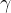 ,c控制形状
,c控制形状

四、实战:SVM垃圾邮件分类器实现
4.1 项目分析
任务:构建一个垃圾邮件分类器,用于区分垃圾邮件(y=1)和非垃圾邮件(y=0)。
方法:使用支持向量机(SVM)分类器,尝试不同的核函数(线性核、多项式核、RBF核)。
数据:
- vocab.txt:词汇表,包含1899个单词及其索引。
- emailSample1.txt:示例邮件,用于测试特征提取。
- spamTrain.mat 和 spamTest.mat:预处理后的训练和测试数据集,包含1899维二值特征向量和标签。
可视化:通过PCA降维到2D,绘制SVM的决策边界,展示不同核函数的分类效果。
4.2 代码实现
import numpy as np
import scipy.io
import re
import os
from sklearn.svm import SVC
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import matplotlib# 设置 Matplotlib 支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False# 步骤 1:加载词汇表
def load_vocabulary(vocab_file):"""从 vocab.txt 加载词汇表(单词到索引的映射)。"""if not os.path.exists(vocab_file):raise FileNotFoundError(f"文件 {vocab_file} 不存在,请检查路径或文件是否正确。")vocab = {}with open(vocab_file, 'r', encoding='utf-8') as f:for line in f:index, word = line.strip().split()vocab[word] = int(index)return vocab# 步骤 2:将邮件转换为特征向量
def process_email(email_content, vocab):"""将邮件文本转换为 1899 维二值特征向量。"""feature_vector = np.zeros(len(vocab))email_content = email_content.lower()email_content = re.sub(r'[^\w\s]', '', email_content)words = email_content.split()for word in words:if word in vocab:feature_vector[vocab[word] - 1] = 1return feature_vector# 步骤 3:加载训练和测试数据
def load_mat_data(train_file, test_file):"""加载 spamTrain.mat 和 spamTest.mat。"""if not os.path.exists(train_file):raise FileNotFoundError(f"文件 {train_file} 不存在,请检查路径。")if not os.path.exists(test_file):raise FileNotFoundError(f"文件 {test_file} 不存在,请检查路径。")train_data = scipy.io.loadmat(train_file)test_data = scipy.io.loadmat(test_file)X_train = train_data.get('X', train_data.get('Xtest'))y_train = train_data.get('y', train_data.get('ytest')).ravel()X_test = test_data.get('X', test_data.get('Xtest'))y_test = test_data.get('y', test_data.get('ytest')).ravel()return X_train, y_train, X_test, y_test# 步骤 4:训练和评估 SVM
def train_svm(X_train, y_train, X_test, y_test, kernel='linear', **kwargs):"""训练 SVM 分类器并评估准确率。"""clf = SVC(kernel=kernel, **kwargs)clf.fit(X_train, y_train)train_accuracy = clf.score(X_train, y_train)test_accuracy = clf.score(X_test, y_test)return clf, train_accuracy, test_accuracy# 步骤 5:可视化 2D 决策边界(美化版)
def plot_decision_boundary(X, y, clf, kernel_name):"""使用 PCA 降维到 2D 并绘制美化的决策边界。"""# PCA 降维到 2Dpca = PCA(n_components=2)X_2d = pca.fit_transform(X)# 训练 2D 分类器params = clf.get_params()clf_2d = SVC(**params)clf_2d.fit(X_2d, y)# 创建网格h = 0.05 # 增大步长,减少计算量并平滑边界x_min, x_max = X_2d[:, 0].min() - 1, X_2d[:, 0].max() + 1y_min, y_max = X_2d[:, 1].min() - 1, X_2d[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# 预测网格点类别Z = clf_2d.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# 创建画布并设置大小plt.figure(figsize=(10, 8), dpi=100)# 绘制决策边界(使用更柔和的配色)plt.contourf(xx, yy, Z, levels=[-1, 0, 1], colors=['#A3BFFA', '#FECACA'], alpha=0.5)plt.contour(xx, yy, Z, levels=[0], colors='gray', linestyles='--', linewidths=2)# 绘制数据点(分别绘制两类,添加标签用于图注)spam = y == 1non_spam = y == 0plt.scatter(X_2d[non_spam, 0], X_2d[non_spam, 1], c='#3B82F6', s=30, alpha=0.6, edgecolors='white',label='非垃圾邮件')plt.scatter(X_2d[spam, 0], X_2d[spam, 1], c='#EF4444', s=30, alpha=0.6, edgecolors='white', label='垃圾邮件')# 设置标题和标签(增大字体,调整样式)plt.title(f'SVM 决策边界 ({kernel_name})', fontsize=16, pad=15)plt.xlabel('主成分 1', fontsize=14)plt.ylabel('主成分 2', fontsize=14)# 添加图注plt.legend(loc='upper right', fontsize=12, frameon=True, shadow=True)# 添加网格线plt.grid(True, linestyle='--', alpha=0.7)# 调整刻度字体plt.tick_params(axis='both', which='major', labelsize=12)# 设置边框样式ax = plt.gca()ax.spines['top'].set_linewidth(1.5)ax.spines['right'].set_linewidth(1.5)ax.spines['left'].set_linewidth(1.5)ax.spines['bottom'].set_linewidth(1.5)# 保存图像plt.savefig(f'decision_boundary_{kernel_name.lower()}.png', bbox_inches='tight')plt.close()# 主函数
def main():# 文件路径vocab_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/vocab.txt'train_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/spamTrain.mat'test_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/spamTest.mat'email_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/emailSample1.txt'# 检查文件是否存在for file in [vocab_file, email_file, train_file, test_file]:if not os.path.exists(file):print(f"错误:文件 {file} 不存在,请检查路径。")return# 加载词汇表vocab = load_vocabulary(vocab_file)print(f"词汇表大小: {len(vocab)}")# 处理示例邮件with open(email_file, 'r', encoding='utf-8') as f:email_content = f.read()sample_features = process_email(email_content, vocab)print(f"示例邮件特征向量维度: {sample_features.shape}")# 加载训练和测试数据X_train, y_train, X_test, y_test = load_mat_data(train_file, test_file)print(f"训练数据维度: {X_train.shape}, 测试数据维度: {X_test.shape}")# 定义核函数和参数kernels = [('线性核', {'kernel': 'linear', 'C': 1.0}),('多项式核', {'kernel': 'poly', 'degree': 3, 'C': 1.0}),('RBF核', {'kernel': 'rbf', 'gamma': 'scale', 'C': 1.0})]# 训练并评估 SVMfor kernel_name, params in kernels:print(f"\n正在训练 {kernel_name} 的 SVM 模型...")clf, train_acc, test_acc = train_svm(X_train, y_train, X_test, y_test, **params)print(f"{kernel_name} - 训练集准确率: {train_acc:.4f}, 测试集准确率: {test_acc:.4f}")plot_decision_boundary(X_train, y_train, clf, kernel_name)print(f"决策边界图已保存为 'decision_boundary_{kernel_name.lower()}.png'")if __name__ == "__main__":main()4.3 结果显示(可视化)

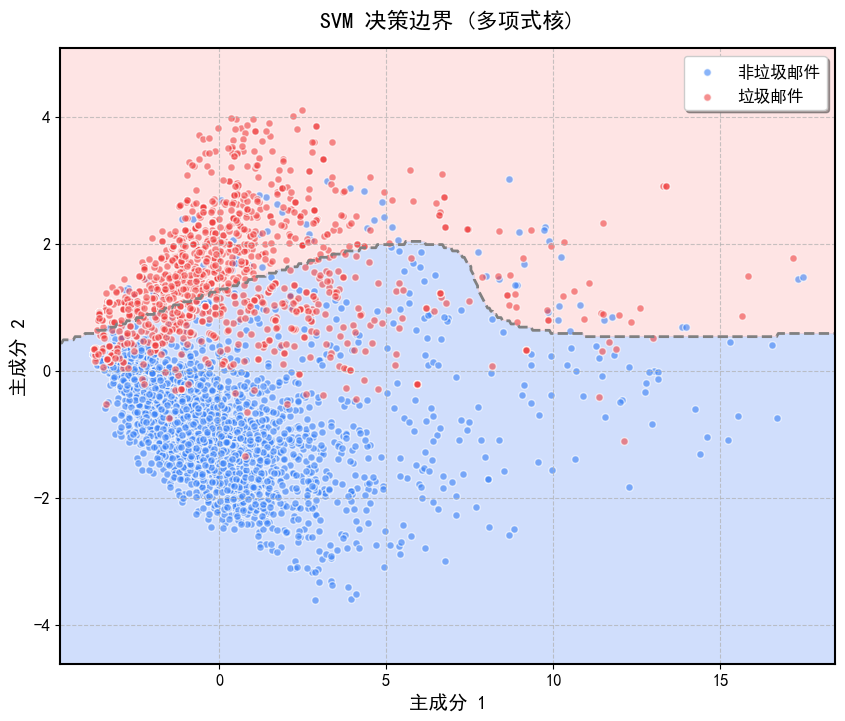

相关文章:
)
【机器学习】支持向量机(SVM)
目录 一、支持向量机基本概念 1.1 定义 1.2 支持向量:距离超平面最近的样本点,决定了超平面的位置。 二、线性支持向量机 2.1 硬间隔支持向量机 2.2 软间隔支持向量机 三、非线性支持向量机 3.1 核函数 3.2 常用核函数 3.2.1 线性核:…...
)
[Java实战]Spring Boot整合MinIO:分布式文件存储与管理实战(三十)
[Java实战]Spring Boot整合MinIO:分布式文件存储与管理实战(三十) 一、MinIO简介与核心原理 MinIO 是一款高性能、开源的分布式对象存储系统,兼容 Amazon S3 API,适用于存储图片、视频、日志等非结构化数据。其核心特…...

SpringBoot微服务编写Dockerfile流程及问题汇总
背景 跟 Docker 磕了两天,将一个包含 N 个微服务的应用部署包改造,使其能够生成 Docker 镜像,并在 Docker 容器中运行。几年前玩过 Docker,隐约记得几个命令「Dockerfile 命令:黑卡饮料、山楂果费、哦SUV,…...

PostgreSQL使用
一、PostgreSQL语法 PostgreSQL表、模式、库三者之间的关系 库 -> 模式 -> 表、视图、函数等等对象。 在postgresql的交互式终端psql中,“\”开头的命令称为元命令(类似mysql的show语句),用于快速管理数据库。 常见元命令&…...

现代化SQLite的构建之旅——解析开源项目Limbo
现代化SQLite的构建之旅——解析开源项目Limbo 在当今飞速发展的技术世界中,轻量级且功能强大的数据库已成为开发者的得力助手。当我们谈论轻量级数据库时,SQLite无疑是一个举足轻重的名字。然而,随着技术的进步,我们对数据库的需…...

MySQL 主从复制搭建全流程:基于 Docker 与 Harbor 仓库
一、引言 在数据库管理中,MySQL 主从复制是一种非常重要的技术,它可以实现数据的备份、读写分离,减轻主数据库的压力。本文将详细介绍如何使用 Docker 和 Harbor 仓库来搭建 MySQL 主从复制环境,适合刚接触数据库和 Docker 的新手…...

网页表格转换为markdown
网页表格到Markdown:一键转换,复制即用! 在日常工作中,我们经常需要从网页上复制表格数据,并将其转换成Markdown格式,以便在文档、邮件或论坛中使用。然而,手动转换不仅耗时,还容易…...

MySQL字符串拼接方法全解析
目录 常用字符串处理函数 方法一:CONCAT基础拼接 方法二:CONCAT_WS带分隔符拼接 方法三:GROUP_CONCAT分组拼接 方法四:算术运算符拼接(仅限数字) 常用字符串处理函数 方法一:CONCAT基础拼接…...

零基础教程:用 Docker + pgloader 将 MySQL 数据库迁移到 PostgreSQL
在日常开发中,可能会遇到从 MySQL 迁移到 PostgreSQL 的需求。你也许是: 正在准备从传统架构转向云原生;想使用 PostgreSQL 更强的事务与 JSON 支持;想统一团队数据库技术栈;纯粹为了尝试学习不同的数据库系统。 别担…...

影刀Fun叉鸟-2048
文章目录 仅为自动化演示,实际2048判定逻辑需要更加严谨 参考代码 # 使用提醒: # 1. xbot包提供软件自动化、数据表格、Excel、日志、AI等功能 # 2. package包提供访问当前应用数据的功能,如获取元素、访问全局变量、获取资源文件等功能 # 3. 当此模块作…...
:页面)
uni-app(2):页面
1 页面简介 uni-app项目中,一个页面就是一个符合Vue SFC规范的 vue 文件。 在 uni-app js 引擎版中,后缀名是.vue文件或.nvue文件。 这些页面均全平台支持,差异在于当 uni-app 发行到App平台时,.vue文件会使用webview进行渲染&…...

【spring】spring学习系列之十一:spring的事件监听
系列文章目录 文章目录 系列文章目录前言一、使用二、整体流程三、EventListenerMethodProcessor和DefaultEventListenerFactory1.EventListenerMethodProcessor2.DefaultEventListenerFactory3.ApplicationListenerDetector4.initApplicationEventMulticaster5.registerListen…...
)
代码随想录打卡|Day45 图论(孤岛的总面积 、沉没孤岛、水流问题、建造最大岛屿)
图论part03 孤岛的总面积 代码随想录链接 题目链接 视频讲解链接 思路:既然某个网格在边界上的岛屿不是孤岛,那么就把非 孤岛的所有岛屿变成海洋,最后再次统计还剩余的岛屿占据的网格总数即可。 dfs: import java.util.Scanner…...

AI人工智能——Matplotlib绘制各种数据可视化图表的基础方法
一、绘制图像基础 import matplotlib.pyplot as plt# 1、创建画布 plt.figure(figsize(20, 8), dpi100) # 2、绘制图像 x [1, 2, 3, 4, 5, 6] y [3, 5, 4, 3, 6, 1] plt.plot(x, y) # 3、显示图像 plt.show() 二、图像保存 import matplotlib.pyplot as plt# 1、创建画布 p…...

亚马逊AWS跑不动了?
5月2日,亚马逊公布了2025年第一季度的财报。财报数据显示,云计算业务增速放缓以及第二季度的指引低于预期。事实上,这并不是亚马逊AWS第一次增速放缓。 亚马逊AWS作为全球第一大云计算服务公司,这些年跟微软云、谷歌云等其他云计…...

PyTorch中cdist和sum函数使用详解
torch.cdist 是 PyTorch 中用于计算**两个张量之间的成对距离(pairwise distance)**的函数,常用于点云处理、图神经网络、相似性度量等场景。 基本语法 torch.cdist(x1, x2, p2.0)参数说明: 参数说明x1一个形状为 [B, M, D] 或 …...

PyTorch的基本操作
前言 为了方便大家学习,我整理了PyTorch全套学习资料,包含配套教程讲义和源码 除此之外还有100G人工智能学习资料 包含数学与Python编程基础、深度学习机器学习入门到实战,计算机视觉自然语言处理大模型资料合集,不仅有配套教程…...

分类算法 Kmeans、KNN、Meanshift 实战
任务 1、采用 Kmeans 算法实现 2D 数据自动聚类,预测 V180,V260 数据类别; 2、计算预测准确率,完成结果矫正 3、采用 KNN、Meanshift 算法,重复步骤 1-2 代码工具:jupyter notebook 视频资料 无监督学习ÿ…...

aws平台s3存储桶夸域问题处理
当我们收到开发反馈s3存在跨域问题 解决步骤: 配置 S3 存储桶的 CORS 设置: 登录到 AWS 管理控制台。转到 S3 服务。选择你存储文件的 存储桶。点击 权限 标签页。在 跨域资源共享(CORS)配置 部分,点击 编辑。 登陆…...

在Windows上安装Pygame 2.1.3:解决常见问题
在Windows系统上安装Pygame 2.1.3时,可能会遇到各种问题,例如网络问题或依赖安装失败。本文将详细介绍如何在Windows上成功安装Pygame 2.1.3,并解决常见的安装问题。 1. 前提条件 在开始安装之前,确保你的系统中已经安装了Pytho…...
,tomcat)
linux中安装jdk(Java环境),tomcat
安装时候选择 tomcat 软件版本要与程序开发使用的版本一致。jdk 版本要进行与 tomcat 保持一致。 1. 系统环境说明 [root@bogon ~]# getenforce Disabled [root@bogon ~]# systemctl status firewalld.service ● firewalld.service - firewalld - dynamic firewall daemon …...

DeepSeek源码解构:从MoE架构到MLA的工程化实现
文章目录 **一、代码结构全景:从模型定义到分布式训练****二、MoE架构:动态路由与稀疏激活的工程化实践****1. 专家路由机制(带负载均衡)****数学原理:负载均衡损失推导** **三、MLA注意力机制:低秩压缩与解…...
使用 PageOffice实现PDF文件加盖印章和签字功能)
国产linux系统(银河麒麟,统信uos)使用 PageOffice实现PDF文件加盖印章和签字功能
PageOffice 国产版 :支持信创系统,支持银河麒麟V10和统信UOS,支持X86(intel、兆芯、海光等)、ARM(飞腾、鲲鹏、麒麟等)、龙芯(Mips、LoogArch)芯片架构。 PageOffice支持…...
)
第四十三节:人脸检测与识别-人脸识别基础 (Eigenfaces, Fisherfaces, LBPH)
引言 人脸识别技术是计算机视觉领域最具应用价值的方向之一,广泛应用于安防监控、身份认证、人机交互等领域。本文将通过OpenCV框架,深入解析人脸检测与识别的核心算法(Eigenfaces/Fisherfaces/LBPH),并提供完整的代码实现。 第一部分:人脸检测基础 1.1 人脸检测原理 …...
)
面向恶劣条件的道路交通目标检测----大创自用(当然你也可以在里面学到很多东西)
全部内容梳理 目标检测的两个任务: 预测标签 边界框 语义分割 实力分割 一个是类别 一个是实例级别 分类任务把每个图像当作一张图片看待 所有解决方法是先生成候选区域 再进行分类 置信度: 包括对类别和边界框预测的自信程度 输出分类和IOU分数的…...

物联网相关词汇
物联网(英文:Internet of Things,缩写:IoT) specs 英[speks] 美[speks] 规格说明 topology 英[təpɒlədʒɪ] 拓扑结构 vertical 美 [ˈvɜrtɪk(ə)l] 英 [ˈvɜː(r)tɪk(ə)l] n.垂直线;垂直位…...
)
【net6】一文跑通前后端以及数据库,简单的天气系统管理(保姆入门)
一、前言 使用Vue3为前端,.net6为后端,连接postgreSQL数据库,连通前后端与数据库,实现最基础的天气管理系统的增删改查。 二、内容 目录 一、前言 二、内容 2.1 后端部分 2.1.1 在VS里面使用此模板创建项目 2.1.2 安装下列…...

宝塔安装的 MySQL 无法连接的情况及解决方案
宝塔安装的 MySQL 无法连接的情况及解决方案 宝塔面板是一款流行的服务器管理工具,其中集成的 MySQL 数据库有时会出现连接问题。本文详细介绍两种最常见的 MySQL 连接错误:“1130 - Host is not allowed to connect” 和 “1045 - Access denied”&…...

【iOS】分类、扩展、关联对象
分类、扩展、关联对象 前言分类扩展扩展和分类的区别关联对象key的几种用法流程 总结 前言 最近的学习中笔者发现自己对于分类、扩展相关知识并不是很熟悉,刚好看源码类的加载过程中发现有类扩展与关联对象详解。本篇我们来探索一下这部分相关知识,首先…...
—— OSI vs TCP/IP网络模型)
计算机网络学习(一)—— OSI vs TCP/IP网络模型
一、OSI模型(开放系统互联参考模型) OSI(Open Systems Interconnection)模型由ISO(国际标准化组织)在1984年提出,用于标准化网络通信,它将网络通信分为七个层次: 层级名…...

【MySQL成神之路】MySQL查询用法总结
MySQL查询语句全面指南 一、基础查询语句 MySQL中select的基本语法形式 select 属性列表 from 表名和视图列表 [where 条件表达式] [group by 属性名[having 条件表达式]] [order by 属性名[asc|desc]] [limit <offset>,row count] 说明: where子句&…...

攻防世界——Web题 fakebook
首先测试网站的功能,当我注册一个账号时,发现这里的链接: 点进去看到URL: 感觉no这个地方可以尝试一下sql注入 推测应该是数字型注入 发现果然可以进行sql注入, 最终测得列数应该是4列,但当我尝试sql注入…...

【Java微服务组件】异步通信P2—Kafka与消息
欢迎来到啾啾的博客🐱。 记录学习点滴。分享工作思考和实用技巧,偶尔也分享一些杂谈💬。 欢迎评论交流,感谢您的阅读😄。 目录 引言Kafka与消息生产者发送消息到Kafka批处理发送设计消息的幂等信息确保消息送达acks配置…...

AI数字人一体机和智慧屏方案:开启智能交互新纪元
在当今这个信息化飞速发展的时代,AI技术正以前所未有的速度改变着我们的生活方式和工作模式。特别是在人机交互领域,AI数字人的出现不仅极大地丰富了用户体验,也为各行各业提供了前所未有的创新解决方案。本文将重点介绍由广州深声科技有限公…...

10-码蹄集600题基础python篇
题目如上: 这题就是ASCII的转换,直接使用ord就可以 下面是代码: def main():#code here# a1,a2input().split(",")# print(f"The ASCII code of {a1} is {ord(a1)}")# print(f"The ASCII code of {a2} is {ord(a2…...

给几张图片和一段文字,怎么制作成带有语音的视频---php
想用PHP将图片和文字转换成带有语音的视频,想做自动化的视频生成,比如用于广告、演示或者其他需要多媒体处理的场景。 接下来考虑PHP本身的能力。PHP主要是用于服务器端的脚本语言,不太擅长处理多媒体内容,比如视频和语音合成。所…...

vue3中RouterView配合KeepAlive实现组件缓存
KeepAlive组件缓存 为什么需要组件缓存代码展示缓存效果为什么不用v-if 为什么需要组件缓存 业务需求:一般是列表页面通过路由跳转到详情页,跳转回来时,需要列表页面展示上次展示的内容 代码展示 App.vue入口 <script setup lang"…...

NIFI的处理器:ExecuteGroovyScript 2.4.0
ExecuteGroovyScript是常用的处理器之一,用于执行GroovyScript脚本。该脚本负责处理传入的流文件(例如传输到SUCCESS或删除)以及由该脚本创建的任何流文件。如果处理不完整或不正确,会话将被回滚。 属性值-失败处理策略 Failure …...

安全可控的AI底座:灯塔大模型应用开发平台全面实现国产信创兼容适配认证
国产信创产品兼容适配认证是为了支持和推动国产信息技术产品和服务的发展而设立的一种质量标准和管理体系。适配认证旨在确保相关产品在安全性、可靠性、兼容性等方面达到一定的标准,以满足政府和关键行业对信息安全和自主可控的需求。 北京中烟创新科技有限公司&a…...
)
.NET外挂系列:5. harmony 中补丁参数的有趣玩法(下)
一:背景 1. 讲故事 开局一张表,故事全靠编,为了能够承上启下,先把参数列表放出来。 参数名说明__instance访问非静态方法的实例(类似 this)。__result获取/修改返回值,要想修改用 ref。__res…...

Spring Boot 登录实现:JWT 与 Session 全面对比与实战讲解
Spring Boot 登录实现:JWT 与 Session 全面对比与实战讲解 2025.5.21-23:11今天在学习黑马点评时突然发现用的是与苍穹外卖jwt不一样的登录方式-Session,于是就想记录一下这两种方式有什么不同 在实际开发中,登录认证是后端最基础也是最重要…...

vscode离线安装组件工具vsix
1.外网下载vsix 网址为:Open VSX Registry 2.输入需要下载的组件 3.下载组件 4.安装 5.选择安装文件 6.安装完成...

Vue大数据量前端性能优化策略
文章目录 前言Vue大数据量前端性能优化策略1. 虚拟列表的使用方式及优势2. 列表和图表的懒加载技术3. Web Worker 在图表数据预处理中的应用4. 图表渲染优化技巧5. 分批渲染技术实现方法(如 requestIdleCallback)6. 其他可行的 Vue 层优化策略 前言 Vue…...

Hass-Panel - 开源智能家居控制面板
文章目录 ▎项目介绍:预览图▎主要特性安装部署Docker方式 正式版Home Assistant Addon方式详细安装方式1. Home Assistant 插件安装(推荐)2. Docker 安装命令功能说明 :3. Docker Compose 安装升级说明Docker Compose 版本升级 功…...

iPaaS集成平台技术选型关注哪些指标?
在数字化转型进程中,企业系统间的数据孤岛问题日益凸显。根据IDC调研,85%的IT决策者将“系统集成效率”列为业务创新的关键瓶颈。iPaaS(集成平台即服务)凭借其敏捷性、低代码特性和智能化能力,已成为企业构建数字生态的…...
:跨端JavaScript性能优化)
JavaScript性能优化实战(14):跨端JavaScript性能优化
在当今多端开发的时代,JavaScript已经突破了浏览器的界限,广泛应用于移动应用、桌面应用、小程序等各类环境。然而,不同平台的运行时环境存在差异,为JavaScript性能优化带来了新的挑战和思考维度。 目录 React Native性能优化最佳实践Electron应用性能优化策略混合应用中J…...

多通道经颅直流电刺激器产品及解决方案特色解析
前记 团队在多通道经颅直流电刺激这个技术方向,一路深耕。在服务了不少客户之后,为了方便后续的产品和方案推广。我们弄出来了产品和方案两种形态。标准产品是为了给用户演示以及一些常规的实验使用。方案则是为了满足不同方向的科研用户的需求。这两者相…...

Quasar 使用 Pinia 进行状态管理
官方文档:使用 Pinia 进行状态管理 |Quasar 框架 视频教程:quasar框架store-状态管理库pinia介绍_哔哩哔哩_bilibili 使用 Quasar CLI 创建一个新的store quasar new store date --format jsPinia存储模板详解解 基本结构解析 import { defineStore,…...
)
计算机网络--第一章(下)
1.计算机网络的分层结构 1.1 分层结构 网络体系结构描述的是,计算机网络有几层,有什么功能,用的什么协议。 水平方向的关系, 协议,说的是对等实体间通信需要遵守的规则。用于约束,这个约束的方向是水平的。…...

Veo 3 可以生成视频,并附带配乐
谷歌最新的视频生成 AI 模型 Veo 3 可以创建与其生成的剪辑相配的音频。 周二,在谷歌 I/O 2025 开发者大会上,谷歌发布了 Veo 3。该公司声称,这款产品可以生成音效、背景噪音,甚至对话,为其制作的视频增添配乐。谷歌表…...
