当前位置： 首页 > news >正文

打卡第二十二天

news 来源：原创 2025/7/19 4:51:46

知识点回顾：

  1. LDA线性判别
  2. PCA主成分分析
  3. t-SNE降维

  4. 还有一些其他的降维方式，也就是最重要的词向量的加工，我们未来再说。

    作业： 自由作业：探索下什么时候用到降维？降维的主要应用？或者让AI给你出题，群里的同学互相学习下。可以考虑对比下在某些特定数据集上t-SNE的可视化和PCA可视化的区别。

什么时候用到降维？降维的主要应用？

数据集类型

降维方法适用于多种类型的数据集，尤其是高维数据集。常见的数据集类型包括：

  • 图像数据：图像数据通常具有高维度，每个像素点可以视为一个特征。降维可以用于图像压缩、特征提取等。
  • 文本数据：文本数据经过向量化后（如TF-IDF、词袋模型）往往具有高维稀疏特征，降维可以用于文本分类、信息检索等。
  • 基因数据：基因表达数据通常具有大量特征（基因），而降维可以帮助识别关键基因或模式。
  • 金融数据：金融市场数据可能包含大量指标和时间序列，降维可以用于风险管理、投资组合优化等。

降维的应用场景

降维技术广泛应用于各个领域，主要目的是简化数据、减少计算复杂度、提高模型性能以及可视化高维数据。

  • 数据可视化：降维可以将高维数据投影到二维或三维空间，便于直观展示和探索数据分布。
  • 特征选择与提取：降维可以去除冗余特征，保留重要特征，提升机器学习模型的效率和精度。
  • 图像处理：在图像识别和计算机视觉中，降维用于特征提取和图像压缩。
  • 自然语言处理：文本数据降维可以用于主题建模、情感分析等任务。
  • 生物信息学：降维用于分析基因表达数据，识别疾病相关的生物标志物。
  • 推荐系统：降维可以简化用户-物品交互矩阵，提高推荐算法的性能。

常用的降维方法

常用的降维方法包括线性降维和非线性降维技术。

  • 主成分分析（PCA）：一种线性降维方法，通过正交变换将数据投影到低维空间。
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

  • t-SNE：一种非线性降维方法，特别适用于高维数据的可视化。
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2)
X_embedded = tsne.fit_transform(X)

  • 线性判别分析（LDA）：一种监督学习的降维方法，适用于分类任务。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
X_reduced = lda.fit_transform(X, y)

  • 自编码器（Autoencoder）：一种基于神经网络的非线性降维方法。
from keras.layers import Input, Dense
from keras.models import Modelinput_layer = Input(shape=(input_dim,))
encoded = Dense(encoding_dim, activation='relu')(input_layer)
decoded = Dense(input_dim, activation='sigmoid')(encoded)
autoencoder = Model(input_layer, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder.fit(X, X, epochs=50, batch_size=256, shuffle=True)

降维方法的选择取决于具体任务和数据集特性，合理使用降维技术可以显著提升数据分析的效率和效果。

t-SNE降维和PCA降维的精度区别

我尝试了心脏病数据集，很显然心脏病数据集并不适应于t-sne降维

首先默认参数随机森林模型

import pandas as pd
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.read_csv(r'C:\Users\许兰\Desktop\打卡文件\python60-days-challenge-master\heart.csv')
import warnings
warnings.filterwarnings("ignore")
plt.rcParams['font.sans-serif'] = ['SimHei']  # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False 
discrete_features = data.select_dtypes(include=['object']).columns.tolist()
from sklearn.model_selection import train_test_split
x = data.drop(['target'],axis=1)
y = data['target']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)import numpy as np # 引入 numpy 用于计算平均值等
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import StratifiedKFold, cross_validate # 引入分层 K 折和交叉验证工具
from sklearn.metrics import make_scorer, accuracy_score, precision_score, recall_score, f1_score, confusion_matrix, classification_report
import time
import warnings
warnings.filterwarnings("ignore")
print("--- 1. 默认参数随机森林 (训练集 -> 测试集) ---")
start_time = time.time()
rf_model_default = RandomForestClassifier(random_state=42)
rf_model_default.fit(x_train, y_train)
rf_pred_default = rf_model_default.predict(x_test)
end_time = time.time()
print(f"默认模型训练与预测耗时: {end_time - start_time:.4f} 秒")
print("\n默认随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred_default))
print("默认随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred_default))
print("-" * 50)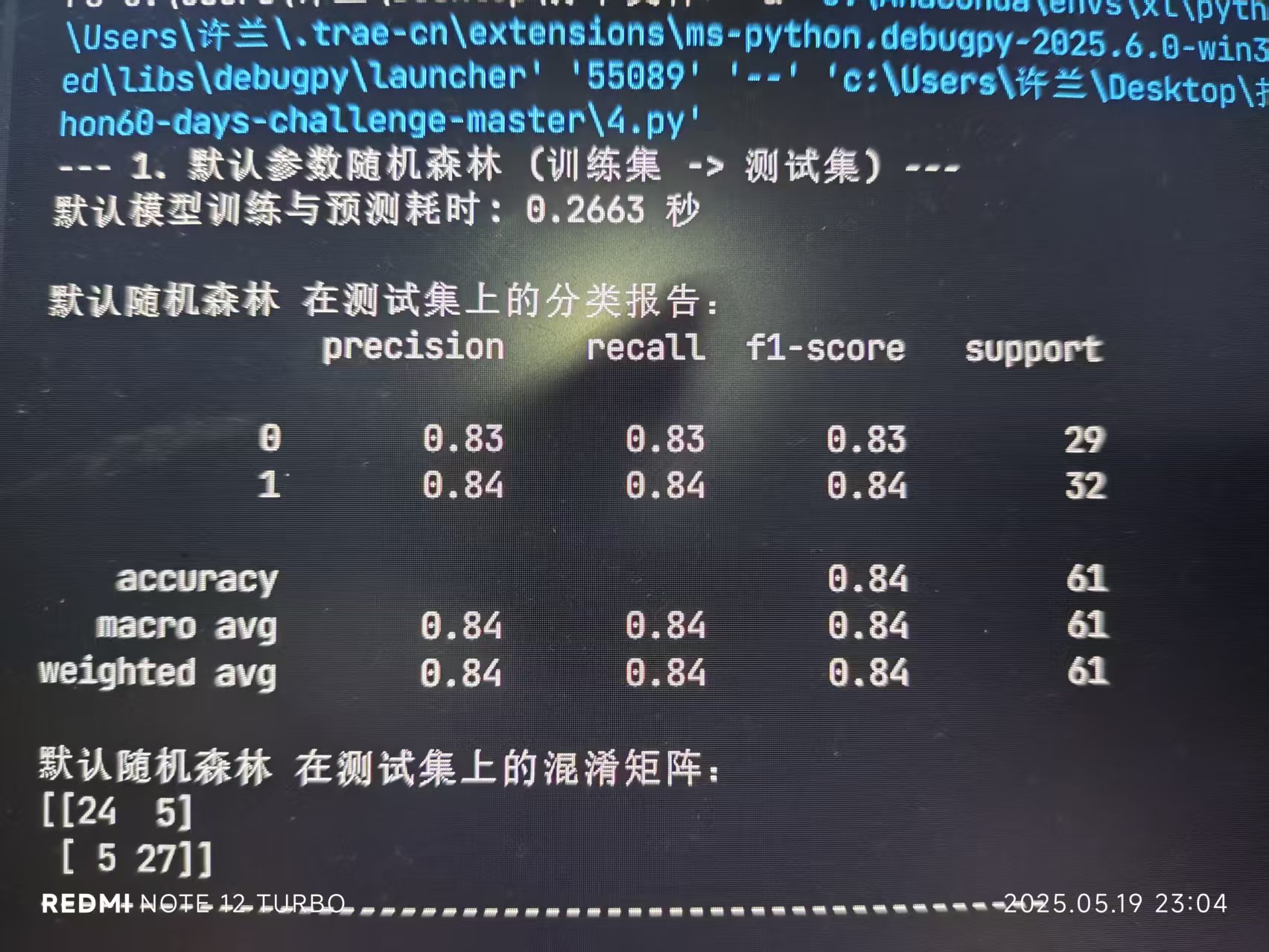

 

pca降维＋随机森林

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time
import numpy as np # 确保numpy导入# 假设 X_train, X_test, y_train, y_test 已经准备好了print(f"\n--- 2. PCA 降维 + 随机森林 (不使用 Pipeline) ---")# 步骤 1: 特征缩放
scaler_pca = StandardScaler()
x_train_scaled_pca = scaler_pca.fit_transform(x_train)
x_test_scaled_pca = scaler_pca.transform(x_test) # 使用在训练集上fit的scaler# 步骤 2: PCA降维
# 选择降到10维，或者你可以根据解释方差来选择，例如：
pca_expl = PCA(random_state=42)
pca_expl.fit(x_train_scaled_pca)
cumsum_variance = np.cumsum(pca_expl.explained_variance_ratio_)
n_components_to_keep_95_var = np.argmax(cumsum_variance >= 0.95) + 1
print(f"为了保留95%的方差，需要的主成分数量: {n_components_to_keep_95_var}")n_components_pca = 12
pca_manual = PCA(n_components=n_components_pca, random_state=42)x_train_pca = pca_manual.fit_transform(x_train_scaled_pca)
x_test_pca = pca_manual.transform(x_test_scaled_pca) # 使用在训练集上fit的pcaprint(f"PCA降维后，训练集形状: {x_train_pca.shape}, 测试集形状: {x_test_pca.shape}")
start_time_pca_manual = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_pca = RandomForestClassifier(random_state=42)
rf_model_pca.fit(x_train_pca, y_train)# 步骤 4: 在测试集上预测
rf_pred_pca_manual = rf_model_pca.predict(x_test_pca)
end_time_pca_manual = time.time()print(f"手动PCA降维后，训练与预测耗时: {end_time_pca_manual - start_time_pca_manual:.4f} 秒")print("\n手动 PCA + 随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred_pca_manual))
print("手动 PCA + 随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred_pca_manual))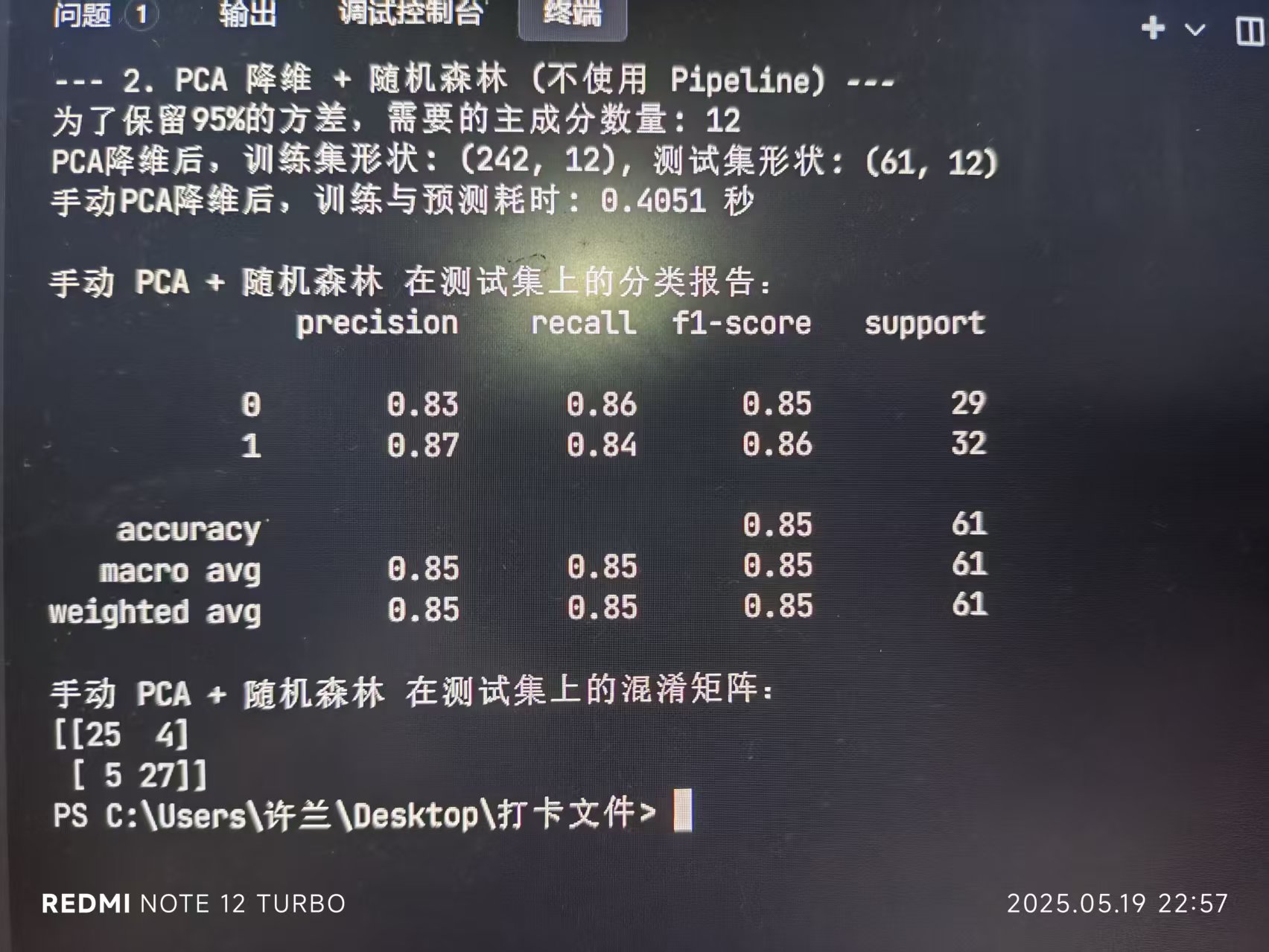

 

t-sne降维+随机森林

rom sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time
import numpy as np
import matplotlib.pyplot as plt # 用于可选的可视化
import seaborn as sns # 用于可选的可视化# 假设 X_train, X_test, y_train, y_test 已经准备好了
# 并且你的 X_train, X_test 是DataFrame或Numpy Arrayprint(f"\n--- 3. t-SNE 降维 + 随机森林  ---")
print("       标准 t-SNE 主要用于可视化，直接用于分类器输入可能效果不佳。")# 步骤 1: 特征缩放
scaler_tsne = StandardScaler()
x_train_scaled_tsne = scaler_tsne.fit_transform(x_train)
x_test_scaled_tsne = scaler_tsne.transform(x_test) # 使用在训练集上fit的scaler# 步骤 2: t-SNE 降维
# 我们将降维到与PCA相同的维度（例如10维）或者一个适合分类的较低维度。
# t-SNE通常用于2D/3D可视化，但也可以降到更高维度。
# 然而，降到与PCA一样的维度（比如10维）对于t-SNE来说可能不是其优势所在，
# 并且计算成本会显著增加，因为高维t-SNE的优化更困难。
# 为了与PCA的 n_components=10 对比，我们这里也尝试降到10维。
# 但请注意，这可能非常耗时，且效果不一定好。
# 通常如果用t-SNE做分类的预处理（不常见），可能会选择非常低的维度（如2或3）。# n_components_tsne = 10 # 与PCA的例子保持一致，但计算量会很大
n_components_tsne = 3   # 更典型的t-SNE用于分类的维度，如果想快速看到结果# 如果你想严格对比PCA的10维，可以将这里改为10，但会很慢# 对训练集进行 fit_transform
tsne_model_train = TSNE(n_components=n_components_tsne,perplexity=30,    # 常用的困惑度值n_iter=1000,      # 足够的迭代次数init='pca',       # 使用PCA初始化，通常更稳定learning_rate='auto', # 自动学习率 (sklearn >= 1.2)random_state=42,  # 保证结果可复现n_jobs=-1)        # 使用所有CPU核心
print("正在对训练集进行 t-SNE fit_transform...")
start_tsne_fit_train = time.time()
x_train_tsne = tsne_model_train.fit_transform(x_train_scaled_tsne)
end_tsne_fit_train = time.time()
print(f"训练集 t-SNE fit_transform 完成，耗时: {end_tsne_fit_train - start_tsne_fit_train:.2f} 秒")# 对测试集进行 fit_transform
# 再次强调：这是独立于训练集的变换
tsne_model_test = TSNE(n_components=n_components_tsne,perplexity=30,n_iter=1000,init='pca',learning_rate='auto',random_state=42, # 保持参数一致，但数据不同，结果也不同n_jobs=-1)
print("正在对测试集进行 t-SNE fit_transform...")
start_tsne_fit_test = time.time()
x_test_tsne = tsne_model_test.fit_transform(x_test_scaled_tsne) # 注意这里是 X_test_scaled_tsne
end_tsne_fit_test = time.time()
print(f"测试集 t-SNE fit_transform 完成，耗时: {end_tsne_fit_test - start_tsne_fit_test:.2f} 秒")print(f"t-SNE降维后，训练集形状: {x_train_tsne.shape}, 测试集形状: {x_test_tsne.shape}")start_time_tsne_rf = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_tsne = RandomForestClassifier(random_state=42)
rf_model_tsne.fit(x_train_tsne, y_train)# 步骤 4: 在测试集上预测
rf_pred_tsne_manual = rf_model_tsne.predict(x_test_tsne)
end_time_tsne_rf = time.time()print(f"t-SNE降维数据上，随机森林训练与预测耗时: {end_time_tsne_rf - start_time_tsne_rf:.4f} 秒")
total_tsne_time = (end_tsne_fit_train - start_tsne_fit_train) + \(end_tsne_fit_test - start_tsne_fit_test) + \(end_time_tsne_rf - start_time_tsne_rf)
print(f"t-SNE 总耗时 (包括两次fit_transform和RF): {total_tsne_time:.2f} 秒")print("\n手动 t-SNE + 随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred_tsne_manual))
print("手动 t-SNE + 随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred_tsne_manual))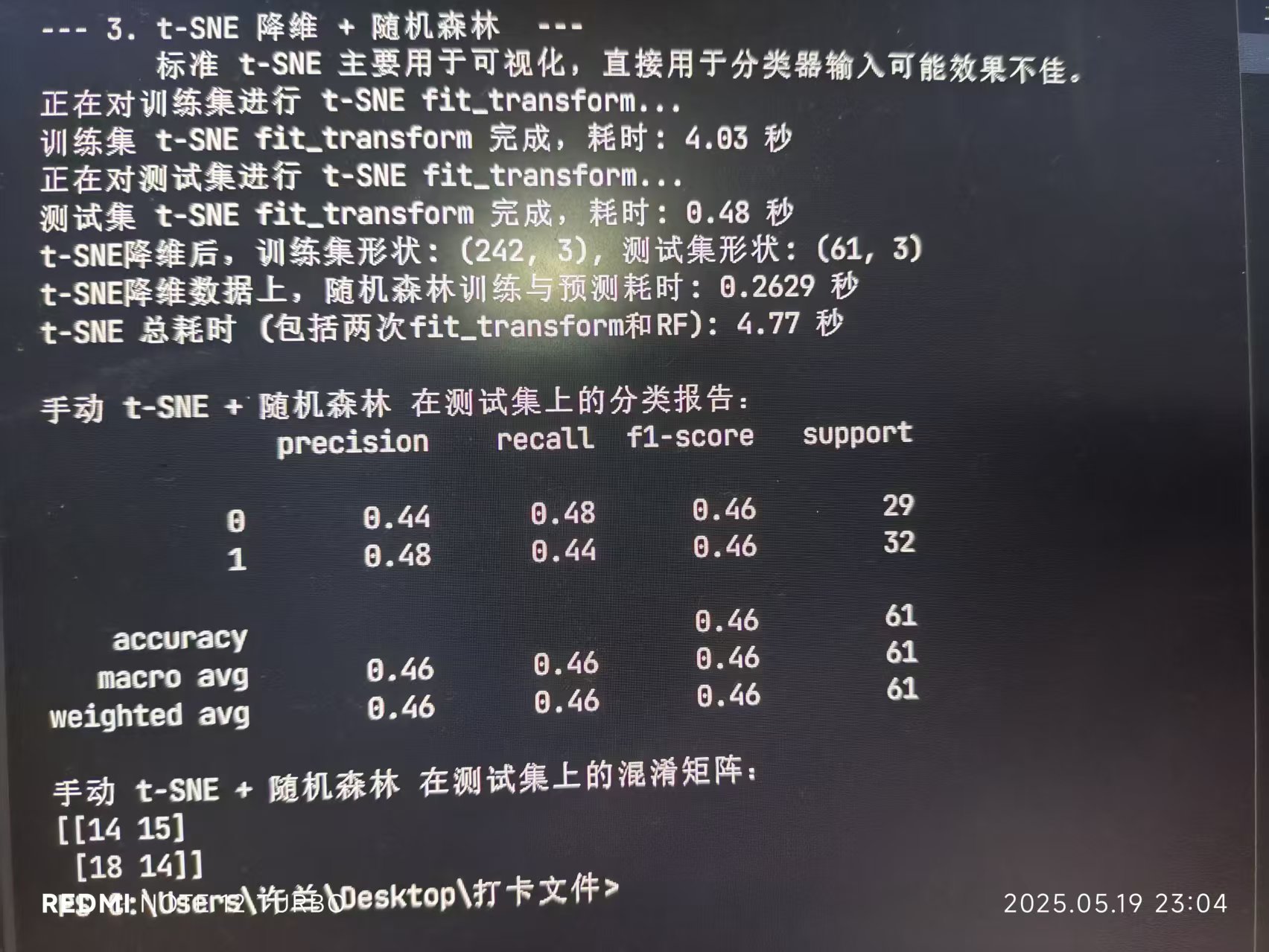

 

@浙大疏锦行 

 

相关文章：

打卡第二十二天

知识点回顾： LDA线性判别PCA主成分分析t-SNE降维 还有一些其他的降维方式，也就是最重要的词向量的加工，我们未来再说。 作业： 自由作业：探索下什么时候用到降维？降维的主要应用？或者让AI给你出…...

编程日记 2025/7/19 4:51:46

【Unity 2023 新版InputSystem系统】新版InputSystem 如何进行人物移动（包括配置、代码详细实现过程）

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言一、InputSystem配置二、GameInput 游戏输入脚本1.实现思路2.完整代码三、Player 游戏人物移动脚本1.实现思路2.完整代码四、场景脚本设置1.组件设置五、问题解决1.人物一直下落2.人物跳跃时，…...

编程日记 2025/7/15 23:42:20

Python实现的在线词典学习工具

Python实现的在线词典学习工具 源码最初来自网络，根据实际情况进行了修改。 主要功能： 单词查询 通过Bing词典在线获取单词释义（正则提取网页meta描述），支持回车键快速查询 内置网络请求重试和异常处理机制 在线网页…...

编程日记 2025/7/16 2:08:56

软考 系统架构设计师系列知识点之杂项集萃（63）

接前一篇文章：软考 系统架构设计师系列知识点之杂项集萃（62） 第102题 以下关于系统性能评估方法的描述，错误的是（）。 A. 指令执行速度法常用每秒百万次指令运算（MIPS）评估系统性能…...

编程日记 2025/7/16 18:35:13

python重庆旅游系统-旅游攻略

目录 技术栈介绍具体实现截图系统设计研究方法：设计步骤设计流程核心代码部分展示研究方法详细视频演示试验方案论文大纲源码获取/详细视频演示 技术栈介绍 Django-SpringBoot-php-Node.js-flask 本课题的研究方法和研究步骤基本合理，难度适中&#xf…...

编程日记 2025/7/15 20:10:53

如何使用GIT管理项目代码

介绍 ​ Git是目前世界上最流行甚至最好的开源分布式版本控制系统，不论是很小的项目还是很大的项目，它都能有效并且高效的处理项目版本管理，初衷是为了帮助管理linux内核代码而开发的一个开放源码的版本控制软件。 GIT常用分支名称 分支分…...

编程日记 2025/7/19 4:42:39

Android 11.0 动画缩放默认值改为0.5的功能实现

1.前言 在11.0的系统rom定制化开发中，在关于设置动画的时候，系统有相关参数要求，设置默认的 动画缩放默认值等功能，来实现相关功能，接下来分析下相关的动画默认缩放值的设置功能实现 2.动画缩放默认值改为0.5的功能实现的核心类 frameworks/base/packages/SettingsProv…...

编程日记 2025/7/19 4:50:45

第35周Zookkeeper+Dubbo 面试题精讲

面试题精讲 一、算法面试答题思路 理解思路的重要性：算法面试比基础面试更复杂，需先想清楚思路，与面试官沟通确认题目条件（如数据范围、是否包含负数/零等），这有助于理清解题思路并展示技术实力。变量命名清晰：算法中变量命名要明确含义和范围，避免使用模糊的变量名，…...

编程日记 2025/7/18 15:16:26

Mergekit——任务向量合并算法Ties解析

Mergekit——高频合并算法 TIES解析 Ties背景Ties 核心思想具体流程总结 mergekit项目地址 Mergekit提供模型合并方法可以概况为三大类：基本线性加权、基于球面插值、基于任务向量，今天我们来刷下基于任务向量的ties合并方法，熟悉原理和代码。…...

编程日记 2025/7/16 17:15:08

初识 Redis

什么是 Redis？ 在 Redis 官网中有介绍， Redis 就是一个存储空间，只不过这个存储空间是在内存上的，这也就代表存储在 Redis 中的数据访问起来会非常快，但也会有一个弊端，也就是内存资源是非常少的&#xff…...

编程日记 2025/7/17 1:08:05

python打卡训练营打卡记录day30

一、导入官方库 我们复盘下学习python的逻辑，所谓学习python就是学习python常见的基础语法学习你所处理任务需要用到的第三方库。 1.1标准导入：导入整个库 这是最基本也是最常见的导入方式，直接使用import语句。 # 方式1：导入整…...

编程日记 2025/7/15 17:21:30

FART 主动调用组件设计和源码分析

版权归作者所有，如有转发，请注明文章出处：https://cyrus-studio.github.io/blog/ 现有脱壳方法存在的问题 脱壳粒度集中在 DexFile 整体，当前对 apk 保护的粒度在函数粒度，这就导致了脱壳与加固的不对等，无…...

编程日记 2025/7/15 16:51:02

windows使用ollama部署deepseek及qwen

ollama 参考文档 ollama 官方文档 GitHub仓库 基础环境： NVIDIA 1660TI 6G 下载 ollma是一款开源工具，支持在本地计算机（无需联网）快速部署和运行大型语言模型（LLM），如 LLaMA、Mistral、G…...

编程日记 2025/7/16 0:02:48

【11408学习记录】考研英语辞职信写作三步法：真题精讲+妙句活用+范文模板

应聘信 英语写作2005年考研英语真题小作文写作思路第一段第二段妙句7 9妙句11补充3补充4 第三段 妙句成文 每日一句词汇第一步：找谓语第二步：断句第三步：简化主句原因状语从句 英语 写作 2005年考研英语真题小作文 Directions:​​ Two m…...

编程日记 2025/7/16 5:06:59

湖北理元理律师事务所：债务优化如何实现“减负不降质”？

债务压力下，如何在保障基本生活品质的同时科学规划还款，是许多债务人面临的现实难题。湖北理元理律师事务所通过多年实务经验，总结出一套“法律财务心理”的复合型解决方案。本文基于公开案例与法律框架，解析其服务逻辑中的可借鉴…...

编程日记 2025/7/15 21:57:48

python fastapi + react, 写一个图片 app

1. 起因， 目的: 上厕所的时候，想用手机查看电脑上的图片，但是又不想点击下载。此app 应运而生。 2. 先看效果 单击图片，能放大图片 3. 过程: 过程很枯燥。有时候， 有一堆新的想法。 但是做起来太麻烦，…...

编程日记 2025/7/16 21:30:31

Golang的Web应用架构设计

# Golang的Web应用架构设计 介绍 是一种快速、高效、可靠的编程语言，它在Web应用开发中越来越受欢迎。Golang的Web应用架构设计通常包括前端、后端和数据库三个部分。在本篇文章中，我们将详细介绍Golang的Web应用架构设计及其组成部分。 前端 在Golang的…...

编程日记 2025/7/16 12:34:18

软件设计师“UML”真题考点分析——求三连

一、考点分值占比与趋势分析 综合知识题分值统计表 年份考题数量分值分值占比考察重点2018222.67%类图关系、序列图消息流2019334.00%对象图特征、部署图辨析2020222.67%组件图特性、泛化关系2021334.00%聚合/组合区别、交互图应用2022222.67%用例图参与者、状态图转换202344…...

编程日记 2025/7/16 1:40:40

Nginx端口telnet不通排查指南

nginx已经配置server及端口20002，telnet不通：telnet 127.0.0.1 20002 Trying 127.0.0.1... telnet: connect to address 127.0.0.1: Connection refused 一、检查 systemctl status nginx.service nginx: [emerg] bind() to 0.0.0.0:20002 failed (13…...

编程日记 2025/7/1 9:22:24

C++ 函数对象、仿函数与 Lambda 表达式详解

C 函数对象、仿函数与 Lambda 表达式详解 在 C 中，函数对象（Function Object）、仿函数（Functor） 和 Lambda 表达式 是三种实现可调用行为的技术，它们在功能上类似，但语法和适用场景有所不同。 …...

编程日记 2025/7/18 4:49:02

More Effective C++：改善编程与设计（下）

目录 条款19:了解临时对象的来源 条款20:协助完成“返回值优化” 条款21:利用重载技术避免隐式类型转换 条款22:考虑以操作符复合形式（op）取代其独身形式（op） 条款23:考虑使用其他程序库 条款24:了解virtual functions、mul…...

编程日记 2025/7/15 22:13:13

C++：判断闰年

【描述】 判断某年是否是闰年。 【输入】 输入只有一行&#xff0c;包含一个整数a(0 < a < 3000) 【输出】 一行&#xff0c;如果公元a年是闰年输出Y&#xff0c;否则输出N 【样例输入】 2006 【样例输出】 N 【提示】 公历纪年法中&#xff0c;能被4整除的大多是闰年&am…...

编程日记 2025/7/16 5:01:23

C+++STL（一）

/ 文章目录 模版C作为静态类型语言宏可以摆脱数据类型的限制利用宏构建通用函数框架 函数模版函数模版的定义函数模版的使用函数模版的分析实例化函数模版的条件 函数模版扩展二次编译隐式推断类型实参函数模版的重载 bilibili 学习网址&#xff1a;https://www.bilibili.com/…...

编程日记 2025/7/16 19:28:10

C 语言学习笔记（函数2）

内容提要 函数 函数的调用函数的声明函数的嵌套关系函数的递归调用数组做函数参数 函数 函数的调用 调用方式 ①函数语句&#xff1a; test (); //对于无返回值的函数&#xff0c;直接调用 int res max(2,4); //对于有返回值的函数&#xff0c;一般需要在主调函…...

编程日记 2025/7/16 20:11:19

Spring的后置处理器是干什么用的？扩展点又是什么？

Spring 的后置处理器和扩展点是其框架设计的核心机制&#xff0c;它们为开发者提供了灵活的扩展能力&#xff0c;允许在 Bean 的生命周期和容器初始化过程中注入自定义逻辑。 1. 后置处理器&#xff08;Post Processors&#xff09; 后置处理器是 Spring 中用于干预 Bean 生命…...

编程日记 2025/7/17 21:17:30

Java大数据机器学习模型在金融衍生品风险建模中的创新实践

摘要 本文深入探讨Java技术栈在大数据与机器学习领域的独特优势&#xff0c;及其在金融衍生品风险建模中的突破性应用。通过分析分布式计算框架与机器学习库的整合方案&#xff0c;揭示Java在构建复杂金融风险模型时的技术可行性。结合信用违约互换&#xff08;CDS&#xff09…...

编程日记 2025/7/18 9:59:21

leetcode3403. 从盒子中找出字典序最大的字符串 I-medium

1 题目&#xff1a;从盒子中找出字典序最大的字符串 I 官方标定难度&#xff1a; 给你一个字符串 word 和一个整数 numFriends。 Alice 正在为她的 numFriends 位朋友组织一个游戏。游戏分为多个回合&#xff0c;在每一回合中&#xff1a; word 被分割成 numFriends 个 非空…...

编程日记 2025/7/18 1:18:45

Effective C++阅读笔记（item 1-4)

文章目录 理解模板类型推导理解auto类型推导理解decltype学会查看类型推导结果 理解模板类型推导 c的auto特性是建立在模板类型推到的基础上。坏消息是当模板类型推导规则应用于auto环境时&#xff0c;有时不如应用于template时那么直观。我们可能很自然的期望T和传递进函数的…...

编程日记 2025/7/15 22:44:48

python自学笔记4 控制结构

条件语句 略 循环语句 略 range函数 enumerate() 函数 可以将一个可迭代对象转换为一个由索引和元素组成的枚举对象。 索引的起始编号是0&#xff0c;也可以传入第二参数来指定其起始编号 zip函数 打包范围以两者最短的长度为准 以两者较长的长度为准的函数为itertool…...

编程日记 2025/7/16 23:55:10

VTK|显示三维图像的二维切片

参考&#xff1a; VTK显示三维图像的二维切片 文章目录 实现类头文件实现类源文件如何调用项目git链接 以中心点坐标横切面 实现类头文件 /*** file MeshSliceController.h* brief 该头文件定义了 MeshSliceController 类&#xff0c;用于显示切面图。* details 该类负责处理与…...

编程日记 2025/7/16 13:24:39

day 30

模块和库的导入 导入官方库 标准导入&#xff1a;导入整个库 直接使用import语句 # 方式1&#xff1a;导入整个模块 import mathprint("方式1&#xff1a;使用 import math") print(f"圆周率π的值&#xff1a;{math.pi}") print(f"2的平方根&#xf…...

编程日记 2025/7/1 10:39:01

Linux云计算训练营笔记day11【Linux CentOS7（cat、less、head、tail、lscpu、lsblk、hostname、vim、which、mount、alias）】

Linux云计算 云计算是一种服务&#xff0c;是通过互联网按需提供计算资源的服务模式 程序员写代码的&#xff0c;部署上线项目 买服务器(一台24小时不关机的电脑&#xff0c;为客户端提供服务) 20万 买更多的服务器 Linux(命令) windows(图形化) 就业岗位: 云计算工程师 li…...

编程日记 2025/7/18 14:07:56

使用Python和FastAPI构建网站爬虫：Oncolo医疗文章抓取实战

使用Python和FastAPI构建网站爬虫&#xff1a;Oncolo医疗文章抓取实战 前言项目概述技术栈代码分析1. 导入必要的库2. 初始化FastAPI应用3. 定义请求模型4. 核心爬虫功能4.1 URL验证和准备4.2 设置HTTP请求4.3 发送请求和解析HTML4.4 提取文章内容4.5 保存结果和返回数据 5. AP…...

编程日记 2025/7/1 10:38:58

光纤克尔非线性效应及其在光通信系统中的补偿教程-3.2 克尔效应

需要结合上一期的文章&#xff0c;光纤克尔非线性效应及其在光通信系统中的补偿教程-3.1 非线性极化性 光纤中的非线性效应源于三阶感性 χ ( 3 ) \chi^{(3)} χ(3)。 光纤中非线性效应的主要来源之一是由 χ ( 3 ) \chi^{(3)} χ(3)引起的非线性折射&#xff0c;即克尔效应&a…...

编程日记 2025/7/17 16:02:15

【Tools】VMware Workstation 17.6 Pro安装教程

00. 目录 文章目录 00. 目录01. VMware Workstation 17.6简介02. VMware Workstation 17.6新功能03. VMware Workstation 17.6特性04. VMware Workstation 17.6下载05. VMware Workstation 17.6安装06. VMware Fusion 和 Workstation免费07. 附录 01. VMware Workstation 17.6简…...

编程日记 2025/7/17 12:07:00

Unity10分钟回顾指南

&#x1f3ae; Unity10分钟回顾指南 欢迎踏上Unity场景创作之旅&#xff01;本教程将带你从零开始&#xff0c;循序渐进地掌握Unity场景制作的全部技能。无论你是游戏开发爱好者还是专业开发者&#xff0c;这份指南都将成为你的得力助手。 第一章&#xff1a;Unity基础认知 1.…...

编程日记 2025/7/16 17:46:54

SeleniumBase - 多合一浏览器自动化框架

手动编写Selenium脚本&#xff0c;繁琐且常遇“掉坑”&#xff1f;SeleniumBase来救场&#xff01;这款基于Selenium的Python框架集测试、爬虫、RPA于一体&#xff0c;支持多浏览器、并行测试、CAPTCHA绕过和智能等待&#xff0c;堪称Web自动化的“瑞士军刀”。不少行业大佬盛赞…...

编程日记 2025/7/18 19:45:14

【人工智能导论】第2.3章知识表示、确定性推理

1、李明的父亲是教师&#xff0c;用谓词逻辑可以表示为Teacher&#xff08;father&#xff08;Liming&#xff09;&#xff09;这里father&#xff08;Liming&#xff09;是&#xff08; &#xff09; A、常量 LIMING B、变元 X未知的可取多个值的对象 C、函数 X的父亲 D、一元…...

编程日记 2025/7/1 10:38:47

【QT】一个界面中嵌入其它界面（一）

在 Qt 中嵌入其他界面通常可以通过以下几种方式实现。以下是详细的步骤说明和示例代码&#xff1a; 方法 1&#xff1a;直接通过布局嵌入子部件 如果目标界面是 QWidget 的子类&#xff0c;可以直接将其添加到父窗口的布局中。 步骤&#xff1a; 创建子界面类&#xff1a; //…...

编程日记 2025/7/1 10:38:45

[学习]POSIX消息队列的原理与案例分析（完整示例代码）

POSIX消息队列的原理与案例分析 文章目录 POSIX消息队列的原理与案例分析摘要关键词一、引言1.1 研究背景与意义1.2 国内外研究现状1.3 研究内容与方法 二、POSIX消息队列的基本原理2.1 消息队列概述2.2 POSIX消息队列的特性2.2 POSIX消息队列的特性2.3 POSIX消息队列的内部机制…...

编程日记 2025/7/17 1:26:41

IDC数据中心动力环境监控系统解决方案

文档围绕 IDC 数据中心动力环境监控系统解决方案展开，先介绍数据中心分级，包括国家规范的 A/B/C 级和美国 TIA-942 标准的 Tier1-Tier4 级，强调动环监控对数据中心的重要性。接着阐述系统架构，涵盖底端设备层、采集层、接入层、服务层、应用层，具备数据采集、分析、可视化…...

编程日记 2025/7/17 8:21:23

WebSphere Application Server（WAS）8.5.5教程第五讲

续前篇&#xff01; 一、Web 应用部署与类加载策略 Web 应用部署与类加载策略是 WebSphere Application Server&#xff08;WAS&#xff09;日常管理的核心部分&#xff0c;尤其对运行大型企业级 Java 应用&#xff08;如 BAW&#xff09;非常关键。本讲将分两部分讲解&#…...

编程日记 2025/7/17 1:28:06

Golang中的runtime.LockOSThread 和 runtime.UnlockOSThread

在runtime中有runtime.LockOSThread 和 runtime.UnlockOSThread 两个函数&#xff0c;这两个函数有什么作用呢&#xff1f;我们看一下标准库中对它们的解释。 runtime.LockOSThread // LockOSThread wires the calling goroutine to its current operating system thread. // T…...

编程日记 2025/7/18 8:34:53

计算圆周率 (python)

使用模特卡罗方法&#xff08;模拟法&#xff09;&#xff0c;模拟撒点100000次&#xff0c;计算圆周率π 输入格式: 一个整数&#xff0c;表示随机数种子 输出格式: 计算的π值&#xff0c;结果小数点后保留5位数字 输入样例: 在这里给出一组输入。例如&#xff1a; 10…...

编程日记 2025/7/17 6:07:43

机器学习EM算法原理及推导

在机器学习与统计推断中&#xff0c;我们经常会遇到“缺失数据”或“潜在变量”&#xff08;latent variables&#xff09;的情形&#xff1a;样本并非完全可观测&#xff0c;而部分信息被隐藏或丢失。这种情况下&#xff0c;直接对观测数据做极大似然估计&#xff08;Maximum …...

编程日记 2025/7/1 10:38:31

Linux项目部署全攻略：从环境搭建到前后端部署实战

Linux项目部署全攻略&#xff1a;从环境搭建到前后端部署实战 注&#xff1a;根据黑马程序员javawebAI视频课程总结&#xff1a; 视频地址 详细讲义地址 一、Linux基础入门&#xff1a;为什么选择Linux&#xff1f; 要成为一名Java开发工程师&#xff0c;掌握Linux是企业级…...

编程日记 2025/7/18 21:24:09

人工智能重塑医疗健康：从辅助诊断到个性化治疗的全方位变革

人工智能正在以前所未有的速度改变着医疗健康领域&#xff0c;从影像诊断到药物研发&#xff0c;从医院管理到远程医疗&#xff0c;AI 技术已渗透到医疗服务的各个环节。本文将深入探讨人工智能如何赋能医疗健康产业&#xff0c;分析其在医学影像、临床决策、药物研发、个性化医…...

编程日记 2025/7/16 19:54:35

ubuntu系统 | dify+ollama+deepseek搭建本地应用

1、安装 Ollama 下载并安装 Ollama (llm) wangqiangwangqiang:~$ curl -fsSL https://ollama.ai/install.sh | bash >>> Installing ollama to /usr/local >>> Downloading Linux amd64 bundle0.3% curl -fsSL https://ollama.ai/install.sh &#xff08;下…...

编程日记 2025/7/18 7:16:32

NHANES最新指标推荐：C-DII

文章题目&#xff1a;Non-linear relationship between the childrens dietary inflammatory index and asthma risk: identifying a critical inflection point in US children and adolescents DOI&#xff1a;10.3389/fnut.2025.1538378 中文标题&#xff1a;儿童饮食炎症指…...

编程日记 2025/7/1 10:38:22

【PhysUnits】4.4 零类型(Z0)及其算术运算(zero.rs)

一、源码 该代码定义了一个类型系统中的零类型Z0&#xff0c;并为其实现了基本的算术运算&#xff08;加法、减法、乘法、除法&#xff09;。这是一个典型的类型级编程示例&#xff0c;使用Rust的类型系统在编译期进行数学运算。 //! 零类型(Z0)及其算术运算实现 //! //! 本…...

编程日记 2025/7/17 10:54:28