当前位置：首页 > news >正文

【人工智能导论】第2.3章知识表示、确定性推理

news 来源：原创 2025/7/19 7:04:58

1、李明的父亲是教师，用谓词逻辑可以表示为Teacher（father（Liming））这里father（Liming）是（）
A、常量 LIMING
B、变元 X未知的可取多个值的对象
C、函数 X的父亲
D、一元谓词 x是老师

2、定义谓词Like(x,y) 表示x喜欢y，个体域为全体人类，以下表示“每个人都有喜欢的人”含义的谓词公式是( )B

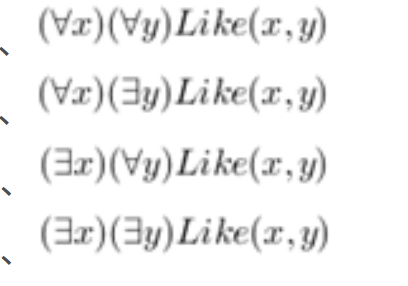
3、对于谓词公式，以下说法错误的是（ C）
A、上述公式中的所有 y 是自由变元
B、P(x, y) 中的 x 是约束变元
C、R(x, y) 中的 x 是约束变元
D、Q(x, y) 中的 x 是约束变元

约束变元：量词（如全称量词 ∀ 或存在量词 ∃）所限定的变量

自由变元：没有被量词限定

4、不适合用产生式表示法表示的知识是（ C）
A、由许多相对独立的知识元组成的领域知识
B、可以表示为一系列相对独立的求解问题的操作
C、具有结构关系的知识
D、具有经验性及不确定性的知识

产生式规则（Production Rules）：形式为 "IF 条件 THEN 结论"。基于规则的知识表示

产生式表示法：适合表示独立的、经验性、不确定性的知识，尤其是由许多相对独立的知识元组成的领域知识，或者可以分解为一系列相对独立操作的问题。

对于具有复杂结构关系的知识，产生式表示法不太适用。--框架表示法

5、下列不是框架表示法特点的是（D ）
A、结构性
B、模块性
C、继承性
D、自然性

框架表示法通过构建框架（Frame）来表示个体（对象）的知识。每个框架就像是一个数据结构，里面包含了与某个对象相关的属性、行为和关系。

6、假设我们定义了以下谓词： Study(x) x肯学习，Lucky(x) x是幸运的那么下列哪个谓词公式对于以下知识的表示是正确的？ “小张不肯学习但他是幸运的”
A、﹁Study(zhang)∧Lucky(zhang)
B、﹁(Study(zhang)∧Lucky(zhang))
C、﹁(Study(zhang)∨Lucky(zhang))
D、﹁Study(zhang)∨Lucky(zhang)

但--用析取还是合取？A但B可以理解为“A且B”，即 A 和 B 同时成立。﹁Study(zhang)∧Lucky(zhang)

关系	含义	举例

析取（∨）

或：表示至少一个为真，两个条件之间是“或”的关系。

A ∨ B（A或B成立即可）

与（∧）

与：表示两个条件都为真，两个条件之间是“并且”的关系。

A ∧ B（A和B都成立）

7、以下哪一项属于产生式？A
A、编译原理中的文法
B、数据库中的SQL语句
C、程序设计中的IF语句用于控制执行流程
D、操作系统中的作业调度算法

产生式是定义语言结构和语法的规则，用来推导和生成符号

if then 基于规则的知识表示

它的基本形式是：
左侧 → 右侧，描述从一个符号生成另一个符号。是语法规则的一部分

8、把一组产生式放在一起，让他们互相配合，协同作用，一个产生式生成的结论可以供另一个产生式作为已知事实使用，以求得问题的解，这样的系统称为产生式系统。一般来说，一个产生式系统由( BD)组成。
A、解释器
B、规则库
C、综合数据库
D、推理机

产生式系统:

规则库（Rule Base）：包含所有产生式规则，有前提和结论组成

工作存储区（Working Memory）：存储当前的已知事实

推理机（Inference Engine）：根据规则和事实进行推理

参考答案：见本章说明

9、一阶谓词逻辑中的个体可以是( )
A、常量
B、变元
C、函数
D、一元谓词

10、一阶谓词逻辑表示法的优点有（）
A、自然性
B、精确性
C、严密性符合逻辑公理和推理规则
D、易实现

11、以下哪些是谓词公式？AC
A、P(x)
B、﹁P(x)∧Q(x)←R(x)
C、P(x)→Q(x)
D、P(x)+Q(X)→Q(x)

谓词公式包括：谓词，变元xy，常量jun，量词∀, ∃，逻辑连接词如 ∧, ∨, →, ¬

12、一个命题不能同时既为真又为假，但可以在一种条件下为真，在另一种条件为假。

对

13、命题逻辑可以把所描述的事物的结构及其逻辑特征反映出来，也能把不同事物间的共同特征表述出来。

对

14、一阶谓词逻辑表示法可以表示不确定的知识。

错

15、框架表示法不能表示具有因果关系的知识。

错框架表示法不仅能够表示对象的属性和关系，还可以通过设计槽和子框架的关系来表示因果关系

16、产生式系统求解问题的过程是一个反复进行“匹配–冲突消解–执行”的过程。

对 产生式系统通过匹配（matching）规则与当前事实、冲突消解（conflict resolution）来选择适用的规则，并执行（execution）这些规则以推导新事实。

17、框架的槽值或侧面值不能是另一个框架的名字。

错框架是模块性，继承性的

18、产生式有固定的格式，每一条产生式规则都由前提与结论（操作）两部分组成。

对

19、论域是由所讨论对象的全体构成的非空集合。

对论域指的是所有个体的集合

第3章　确定性推理方法

1、由一般性知识推出适合于某一具体情况的结论的推理是？
A、演绎推理
B、归纳推理
C、默认推理
D、单调推理

演绎推理：用一般性知识推导出具体结论的过程

归纳推理（B）是从具体的观察或实例推导出一般性结论的过程。

默认推理（C）是指在没有充分证据时，根据已知信息作出的合理假设。

单调推理（D）是指推理过程中不会引入矛盾的推理方式。

2、若C1=P(x) ∨Q(x)，C2=┐P(a) ∨R(y)，则C1和C2的归结式R（C1，C2）=( )
A、P(x) ∨Q(x)
B、P(a) ∨Q(x)
C、Q(x) ∨R(y)
D、Q(a) ∨R(y)

归结？？

3、在公式中 ∀y∃x p(x,y))，存在量词是在全称量词的辖域内，我们允许所存在的x可能依赖于y值。令这种依赖关系明显地由函数所定义，把每个y值映射到存在的那个x。这种函数叫做（）
A、依赖函数
B、Skolem函数
C、决定函数
D、多元函数

参考答案：见本章说明

4、P→Q Q→R => P→R 该永真蕴含式属于（）
A、假言推理
B、拒取式推理
C、假言三段论
D、全称固化

假言推理：

如果P，则Q（P → Q）

P为真（P）

因此Q为真（Q）

拒取式推理：后错推前面

如果P，则Q（P → Q）

Q为假（¬Q）

因此P为假（¬P）

假言三段论

如果P，则Q（P → Q）

如果Q，则R（Q → R）

因此，如果P，则R（P → R）

全称固化：

5、谓词逻辑下，子句 C1=L∨C1’, C2= ┐L∨C2’, 若σ是互补文字的最一般合一代换，则其归结式 C12=（）
A、C1’σ∨C2’σ
B、C1’∨C2’
C、C1’σ∧C2’σ
D、C1’∧C2’

参考答案：见本章说明

6、以下属于不合法代换的有( )
A、{f(a)/b}
B、{x/y,f(y)/x}
C、{a/y,f(y)/x}
D、{f(x)/y,x/z}

参考答案：见本章说明

7、以下推理错误的是（）
A、P,P→Q => Q 假言推理
B、┓Q,P→Q => ┓P 拒取式
C、Q,P→Q => P
D、┓P,P→Q => ┓Q

参考答案：见本章说明

8、从初始证据出发，按某种策略不断运用知识库中的已知知识，逐步推出结论的过程称为推理。

正确。推理是从已知事实出发，根据推理规则逐步得出结论的过程。

9、任何文字的合取式称为子句。

错

子句是多个文字通过析取符号（OR）连接在一起的。

P(x) ∨ Q(x, y) 就是一个子句，其中包含两个文字：P(x) 和 Q(x, y)。

10、空子句是可以满足的。

错，空子句表示逻辑矛盾，它是一个无法满足的子句

11、谓词公式不可满足的充要条件是其子句集不可满足。

正确。如果谓词公式不可满足，那么它的子句集也不可满足。

归结：在子句集找到互补文字，并消去，得到新的子句。直到得到一个空子句（逻辑冲突）或不能再归结。

归结的目标是判断公式/原子句集是否可满足

通过归结得到空子句，证明公式/是不可满足的。

12、对于一阶谓词逻辑，若子句集是不可满足的，则必存在一个从该子句集到空子句的归结演绎。

对，如果子句集是不可满足的，通过归结方法我们可以推导出一个空子句，即表示矛盾或无法满足的情况。

13、对于一阶谓词逻辑，如果没有归结出空子句，则说明原谓词公式是不可满足的。

错，没有归结出空子句不代表原子句集可满足

第3章 确定性推理方法

归结：在子句集找到互补文字，并消去，得到新的子句。直到得到一个空子句（逻辑冲突）或不能再归结。

相关文章：

第3章　确定性推理方法