buuctf RSA之旅
BUUCTF-RSA的成长之路
- rsarsa
- RSA1
- RSA3
- RSA2
- RSA
- RSAROLL
- Dangerous RSA
- [GUET-CTF2019]BabyRSA
- rsa2
- RSA5
- [NCTF2019]childRSA
- [HDCTF2019]bbbbbbrsa
- RSA4
- [BJDCTF2020]rsa_output
- [BJDCTF2020]RSA
- [WUSTCTF2020]babyrsa
- [ACTF新生赛2020]crypto-rsa0
- [ACTF新生赛2020]crypto-rsa3
- [GWCTF 2019]BabyRSA
- SameMod
- [BJDCTF2020]easyrsa
- [AFCTF2018]你能看出这是什么加密么
- [NCTF2019]babyRSA
- 可怜的RSAimport gmpy2
- [RoarCTF2019]babyRSA
- [RoarCTF2019]RSA
- [网鼎杯 2020 青龙组]you_raise_me_up
- RSA & what
- [NPUCTF2020]EzRSA
- [MRCTF2020]babyRSA
- [WUSTCTF2020]情书
- [WUSTCTF2020]dp_leaking_1s_very_d@angerous
- [HDCTF2019]together
感谢轩禹!!!!!关注了风二西的b站哈哈,宝藏博主
rsarsa
熟悉轩禹软件的应用
1.(p,q)的形式填入题目中的p,q

2.计算N左上角计算模数N和phiN

3.在Private(D)格子出,右键计算私钥D

4.将题目中密文C填入对应格子中
5.在明文(M)处右键计算M


RSA1
轩禹一把梭

右键,点击运行后出结果
太好使了!!!!!!!
RSA3
简单看了一下题应该也是脚本直接出的
轩禹一把梭
在IDE选项中选择【脚本】-【基础脚本】-【共模攻击】,对应修改参数。flag{49d91077a1abcb14f1a9d546c80be9ef}

RSA2
dp泄露
轩禹一把梭
flag{wow_leaking_dp_breaks_rsa?_98924743502}

RSA
打开为两个文件

意思是使用pub.key(公钥)解开flag.enc
使用轩禹分解公钥得到模数N和指数E

由于N=p*q,使用轩禹进行分解
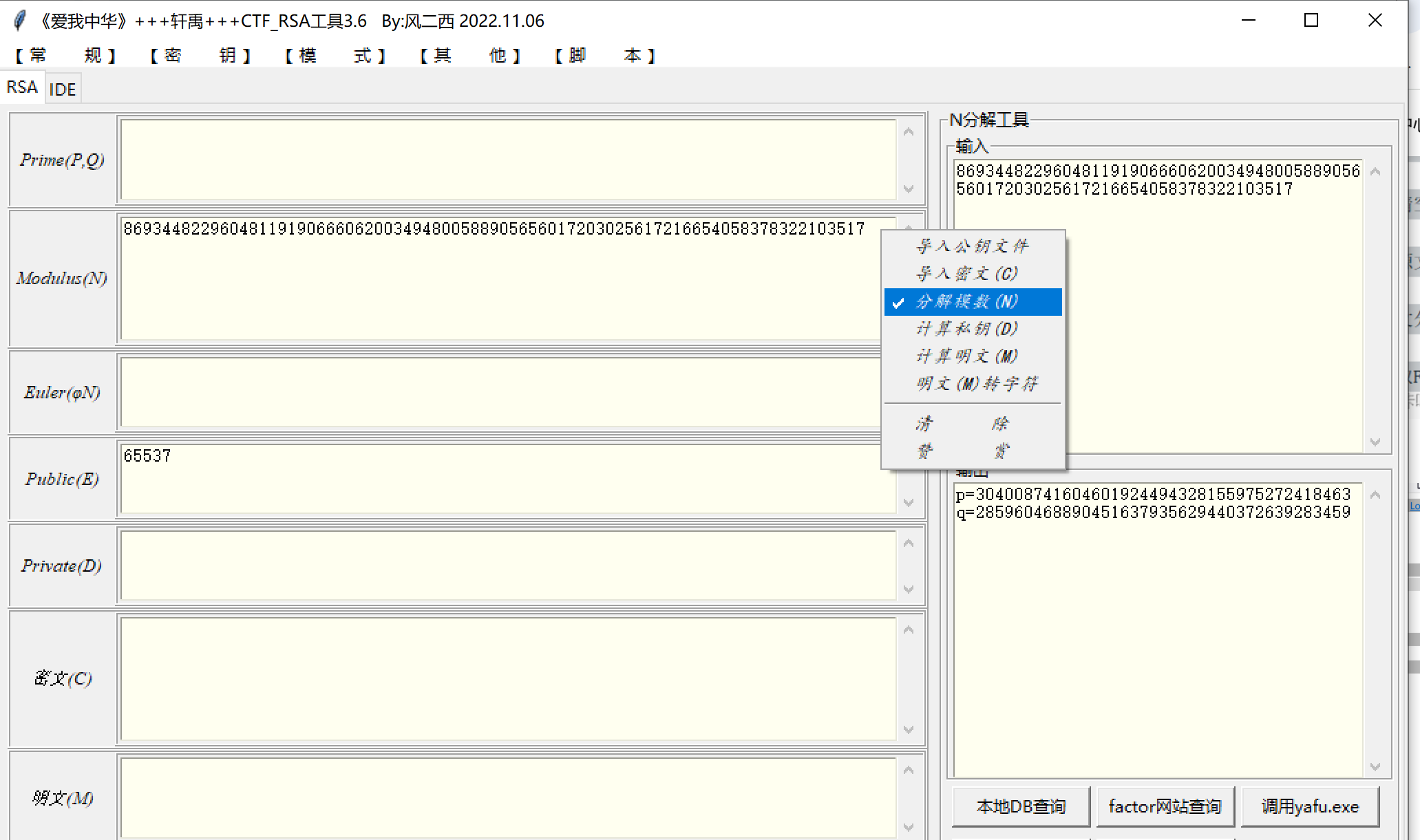
p=304008741604601924494328155975272418463
q=285960468890451637935629440372639283459
按照顺序,填入p,q,计算phiN,d
导入密文文件

计算明文得到十进制数字,左上角转换成字符

flag{decrypt_256}
RSAROLL
题目好难理解
给了两个文件,分别为题目:
RSA roll!roll!roll!
Only number and a-z
(don't use editor
which MS provide)
和
{920139713,19}704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148
没看懂啥意思
思路:已知比较小得n和e,用n分解模数得到p和q,用(p-1)(q-1)和e得到d
pow(c,d,n)即可得密文
即:n=920139713,e=19
使用轩禹分解N
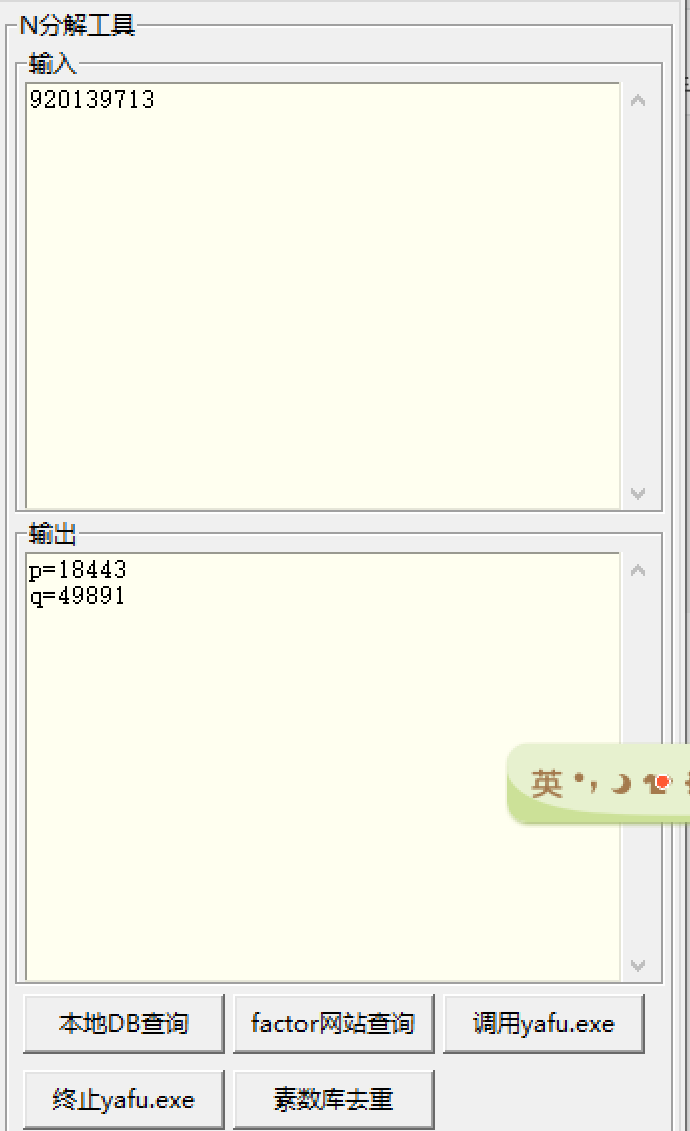 p=18443
p=18443
q=49891
填入轩禹

但是需要一个一个解,网上找了一个爆破脚本
# 已知n:920139713和e:19 大量密文c
# 用比较小的n分解模数得到p = 18443 q = 49891
# 由(p-1)(q-1)和e得到d
# pow(c,d,n)得明文import gmpy2
n = 920139713
p =gmpy2.mpz(18443)
q =gmpy2.mpz(49891)
e =gmpy2.mpz(19)
phi_n= (p - 1) * (q - 1)
d = gmpy2.invert(e, phi_n)
print("d is:%d"%(d))
#d is:96849619
c = [704796792,752211152,274704164,18414022,368270835,483295235,263072905,459788476,483295235,459788476,663551792,475206804,459788476,428313374,475206804,459788476,425392137,704796792,458265677,341524652,483295235,534149509,425392137,428313374,425392137,341524652,458265677,263072905,483295235,828509797,341524652,425392137,475206804,428313374,483295235,475206804,459788476,306220148]
m = []
for i in c:m.append(pow(i,d,n)) #用i遍历c
print(m)
for i in m:print(chr(i),end='')
#flag{13212je2ue28fy71w8u87y31r78eu1e2}
Dangerous RSA
N很大没办法分解,但是e非常小,使用轩禹模式中小e攻击直接梭哈

flag{25df8caf006ee5db94d48144c33b2c3b}
[GUET-CTF2019]BabyRSA
简单的数学转换
from Crypto.Util.number import *
from gmpy2 import *a = 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
b = 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
d = 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
e = 0xe6b1bee47bd63f615c7d0a43c529d219
enc_flag = 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a#b = p+q
#a = (p+1)*(q+1)
#phi = (p-1)*(q-1)=(p+1)*(q+1)-2b=a-2b
#phi = n-b+1
#n = phi+b-1=a-2b+b-1
n = a-b-1
m = powmod(enc_flag, d, n)
flag = long_to_bytes(m)
print(flag)
flag{cc7490e-78ab-11e9-b422-8ba97e5da1fd}
rsa2
通过轩禹分解可得p,q,d
需要考虑python2中hex转换完后面有L
md5不一样,需要手动添加
import hashlib
N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
d = 8920758995414587152829426558580025657357328745839747693739591820283538307445
# Convert 'd' to hex, then encode to bytes before hashing
#flag = "flag{" + hashlib.md5(hex(d).encode('utf-8')).hexdigest() + "}"
# hex(d).encode('utf-8') python3to2 b'0x13b8f87d588e2aa4a27296cf2898f56ab4c8deb5a1222ec080e23afecaf7f975L'
print("flag{" + hashlib.md5(b'0x13b8f87d588e2aa4a27296cf2898f56ab4c8deb5a1222ec080e23afecaf7f975L').hexdigest() + "}")# flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"
flag{47bf28da384590448e0b0d23909a25a4}
RSA5
给了一个e , 然后给了一大批c和 n,写个脚本看了一下这些 , 发现这些n里面存在不互质的数对。从而这题就是模不互质攻击。
研究了一下轩禹,发现脚本是空的。手动在网上找到了脚本添加进去
import gmpy2
import libnume = 65537
# 需要先求有最大公约数的几对nc
'''
n1 = 20474918894051778533305262345601880928088284471121823754049725354072477155873778848055073843345820697886641086842612486541250183965966001591342031562953561793332341641334302847996108417466360688139866505179689516589305636902137210185624650854906780037204412206309949199080005576922775773722438863762117750429327585792093447423980002401200613302943834212820909269713876683465817369158585822294675056978970612202885426436071950214538262921077409076160417436699836138801162621314845608796870206834704116707763169847387223307828908570944984416973019427529790029089766264949078038669523465243837675263858062854739083634207
c1 = 974463908243330865728978769213595400782053398596897741316275722596415018912929508637393850919224969271766388710025195039896961956062895570062146947736340342927974992616678893372744261954172873490878805483241196345881721164078651156067119957816422768524442025688079462656755605982104174001635345874022133045402344010045961111720151990412034477755851802769069309069018738541854130183692204758761427121279982002993939745343695671900015296790637464880337375511536424796890996526681200633086841036320395847725935744757993013352804650575068136129295591306569213300156333650910795946800820067494143364885842896291126137320
n20 = 26809700251171279102974962949184411136459372267620535198421449833298448092580497485301953796619185339316064387798092220298630428207556482805739803420279056191194360049651767412572609187680508073074653291350998253938793269214230457117194434853888765303403385824786231859450351212449404870776320297419712486574804794325602760347306432927281716160368830187944940128907971027838510079519466846176106565164730963988892400240063089397720414921398936399927948235195085202171264728816184532651138221862240969655185596628285814057082448321749567943946273776184657698104465062749244327092588237927996419620170254423837876806659
#……补充nc
c20 = 386213556608434013769864727123879412041991271528990528548507451210692618986652870424632219424601677524265011043146748309774067894985069288067952546139416819404039688454756044862784630882833496090822568580572859029800646671301748901528132153712913301179254879877441322285914544974519727307311002330350534857867516466612474769753577858660075830592891403551867246057397839688329172530177187042229028685862036140779065771061933528137423019407311473581832405899089709251747002788032002094495379614686544672969073249309703482556386024622814731015767810042969813752548617464974915714425595351940266077021672409858645427346n=[n1,n2,n3,n4,n5,n6,n7,n8,n9,n10,n11,n12,n13,n14,n15,n16,n17,n18,n19,n20]for i in range(len(n)):for j in range(i+1,len(n)):if(gmpy2.gcd(n[i],n[j])!=1):print(i,j)
'''
# 若存在最大公约数的一对nc,则模不互素,进行计算
n1 = 19591441383958529435598729113936346657001352578357909347657257239777540424811749817783061233235817916560689138344041497732749011519736303038986277394036718790971374656832741054547056417771501234494768509780369075443550907847298246275717420562375114406055733620258777905222169702036494045086017381084272496162770259955811174440490126514747876661317750649488774992348005044389081101686016446219264069971370646319546429782904810063020324704138495608761532563310699753322444871060383693044481932265801505819646998535192083036872551683405766123968487907648980900712118052346174533513978009131757167547595857552370586353973
c1 = 3834917098887202931981968704659119341624432294759361919553937551053499607440333234018189141970246302299385742548278589896033282894981200353270637127213483172182529890495903425649116755901631101665876301799865612717750360089085179142750664603454193642053016384714515855868368723508922271767190285521137785688075622832924829248362774476456232826885801046969384519549385428259591566716890844604696258783639390854153039329480726205147199247183621535172450825979047132495439603840806501254997167051142427157381799890725323765558803808030109468048682252028720241357478614704610089120810367192414352034177484688502364022887
n2 = 22822039733049388110936778173014765663663303811791283234361230649775805923902173438553927805407463106104699773994158375704033093471761387799852168337898526980521753614307899669015931387819927421875316304591521901592823814417756447695701045846773508629371397013053684553042185725059996791532391626429712416994990889693732805181947970071429309599614973772736556299404246424791660679253884940021728846906344198854779191951739719342908761330661910477119933428550774242910420952496929605686154799487839923424336353747442153571678064520763149793294360787821751703543288696726923909670396821551053048035619499706391118145067
c2 = 15406498580761780108625891878008526815145372096234083936681442225155097299264808624358826686906535594853622687379268969468433072388149786607395396424104318820879443743112358706546753935215756078345959375299650718555759698887852318017597503074317356745122514481807843745626429797861463012940172797612589031686718185390345389295851075279278516147076602270178540690147808314172798987497259330037810328523464851895621851859027823681655934104713689539848047163088666896473665500158179046196538210778897730209572708430067658411755959866033531700460551556380993982706171848970460224304996455600503982223448904878212849412357p = gmpy2.gcd(n1, n2)
q = n1 // p
m = gmpy2.powmod(c1, gmpy2.invert(e, (p-1)*(q-1)), n1)
print(libnum.n2s(int(m)))

flag{abdcbe5fd94e23b3de429223ab9c2fdf}
[NCTF2019]childRSA
给了一堆代码没看懂,把N直接扔轩禹离分解,点击本地DB或者factor

逐一计算p,q phin,d,m,转字符

NCTF{Th3r3_ar3_1ns3cure_RSA_m0duli_7hat_at_f1rst_gl4nce_appe4r_t0_be_s3cur3}
[HDCTF2019]bbbbbbrsa
from base64 import b64encode as b32encode
from gmpy2 import invert,gcd,iroot
from Crypto.Util.number import *
from binascii import a2b_hex,b2a_hex
import randomflag = "******************************"nbit = 128p = getPrime(nbit)
q = getPrime(nbit)
n = p*qprint p
print nphi = (p-1)*(q-1)e = random.randint(50000,70000)while True:if gcd(e,phi) == 1:break;else:e -= 1;c = pow(int(b2a_hex(flag),16),e,n)print b32encode(str(c))[::-1]# 2373740699529364991763589324200093466206785561836101840381622237225512234632
enc文件:
p = 177077389675257695042507998165006460849
n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
c = ==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM
逆序得到c之后base64解码
a = '==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM'
print(a[::-1])
#MjM3Mzc0MDY5OTUyOTM2NDk5MTc2MzU4OTMyNDIwMDA5MzQ2NjIwNjc4NTU2MTgzNjEwMTg0MDM4MTYyMjIzNzIyNTUxMjIzNDYzMg==
#2373740699529364991763589324200093466206785561836101840381622237225512234632
爆破e,匹配flag字符串
import gmpy2
import hashlib
import binascii
from Crypto.Util.number import *c = 2373740699529364991763589324200093466206785561836101840381622237225512234632
p = 177077389675257695042507998165006460849
n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
q = n//p
phi = (p-1)*(q-1)
for e in range(50000,70000):if(gmpy2.gcd(e,phi)==1):d = gmpy2.invert(e,phi)m = gmpy2.powmod(c,d,n)flag = str(long_to_bytes(m))if 'flag' in flag:print(flag)
b’flag{rs4_1s_s1mpl3!#}’
在轩禹文件路径下
\轩禹CTF_RSA工具3.6\rsascript\基础脚本
增加爆破e的脚本,重新打开轩禹,可以看到基础脚本里已经添加了!!
RSA4
给了三对NC,使用中国剩余扩展定理可以解出,轩禹有这个的脚本但是没办法解,有点奇怪。找了网上的脚本。
from Crypto.Util.number import long_to_bytes
import gmpy2N1 = int('331310324212000030020214312244232222400142410423413104441140203003243002104333214202031202212403400220031202142322434104143104244241214204444443323000244130122022422310201104411044030113302323014101331214303223312402430402404413033243132101010422240133122211400434023222214231402403403200012221023341333340042343122302113410210110221233241303024431330001303404020104442443120130000334110042432010203401440404010003442001223042211442001413004',5)
c1 = int('310020004234033304244200421414413320341301002123030311202340222410301423440312412440240244110200112141140201224032402232131204213012303204422003300004011434102141321223311243242010014140422411342304322201241112402132203101131221223004022003120002110230023341143201404311340311134230140231412201333333142402423134333211302102413111111424430032440123340034044314223400401224111323000242234420441240411021023100222003123214343030122032301042243',5)
N2 = int('302240000040421410144422133334143140011011044322223144412002220243001141141114123223331331304421113021231204322233120121444434210041232214144413244434424302311222143224402302432102242132244032010020113224011121043232143221203424243134044314022212024343100042342002432331144300214212414033414120004344211330224020301223033334324244031204240122301242232011303211220044222411134403012132420311110302442344021122101224411230002203344140143044114',5)
c2 = int('112200203404013430330214124004404423210041321043000303233141423344144222343401042200334033203124030011440014210112103234440312134032123400444344144233020130110134042102220302002413321102022414130443041144240310121020100310104334204234412411424420321211112232031121330310333414423433343322024400121200333330432223421433344122023012440013041401423202210124024431040013414313121123433424113113414422043330422002314144111134142044333404112240344',5)
N3 = int('332200324410041111434222123043121331442103233332422341041340412034230003314420311333101344231212130200312041044324431141033004333110021013020140020011222012300020041342040004002220210223122111314112124333211132230332124022423141214031303144444134403024420111423244424030030003340213032121303213343020401304243330001314023030121034113334404440421242240113103203013341231330004332040302440011324004130324034323430143102401440130242321424020323',5)
c3 = int('10013444120141130322433204124002242224332334011124210012440241402342100410331131441303242011002101323040403311120421304422222200324402244243322422444414043342130111111330022213203030324422101133032212042042243101434342203204121042113212104212423330331134311311114143200011240002111312122234340003403312040401043021433112031334324322123304112340014030132021432101130211241134422413442312013042141212003102211300321404043012124332013240431242',5)
e=3
M1=N2*N3
M2=N1*N3
M3=N1*N2
C=(c1*M1*gmpy2.invert(M1,N1)+c2*M2*gmpy2.invert(M2,N2)+c3*M3*gmpy2.invert(M3,N3))%(N1*N2*N3)
m=gmpy2.iroot(C,3)[0]
print(long_to_bytes(m))
flag{D4mn_y0u_h4s74d_wh47_4_b100dy_b4s74rd!}
[BJDCTF2020]rsa_output
仔细观察,题目中{}中的第一位相同,可以才到是共模攻击。
轩禹一把梭,按照e1,e2的格式填入,选择模式中的共模攻击,得到flag

BJD{r3a_C0mmoN_moD@_4ttack}
[BJDCTF2020]RSA
from Crypto.Util.number import getPrime,bytes_to_longflag=open("flag","rb").read()p=getPrime(1024)
q=getPrime(1024)
assert(e<100000)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
print c,n
print pow(294,e,n)# 共用了q,即q是n1,n2的公约数,可以求q = math.gcd(n1, n2),也可以通过轩禹进行N分解得q
p=getPrime(1024)
n=p*q
m=bytes_to_long("BJD"*32)
c=pow(m,e,n)
print c,n'''
output:
c_flag = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n_flag = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
C_294 = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018p_flag=99855353761764939308265951492116976798674681282941462516956577712943717850048051273358745095906207085170915794187749954588685850452162165059831749303473106541930948723000882713453679904525655327168665295207423257922666721077747911860159181041422993030618385436504858943615630219459262419715816361781062898911
q_flag=135283423427545651023916134156519717109709399113553907832988770259402226695880524199087896377303631866790192008529658716376684328032075836094156150811025163336681163420875451747389868549203081743561907379260240665153166927504059379076555558704275659133135906827306189040804323574468819553401905127999523676067
n_new =p_new*q_flag
e = 52361
c2 = 979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721
n_new = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
'''
所以轩禹对应填入
p_flag=99855353761764939308265951492116976798674681282941462516956577712943717850048051273358745095906207085170915794187749954588685850452162165059831749303473106541930948723000882713453679904525655327168665295207423257922666721077747911860159181041422993030618385436504858943615630219459262419715816361781062898911
q_flag=135283423427545651023916134156519717109709399113553907832988770259402226695880524199087896377303631866790192008529658716376684328032075836094156150811025163336681163420875451747389868549203081743561907379260240665153166927504059379076555558704275659133135906827306189040804323574468819553401905127999523676067
c_flag = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n_flag = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037

逐一求解得BJD{p_is_common_divisor}
[WUSTCTF2020]babyrsa
c = 28767758880940662779934612526152562406674613203406706867456395986985664083182
n = 73069886771625642807435783661014062604264768481735145873508846925735521695159
e = 65537
轩禹一把梭

分解n逐个求解即得wctf2020{just_@_piece_0f_cak3}
[ACTF新生赛2020]crypto-rsa0
伪加密修改后打开
from Cryptodome.Util.number import *
import randomFLAG=#hidden, please solve it
flag=int.from_bytes(FLAG,byteorder = 'big')p=getPrime(512)
q=getPrime(512)print(p)
print(q)
N=p*q
e=65537
enc = pow(flag,e,N)
print (enc)
output:
p=9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411
q=7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223
enc=50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350
flag{n0w_y0u_see_RSA}
直接轩禹完事了,这题在搞笑…为啥解出这么少
[ACTF新生赛2020]crypto-rsa3
原理其实是pq过于接近或者差距过大时,可以用yafu分解
直接轩禹分解N
逐步填入得结果flag{p_and_q_should_not_be_so_close_in_value}
[GWCTF 2019]BabyRSA
import hashlib
import sympy
from Crypto.Util.number import *
from sympy.abc import a, b, cflag = 'GWHT{******}'
secret = '******'assert(len(flag) == 38)half = len(flag) / 2flag1 = flag[:half]
flag2 = flag[half:]secret_num = getPrime(1024) * bytes_to_long(secret)p = sympy.nextprime(secret_num)
q = sympy.nextprime(p)N = p * qe = 0x10001F1 = bytes_to_long(flag1)
F2 = bytes_to_long(flag2)c1 = F1 + F2
c2 = pow(F1, 3) + pow(F2, 3)
assert(c2 < N)m1 = pow(c1, e, N)
m2 = pow(c2, e, N)output = open('secret', 'w')
output.write('N=' + str(N) + '\n')
output.write('m1=' + str(m1) + '\n')
output.write('m2=' + str(m2) + '\n')
output.close()
'''
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546轩禹破解可得
p=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699
q=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737c1=2732509502629189160482346120094198557857912754
c2=5514544075236012543362261483183657422998274674127032311399076783844902086865451355210243586349132992563718009577051164928513093068525554
解方程
import gmpy2
import Crypto.Util.number as cun
from sympy import *
from sympy.abc import a, b, c
aa = solve([a + b - c1, pow(a, 3) + pow(b, 3) - c2], [a, b])
output
[(1141553212031156130619789508463772513350070909, 1590956290598033029862556611630426044507841845), (1590956290598033029862556611630426044507841845, 1141553212031156130619789508463772513350070909)]
'''
F1 = 1141553212031156130619789508463772513350070909
F2 = 1590956290598033029862556611630426044507841845print(cun.long_to_bytes(F1))
print(cun.long_to_bytes(F2))
print(cun.long_to_bytes(F2) + cun.long_to_bytes(F1))
GWHT{f709e0e2cfe7e530ca8972959a1033b2}
这道题学到了利用sympy库中solve方法解方程组
用 sympy.solve() 函数来解单一方程的调用方式可以表示为 sympy.solve(表达式,符号) 。怎样解exp ( x ) − 3 = 0 这个方程。
import sympy
from sympy import *d = sympy.Symbol("d")
b = sympy.solve(sympy.exp(d)-3,d)
print(b)
我理解是将方程的一侧全部变化为0后将另一侧填入表达式选项,后面填求解变量,可以联立方程组,以solve([f1(a,b),f2(a,b)],[a,b])的形式
SameMod
提示的很明显了,共模攻击
{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,773}
{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,839}message1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
message2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535

结果为ascii码,转换后可得
flag{whenwethinkitispossible}
[BJDCTF2020]easyrsa
可以直接在factor在线网站破解
from Crypto.Util.number import getPrime,bytes_to_long
from sympy import Derivative
from fractions import Fraction
from secret import flagp=getPrime(1024)
q=getPrime(1024)
e=65537
n=p*q
z=Fraction(1,Derivative(arctan(p),p))-Fraction(1,Derivative(arth(q),q))
m=bytes_to_long(flag)
c=pow(m,e,n)
print(c,z,n)
'''
output:
c=7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
z=32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
n=15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441
'''

但是基于离线情况下,还是需要搞清楚代码的意思z=Fraction(1,Derivative(arctan(p),p))-Fraction(1,Derivative(arth(q),q))
尝试使用deepseek-32b解释



直接得出结论为z=p2+q2
可知
z=p2+q2
n=p*q
使用上面提到solve方法
from sympy import *
from sympy.abc import a, b, cc2=7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
c1=32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
aa = solve([a*a+b*b-c1, a*b-c2], [a, b])
emmm结果不对,求大神指点!
网上的解析,也就是说z=Fraction(1,Derivative(arctan(p),p))-Fraction(1,Derivative(arth(q),q))相当于直接给出了计算公式,变换可得f(p,q)-z=0,代入solve
from sympy import *z=32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
n=15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441p, q = symbols('p q')const1 = (1 / diff(atan(p), p) - 1 / diff(atanh(q), q)) - z
const2 = p * q - n
solutions = solve((const1, const2), (p, q))
print(solutions)
[AFCTF2018]你能看出这是什么加密么
p=0x928fb6aa9d813b6c3270131818a7c54edb18e3806942b88670106c1821e0326364194a8c49392849432b37632f0abe3f3c52e909b939c91c50e41a7b8cd00c67d6743b4fq=0xec301417ccdffa679a8dcc4027dd0d75baf9d441625ed8930472165717f4732884c33f25d4ee6a6c9ae6c44aedad039b0b72cf42cab7f80d32b74061e=0x10001c=0x70c9133e1647e95c3cb99bd998a9028b5bf492929725a9e8e6d2e277fa0f37205580b196e5f121a2e83bc80a8204c99f5036a07c8cf6f96c420369b4161d2654a7eccbdaf583204b645e137b3bd15c5ce865298416fd5831cba0d947113ed5be5426b708b89451934d11f9aed9085b48b729449e461ff0863552149b965e22b6
轩禹一把梭,依次填入后左上角选择16进制转10进制
flag{R54_|5_KaTeX parse error: Expected group after '_' at position 2: 0_̲imp13}
[NCTF2019]babyRSA
from Crypto.Util.number import *
from flag import flagdef nextPrime(n):n += 2 if n & 1 else 1while not isPrime(n):n += 2return np = getPrime(1024)
q = nextPrime(p)
n = p * q
e = 0x10001
d = inverse(e, (p-1) * (q-1))
c = pow(bytes_to_long(flag.encode()), e, n)# d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
# c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
需要具体分析代码。
由于pq非常接近,e*d =k*phi-1,可以爆破k,使用爆破的k计算phi,分解可得p和q之后,确认(p-1)*(q-1)=phi,则得到真正的pq。
其中需要确定k的范围。print(len(bin(e*d-1)))2066-2048=16,相差16位
import gmpy2
import sympy
import libnumd = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
e = int(0x10001)
# e∗d-1 = k∗ ( p − 1 ) ( q − 1 )
# print(len(bin(e*d-1)))2066-2048=16,相差16位
# 爆破k
p = 0
q = 0
for k in range(pow(2, 15), pow(2, 16)):if (e * d - 1) % k == 0:phi = (e * d - 1) // kp = sympy.prevprime(gmpy2.iroot(phi, 2)[0])q = sympy.nextprime(p)if ((p - 1) * (q - 1) == phi):print(p)print(q)breakn = p * q
m = pow(c, d, n)
flag = libnum.n2s(int(m))
print(flag)
# 143193611591752210918770476402384783351740028841763223236102885221839966637073188462808195974548579833368313904083095786906479416347681923731100260359652426441593107755892485944809419189348311956308456459523437459969713060653432909873986596042482699670451716296743727525586437248462432327423361080811225075839
# 143193611591752210918770476402384783351740028841763223236102885221839966637073188462808195974548579833368313904083095786906479416347681923731100260359652426441593107755892485944809419189348311956308456459523437459969713060653432909873986596042482699670451716296743727525586437248462432327423361080811225076497
# b'NCTF{70u2_nn47h_14_v3ry_gOO0000000d}'
可怜的RSAimport gmpy2
题目包含一个公钥,可以在轩禹的上方【密钥】-【导入公钥】导入public.key
以及右键导入密文-flag密文

在轩禹中可以直接分解N得到pq,导入公钥和密文以后

但是一通操作下来的明文不太对,尝试轩禹里导出私钥
然后私钥解密,OAEP提示密文长度不对,蹲一个大佬解答

import libnum
import base64
from Crypto.Util.number import bytes_to_long , long_to_bytes
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
# n = int("25B18BF5F389097D17237866BB51CFF8DE922453749EBC403B0995C97C0E386D46C161CADFF77C69860DAE4791C214CF8487AAAA9F26E920A977834906038AEFB5C30827DFCF3FC9E9769544F94E07CDFE0872039A3A6262116678B261FB2D6B9D32539E92A153B3675629BAB3942E7D35E30F7EEF5ABF1C50D797D0CC88E1BDCCFD1A12EA6F7EF75C3727DBDF2E780F3428AE8F7A4FB7A89F184A365032B153F8425E845750EB2B7ABC02DC15CE0207507AA950863BB8480A78028DD62979944D6C633FAFA103E4DB28CE87F5A0C6ED4A2F2664427F565C7781AB6191456D971C7FFA395272374CEC0155E5F91189DB742E4C28B03A0FA11CFFB03173D2A4CCE6AE53" , 16)
with open("flag.enc" , "r") as f:c = f.read()
# c = "GVd1d3viIXFfcHapEYuo5fAvIiUS83adrtMW/MgPwxVBSl46joFCQ1plcnlDGfL19K/3PvChV6n5QGohzfVyz2Z5GdTlaknxvHDUGf5HCukokyPwK/1EYU7NzrhGE7J5jPdi0Aj7xi/Odxy0hGMgpaBLd/nL3N8O6i9pc4Gg3O8soOlciBG/6/xdfN3SzSStMYIN8nfZZMSq3xDDvz4YB7TcTBh4ik4wYhuC77gmT+HWOv5gLTNQ3EkZs5N3EAopy11zHNYU80yv1jtFGcluNPyXYttU5qU33jcp0Wuznac+t+AZHeSQy5vk8DyWorSGMiS+J4KNqSVlDs12EqXEqqJ0uA=="
c = base64.b64decode(c)
# print(c)
n = 79832181757332818552764610761349592984614744432279135328398999801627880283610900361281249973175805069916210179560506497075132524902086881120372213626641879468491936860976686933630869673826972619938321951599146744807653301076026577949579618331502776303983485566046485431039541708467141408260220098592761245010678592347501894176269580510459729633673468068467144199744563731826362102608811033400887813754780282628099443490170016087838606998017490456601315802448567772411623826281747245660954245413781519794295336197555688543537992197142258053220453757666537840276416475602759374950715283890232230741542737319569819793988431443
e = 65537
p = 3133337
q = 25478326064937419292200172136399497719081842914528228316455906211693118321971399936004729134841162974144246271486439695786036588117424611881955950996219646807378822278285638261582099108339438949573034101215141156156408742843820048066830863814362379885720395082318462850002901605689761876319151147352730090957556940842144299887394678743607766937828094478336401159449035878306853716216548374273462386508307367713112073004011383418967894930554067582453248981022011922883374442736848045920676341361871231787163441467533076890081721882179369168787287724769642665399992556052144845878600126283968890273067575342061776244939
# phi_n = (p - 1) * (q - 1)
phi_n = 79832156279006753615345318561177456585117025350436220800170683345721668590492578389881313968446670228753236035314235010635436738865498763695760331670690883248845129482154408647992608091727864280499372378565045529666497144667283734129531551500638961941603599845651403112576691705565535718498343779441613892280587634790561052031969693115780986025906530240372665863343404282790483795755094816852513540292393774320731730378097012076455188030122559902533733349199586750399700942907304508812908324737440157923063549034114221010461102115420375873851284970378813070633751075610203322805869405290105946772652464251994477732209053168
# d = gmpy2.invert(e, phi_n)
d = 406853230956379689450620815713768871010712825839536410687962650677800895818003893712259622281477453292088146173840036827322518131453630576229976208523593618949818777897059256426591560532784635697190752924923710375949616954069804342573867253630978123632384795587951365482103468722384133084798614863870775897915929475258974188300927376911833763105616386167881813301748585233563049693794370642976326692672223638908164822104832415788577945314264232531947860576966629150456995512932232264881080618006698700677529111454508900582785420549466798020451488168615035256292977390692401388790460066327347700109341639992159475755036449key_info = RSA.construct((n , e , d , p , q))
key = RSA.importKey(key_info.exportKey())#存在不同
key = PKCS1_OAEP.new(key)
flag = key.decrypt(c)
print(flag)
flag{R54_|5_$0_B0rin9}
[RoarCTF2019]babyRSA
import sympy
import randomdef myGetPrime():A= getPrime(513)print(A)B=A-random.randint(1e3,1e5)print(B)return sympy.nextPrime((B!)%A)
p=myGetPrime()
#A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
#B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596q=myGetPrime()
#A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
#B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026r=myGetPrime()n=p*q*r
#n=85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
c=pow(flag,e,n)
#e=0x1001
#c=75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428
#so,what is the flag?
天真的我以为可以直接分解pqr,果然现实教我做人。
找了一下风二西对于这个软件的讲解视频,发现他有一个弹药库
https://gitee.com/fengerxi/rsa_f2x
轩禹的正确使用方式:在IDE-目录右键添加下载下来的文件,查找发现有这个题…直接运行

但是,记录一下,这种阶乘的是威尔逊定理
(p-1)!%p=-1%p
(p-2)!%p=1%p
RoarCTF{wm-CongrAtu1ation4-1t4-ju4t-A-bAby-R4A}
[RoarCTF2019]RSA
认真分析了一波代码,发现不会解,直接把N扔轩禹试一下,emmm出来了p和q,没有e,猜测e=65537,可得flag……这题是这么做的吗……或者爆破e也可以
A=(((y%x)**5)%(x%y))**2019+y**316+(y+1)/x
p=next_prime(z*x*y)
q=next_prime(z)
A = 2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724n = 117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127c = 41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128

from Cryptodome.Util.number import long_to_bytes
from gmpy2 import *
from gmpy2 import gmpy2
from sympy import nextprime
from Cryptodome.Util.number import *
n = 117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
c = 41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128
e=65537
p=842868045681390934539739959201847552284980179958879667933078453950968566151662147267006293571765463137270594151138695778986165111380428806545593588078365331313084230014618714412959584843421586674162688321942889369912392031882620994944241987153078156389470370195514285850736541078623854327959382156753458569
q=139916095583110895133596833227506693679306709873174024876891023355860781981175916446323044732913066880786918629089023499311703408489151181886568535621008644997971982182426706592551291084007983387911006261442519635405457077292515085160744169867410973960652081452455371451222265819051559818441257438021073941183
phi=(p-1)*(q-1)## 爆破e
for e in range(1, 70000):try:d = gmpy2.invert(e, phi)flag = gmpy2.powmod(c, d, n)if b'CTF' in long_to_bytes(flag):print(long_to_bytes(flag))except:continue
RoarCTF{wm-l1l1ll1l1l1l111ll}
[网鼎杯 2020 青龙组]you_raise_me_up
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
import randomn = 2 ** 512
m = random.randint(2, n-1) | 1
c = pow(m, bytes_to_long(flag), n)
print 'm = ' + str(m)
print 'c = ' + str(c)# m = 391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
# c = 6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499
离谱,直接N分解不出来,惊觉N不是素数……啊这。
学到了,是离散对数…
使用轩禹的脚本离散对数梭哈

RSA & what
from Crypto.Util.number import bytes_to_long, getPrime
from random import randint
from gmpy2 import powmodp = getPrime(2048)
q = getPrime(2048)
N = p*q
Phi = (p-1)*(q-1)
def get_enc_key(N,Phi):e = getPrime(N)if Phi % e == 0:return get_enc_key(N, Phi)else:return e
e1 = get_enc_key(randint(10, 12), Phi)
e2 = get_enc_key(randint(10, 12), Phi)fr = open(r"./base64", "rb")#flag is in this file
f1 = open(r"./HUB1", "wb")
f2 = open(r"./HUB2", "wb")
base64 = fr.read(255)
f1.write("%d\n%d\n" % (N, e1))
f2.write("%d\n%d\n" % (N, e2))
while len(base64)>0:pt = bytes_to_long(base64)ct1 = powmod(pt, e1, N)ct2 = powmod(pt, e2, N)f1.write("\n%d" % ct1)f2.write("\n%d" % ct2)base64 = fr.read(255)
fr.close()
f1.close()
f2.close()
以下参考了网上大佬的wp,做到这儿实在是解不动了,本菜先去做做web开心一下…
首先,我们审计题目,发现题目中给给予了我们许多c1组和c2组,其中N值和两组分别对应的e值我们都知晓,所有我们可知这是一个共模攻击问题:
一、扩展欧几里得算法求解出e1、e2值对应的s1和s2:
from Crypto.Util.number import *
import gmpy2
def egcd(a,b):if b==0:return a,0else:x,y=egcd(b,a%b)return y,x-(a//b)*y
S=egcd(e1,e2)
s1=S[0]
s2=S[1]
当然,gmpy2.gcdext(e1,e2)也可以;
二、求解出m值(共模攻击)
M=b''
for i in range(0,6):m=(gmpy2.powmod(c1[i],s1,N)*gmpy2.powmod(c2[i],s2,N))%NM+=long_to_bytes(m)
print(M)
output:
b'VEhJUz==\nRkxBR3==\nSVN=\nSElEREVOLo==\nQ0FO\nWU9V\nRklORM==\nSVT=\nT1VUP4==\nRE8=\nWU9V\nS05PV9==\nQkFTRTY0P5==\nWW91bmdD\nVEhJTku=\nWU9V\nQVJF\nTk9U\nVEhBVE==\nRkFNSUxJQVI=\nV0lUSO==\nQkFTRTY0Lh==\nQmFzZTY0\naXO=\nYW==\nZ3JvdXA=\nb2b=\nc2ltaWxhcn==\nYmluYXJ5LXRvLXRleHR=\nZW5jb2Rpbme=\nc2NoZW1lc0==\ndGhhdD==\ncmVwcmVzZW50\nYmluYXJ5\nZGF0YW==\naW5=\nYW6=\nQVNDSUl=\nc3RyaW5n\nZm9ybWF0\nYnk=\ndHJhbnNsYXRpbmd=\naXS=\naW50b1==\nYT==\ncmFkaXgtNjQ=\ncmVwcmVzZW50YXRpb24u\nVGhl\ndGVybc==\nQmFzZTY0\nb3JpZ2luYXRlc8==\nZnJvbd==\nYY==\nc3BlY2lmaWN=\nTUlNRT==\nY29udGVudI==\ndHJhbnNmZXI=\nZW5jb2Rpbmcu\nVGhl\ncGFydGljdWxhct==\nc2V0\nb2b=\nNjR=\nY2hhcmFjdGVyc5==\nY2hvc2Vu\ndG+=\ncmVwcmVzZW50\ndGhl\nNjQ=\ncGxhY2UtdmFsdWVz\nZm9y\ndGhl\nYmFzZd==\ndmFyaWVz\nYmV0d2Vlbt==\naW1wbGVtZW50YXRpb25zLp==\nVGhl\nZ2VuZXJhbI==\nc3RyYXRlZ3n=\naXO=\ndG9=\nY2hvb3Nl\nNjR=\nY2hhcmFjdGVyc5==\ndGhhdA==\nYXJl\nYm90aN==\nbWVtYmVyc5==\nb2a=\nYS==\nc3Vic2V0\nY29tbW9u\ndG8=\nbW9zdM==\nZW5jb2RpbmdzLA==\nYW5k\nYWxzb8==\ncHJpbnRhYmxlLg==\nVGhpc9==\nY29tYmluYXRpb25=\nbGVhdmVz\ndGhl\nZGF0YW==\ndW5saWtlbHk=\ndG/=\nYmV=\nbW9kaWZpZWS=\naW5=\ndHJhbnNpdE==\ndGhyb3VnaN==\naW5mb3JtYXRpb26=\nc3lzdGVtcyw=\nc3VjaN==\nYXM=\nRS1tYWlsLD==\ndGhhdA==\nd2VyZQ==\ndHJhZGl0aW9uYWxseQ==\nbm90\nOC1iaXQ=\nY2xlYW4uWzFd\nRm9y\nZXhhbXBsZSw=\nTUlNRSdz\nQmFzZTY0\naW1wbGVtZW50YXRpb24=\ndXNlcw==\nQahDWiw=\nYahDeiw=\nYW5k\nMKhDOQ==\nZm9y\ndGhl\nZmlyc3Q=\nNjI=\ndmFsdWVzLg==\nT3RoZXI=\ndmFyaWF0aW9ucw==\nc2hhcmU=\ndGhpcw==\ncHJvcGVydHk=\nYnV0\nZGlmZmVy\naW4=\ndGhl\nc3ltYm9scw==\nY2hvc2Vu\nZm9y\ndGhl\nbGFzdA==\ndHdv\ndmFsdWVzOw==\nYW4=\nZXhhbXBsZQ==\naXM=\nVVRGLTcu'
我们对他进行以下整理,删除他的\符号:
VEhJUz==
RkxBR3==
SVN=
SElEREVOLo==
Q0FO
WU9V
RklORM==
SVT=
T1VUP4==
RE8=
WU9V
S05PV9==
QkFTRTY0P5==
WW91bmdD
VEhJTku=
WU9V
QVJF
Tk9U
VEhBVE==
RkFNSUxJQVI=
V0lUSO==
QkFTRTY0Lh==
QmFzZTY0
aXO=
YW==
Z3JvdXA=
b2b=
c2ltaWxhcn==
YmluYXJ5LXRvLXRleHR=
ZW5jb2Rpbme=
c2NoZW1lc0==
dGhhdD==
cmVwcmVzZW50
YmluYXJ5
ZGF0YW==
aW5=
YW6=
QVNDSUl=
c3RyaW5n
Zm9ybWF0
Ynk=
dHJhbnNsYXRpbmd=
aXS=
aW50b1==
YT==
cmFkaXgtNjQ=
cmVwcmVzZW50YXRpb24u
VGhl
dGVybc==
QmFzZTY0
b3JpZ2luYXRlc8==
ZnJvbd==
YY==
c3BlY2lmaWN=
TUlNRT==
Y29udGVudI==
dHJhbnNmZXI=
ZW5jb2Rpbmcu
VGhl
cGFydGljdWxhct==
c2V0
b2b=
NjR=
Y2hhcmFjdGVyc5==
Y2hvc2Vu
dG+=
cmVwcmVzZW50
dGhl
NjQ=
cGxhY2UtdmFsdWVz
Zm9y
dGhl
YmFzZd==
dmFyaWVz
YmV0d2Vlbt==
aW1wbGVtZW50YXRpb25zLp==
VGhl
Z2VuZXJhbI==
c3RyYXRlZ3n=
aXO=
dG9=
Y2hvb3Nl
NjR=
Y2hhcmFjdGVyc5==
dGhhdA==
YXJl
Ym90aN==
bWVtYmVyc5==
b2a=
YS==
c3Vic2V0
Y29tbW9u
dG8=
bW9zdM==
ZW5jb2RpbmdzLA==
YW5k
YWxzb8==
cHJpbnRhYmxlLg==
VGhpc9==
Y29tYmluYXRpb25=
bGVhdmVz
dGhl
ZGF0YW==
dW5saWtlbHk=
dG/=
YmV=
bW9kaWZpZWS=
aW5=
dHJhbnNpdE==
dGhyb3VnaN==
aW5mb3JtYXRpb26=
c3lzdGVtcyw=
c3VjaN==
YXM=
RS1tYWlsLD==
dGhhdA==
d2VyZQ==
dHJhZGl0aW9uYWxseQ==
bm90
OC1iaXQ=
Y2xlYW4uWzFd
Rm9y
ZXhhbXBsZSw=
TUlNRSdz
QmFzZTY0
aW1wbGVtZW50YXRpb24=
dXNlcw==
QahDWiw=
YahDeiw=
YW5k
MKhDOQ==
Zm9y
dGhl
Zmlyc3Q=
NjI=
dmFsdWVzLg==
T3RoZXI=
dmFyaWF0aW9ucw==
c2hhcmU=
dGhpcw==
cHJvcGVydHk=
YnV0
ZGlmZmVy
aW4=
dGhl
c3ltYm9scw==
Y2hvc2Vu
Zm9y
dGhl
bGFzdA==
dHdv
dmFsdWVzOw==
YW4=
ZXhhbXBsZQ==
aXM=
VVRGLTcu
发现这是一个base64码,对其进行base64解码,发现得到的不是我们所需的flag,借鉴大佬,可能为base64隐写(不太了解),于是借鉴了大佬的代码:
# py2
def get_base64_diff_value(s1, s2):base64chars = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'res = 0for i in xrange(len(s2)):if s1[i] != s2[i]:return abs(base64chars.index(s1[i]) - base64chars.index(s2[i]))return res
def solve_stego():with open('2.txt', 'rb') as f:file_lines = f.readlines()bin_str = ''for line in file_lines:steg_line = line.replace('\n', '')norm_line = line.replace('\n', '').decode('base64').encode('base64').replace('\n', '')diff = get_base64_diff_value(steg_line, norm_line)pads_num = steg_line.count('=')if diff:bin_str += bin(diff)[2:].zfill(pads_num * 2)else:bin_str += '0' * pads_num * 2res_str = ''for i in xrange(0, len(bin_str), 8):res_str += chr(int(bin_str[i:i+8], 2))print res_str
solve_stego()
flag{7c86d8f7d6de33a87f7f9d6b005ce640}
[NPUCTF2020]EzRSA
from gmpy2 import lcm , powmod , invert , gcd , mpz
from Crypto.Util.number import getPrime
from sympy import nextprime
from random import randint
p = getPrime(1024)
q = getPrime(1024)
n = p * q
gift = lcm(p - 1 , q - 1)
e = 54722
flag = b'NPUCTF{******************}'
m = int.from_bytes(flag , 'big')
c = powmod(m , e , n)
print('n: ' , n)
print('gift: ' , gift)
print('c: ' , c)#n: 17083941230213489700426636484487738282426471494607098847295335339638177583685457921198569105417734668692072727759139358207667248703952436680183153327606147421932365889983347282046439156176685765143620637107347870401946946501620531665573668068349080410807996582297505889946205052879002028936125315312256470583622913646319779125559691270916064588684997382451412747432722966919513413709987353038375477178385125453567111965259721484997156799355617642131569095810304077131053588483057244340742751804935494087687363416921314041547093118565767609667033859583125275322077617576783247853718516166743858265291135353895239981121
#gift: 2135492653776686212553329560560967285303308936825887355911916917454772197960682240149821138177216833586509090969892419775958406087994054585022894165950768427741545736247918410255804894522085720642952579638418483800243368312702566458196708508543635051350999572787188236243275631609875253617015664414032058822919469443284453403064076232765024248435543326597418851751586308514540124571309152787559712950209357825576896132278045112177910266019741013995106579484868768251084453338417115483515132869594712162052362083414163954681306259137057581036657441897428432575924018950961141822554251369262248368899977337886190114104
#c: 3738960639194737957667684143565005503596276451617922474669745529299929395507971435311181578387223323429323286927370576955078618335757508161263585164126047545413028829873269342924092339298957635079736446851837414357757312525158356579607212496060244403765822636515347192211817658170822313646743520831977673861869637519843133863288550058359429455052676323196728280408508614527953057214779165450356577820378810467527006377296194102671360302059901897977339728292345132827184227155061326328585640019916328847372295754472832318258636054663091475801235050657401857262960415898483713074139212596685365780269667500271108538319
已经给了n,c,正常逻辑是使用轩禹分解,但是考虑在没有网的情况下,可以爆破。
gift = lcm(p - 1 , q - 1)#两个大素数的最小公倍数就是他俩的乘积,可以通过solve解出p和q
import sympy
from sympy import *
from gmpy2 import lcmp = sympy.Symbol("p")
q = sympy.Symbol("q")
n=17083941230213489700426636484487738282426471494607098847295335339638177583685457921198569105417734668692072727759139358207667248703952436680183153327606147421932365889983347282046439156176685765143620637107347870401946946501620531665573668068349080410807996582297505889946205052879002028936125315312256470583622913646319779125559691270916064588684997382451412747432722966919513413709987353038375477178385125453567111965259721484997156799355617642131569095810304077131053588483057244340742751804935494087687363416921314041547093118565767609667033859583125275322077617576783247853718516166743858265291135353895239981121
gift=2135492653776686212553329560560967285303308936825887355911916917454772197960682240149821138177216833586509090969892419775958406087994054585022894165950768427741545736247918410255804894522085720642952579638418483800243368312702566458196708508543635051350999572787188236243275631609875253617015664414032058822919469443284453403064076232765024248435543326597418851751586308514540124571309152787559712950209357825576896132278045112177910266019741013995106579484868768251084453338417115483515132869594712162052362083414163954681306259137057581036657441897428432575924018950961141822554251369262248368899977337886190114104aaa = sympy.solve([(p - 1) * (q - 1)-gift,p*q-n],[p,q])
print(aaa)
结果是没有解出来,求问为什么…
在线状态下可以直接在factor求出来pq
需要注意的出现了!
gcd(e,phi)=2,存在公约数2
所以正常求解时解不出来M
e整除2e // 2,从而让其与phi互质,这样就可以求d了。
注意,我们求出d之后,如果直接:m=pow(c,int(d),n)
求出来的不是m,而是m的平方。
为什么呢:
c=(m^e) mod n 经过变型 => c=((m2)e/2)mod n
因为我们用的是e//2,所以其实得到的是m^2
也就是说求出来m之后记得开个平方。
from gmpy2 import gmpy2
from sympy import *
from Crypto.Util.number import *
from gmpy2 import *
n = 17083941230213489700426636484487738282426471494607098847295335339638177583685457921198569105417734668692072727759139358207667248703952436680183153327606147421932365889983347282046439156176685765143620637107347870401946946501620531665573668068349080410807996582297505889946205052879002028936125315312256470583622913646319779125559691270916064588684997382451412747432722966919513413709987353038375477178385125453567111965259721484997156799355617642131569095810304077131053588483057244340742751804935494087687363416921314041547093118565767609667033859583125275322077617576783247853718516166743858265291135353895239981121
gift = 2135492653776686212553329560560967285303308936825887355911916917454772197960682240149821138177216833586509090969892419775958406087994054585022894165950768427741545736247918410255804894522085720642952579638418483800243368312702566458196708508543635051350999572787188236243275631609875253617015664414032058822919469443284453403064076232765024248435543326597418851751586308514540124571309152787559712950209357825576896132278045112177910266019741013995106579484868768251084453338417115483515132869594712162052362083414163954681306259137057581036657441897428432575924018950961141822554251369262248368899977337886190114104
c = 3738960639194737957667684143565005503596276451617922474669745529299929395507971435311181578387223323429323286927370576955078618335757508161263585164126047545413028829873269342924092339298957635079736446851837414357757312525158356579607212496060244403765822636515347192211817658170822313646743520831977673861869637519843133863288550058359429455052676323196728280408508614527953057214779165450356577820378810467527006377296194102671360302059901897977339728292345132827184227155061326328585640019916328847372295754472832318258636054663091475801235050657401857262960415898483713074139212596685365780269667500271108538319
phi =(p-1)*(q-1)
e1 = e//2
d = gmpy2.invert(e1,phi) #私钥d则是使用gmpy2库求解逆元得出。
m2=gmpy2.powmod(c,d,n)
m=gmpy2.iroot(m2,2)[0] #开平方
print(binascii.unhexlify(hex(m)[2:]))
# NPUCTF{diff1cult_rsa_1s_e@sy}
其实没有理解为什么最后结果要开方。但是这道题一让我知道要确认e,phi不互素。
使用轩禹-IDA-【脚本】-e和phi不互素,可以直接梭哈
因为这个题gift相当于直接给出了phi,e,n,c,就可以解

[MRCTF2020]babyRSA
这段代码实现了一个自定义的RSA加密过程,并提供了部分参数让我们能够破解它获取flag。
-
生成素数p的过程(gen_p):
- 首先生成一个17个素数的数组P,每个素数都是前一个素数的下一个素数
- 打印出P[9]的值(第10个素数)
- 计算n = P[0]×P[1]×…×P[16]
- 生成一个1024位的随机素数p
- 计算factor = p^65537 mod n
- 返回p的下一个素数作为_P
-
生成素数q的过程(gen_q):
- 生成三个1024位素数sub_Q, Q_1, Q_2
- 计算 Q = sub_Q^Q_2 mod Q_1
- 返回Q的下一个素数作为_Q
-
加密过程:
- 使用标准的RSA加密,公钥指数e=65537
- 模数N = _P × _Q
- 加密flag得到密文_C
破解思路
-
恢复p:
- 已知P[9]可以恢复整个P数组(因为每个都是前一个的下一个素数)
- 已知factor = p^e mod n,可以解出p
- 然后_P就是p的下一个素数
-
恢复q:
- 直接给出了Q_1, Q_2, sub_Q,可以计算Q = sub_Q^Q_2 mod Q_1
- 然后_Q就是Q的下一个素数
-
解密RSA:
- 有了_P和_Q,可以计算φ(N)和私钥d
- 然后用标准RSA解密得到flag
import sympy
from gmpy2 import gcd, invert
from Crypto.Util.number import long_to_bytes# 给定数据
P_p = 206027926847308612719677572554991143421
P_factor = 213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
Q_1 = 103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2 = 151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q = 168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
Ciphertext = 1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832
e = 65537# 第一步:恢复P数组
def recover_P(P9):P = [0]*17P[9] = P9# 恢复前9个for i in range(8, -1, -1):P[i] = sympy.prevprime(P[i+1])# 恢复后7个for i in range(10, 17):P[i] = sympy.nextprime(P[i-1])return PP = recover_P(P_p)
n = 1
for pi in P:n *= pi# 第二步:解出p
# factor = p^e mod n => p^e ≡ factor mod n
# 由于n是多个小素数的乘积,可以在每个素数因子下求解
# 使用中国剩余定理
def nth_root_mod(c, e, factors):# 对每个因子求解 x^e ≡ c mod presidues = []moduli = []for p in factors:# 忽略不整除c的因子(但这里c=p^e mod n,应该都能整除)if gcd(c, p) != 1:# p整除c,所以x ≡ 0 mod presidues.append(0)moduli.append(p)continue# 计算phi(p) = p-1phi = p-1d = invert(e, phi)x = pow(c, d, p)residues.append(x)moduli.append(p)# 使用中国剩余定理合并from functools import reducedef crt(a, m):M = reduce(lambda x,y:x*y, m)result = 0for ai, mi in zip(a, m):Mi = M // miinv = invert(Mi, mi)result = (result + ai * Mi * inv) % Mreturn resultreturn crt(residues, moduli)p = nth_root_mod(P_factor, e, P)
# 检查是否正确
assert pow(p, e, n) == P_factor
# _P是p的下一个素数
_P = sympy.nextprime(p)# 第三步:恢复_Q
Q = pow(sub_Q, Q_2, Q_1)
_Q = sympy.nextprime(Q)# 第四步:RSA解密
N = _P * _Q
phi = (_P-1)*(_Q-1)
d = invert(e, phi)
M = pow(Ciphertext, d, N)
print(long_to_bytes(M))
#b'MRCTF{sti11_@_b@by_qu3st10n}'
运行这段代码应该能够解密出flag。代码的主要步骤是:
- 从已知的P[9]恢复整个P数组
- 使用中国剩余定理和离散对数解出p
- 计算_P为p的下一个素数
- 直接计算Q和_Q
- 最后进行标准RSA解密
注意:在实际运行中,可能需要安装必要的库(如gmpy2、sympy、pycryptodome等)。
其中,对于中间利用中国剩余定理的部分
中国剩余定理(CRT)在破解中的应用详解
在破解这个RSA问题的过程中,中国剩余定理(Chinese Remainder Theorem, CRT)是关键步骤之一。让我们详细解释这部分。
问题回顾
我们需要从已知的 P_factor = p^e mod n 中恢复出 p,其中:
e = 65537n = P[0] × P[1] × ... × P[16](17个连续素数的乘积)P_factor = p^65537 mod n
这相当于要解方程:x^65537 ≡ P_factor mod n
为什么需要CRT
因为 n 是多个小素数的乘积,我们可以利用CRT将这个大问题分解为多个小问题:
- 分别在每个小素数
P[i]的模数下求解x^65537 ≡ P_factor mod P[i] - 然后用CRT将这些解组合起来,得到模
n下的解
具体步骤详解
第一步:分解问题
对于每个素数因子 P[i],我们求解:
x ≡ r_i mod P[i],其中 r_i 满足 r_i^65537 ≡ P_factor mod P[i]
** 第二步:求解单个模数下的方程**
对于每个 P[i],我们需要解 x^e ≡ c mod P[i]:
- 如果
P[i]整除c(即c ≡ 0 mod P[i]),那么显然x ≡ 0 mod P[i] - 否则,我们可以计算:
φ(P[i]) = P[i] - 1(因为P[i]是素数)- 计算
d_i ≡ e^-1 mod φ(P[i])(求模逆) - 然后
x ≡ c^d_i mod P[i]
第三步:使用CRT组合解
现在我们有一组同余方程:
x ≡ r_0 mod P[0]
x ≡ r_1 mod P[1]
...
x ≡ r_16 mod P[16]
CRT告诉我们,如果模数两两互质(这里确实如此,因为P[i]都是不同素数),那么这个方程组有唯一解模 n = P[0]×P[1]×...×P[16]。
CRT的实现
具体计算步骤:
- 计算
N = P[0]×P[1]×...×P[16] - 对每个i,计算:
N_i = N / P[i]inv_i = N_i^-1 mod P[i](模逆)
- 解为
x ≡ sum(r_i × N_i × inv_i) mod N
为什么这样能得到正确的p
因为:
- 根据定义,
p^e ≡ P_factor mod n - 我们的解法找到了满足
x^e ≡ P_factor mod n的x - 由于
p < n(因为p是1024位素数,而n是17个128位素数的乘积,约2176位) - 所以
p就是我们找到的解
代码对应部分解释
def nth_root_mod(c, e, factors):residues = []moduli = []for p in factors:if gcd(c, p) != 1: # p divides cresidues.append(0)moduli.append(p)continuephi = p-1d = invert(e, phi) # 计算e的模逆x = pow(c, d, p) # 计算c^d mod presidues.append(x)moduli.append(p)# 使用中国剩余定理合并from functools import reducedef crt(a, m):M = reduce(lambda x,y:x*y, m)result = 0for ai, mi in zip(a, m):Mi = M // miinv = invert(Mi, mi)result = (result + ai * Mi * inv) % Mreturn resultreturn crt(residues, moduli)p = nth_root_mod(P_factor, e, P)
这段代码正是实现了上述过程:
- 对每个因子P[i],求解
x^e ≡ c mod P[i] - 使用CRT组合所有解
- 返回模n下的唯一解
总结
通过中国剩余定理,我们将一个在大模数 n 下的高次方根问题,分解为多个在小素数模数下的更易解决的问题,然后组合这些解得到最终答案。这是密码学中常见的技巧,特别适用于模数是多个小素数乘积的情况。
[WUSTCTF2020]情书
比较基础,但是需要注意的时候加了字母表转换
Premise: Enumerate the alphabet by 0銆�1銆�2銆�..... 銆�25
Using the RSA system
Encryption:0156 0821 1616 0041 0140 2130 1616 0793
Public Key:2537 and 13
Private Key:2537 and 937flag: wctf2020{Decryption}
exp:
import gmpy2
from Crypto.Cipher import PKCS1_OAEP
from Crypto.PublicKey import RSA
from Crypto.Util.number import long_to_bytes
n = 2537
e = 13
d = 937
c = '0156 0821 1616 0041 0140 2130 1616 0793'.split(' ')p = 43
q = 59
phi = (q-1) * (p-1)
m=[]
for x in c:m.append(chr(int(gmpy2.powmod(int(x),d,n))+ord('a')))
print(''.join(m))
# output:iloveyou
0156 0821 1616 0041 0140 2130 1616 0793,以空格分割,需要一个一个转,轩禹不支持四位一转- 使用
+ ord('a'),这是一种将 0-25 映射到 a-z 的常见方法
[WUSTCTF2020]dp_leaking_1s_very_d@angerous
第一次见把flag写在题目上的
e = 65537
n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825
泄露了dp,直接轩禹梭哈,在脚本里选择dp泄露,运行可得flag

flag{dp_leaking_1s_very_d@angerous}
[HDCTF2019]together
很奇怪,超明显的共模攻击,为什么轩禹没有梭哈出来,一堆乱码…
留一下能正常转出来的脚本
n1=14853081277902411240991719582265437298941606850989432655928075747449227799832389574251190347654658701773951599098366248661597113015221566041305501996451638624389417055956926238595947885740084994809382932733556986107653499144588614105694518150594105711438983069306254763078820574239989253573144558449346681620784979079971559976102366527270867527423001083169127402157598183442923364480383742653117285643026319914244072975557200353546060352744263637867557162046429886176035616570590229646013789737629785488326501654202429466891022723268768841320111152381619260637023031430545168618446134188815113100443559425057634959299
e1=0x091d
#print(e1)
n2=14853081277902411240991719582265437298941606850989432655928075747449227799832389574251190347654658701773951599098366248661597113015221566041305501996451638624389417055956926238595947885740084994809382932733556986107653499144588614105694518150594105711438983069306254763078820574239989253573144558449346681620784979079971559976102366527270867527423001083169127402157598183442923364480383742653117285643026319914244072975557200353546060352744263637867557162046429886176035616570590229646013789737629785488326501654202429466891022723268768841320111152381619260637023031430545168618446134188815113100443559425057634959299
e2=0x5b25
#print(e2)
f1='R3Noy6r3WLItytAmb4FmHEygoilucEEZbO9ZYXx5JN03HNpBLDx7fXd2fl+UL5+11RCs/y0qlTGURWWDtG66eNLzGwNpAKiVj6I7RtUJl2Pcm3NvFeAFwI9UsVREyh7zIV6sI9ZP8l/2GVDorLAz5ULW+f0OINGhJmZm8FL/aDnlfTElhQ87LPicWpXYoMtyr6WrxjK6Ontn8BqCt0EjQ7TeXZhxIH9VTPWjDmFdmOqaqdVIT+LZemTgLNESwM5nn4g5S3aFDFwj1YiDYl0/+8etvKfOrfoKOwR0CxsRHagwdUUTES8EcHLmMGCxCkDZn3SzmmA6Nb3lgLeSgG8P1A=='
f2='O+rRCXI3aTB6P1rYIOPUdalUp6ujpwEq4I20CoWA+HIL8xxGtqY6N5gpr0guZv9ZgOEAMFnBxOqMdVNnB9GgnhmXtt1ZWydPqIcHvlfwpd/Lyd0XSjXnjaz3P3vOQvR71cD/uXyBA0XPzmnTIMgEhuGJVFm8min0L/2qI7wg/Z7w1+4mOmi655JIXeCiG23ukDv6l9bZuqfGvWCa1KKXWDP31nLbp0ZN2obUs6jEAa1qVTaX6M4My+sks+0VvHATrAUuCrmMwVEivqIJ/nS6ymGVERN6Ohnzyr168knEBKOVj0FAOx3YLfppMM+XbOGHeqdKJRLpMvqFXDMGQInT3w=='
import base64
from Crypto.Util.number import *
c1=bytes_to_long(base64.b64decode(f1))
c2=bytes_to_long(base64.b64decode(f2))import gmpy2
S=gmpy2.gcdext(e1,e2)
s1=S[1]
s2=S[2]
print(s1)
print(s2)
m=(gmpy2.powmod(c1,s1,n1)*gmpy2.powmod(c2,s2,n1))%n1
print(long_to_bytes(m))
b’flag{23re_SDxF_y78hu_5rFgS}’
相关文章:

buuctf RSA之旅
BUUCTF-RSA的成长之路 rsarsaRSA1RSA3RSA2RSARSAROLLDangerous RSA[GUET-CTF2019]BabyRSArsa2RSA5[NCTF2019]childRSA[HDCTF2019]bbbbbbrsaRSA4[BJDCTF2020]rsa_output[BJDCTF2020]RSA[WUSTCTF2020]babyrsa[ACTF新生赛2020]crypto-rsa0[ACTF新生赛2020]crypto-rsa3[GWCTF 2019]…...
javascript与Node.js)
javascript 编程基础(2)javascript与Node.js
文章目录 一、Node.js 与 JavaScript1、基本概念1.1、JavaScript:动态脚本语言1.2、Node.js:JavaScript 运行时环境 2、核心区别3、执行环境差异3.1、浏览器中的JavaScript3.2、Node.js中的JavaScript 4、共同点5、为什么需要Node.js? 一、No…...

IDEA+AI 深度融合:重构高效开发的未来模式
在 Java 开发领域,IntelliJ IDEA(以下简称 IDEA)作为最受欢迎的集成开发环境之一,一直是开发者的得力工具。而飞算 JavaAI 凭借强大的人工智能技术,为 Java 开发带来了全新的效率提升可能。当 IDEA 与飞算 JavaAI 深度…...

深度学习中常见损失函数激活函数
损失函数 一、分类任务损失函数 二、回归任务损失函数 三、生成对抗网络(GAN)损失函数 四、其他专用损失函数 五、损失函数选择原则 任务类型:分类用交叉熵,回归用MSE/MAE。 数据分布:类别不平衡时选择Focal Loss或…...

入职软件开发与实施工程师了后........
时隔几个月没有创作的我又回来了,这几个月很忙,我一直在找工作,在自考(顺便还处理了一下分手的事),到处奔波,心力交瘁。可能我骨子里比较傲吧。我不愿意着急谋生,做我不愿意做的普通…...
)
告别Spring AI!我的Java轻量AI框架实践(支持多模型接入|注解式MCP架构|附开源地址)
~犬📰余~ “我欲贱而贵,愚而智,贫而富,可乎? 曰:其唯学乎” 1. 开发初衷 \quad 大家好,我是犬余,之前,为了体验一下MCP架构的JAVA实现,犬余使用了Spring AI框…...

【软考-架构】15、软件架构的演化和维护
✨资料&文章更新✨ GitHub地址:https://github.com/tyronczt/system_architect 文章目录 软件架构演化和定义面向对象软件架构演化软件架构演化方式的分类软件架构演化原则软件架构演化评估方法大型网站架构演化软件架构维护 软件架构演化和定义 软件架构生命周…...

编译Qt5.15.16并启用pdf模块
编译Qt5.15.16并启用pdf模块 标题1.目录设置 -q-bulid –qt-everywhere-src-5.15.16 –bulid cd bulid 必须,否则会提示Project ERROR: You cannot configure qt separately within a top-level build. create .qmake.stash and .qmake.super in build folder …...

spring中的EnvironmentPostProcessor接口详解
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站 EnvironmentPostProcessor 是 Spring Boot 提供的一个关键扩展接口,允许开发者在 Spring 应用环境初始化后、应用上下文创建前&…...

自学嵌入式 day20-数据结构 链表
注:gdb调试工具用法 3.链表的常规操作 (6)尾部插入 int InsertTailLinkList(LinkList* ll, DATATYPE* data) { if (IsEmptyLinkList(ll))//判断链表是否为空 { return InsertHeadLinkList(ll, data); } else { …...
)
Java设计模式之外观模式:从入门到精通(保姆级教程)
外观模式是结构型设计模式中非常实用的一种,它为复杂的子系统提供了一个统一的简化接口。本文将全面深入地剖析外观模式,从基础概念到高级应用,通过丰富的代码示例、图表和日常生活类比,帮助您彻底掌握这一模式。 一、外观模式基础概念 1.1 什么是外观模式? 外观模式(…...

Ubuntu 20.04 postgresql
安装命令 $ sudo apt-get update $ sudo apt-get install -y postgresql查看postgresql版本 $ psql --version psql (PostgreSQL) 12.22 (Ubuntu 12.22-0ubuntu0.20.04.3)查看系统用户组是否存在postgres $ getent group postgres postgres:x:115: $ getent passwd postgres…...

游戏引擎学习第295天:堆叠房间用于Z层调试
关于确定哪些系统影响许多其他系统,并尽早将其固定下来 目前我们的游戏开发已经进入了一个关键阶段,我们觉得是时候来彻底解决 Z(深度)相关的问题了。之前我们在 Z 轴的处理上做了一些尝试,但始终没有一个明确的定论&…...

【Python 算法零基础 4.排序 ② 冒泡排序】
目录 一、引言 二、算法思想 三、时间复杂度和空间复杂度 1.时间复杂度 2.空间复杂度 四、冒泡排序的优缺点 1.算法的优点 2.算法的缺点 五、实战练习 88. 合并两个有序数组 算法与思路 ① 合并数组 ② 冒泡排序 2148. 元素计数 算法与思路 ① 排序 ② 初始化计数器 ③ 遍历数组…...
)
【工具】Windows|外接的显示器怎么用软件调亮度(Brightness Slider)
文章目录 工具安装及使用Twinkle Tray:Brightness Slider补充背景知识1. DDC/CI(Display Data Channel Command Interface)2. WMI(Windows Management Instrumentation)3. Twinkle Tray如何结合两者?对比总…...

1.3.3 数据共享、汇聚和使用中的安全目标
探索数据共享、汇聚与使用中的安全目标 在当今数字化时代,数据的价值愈发凸显,数据共享、汇聚与使用成为了推动业务发展、促进创新的重要环节。然而,在这一过程中,数据安全至关重要,我们需要明确并保障保密性、完整性…...

【QT】类A和类B共用类C
当类A和类B需要操作同一个输入框时,需要采用共享实例的设计模式。以下是具体实现方案: 1. 核心实现思路 #mermaid-svg-cdmYFhkgOZ5C0uI5 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-cdmYF…...
》阅读笔记:p86-p90)
《算法导论(第4版)》阅读笔记:p86-p90
《算法导论(第4版)》学习第 19 天,p83-p85 总结,总计 3 页。 一、技术总结 无。 二、英语总结(生词:2) 1. inkling (1)inkling: inclen(“utter in an undertone,低声说话”) c. a hint(提示);a slight knowledg…...

AI在网络安全中的应用之钓鱼邮件检测
0x01 前言 为什么写这个呢,源自于我之前在某教培网站留了信息,不出意外的个人信息泄露的飞快,邮箱开始疯狂收到垃圾邮件甚至钓鱼邮件,看着每天的拦截消息,就在想这个拦截机制挺好玩的,拦截器是怎么知道是不…...

游戏引擎学习第294天:增加手套
准备战斗 我们正在进行的是第294天的开发,目前暂时没有特别确定要做的内容,但我们决定继续研究移动模式相关的部分。虽然一些小型实体系统已经在运行,但并不确定最终效果如何。 今天我们决定实现一个全新的功能:战斗系统。这是游…...
)
[架构之美]从PDMan一键生成数据库设计文档:Word导出全流程详解(二十)
[架构之美]从PDMan一键生成数据库设计文档:Word导出全流程详解(二十) 一、痛点 你是否经历过这些场景? 数据库字段频繁变更,维护文档耗时费力用Excel维护表结构,版本混乱难以追溯手动编写Word文档&#…...

5个开源MCP服务器:扩展AI助手能力,高效处理日常工作
AI大语言模型(如Claude、GPT)尽管强大,但其原生形态仅限于文本对话,无法直接与外部世界交互。这一局限严重制约了AI在实际应用场景中的价值发挥 - 无法主动获取实时数据、无法操作外部系统、无法访问用户私有资源。 MCPÿ…...

服务器的基础知识
什么是服务器 配置牛、运行稳、价格感人的高级计算机,家用电脑不能比拟的。 服务器的组成:电源、raid卡、网卡、内存、cpu、主板、风扇、硬盘。 服务器的分类 按计算能力分类 超级计算机 小型机AIX x86服务器(服务器cpu架构) …...
- 本地部署(前后端))
bisheng系列(二)- 本地部署(前后端)
一、导读 环境:Ubuntu 24.04、open Euler 23.03、Windows 11、WSL 2、Python 3.10 、bisheng 1.1.1 背景:需要bisheng二开商用,故而此处进行本地部署,便于后期调试开发 时间:20250519 说明:bisheng前后…...

华为ODgolang后端一面面经
MySQL死锁是怎么产生的? 假如有一条SQL语句执行了非常久,你会怎么优化呢? explain 索引什么情况下会失效? InnoDB和MyISAM引擎的区别是什么? 为什么是三次握手 避免历史连接 同步双方初始序列号避免资源浪费 为什么…...

UE5 GAS框架解析内部数据处理机制——服务器与客户端
当, gas通过点击鼠标光标触发事件时,内部的处理机制。 当通过点击事件,命中中目标时, 可获取到对应的TargetData 目标数据。处理相应的操作。 仅有本地的客户端的情况下。命中并不会有什么异常。 当存在服务器时, 服…...

《打造第二大脑》
序 第二大脑,前景无限 2025/05/08 发表想法 是的说的太对了,关键是之前自己一直在找如何能避免出现此问题的方法,今天终于看到了本书所讲的的内容 原文:我们耗费了无数的时间阅读、倾听和观摩他人提供的处世原则、思考方式以及生活…...

Word2Vec详解
目录 Word2Vec 一、Word2Vec 模型架构 (一)Word2Vec 的核心理念 (二)Word2Vec 的两种架构 (三)负采样与层次 Softmax (四)Word2Vec 的优势与局限 二、Word2Vec 预训练及数据集…...

[特殊字符] Word2Vec:将词映射到高维空间,它到底能解决什么问题?
一、在 Word2Vec 之前,我们怎么处理语言? 在 Word2Vec 出现之前,自然语言处理更多是“工程方法”,例如字符串匹配、关键词提取、正则规则...。但这些表示通常缺乏语义,词与词之间看不出任何联系以及非常浅显。当然,技术没有好坏,只有适合的场景。例如: 关键词匹配非常…...

anythingLLM支持本地大模型嵌入知识库后进行api调用
anythingLLM 可以使用本地大模型,并且可以嵌入知识库(Knowledge Base),通过 API 调用该知识库。 ✅ 一、anythingLLM 的基本架构 anythingLLM 是一个支持多种本地大模型(如 LLaMA、Qwen、ChatGLM 等)的开…...

PHP 实现连续子数组的最大和、整数中1出现的次数
在编程面试和实际应用中,处理数组和整数的常见问题之一是求解连续子数组的最大和以及计算整数中1出现的次数。本文将详细介绍如何使用 PHP 实现这两个问题的解决方案。 连续子数组的最大和 连续子数组的最大和问题要求找到一个数组中的连续子数组,使得…...

面试题之进程 PID 分配与回收算法:从理论到 Linux 内核实现
总结: 在操作系统中,进程 PID(Process Identifier)的分配与回收是核心功能之一。本文深入剖析了三种主流算法:位图法、空闲链表法和位图 哈希表组合法,并结合 Linux 内核源码探讨其优化思路。通过时间复杂…...

Pyro:基于PyTorch的概率编程框架
Pyro:基于PyTorch的概率编程框架 **Pyro:基于PyTorch的概率编程框架**基础讲解**一、Pyro核心模块****1. 入门与基础原语****2. 推理算法****3. 概率分布与变换****4. 神经网络与优化****5. 效应处理与工具库** **二、扩展应用与社区贡献****1. 特定领域…...

API Gateway REST API 集成 S3 服务自定义 404 页面
需求分析 使用 API Gateway REST API 可以直接使用 S3 作为后端集成对外提供可以访问的 API. 而当访问的 URL 中存在无效的桶, 或者不存在的对象时, API Gateway 默认回向客户端返回 200 状态码. 而实际上这并不是正确的响应, 本文将介绍如何自定义返回 404 错误页面. 基本功…...
)
02-前端Web开发(JS+Vue+Ajax)
介绍 在前面的课程中,我们已经学习了HTML、CSS的基础内容,我们知道HTML负责网页的结构,而CSS负责的是网页的表现。 而要想让网页具备一定的交互效果,具有一定的动作行为,还得通过JavaScript来实现。那今天,我们就来讲…...

visual studio code中的插件都是怎么开发的?用的什么编程语言?
目录 开发VS Code插件的编程语言 开发VS Code插件的步骤 学习资源 Visual Studio Code(VS Code)是一款流行的开源代码编辑器,由微软开发,支持多种编程语言。它的一个重要特性是可以通过插件(Extensions)来扩展其功能。这些插件可以增加新的语言支持、主题、调试器以及…...

python第30天
知识点回顾: 导入官方库的三种手段导入自定义库/模块的方式导入库/模块的核心逻辑:找到根目录(python解释器的目录和终端的目录不一致) 作业:自己新建几个不同路径文件尝试下如何导入 浙大疏锦行-CSDN博客 from lib.ut…...

【数据仓库面试题合集③】实时数仓建模思路与实践详解
实时数据仓库已经成为各大企业构建核心指标监控与业务实时洞察的基础能力。面试中,关于实时建模的题目频繁出现,尤其聚焦于建模思路、宽表设计、状态管理、乱序处理等方面。本文整理典型题目及答题思路,帮助你应对相关考察。 一、建模原则与数仓分层认知 1. 实时数仓与离线…...

kotlin Android AccessibilityService 无障碍入门
安卓的无障碍模式可以很好的进行自动化操作以帮助视障人士自动化完成一些任务。 无障碍可以做到,监听屏幕变化,朗读文本,定位以及操作控件等。 以下从配置到代码依次进行无障碍设置与教程。 一、配置 AndroidManifest.xml 无障碍是个服务…...
:最小可行化产品(MVP)的设计、验证与数据驱动迭代)
精益数据分析(69/126):最小可行化产品(MVP)的设计、验证与数据驱动迭代
精益数据分析(69/126):最小可行化产品(MVP)的设计、验证与数据驱动迭代 在创业旅程中,从需求洞察到产品落地的关键一跃是打造最小可行化产品(MVP)。今天,我们结合《精益…...

JVM频繁FullGC:面试通关“三部曲”心法
想象一下,你的Java应用程序是一个繁忙的工厂,JVM堆内存就是工厂的仓库和车间。垃圾收集(GC)就像工厂的清洁工,负责清理不再需要的废料(无用对象),腾出空间让新的生产(对象…...

Scala语言基础与函数式编程详解
Scala语言基础与函数式编程详解 本文系统梳理Scala语言基础、函数式编程核心、集合与迭代器、模式匹配、隐式机制、泛型与Spark实战,并对每个重要专业术语进行简明解释,配合实用记忆口诀与典型代码片段,助你高效学习和应用Scala。 目录 Scal…...

大语言模型 13 - 从0开始训练GPT 0.25B参数量 MiniMind2 补充 训练开销 训练步骤 知识蒸馏 LoRA等
写在前面 GPT(Generative Pre-trained Transformer)是目前最广泛应用的大语言模型架构之一,其强大的自然语言理解与生成能力背后,是一个庞大而精细的训练流程。本文将从宏观到微观,系统讲解GPT的训练过程,…...

【NLP】37. NLP中的众包
众包的智慧:当“无数人”帮你训练AI 当我们谈论构建大语言模型时,脑海中浮现的往往是服务器、GPU 和Transformer,而很少想到成千上万的普通人也在默默贡献力量。 这背后依赖的机制就是:众包(Crowdsourcing࿰…...

数据分析入门指南:从历史到实践
在信息爆炸的时代,数据分析已经成为各行各业不可或缺的技能,无论是商业决策、医疗研究,还是社会科学,数据分析都在其中扮演着关键角色。本文将带你深入了解数据分析的历史、定义、流程、数据来源与处理、常用工具,并通…...

大语言模型 12 - 从0开始训练GPT 0.25B参数量 MiniMind2 补充 训练开销 训练步骤 知识蒸馏 LoRA等
写在前面 GPT(Generative Pre-trained Transformer)是目前最广泛应用的大语言模型架构之一,其强大的自然语言理解与生成能力背后,是一个庞大而精细的训练流程。本文将从宏观到微观,系统讲解GPT的训练过程,…...
:数据透视表实战与解决方案验证——从问卷分析到产品落地的关键跨越)
精益数据分析(68/126):数据透视表实战与解决方案验证——从问卷分析到产品落地的关键跨越
精益数据分析(68/126):数据透视表实战与解决方案验证——从问卷分析到产品落地的关键跨越 在创业的移情阶段,通过问卷调查获取数据后,如何深入分析数据并验证解决方案的可行性?今天,我们结合《…...

Cursor 模型深度分析:区别、优缺点及适用场景
Cursor 模型深度分析:区别、优缺点及适用场景 在AI辅助编程领域,Cursor凭借其多模型架构和智能上下文感知能力,成为开发者提升效率的核心工具。不同模型在代码生成、逻辑推理、多模态处理等方面存在显著差异,本文将结合技术特性与…...

LightRAG 由入门到精通
LightRAG 由入门到精通 作者:王珂 邮箱:49186456qq.com 文章目录 LightRAG 由入门到精通简介一、LightRAG Server1.1 安装 LightRAG Server1.2 LightRAG Server 和 WebUI1.2.1 配置 LightRAG Server1.2.2 启动 LightRAG Server1.2.3 使用 Docker 加载 …...

【Spring Boot 整合 MongoDB 完整指南】
目录 Spring Boot 整合 MongoDB 完整指南1. 添加依赖2. 配置 MongoDB 连接application.properties 方式:application.yml 方式:3. 创建实体类(映射MongoDB中的文档,相当于MySQL的表)4. 创建 Repository 接口完成简单操作5. 使用 MongoTemplate 进行复杂操作6. 高级配置配置…...
