当前位置：首页 > news >正文

最小二乘法拟合直线，用线性回归法、梯度下降法实现

news 来源：原创 2025/6/11 9:30:42

参考笔记：

最小二乘法拟合直线，多个方法实现-CSDN博客

一文让你彻底搞懂最小二乘法（超详细推导）-CSDN博客

1.问题引入

2.线性回归法

2.1 模型假设

2.2 定义误差函数

2.3 求偏导并解方程

2.4 案例实例

2.4.1 手工计算实例

2.4.2 使用Python实现

3.梯度下降法

3.1 前言（梯度下降算法原理介绍）

3.2 模型假设

3.3 定义损失函数

3.4 梯度计算

3.5 更新参数

3.6 代码演示

4.其他方法

1.问题引入

在数据分析问题中，常常需要通过 n 组二维数据点 $\color{red}(x_1,y_1),(x_2,y_2)....(x_n,y_n)$ 拟合出一条直线 $y={\color{red}a}x+\color{red}b$ ，其中斜率 a、截距 b 是未知参数，如下图所示：

那为什么要说拟合呢？这是因为我们无法找到一条直线经过所有的点，也就是说方程无确定解

于是这就是我们引出了要解决的问题：虽然没有确定解，但是我们能不能求出近似解，即拟合出一条直线，使得这条直线能最佳地反映数据点的整体趋势

那么问题又来了， "最佳的准则" 是什么呢？可以是所有数据点到直线的距离总和最小，也可以是所有数据点到直线的误差（真实y值 - 拟合y值）绝对值总和最小，也可以是其他。如果是你面临这个问题你会怎么选择？

早在 19 世纪，勒让德就认为让 "误差的平方和最小" 拟合出来的直线是最接近真实情形的

为什么是 "误差的平方和" 而不是其它的，这个问题连欧拉、拉普拉斯都未能成功回答，后来是高斯建立了一套误差分析理论，从而证明了确实是使 "误差的平方和最小" 的情况下系统是最优的。这个我们就无需深究了

按照勒让德的 "误差的平方和最小" 最佳原则，于是就是求：

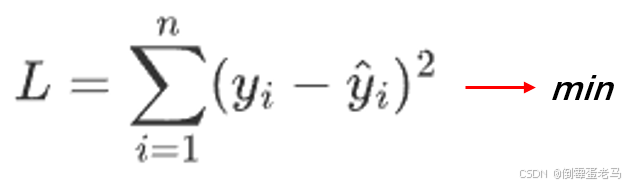
$y_i$ ：真实 y 值 $\hat y_i$ ：拟合 y 值

拟合一条直线 $y={\color{red}a}x+\color{red}b$ ，其实就是找最优斜率 a 、最优截距 b 的过程，所以我们可以通过上面的 L 函数，在其取得最小值 min 时得到的 a、b 即为最优解，这样拟合出了 n 组数据点 $\color{red}(x_1,y_1),(x_2,y_2)....(x_n,y_n)$ 的最佳直线

这就是最小二乘法的思想，所谓 "二乘" 就是平方的意思

至于怎么求出具体的 a、b，理论上可以用：

① 线性回归法

② 梯度下降法：就是模型训练，把 L 作为损失函数即可

③ .....

下面我们就以最常用的线性回归、梯度下降法为例进行推导和求解

2.线性回归法

线性回归法也称为直接法，计算简单，可以直接推导出拟合直线 $y={\color{red}a}x+\color{red}b$ 的 $\color{red}a,b$ ，而且许多非线性的问题也可以转化为线性问题来解决，所以得到了广泛的应用

2.1 模型假设

假设我们有 n 组二维数据点 $\color{red}(x_1,y_1),(x_2,y_2)....(x_n,y_n)$ ，我们的目标是找到一条直线 $y={\color{red}a}x+\color{red}b$ ，其中 a 为直线斜率，b为截距，使得这条直线尽可能接近所有数据点

2.2 定义误差函数

对于每个数据点 $\color{red}(x_i,y_i)$ ，预测值为 $\hat y_i = ax_i+b$ ，则误差为：

$e_i = y_i - \hat y_i = y_i - (ax_i+b)$

目标：最小化所有数据点的误差平方和：

最终目标就是找到使总误差 S 最小的 a、b，这可以通过 S 分别对 a、b 求偏导，并令偏导数 = 0 来实现

2.3 求偏导并解方程

为了找到使总误差 S 最小的 a、b，可以对 a 和 b 分别求偏导，令导数为 0 ，得到方程组如下：

整理后得到如下方程：

注： $\sum = \sum_{i=1}^n$

通过代数运算消元，解得：

🆗，这样就能拟合出有 n 组二维数据点 $\color{red}(x_1,y_1),(x_2,y_2)....(x_n,y_n)$ 的一条直线 $y={\color{red}a}x+\color{red}b$ 。可以看到，整个过程非常简单，只需要数学计算即可

2.4 案例演示

2.4.1 手工计算实例

假设有以下数据点：

$(1,2),(2,3),(3,5),(4,4)$

计算中间项：

代入公式：

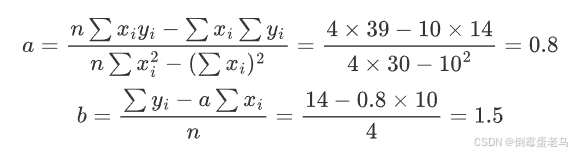
拟合直线：

$y={\color{red}0.8} \;x+\color{red}1.5$

2.4.2 使用Python实现

我们将 2.4.1 中的手工计算例子使用 Python 来实现，并作可视化

import numpy as np
import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"] = ["SimHei"]  #设置字体，可以显示中文
plt.rcParams["axes.unicode_minus"] = False  # 正常显示负号# 1. 生成数据
x = np.array([1, 2, 3, 4])
y = np.array([2, 3, 5, 4])# 2. 最小二乘法实现
def linear_regression(x, y):"""最小二乘法线性回归参数:x: 数据点的x坐标值y: 数据点的y坐标值返回:(a, b): 斜率，截距"""n = len(x)sum_x = np.sum(x)sum_y = np.sum(y)sum_x2 = np.sum(x ** 2)sum_xy = np.sum(x * y)# 计算斜率a = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x ** 2)b = (sum_y - a * sum_x) / nreturn (a, b)#执行回归计算，a：拟合出来的斜率 b：拟合出来的截距
a, b = linear_regression(x, y)# 3. 可视化结果
plt.figure(figsize=(10, 6), dpi=100)#绘制数据点
plt.scatter(x, y,color='steelblue',  # 点颜色s=90,  # 点大小edgecolor='white',  # 边缘颜色linewidth=1.5,  # 边缘线宽label='数据点',zorder=1)  # 绘制层级#绘制拟合直线
x_fit = np.array([min(x) - 1, max(x) + 1])  # 延长拟合线范围
y_fit = a * x_fit + b
plt.plot(x_fit, y_fit,color='crimson',linewidth=3,label=f'拟合结果 ($y={a:.2f}x + {b:.2f}$)',zorder=1)#添加图表元素
plt.title('最小二乘法线性回归演示', fontsize=14, pad=20)
plt.xlabel("X 值", fontsize=12)
plt.ylabel("Y 值", fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(fontsize=12, frameon=True, shadow=True)# 设置坐标轴范围
plt.xlim(min(x) - 1, max(x) + 1)
plt.ylim(min(y) - 2, max(y) + 2)# 显示图表
plt.tight_layout()
plt.show()

运行结果：

3.梯度下降法

3.1 前言（梯度下降算法原理介绍）

梯度下降（Gradient Descent）是一种迭代优化算法，通过不断沿损失函数负梯度方向更新参数，逐步逼近最优解。对于线性回归问题，需最小化均方误差（MSE）：

其中 $\color{red}a$ 为斜率， $\color{red}b$ 为截距

3.2 模型假设

假设我们有 n 组二维数据点 $\color{red}(x_1,y_1),(x_2,y_2)....(x_n,y_n)$ ，我们的目标是找到一条直线 $y={\color{red}a}x+\color{red}b$ ，其中 a 为直线斜率，b 为截距，使得这条直线尽可能接近所有数据点

3.3 定义损失函数

对于每个数据点 $\color{red}(x_i,y_i)$ ，我们希望拟合的直线为 $y={\color{red}a}x+\color{red}b$
定义预测值为： $\hat y_i = ax_i+b$
定义平方误差项为： $e_i^2=(y_i-\hat y_i)^2 = (y_i-(ax_i+b))^2$
总的误差平方和（损失函数）为：

3.4 梯度计算

为了使用梯度下降法，需要计算损失函数 $\color{red}J(a,b)$ 对参数a和b的偏导数（梯度）:

对 a 的偏导数：

对 b 的偏导数：

3.5 更新参数

通过梯度下降法，我们可以更新参数 a、b，使其朝着减少损失函数的方向移动。更新规则为：

其中 $\color{red}\alpha$ 为学习率，控制更新步长

重复计算梯度并更新参数，直到达到预设的迭代次数或损失函数的变化小于某个阈值

理论上，随着迭代次数的增加，损失函数 $\color{red}J(a,b)$ 会逐渐减小，最终收敛到损失函数的局部最小值，得到最佳的斜率 a、截距 b

🆗，以上就是梯度下降法的整个流程，下来我们会用 Python 举一个案例并作可视化

3.6 代码演示

import numpy as np
import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"] = ["SimHei"]  #设置字体，可以显示中文
plt.rcParams["axes.unicode_minus"] = False  # 正常显示负号# 固定随机种子保证可重复性
np.random.seed(42)# 生成模拟数据
# 生成100个[0-10]区间均匀分布的值，作为数据点的x坐标值
x = np.linspace(0, 10, 100)# 生成理想的线性关系： y = 2.5x + 1.8
true_a = 2.5  #真实斜率
true_b = 1.8  #真实截距
y = true_a * x + true_b# 添加高斯噪声来模拟真实数据
noise = np.random.normal(0,2,size=len(x))
y = y + noise #作为数据点的y坐标点# 梯度下降参数
alpha = 0.01  # 学习率
iterations = 2000  # 迭代次数# 参数初始化
a, b = 0.0, 0.0
n = len(x)# 记录训练过程
history = {'a': [], 'b': [], 'loss': []}# 梯度下降迭代
for i in range(iterations):# 预测值y_pred = a * x + b# 计算梯度grad_a = (-2 / n) * np.sum(x * (y - y_pred))grad_b = (-2 / n) * np.sum(y - y_pred)# 更新参数a -= alpha * grad_ab -= alpha * grad_b# 记录损失值loss、参数a、参数bloss = (1/n) * np.sum((y - y_pred) ** 2)history['a'].append(a)history['b'].append(b)history['loss'].append(loss)# 最终结果
print(f"真实参数: a={true_a}, b={true_b}")
print(f"拟合结果: a={a:.2f}, b={b:.2f}")# 可视化
plt.figure(figsize=(12, 4))# 损失函数下降曲线
plt.subplot(131)
plt.plot(history['loss'], color='darkorange')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Loss Function Convergence(损失函数下降曲线)')# 参数变化轨迹
plt.subplot(132)
plt.plot(history['a'], history['b'], marker='o', markersize=2)
plt.xlabel('a')
plt.ylabel('b')
plt.title('Parameter Trajectory(参数变化轨迹)')# 最终拟合效果
plt.subplot(133)
plt.scatter(x, y, alpha=0.6, label='数据点')
plt.xlabel('X')
plt.ylabel('Y')
plt.plot(x, a * x + b, color='crimson', lw=3,label=f'拟合结果: y={a:.2f}x + {b:.2f}')
plt.plot(x, true_a * x + true_b, 'k--', label=f'True: y={true_a:.2f}x + {true_b:.2f}')
plt.title('最小二乘法梯度下降演示')plt.legend()
plt.tight_layout()
plt.show()

运行结果：

可以看到，经过 2000 次的迭代，最终的拟合结果是 $y={\color{red}2.53}\;x+\color{red}1.45$ ，非常接近 True

🆗，以上就是本文最小二乘法拟合直线的所有内容，后续如果学习到其他方法还会继续更新，整个流程走下来感觉还是挺有趣的

4.其他方法

待更新....

1.问题引入

2.线性回归法

2.1 模型假设

2.2 定义误差函数

2.3 求偏导并解方程

2.4 案例演示

2.4.1 手工计算实例

2.4.2 使用Python实现

3.梯度下降法

3.1 前言（梯度下降算法原理介绍）

3.2 模型假设

3.3 定义损失函数

3.4 梯度计算

3.5 更新参数

3.6 代码演示

4.其他方法

相关文章：