当前位置：首页 > news >正文

【深度学习】#11 优化算法

news 来源：原创 2025/6/17 19:59:33

主要参考学习资料：

《动手学深度学习》阿斯顿·张等著

【动手学深度学习 PyTorch版】哔哩哔哩@跟李牧学AI

深度学习中的优化挑战
- 局部极小值
- 鞍点
- 梯度消失
凸性
- 凸集
- 凸函数
梯度下降
- 一维梯度下降
- - 学习率
  - 局部极小值
- 多元梯度下降
随机梯度下降
- 随机梯度更新
- 动态学习率
- 小批量随机梯度下降
动量法
AdaGrad算法
RMSProp算法
Adadelta算法
Adam算法
学习率调度器
- 因子调度器
- 多因子调度器
- 余弦调度器
- 预热

概述

深度学习的优化挑战主要有局部极小值、鞍点和梯度消失。
凸性可作为测试优化算法效果的一种简单情况。
梯度下降是优化算法的一个理论核心兼最基础的方法。
随机梯度下降和小批量随机梯度下降提高了梯度计算的效率。
动量法综合利用过往的梯度记录更新参数。
AdaGrad、RMSProp、AdaDelta、Adam算法根据梯度大小采用自适应学习率。
学习率调度器根据训练进度动态调整学习率。

优化算法使我们能够更新模型参数，并使损失函数的值最小化。优化算法对于深度学习非常重要，一方面，优化算法的性能直接影响模型的训练效率；另一方面，了解不同优化算法的原则及其超参数的作用将使我们能够以有针对性的方式调整超参数，以提高深度学习模型的性能。

深度学习中的优化挑战

局部极小值

对于任何目标函数 $f (x)$ ，如果在 $x$ 点对应的 $f (x)$ 值小于在 $x$ 附近任意其他点的 $f (x)$ 值，那么 $f (x)$ 可能是局部极小值。如果 $f (x)$ 在 $x$ 点的值是整个域中目标函数的最小值，那么 $f (x)$ 是全局最小值。考虑函数 $f(x)=x\cos(\pi x)(-1\leqslant x\leqslant2)$ ，其局部极小值和全局最小值如下：

深度学习模型的目标函数通常有许多局部最优解。当优化问题的数值解接近局部最优解时，随着目标函数解的梯度接近或变为零，通过最终迭代获得的数值解可能仅使目标函数局部最优，而不是全局最优。只有一定程度的噪声才可能会使参数跳出局部极小值。

鞍点

鞍点是指函数的所有梯度都消失但既不是全局最小值也不是局部极小值的任何位置。考虑函数 $f(x)=x^3$ ，它的一阶和二阶导数在 $x = 0$ 时消失：

较高维度的鞍点更加隐蔽，考虑函数 $f(x,y)=x^2-y^2$ ，它的鞍点为 $(0, 0)$ ：

梯度消失

梯度消失是可能遇到的最隐蔽的问题。考虑激活函数 $f(x)=\tanh(x)$ ，如果我们恰好从梯度接近零的 $x = 4$ 处开始优化，则在取得进展之前，优化将会停滞很长一段时间：

凸性

凸性在优化算法的设计中起到至关重要的作用，这主要是由于在这种情况下对算法进行分析和测试比较容易。如果算法在凸性条件下的效果很差，通常也很难在其他条件下得到比其更好的效果。即使深度学习中的优化问题通常是非凸的，它们也经常在其局部极小值附近表现出一些凸性。

凸集

凸集是凸性的基础。简单地说，给定向量空间中的一个集合 $X$ ，对于任何 $a,b\in X$ ，如果连接 $a$ 和 $b$ 的线段也位于 $X$ 中，则该集合是凸的。在数学表示上，这意味着对于所有的 $\lambda\in[0,1]$ ，我们有

$\lambda a+(1-\lambda)b\in X,当a,b\in X$

其中 $\lambda a+(1-\lambda)b$ 可以表示线段 $ab$ 上的所有点。

以下三个集合中，第一组是非凸的，第二、第三组是凸的：

上图从直观上也很容易用“凸出来”“凹进去”这样的形容来区分凸和非凸集合。

凸函数

有了凸集，可以引入凸函数 $f$ 。给定一个凸集 $X$ ，如果对于所有 $x,x'\in X$ 和所有 $\lambda\in[0,1]$ ，函数 $f:X\leftarrow\mathbb R$ 是凸的，则说明

$\lambda f(x)+(1-\lambda)f(x')\geqslant f(\lambda x+(1-\lambda)x')$

简单地说， $f$ 的函数曲线上任意两点的连线均在两点间函数曲线的上方，即函数曲线是向下凸的。凸集 $X$ 保证了不等式右侧是有定义的。以下三个函数中，第二个函数（余弦函数）是非凸的，第一（抛物线函数）、第三（指数函数）个函数是凸的。

梯度下降

一维梯度下降

对于一个连续可微实值函数 $f:\mathbb R\leftarrow\mathbb R$ ，一维梯度下降的更新方法如下：

$x\leftarrow x-\eta f'(x)$

其中固定步长 $\eta>0$ 。

要证明该算法的有效性，可先对 $f (x)$ 进行一阶泰勒展开得到

$f(x+\epsilon)=f(x)+\epsilon f'(x)+O(\epsilon^2)$

取 $\epsilon=-\eta f'(x)$ ，将其代入上式可得

$f(x-\eta f'(x))=f(x)-\eta f'^2(x)+O(\eta^2f'(x)^2)$

只要令 $\eta$ 小到足以使高阶无穷小项变得不相关，就有

$\eta f'(x)) \lessapprox f(x)$

这意味着一维梯度下降可以迭代 $x$ 使 $f (x)$ 的值减小。

学习率

学习率 $\eta$ 决定目标函数能否收敛到局部极小值，以及何时收敛到极小值。太小的学习率将导致 $x$ 的更新非常缓慢，需要更多的迭代：

相反，过高的学习率会使一阶泰勒展开式中的高阶无穷小项可能太大，此时 $x$ 的迭代不能保证减小 $f (x)$ 的值（下图橙点随着迭代向上以越来越大的幅度振荡）：

局部极小值

在非凸函数中，不科学的学习率将导致较差的局部极小值：

多元梯度下降

现在考虑 $\mathbf x=[x_1,\cdots,x_d]^\top$ 的情况，此时目标函数 $f:\mathbb R^d\leftarrow\mathbb R$ 将向量映射成标量。相应地，它的梯度也是一个由 $d$ 个偏导数组成的向量

$\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top$

则多元梯度下降的更新方式为

$\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x})$

下图展示了以一个较小的学习率 $\eta$ 进行二元梯度下降的效果（蓝色为等高线，橙点向较低的区域收敛，最低点为 $(0, 0)$ ）：

随机梯度下降

随机梯度更新

在深度学习中，目标函数通常是训练集中每个样本的损失函数的平均值。给定 $n$ 个样本及其对应的损失函数 $f_i(\mathbf x)$ ，则目标函数为

$f(\mathbf x)=\frac1n\sum^n_{i=1}f_i(\mathbf x)$

对应的梯度计算公式为

$\nabla f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x})$

若使用普通的梯度下降，则每个自变量迭代的计算复杂度为 $O (n)$ ，当训练集较大时，每次迭代的梯度下降计算复杂度将更高。

随机梯度下降（SGD）在每次迭代中等概率随机抽取一个索引为 $i$ 的样本来计算梯度 $\nabla f_i(\mathbf x)$ 以更新 $\mathbf x$

$\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f_i(\mathbf{x})$

该算法使得每次迭代的计算复杂度从 $O (n)$ 下降至 $O (1)$ ，并且随机梯度是对完整梯度的无偏估计，因为

$\mathbb{E}_i \nabla f_i(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}) = \nabla f(\mathbf{x})$

下图展示了随机梯度下降的效果：

由图可见，随机梯度下降的轨迹要嘈杂得多。即使接近极小值，随机梯度下降仍然受到 $\eta\nabla f_i(\mathbf x)$ 的瞬间梯度所注入的不确定性的影响。唯一改善上述问题的选择是改变学习率 $\eta$ 。太低的学习率将抑制一开始取得的进展，太高的学习率将无法收敛到一个好的解决方案，解决这一矛盾的唯一方法是在优化过程中动态降低学习率。

动态学习率

动态调整学习率的操作被称为学习率调度，它用与时间相关的学习率函数 $\eta(t)$ 取代常量 $\eta$ 。学习率函数通常是衰减的以确保收敛性，而我们需要弄清 $\eta$ 的衰减速度。衰减太快将过早停止优化，衰减太慢将在优化上浪费太多时间。以下是 $\eta(t)$ 的一些基本策略（更高级的策略将在后文讨论）

$\begin{split} \eta(t) &= \eta_i( t_i \leqslant t < t_{i+1}) \text{分段常数} \\ \eta(t) &= \eta_0 \cdot e^{-\lambda t} \text{指数衰减} \\ \eta(t) &= \eta_0 \cdot (\beta t + 1)^{-\alpha} \text{多项式衰减} \end{split}$

分段常数在不同的训练区间人为设定一系列递减的学习率常数。指数衰减使得学习率更积极地衰减，但往往会导致算法在收敛之前过早停止。一个受欢迎的选择是 $\alpha=0.5$ 的多项式衰减，在凸优化情况下表现良好。

下图展示了指数衰减的优化效果，可见该算法中参数的方差大大减小，但未能收敛到最优解 $(0, 0)$ ：

而 $\alpha=0.5$ 的多项式衰减则得到了正确的收敛：

小批量随机梯度下降

计算所有样本的梯度会使得计算复杂度较高，而只选取一个样本计算梯度又无法完全利用GPU的硬件资源。一个折中方案是小批量随机梯度下降，它在时间 $t$ 采样索引的一个随机子集 $B_t\subset\{1,\cdots,n\}$ 来计算梯度

$\mathbf x_t\leftarrow\mathbf x_{t-1}-\frac{\eta_t}{|B_t|}\sum_{i\in I_t}\nabla f_i(\mathbf x_{t-1})$

同样地，这也是一个无偏估计，且相较于随机梯度下降降低了方差。

在并行计算资源范围内，更大的批量在一次遍历中的收敛速度更慢（参数更新次数少），但耗时更短，因为GPU的每次计算都存在加载模型参数、输入数据到显存等固定开销，频繁更新将导致有效计算比例降低。

下图展示了梯度下降（GD）、随机梯度下降（SGD）、批量大小分别为10和100的小批量随机梯度下降的优化效果：

折线的一个拐点代表一次更新，两个拐点的横坐标间隔为一次迭代的耗时（对数坐标）。

动量法

目前所介绍的梯度下降都只根据当前时间步计算的梯度来更新参数，这使得梯度的大小和方向在更新过程中可能会频繁变化，降低其收敛速度。

动量法（Momentum）则将过去的梯度以一定的权重累加，使得当前参数的更新受到过去梯度值的影响。对于在时间步 $t - 1$ 更新的权重 $\mathbf w_{t-1}$ ，我们记在时间步 $t$ 中的小批量随机梯度下降为

$\mathbf g_{t}=\frac1{|B_t|}\sum_{i\in B_t}\nabla f(\mathbf x_i,\mathbf w_{t-1})$

则动量法使用超参数 $\beta\in(0,1)$ 对所有过去梯度累加得到在时间步 $t$ 的动量

$\mathbf v_t=\sum^{t}_{\tau=0}\beta^\tau\mathbf g_{t-\tau}$

其中每个时间步的梯度被赋予的权重 $\beta^\tau$ 随着到当前时间步的距离 $\tau$ 的增大而递减。上式还可写为如下递归形式

$\mathbf v_t=\beta\mathbf v_{t-1}+\mathbf g_{t}$

通俗地讲，动量法相当于为梯度下降的过程引入了“惯性”，从而具有以下优点：

在梯度方向频繁变化的区域缓解梯度振荡。
在梯度方向稳定的维度上，速度会不断累积加快收敛。
依靠速度累积更有可能逃脱鞍点和局部极小值。

最终，动量法使用如下更新公式

$\begin{split} \mathbf{v}_t &\leftarrow \beta \mathbf{v}_{t-1} + \mathbf{g}_{t}, \\ \mathbf{x}_t &\leftarrow \mathbf{x}_{t-1} - \eta_t \mathbf{v}_t. \end{split}$

对于 $\beta=0$ ，动量法相当于常规的梯度下降。 $\beta$ 越大，惯性越强，参数更新对噪声越不敏感，也越适用于崎岖地形。

下图从左到右分别展示了随机梯度下降、设置 $\beta$ 为 $0.5$ 和 $0.25$ 的动量法的优化效果，最小值点为 $(0, 0)$ ：

可以看到， $\beta=0.5$ 的动量法收敛速度最快，而 $\beta=0.25$ 的情况虽然振荡较为明显，但是整体收敛速度和最终收敛点均优于随机梯度下降。

AdaGrad算法

AdaGrad算法在梯度更新中动态调整学习率的衰减速度，其核心思想为：

在梯度较大的地方，梯度下降容易更新过猛产生振荡，应当使学习率衰减得更快。
在梯度较小的地方，梯度下降的收敛速率慢，应当抑制学习率的衰减。

该算法通过对过去梯度平方（本文对向量的平方操作默认为按元素平方）的累加来控制学习率的衰减，对于时间步 $t$ 的小批量随机梯度下降 $\mathbf g_t$ 有

$\mathbf s_t=\mathbf s_{t-1}+\mathbf g_t^2$

则参数更新公式为

$\mathbf{x}_t = \mathbf{x}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \odot \mathbf{g}_t$

其中 $\epsilon$ 是一个防止分母为零的小常量。由此可以使学习率在当前时间步的梯度更大时以更快的速度衰减。

下图展示了 $\eta$ 分别为 $0.4$ 和 $2$ 的AdaGrad算法的优化效果：

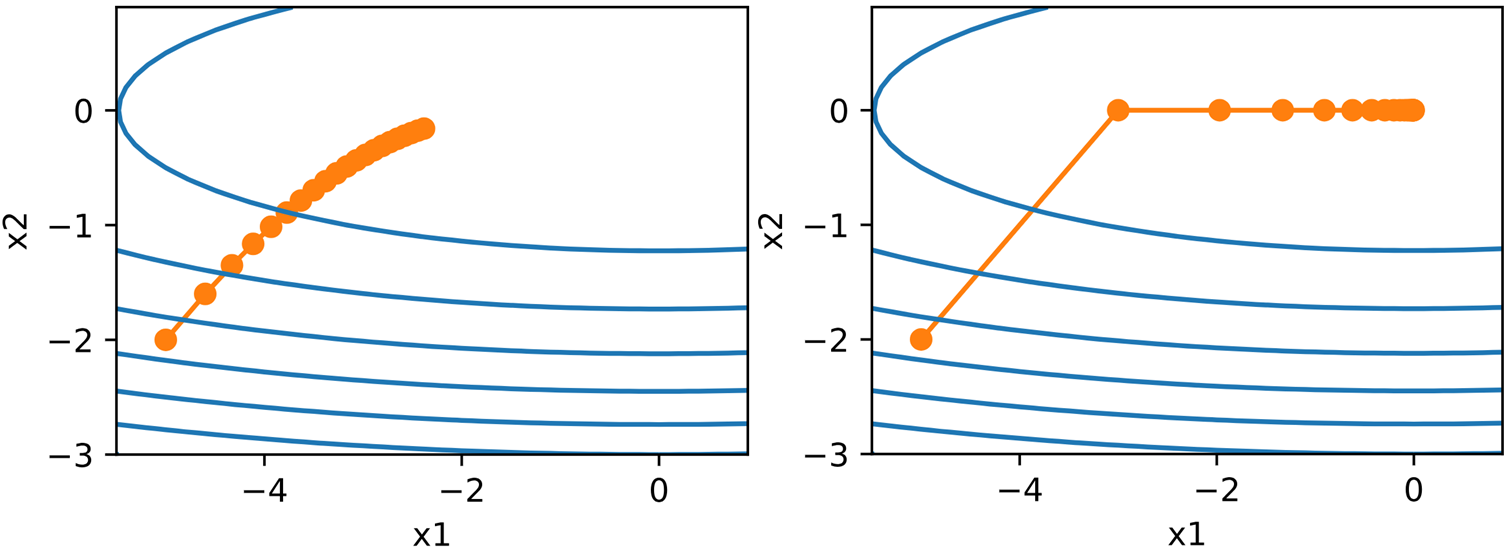
由此可见，AdaGrad算法使得我们在一开始可以大胆地选择更高的学习率以加快收敛速度，但对于较小的初始学习率，由于AdaGrad算法只能让其不断衰减，会使得后期收敛趋于停滞，这导致其仅适用于解决凸优化问题，而在非凸问题上并不理想。

RMSProp算法

造成AdaGrad算法的缺陷的一个关键因素是缺乏对 $\mathbf s_t$ 的规范化，使学习率的衰减速度几乎在收敛过程中呈线性增长。RMSProp算法从这一方面入手，保持其他部分不变，而在 $\mathbf s_t$ 的计算上采用了指数加权移动平均（EWMA），得到的值为梯度的二阶原点矩

$\begin{split} \mathbf{s}_t & \leftarrow \gamma \mathbf{s}_{t-1} + (1 - \gamma) \mathbf{g}_t^2 \\ \mathbf{x}_t & \leftarrow \mathbf{x}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \odot \mathbf{g}_t \end{split}$

该算法使得在 $\mathbf g_t$ 分布合理的情况下， $\mathbf s_t$ 能够收敛，尽管收敛生效可能会经过较长的过程。

下图展示了 $\eta=0.4$ 的RMSProp算法的优化效果：

由此可见，和AdaGrad算法相比，RMSProp算法在一定程度上更好地控制了学习率的衰减程度，从而加快了收敛。

Adadelta算法

Adadelta算法在RMSProp算法的基础上做了进一步创新，它不需要人为设置一个学习率 $\eta$ ，而是利用过往参数变化量本身作为未来更新的基准，这个基准由另一个状态变量 $\Delta\mathbf x_t$ 存储。根据RMSProp算法，我们先有

$\mathbf{s}_t \leftarrow \gamma \mathbf{s}_{t-1} + (1 - \gamma) \mathbf{g}_t^2$

由 $\mathbf s_t$ 和 $\Delta\mathbf x_t$ 共同调整后的参数更新量 $\mathbf g'_t$ 为

$\begin{split} \mathbf{g}_t' & = \frac{\sqrt{\Delta\mathbf{x}_{t} + \epsilon}}{\sqrt{{\mathbf{s}_t + \epsilon}}} \odot \mathbf{g}_t \\ \mathbf x_t&\leftarrow\mathbf x_{t-1}-\mathbf g'_t \end{split}$

而用于下一个时间步的 $\Delta\mathbf x_{t+1}$ 则通过对 $\mathbf g'_t$ 进行EWMA得到

$\Delta \mathbf{x}_{t+1} \leftarrow \gamma \Delta\mathbf{x}_{t} + (1 - \gamma) {\mathbf{g}_t'}^2$

Adam算法

Adam算法将动量法和RMSProp算法融合到一个算法中，成为了一个更加强大和有效的优化算法。它将RMSProp算法中用于更新参数的梯度替换为通过EWMA计算的动量，因而使用了两个状态变量

$\begin{split} \mathbf{v}_t & \leftarrow \beta_1 \mathbf{v}_{t-1} + (1 - \beta_1) \mathbf{g}_t \\ \mathbf{s}_t & \leftarrow \beta_2 \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2 \end{split}$

经过实际验证，在 $\beta_1=0.9,\beta_2=0.99$ 的默认设置下，Adam算法能更好地适应大量深度学习问题，较高的 $\beta$ 使得优化过程更稳定，更适合长期训练，但这也同样带来了较大的初始偏差。将EWMA的递归展开，我们得到其权重和为

$\sum^t_{i=0}(1-\beta)\beta^i=(1-\beta)\frac{1-\beta^t}{1-\beta}=1-\beta^t$

当 $\beta$ 接近 $1$ 时，权重和在 $t$ 较小的时候则接近 $0$ 。又由于我们通常初始化 $\mathbf v_0=\mathbf s_0=0$ ，这使得优化的开始阶段继承得到的动量和二阶原点矩估计很小。为了让权重和保持为 $1$ ，我们需要对状态变量进一步标准化

$\begin{split} \hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_1^t}\\ \hat{\mathbf{s}}_t = \frac{\mathbf{s}_t}{1 - \beta_2^t} \end{split}$

最终Adam算法的参数更新公式为

$\mathbf x_t\leftarrow\mathbf x_{t-1}-\frac{\eta\hat{\mathbf v}_t}{\sqrt{\hat{\mathbf s}_t}+\epsilon}$

学习率调度器

和之前的自适应学习率算法不同，学习率调度器主要依赖训练进度而不是梯度计算调整学习率的大小，并且这种调整是全局共享的，而非为每个参数单独配置。学习率调度器往往与自适应算法配合使用，以充分利用学习率这一冗余超参数，进一步控制其变化规则。

因子调度器

因子调度器使用乘法衰减作为多项式衰减的替代方案

$\eta_t\leftarrow\eta_{t-1}\cdot\alpha,\alpha\in(0,1)$

为了防止学习率衰减超出合理的下限 $\eta_{\min}$ ，更新方程通常修改为

$\eta_t\leftarrow\max(\eta_{\min},\eta_{t-1}\cdot\alpha)$

因子调度器的学习率变化曲线（ $\eta_0=2,\eta_{\min}=0.01,\alpha=0.9$ ）如下图所示：

多因子调度器

多因子调度器在因子调度器的基础上选择了保持分段恒定的学习率，即只在给定的一系列特定时间步使用乘法衰减 $\eta_t\leftarrow\eta_{t-1}\cdot\alpha$ 降低学习率。

多因子调度器（ $\eta_0=0.5,\alpha=0.5$ ，以 $t = 15$ 为分段点）的学习率变化曲线如下图所示：

余弦调度器

余弦调度器利用余弦函数调整学习率，使其从初始值平滑衰减到最小值。其特点在于学习率衰减速度先慢后快再慢，在初期保持高学习率快速探索参数空间，而在后期保持低学习率进行精细调优。

余弦调度器的更新公式为

$\eta_t=\eta_T+\frac{\eta_0-\eta_T}2(1-\cos\frac tT\pi),t\in[0,T]$

其中 $\eta_0$ 为初始学习率， $\eta_T$ 为 $T$ 时刻的目标学习率。对于 $t > T$ ，学习率将固定为 $\eta_T$ 而不再调整。

余弦调度器（ $T=20,\eta_0=0.3,\eta_T=0.01$ ）的学习率变化曲线如下图所示：

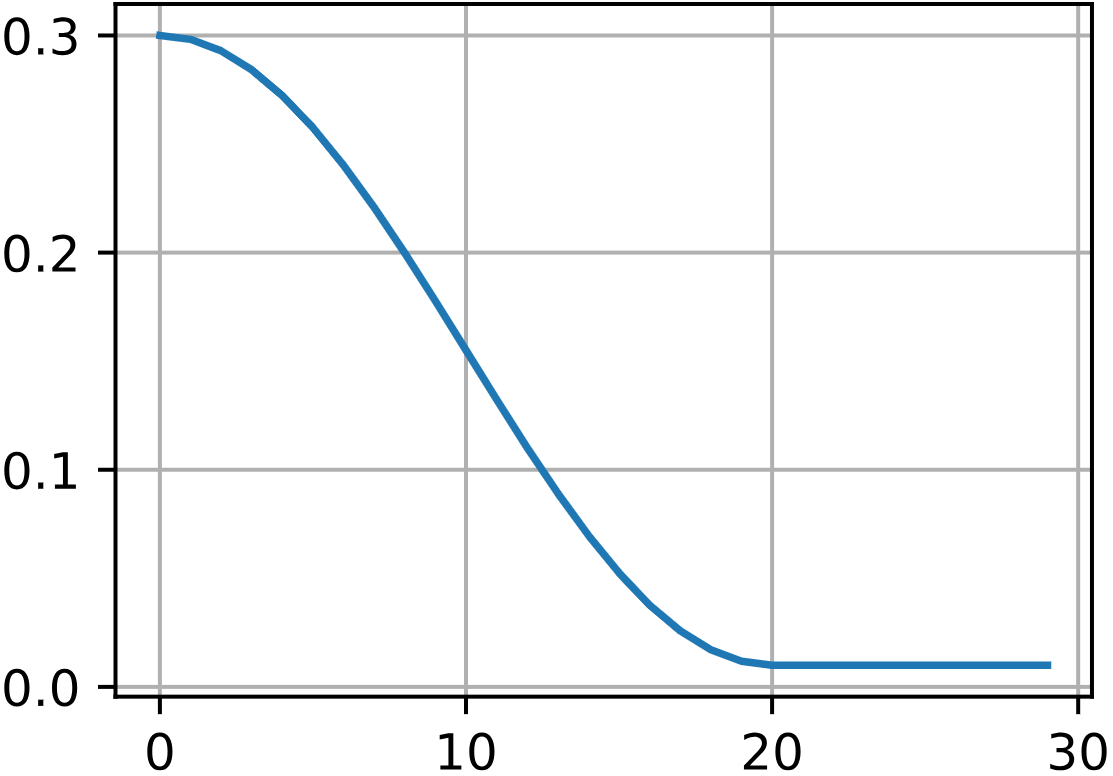
预热

某些情况下，使用较高的学习率进行初始化会导致在开始阶段就发散，而足够低的学习率又会让进展变得缓慢。解决这一问题的一个简单的方法是使用预热。在预热期间，学习率将提高至初始最大值，随后再利用学习率调度器衰减至优化过程结束。

一个在余弦调度器的基础上使用了简单线性递增来预热的学习率变化曲线如下图所示：

目录

深度学习中的优化挑战

局部极小值

鞍点

梯度消失

凸性

凸集

凸函数

梯度下降

一维梯度下降

学习率

局部极小值

多元梯度下降

随机梯度下降

随机梯度更新

动态学习率

小批量随机梯度下降

动量法

AdaGrad算法

RMSProp算法

Adadelta算法

Adam算法

学习率调度器

因子调度器

多因子调度器

余弦调度器

预热

相关文章：