【Python 算法零基础 2.模拟 ④ 基于矩阵】

目录

基于矩阵

Ⅰ、 2120. 执行所有后缀指令

思路与算法

① 初始化结果列表

② 方向映射

③ 遍历每个起始位置

④ 记录结果

Ⅱ、1252. 奇数值单元格的数目

思路与算法

① 初始化矩阵

② 处理每个操作

③ 统计奇数元素

Ⅲ、 832. 翻转图像

思路与算法

① 水平翻转图像

② 像素值取反

③ 返回结果

Ⅳ、657. 机器人能否返回原点

思路与算法

① 定义方向映射

② 初始化位置

③ 遍历移动指令

④ 判断是否回到原点

Ⅴ、 289. 生命游戏

思路与算法

① 获取矩阵尺寸

② 创建原矩阵的副本

③ 定义八个方向的偏移量

④ 遍历每个细胞

⑤ 计算活细胞邻居数量

⑥ 应用生命规则

⑦ 直接修改原矩阵

Ⅵ、59. 螺旋矩阵 II

思路与算法

① 初始化矩阵

② 初始位置与方向

③ 填充数字

④ 方向切换逻辑

⑤ 边界检查：

⑤ 终止条件：

Ⅶ、885. 螺旋矩阵 III

思路与算法

① 方向控制

② 步长规律

③ 边界检查

---

相由心生，所见都是你，一切都是自己的相

                                                               —— 25.5.14

基于矩阵

        利用矩阵的数据结构，根据题目要求，实现算法，如：

Ⅰ、 2120. 执行所有后缀指令

现有一个 n x n 大小的网格，左上角单元格坐标 (0, 0) ，右下角单元格坐标 (n - 1, n - 1) 。给你整数 n 和一个整数数组 startPos ，其中 startPos = [startrow, startcol] 表示机器人最开始在坐标为 (startrow, startcol) 的单元格上。

另给你一个长度为 m 、下标从 0 开始的字符串 s ，其中 s[i] 是对机器人的第 i 条指令：'L'（向左移动），'R'（向右移动），'U'（向上移动）和 'D'（向下移动）。

机器人可以从 s 中的任一第 i 条指令开始执行。它将会逐条执行指令直到 s 的末尾，但在满足下述条件之一时，机器人将会停止：

• 下一条指令将会导致机器人移动到网格外。
• 没有指令可以执行。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是机器人从第 i 条指令 开始 ，可以执行的 指令数目 。

示例 1：

输入：n = 3, startPos = [0,1], s = "RRDDLU"
输出：[1,5,4,3,1,0]
解释：机器人从 startPos 出发，并从第 i 条指令开始执行：
- 0: "RRDDLU" 在移动到网格外之前，只能执行一条 "R" 指令。
- 1:  "RDDLU" 可以执行全部五条指令，机器人仍在网格内，最终到达 (0, 0) 。
- 2:   "DDLU" 可以执行全部四条指令，机器人仍在网格内，最终到达 (0, 0) 。
- 3:    "DLU" 可以执行全部三条指令，机器人仍在网格内，最终到达 (0, 0) 。
- 4:     "LU" 在移动到网格外之前，只能执行一条 "L" 指令。
- 5:      "U" 如果向上移动，将会移动到网格外。

示例 2：

输入：n = 2, startPos = [1,1], s = "LURD"
输出：[4,1,0,0]
解释：
- 0: "LURD"
- 1:  "URD"
- 2:   "RD"
- 3:    "D"

示例 3：

输入：n = 1, startPos = [0,0], s = "LRUD"
输出：[0,0,0,0]
解释：无论机器人从哪条指令开始执行，都会移动到网格外。

提示：

• m == s.length
• 1 <= n, m <= 500
• startPos.length == 2
• 0 <= startrow, startcol < n
• s 由 'L'、'R'、'U' 和 'D' 组成

思路与算法

① 初始化结果列表

用于存储每个起始位置对应的可执行指令数。

② 方向映射

通过字典将方向字符映射为坐标变化量，方便后续移动计算。

③ 遍历每个起始位置

对于每个起始位置 i，重置临时计数器 tmp 和机器人的初始位置 (x, y)。从 s[i] 开始逐个执行指令：根据指令更新机器人位置。检查新位置是否越界。若越界，立即终止循环；否则计数器加一。

④ 记录结果

将每个起始位置对应的计数器值存入结果列表。

class Solution:def executeInstructions(self, n: int, startPos: List[int], s: str) -> List[int]:res = []# 定义方向矩阵dir = {"L" : (0, -1), "R" : (0, 1), "U" : (-1, 0), "D" : (1, 0)}for i in range(len(s)):tmp = 0x, y = startPos[0], startPos[1]for j in s[i:]:x = x + dir[j][0]y = y + dir[j][1]if x < 0 or y < 0 or x >= n or y >= n:breakelse:tmp += 1res.append(tmp)return res

---

Ⅱ、1252. 奇数值单元格的数目

给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

1. ri 行上的所有单元格，加 1 。
2. ci 列上的所有单元格，加 1 。

给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

示例 1：

输入：m = 2, n = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

示例 2：

输入：m = 2, n = 2, indices = [[1,1],[0,0]]
输出：0
解释：最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

提示：

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

思路与算法

① 初始化矩阵

创建一个 m 行 n 列的矩阵 matrix，所有元素初始化为 0。

② 处理每个操作

遍历 indices 中的每个操作 (x, y)，其中 x 表示行索引，y 表示列索引。

③ 统计奇数元素

遍历整个矩阵，统计值为奇数的元素个数。 

class Solution:def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:matrix = [[0] * n for _ in range(m)]  # 正确初始化m行n列的矩阵for x, y in indices:# 处理行x的所有列元素for col in range(n):matrix[x][col] += 1# 处理列y的所有行元素for row in range(m):matrix[row][y] += 1# 统计奇数数量count = 0for row in matrix:for num in row:if num % 2 != 0:count += 1return count

---

Ⅲ、 832. 翻转图像

给定一个 n x n 的二进制矩阵 image ，先 水平 翻转图像，然后 反转 图像并返回 结果 。

水平翻转图片就是将图片的每一行都进行翻转，即逆序。

• 例如，水平翻转 [1,1,0] 的结果是 [0,1,1]。

反转图片的意思是图片中的 0 全部被 1 替换， 1 全部被 0 替换。

• 例如，反转 [0,1,1] 的结果是 [1,0,0]。

示例 1：

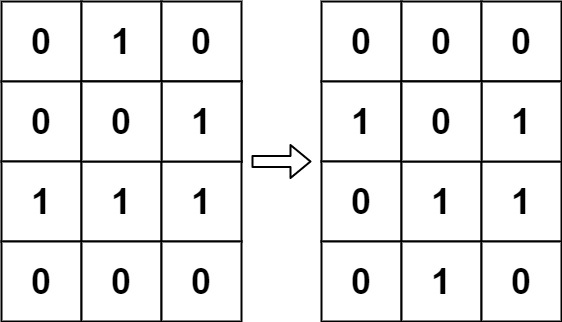
输入：image = [[1,1,0],[1,0,1],[0,0,0]]
输出：[[1,0,0],[0,1,0],[1,1,1]]
解释：首先翻转每一行: [[0,1,1],[1,0,1],[0,0,0]]；然后反转图片: [[1,0,0],[0,1,0],[1,1,1]]

示例 2：

输入：image = [[1,1,0,0],[1,0,0,1],[0,1,1,1],[1,0,1,0]]
输出：[[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
解释：首先翻转每一行: [[0,0,1,1],[1,0,0,1],[1,1,1,0],[0,1,0,1]]；然后反转图片: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]

提示：

• n == image.length
• n == image[i].length
• 1 <= n <= 20
• images[i][j] == 0 或 1.

思路与算法

① 水平翻转图像

遍历图像的每一行。对于每一行，使用切片操作 [::-1] 将该行元素反转，实现水平翻转。

② 像素值取反

再次遍历图像的每一行。对于每一行中的每个像素，检查其值。如果像素值为 0，则将其改为 1；如果像素值为 1，则将其改为 0，实现像素值取反。

③ 返回结果

经过上述两步操作后，返回处理后的图像矩阵。

class Solution:def flipAndInvertImage(self, image: List[List[int]]) -> List[List[int]]:n = len(image[0])for i in range(n):image[i] = image[i][::-1]for i in range(n):for j in range(n):if image[i][j] == 0:image[i][j] = 1else:image[i][j] = 0return image

---

Ⅳ、657. 机器人能否返回原点

在二维平面上，有一个机器人从原点 (0, 0) 开始。给出它的移动顺序，判断这个机器人在完成移动后是否在 (0, 0) 处结束。

移动顺序由字符串 moves 表示。字符 move[i] 表示其第 i 次移动。机器人的有效动作有 R（右），L（左），U（上）和 D（下）。

如果机器人在完成所有动作后返回原点，则返回 true。否则，返回 false。

注意：机器人“面朝”的方向无关紧要。 “R” 将始终使机器人向右移动一次，“L” 将始终向左移动等。此外，假设每次移动机器人的移动幅度相同。

示例 1:

输入: moves = "UD"
输出: true
解释：机器人向上移动一次，然后向下移动一次。所有动作都具有相同的幅度，因此它最终回到它开始的原点。因此，我们返回 true。

示例 2:

输入: moves = "LL"
输出: false
解释：机器人向左移动两次。它最终位于原点的左侧，距原点有两次 “移动” 的距离。我们返回 false，因为它在移动结束时没有返回原点。

提示:

• 1 <= moves.length <= 2 * 104
• moves 只包含字符 'U', 'D', 'L' 和 'R'

思路与算法

① 定义方向映射

创建字典 des，将每个移动指令（R, L, U, D）映射为对应的坐标变化量：R（右）：(1, 0) L（左）：(-1, 0) U（上）：(0, 1) D（下）：(0, -1)

② 初始化位置

将机器人的初始坐标 (x, y) 设为 (0, 0)。

③ 遍历移动指令

对于每个指令 i（如 R, L 等）：从字典 des 中获取对应的坐标变化量 (dx, dy)。更新当前坐标：x += dx, y += dy。

④ 判断是否回到原点

遍历完所有指令后，检查最终坐标 (x, y) 是否为 (0, 0)。如果是，则返回 True；否则返回 False。

class Solution:def judgeCircle(self, moves: str) -> bool:des = {"R" : (1, 0), "L" : (-1, 0), "U" : (0, 1), "D" : (0, -1)}x, y = 0, 0for i in moves:x += des[i][0]y += des[i][1]return x == y == 0

---

Ⅴ、 289. 生命游戏

根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是 同时 发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

给定当前 board 的状态，更新 board 到下一个状态。

注意 你不需要返回任何东西。

示例 1：

输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

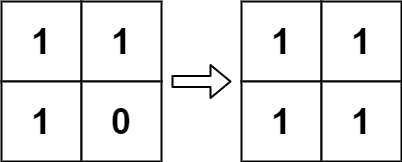
输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 25
• board[i][j] 为 0 或 1

思路与算法

① 获取矩阵尺寸

确定二维数组的大小，用于后续遍历和边界检查。

② 创建原矩阵的副本

复制原始矩阵 board 的所有值到 copy_board，确保在更新过程中使用的是原始状态，避免影响后续细胞的计算。

③ 定义八个方向的偏移量

每个元组 (dx, dy) 表示相对于当前细胞的一个方向（上、下、左、右、对角），用于遍历周围的 8 个邻居。

④ 遍历每个细胞

对矩阵中的每个细胞 (i, j) 进行处理

⑤ 计算活细胞邻居数量

对于每个细胞 (i, j)，遍历其 8 个邻居：

        计算邻居坐标 (x, y) = (i+dx, j+dy)。

        检查坐标是否越界（0 ≤ x < m 且 0 ≤ y < n）。

        若邻居在有效范围内且为活细胞（值为 1），则计数器 live_neighbors 加 1。

⑥ 应用生命规则

规则 1：活细胞周围的活邻居少于 2 个 → 死亡（孤独）。

规则 2：活细胞周围的活邻居为 2 或 3 个 → 存活（保持现状）。

规则 3：活细胞周围的活邻居多于 3 个 → 死亡（拥挤）。

规则 4：死细胞周围的活邻居恰好为 3 个 → 复活（繁殖）。

⑦ 直接修改原矩阵

所有更新直接应用到原始矩阵 board 中，符合题目 “不返回任何东西” 的要求。

class Solution:def gameOfLife(self, board: List[List[int]]) -> None:"""Do not return anything, modify board in-place instead."""m = len(board)      # 行数n = len(board[0])   # 列数# 创建一个复制数组，用于存储原始状态copy_board = [[board[i][j] for j in range(n)] for i in range(m)]# 定义8个方向的偏移量directions = [(-1,-1), (-1,0), (-1,1), (0,-1), (0,1), (1,-1), (1,0), (1,1)]# 遍历每个细胞for i in range(m):for j in range(n):# 计算周围活细胞的数量live_neighbors = 0for dx, dy in directions:x = i + dxy = j + dy# 检查邻居是否在有效范围内并且是活细胞if 0 <= x < m and 0 <= y < n and copy_board[x][y] == 1:live_neighbors += 1# 应用生命游戏规则if copy_board[i][j] == 1:if live_neighbors < 2 or live_neighbors > 3:board[i][j] = 0else:if live_neighbors == 3:board[i][j] = 1

---

Ⅵ、59. 螺旋矩阵 II

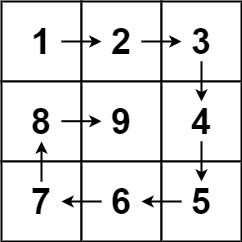
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

思路与算法

① 初始化矩阵

创建一个 n×n 的零矩阵 ans。

② 初始位置与方向

从坐标 (0, 0) 开始，初始方向为右（di = 0）。

③ 填充数字

按当前方向尝试前进到下一个位置 (x, y)。

④ 方向切换逻辑

算法通过索引 di 选择当前方向：

初始方向：di = 0（向右）

转向条件：遇到边界或已填充的位置时

转向操作：di = (di + 1) % 4 → 按 右→下→左→上 循环切换

⑤ 边界检查：

若新位置超出矩阵范围或已被填充，则右转（di = (di + 1) % 4）。更新当前位置 (i, j) 并填充数字。

⑤ 终止条件：

填充完所有 n² 个数字后结束循环。

class Solution:def generateMatrix(self, n: int) -> List[List[int]]:DIRS = [(0, 1), (1, 0), (0, -1), (-1, 0)]  # 右下左上ans = [[0] * n for _ in range(n)]i = j = di = 0for val in range(1, n * n + 1):  # 要填入的数ans[i][j] = valx, y = i + DIRS[di][0], j + DIRS[di][1]  # 下一步的位置# 如果 (x, y) 出界或者已经填入数字if x < 0 or x >= n or y < 0 or y >= n or ans[x][y]:di = (di + 1) % 4  # 右转 90°i += DIRS[di][0]j += DIRS[di][1]  # 走一步return ans

---

Ⅶ、885. 螺旋矩阵 III

在 rows x cols 的网格上，你从单元格 (rStart, cStart) 面朝东面开始。网格的西北角位于第一行第一列，网格的东南角位于最后一行最后一列。

你需要以顺时针按螺旋状行走，访问此网格中的每个位置。每当移动到网格的边界之外时，需要继续在网格之外行走（但稍后可能会返回到网格边界）。

最终，我们到过网格的所有 rows x cols 个空间。

按照访问顺序返回表示网格位置的坐标列表。

示例 1：

输入：rows = 1, cols = 4, rStart = 0, cStart = 0
输出：[[0,0],[0,1],[0,2],[0,3]]

示例 2：

输入：rows = 5, cols = 6, rStart = 1, cStart = 4
输出：[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

提示：

• 1 <= rows, cols <= 100
• 0 <= rStart < rows
• 0 <= cStart < cols

思路与算法

① 方向控制

与螺旋矩阵 I 类似，按右→下→左→上循环切换方向。

② 步长规律

每次转向后，步长递增 1（第一次向右走 1 步，下一次向下走 1 步，再向左走 2 步，向上走 2 步，依此类推）。

③ 边界检查

每走一步，检查坐标是否在矩阵内，若是则记录。

class Solution:def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:DIRS = [(0, 1), (1, 0), (0, -1), (-1, 0)]  # 右、下、左、上res = [[rStart, cStart]]  # 起始点i, j = rStart, cStartsteps = 0  # 当前方向的步数di = 0     # 方向索引while len(res) < rows * cols:# 每次转向后，步数递增1（偶数次转向时增加）if di % 2 == 0:steps += 1# 沿当前方向走steps步for _ in range(steps):i += DIRS[di][0]j += DIRS[di][1]# 检查是否在矩阵内if 0 <= i < rows and 0 <= j < cols:res.append([i, j])# 转向di = (di + 1) % 4return res