当前位置：首页 > news >正文

C++色彩博弈的史诗：红黑树

news 来源：原创 2025/7/17 23:47:57

文章目录

1.红黑树的概念
2.红黑树的结构
3.红黑树的插入
4.红黑树的删除
5.红黑树与AVL树的比较
6.红黑树的验证
希望读者们多多三连支持
小编会继续更新
你们的鼓励就是我前进的动力！

红黑树是一种自平衡二叉查找树，每个节点都带有颜色属性，颜色或为红色或为黑色，可以理解为 AVL 树的进阶版，建议系统学习完 AVL 树再来看本篇博客

传送门：C++漫步结构与平衡的殿堂：AVL树

1.红黑树的概念

在这里插入图片描述

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是 Red 或 Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保最长路径的节点数量不超过最短路径节点数量的两倍（刚好两倍是可以的），因而是接近平衡的

一个合格的红黑树需要满足以下条件：

每个结点不是红色就是黑色
根节点是黑色的
如果一个节点是红色的，则它的两个孩子结点必须是黑色的，任何路径都没有连续的红色节点，也就是说可以有连续的黑色节点，但不可能一颗红黑树全是黑色节点
对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色节点
每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

为什么满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点个数的两倍？

最短路径就是仅由黑色节点构成的路径。因为如果路径中插入红色节点，会使路径变长，而全黑路径不包含额外红色节点，所以是最短的

最长路径是红黑交替出现的路径。即每一个黑色节点后面都跟着一个红色节点（但红色节点后不能再有红色节点）

设最短路径的黑色节点数量为 n ，由于所有路径黑色节点数量相同，最长路径的黑色节点数量也为 n ，那么最长路径由于红黑交替的节点总数最多为 2n 。所以，最长路径的节点个数不会超过最短路径节点个数的两倍

2.红黑树的结构

enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};

在节点的定义中，为什么要将节点的默认颜色给成红色的？

红黑树的性质要求从根节点到每个叶子节点的路径上黑色节点数量相同。将新节点设为红色，在插入过程中，如果其父节点是黑色，那么插入红色节点不会影响任何路径上黑色节点的数量，也就不需要对树进行调整来满足红黑树的性质，从而减少了调整的可能性，提高了插入操作的效率

如果新节点是黑色，那么插入后可能会导致某个路径上的黑色节点数量增加，这会引发更复杂的 “双黑” 问题，即删除或插入操作后出现一个节点需要同时承担两个黑色节点的情况，处理起来相对复杂。而默认新节点为红色，出现的问题主要是红节点冲突，处理相对简单，以下的插入会详细解释原因

3.红黑树的插入

typedef RBTreeNode<K, V> Node;
bool Insert(const pair<K, V>& kv)
{//根节点为空的情况if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//查找插入节点位置Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//链接插入节点与红黑树cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else // u不存在 或 存在且为黑{if (cur == parent->_left){//     g//   p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   p//		cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{Node* uncle = grandfather->_left;// u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){// g//	  p//       cRotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g//	  p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}

对于插入的节点，可能会遇到三种情况：

🚩uncle存在且为红
在这里插入图片描述

我们定义插入节点为 cur，其父节点为 parent，父节点的兄弟节点为 uncle，父节点的父节点为 grandfather

当新插入节点的双亲节点颜色为红色时，就违反了不能有连在一起的红色节点，想要尽可能不破坏红黑树的平衡结构的情况下正常插入，那么通过变色解决是最好的

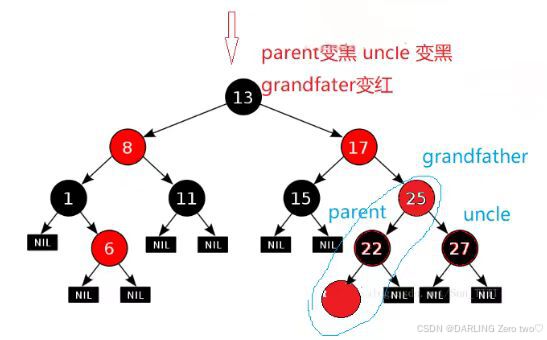
请添加图片描述

不能连续出现红色节点，还要保持每条路径的黑色节点相同，可以将 parent 和 uncle 变黑，grandfather 变红解决

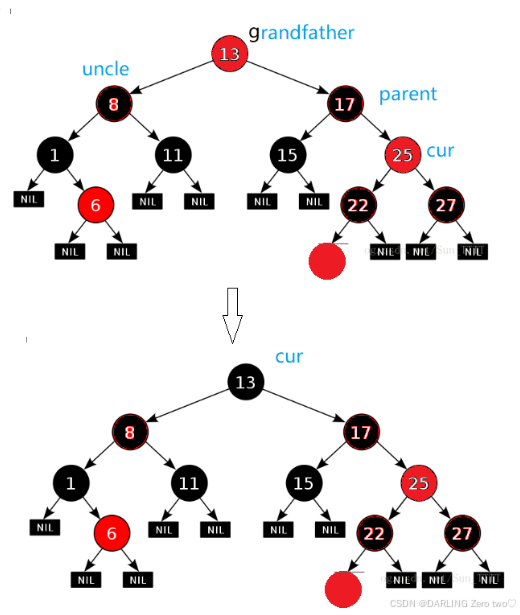
在这里插入图片描述

发现处理完之后，在子树上是保持平衡的，但是 grandfather 又出现了连续红色节点，这是其中一种情况，总共有三种情况：

grandfather 没有父亲，就是根，直接变黑就好了
grandfather 有父亲，父亲是黑色，直接结束
grandfather 有父亲，父亲是红色，重复上述操作

很明显示例就是第三种

🚩uncle不存在

在这里插入图片描述

当 uncle 不存在的时候，发现通过变色已经不能解决问题了，这个时候就要旋转调整结构了，根据 cur 的位置判断进行单旋还是双旋

在这里插入图片描述

然后根据结构性质进行变色即可

🚩uncle存在且为黑
在这里插入图片描述

当 uncle 存在且为黑的时候，情况和 uncle 不存在是一样的

🔥值得注意的是： AVL 树旋转可以根据平衡因子为 2 的相对位置来判断是要单旋还是双旋，红黑树根据 grandfather，parent，cur 的相对位置来判断，也就是要多画图

4.红黑树的删除

红黑树的删除本节不做讲解，有兴趣可参考：《算法导论》或者《STL源码剖析》

传送门：博客园相关讲解

5.红黑树与AVL树的比较

可是红黑树的时间复杂度比AVL树更高啊，为什么反而用的更多？

红黑树	AVL树
最长路径不超过最短路径的2倍	高度差不超过1
10亿个值	10亿个值
2*logN->60	logN->30

可以看到数据，性能处理上大概相差两倍，但是要知道 CPU 的性能是很强大的，每秒能处理十几亿的数据，这点差距根本不足为惧，而且红黑树和 AVL 树是处于同一量级的，但是 AVL 树的插入删除需要大量的旋转，控制严格平衡的代价太大，因此使用红黑树更多

6.红黑树的验证

🚩检查是否有连续红色节点

bool CheckColour(Node* root, int blacknum, int benchmark)
{if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);
}

🚩检查是否平衡

bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr)return true;if (root->_col != BLACK){return false;}// 基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}return CheckColour(root, 0, benchmark);
}int Height()
{return Height(_root);
}int Height(Node* root)
{if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

希望读者们多多三连支持

小编会继续更新

你们的鼓励就是我前进的动力！

请添加图片描述

文章目录

1.红黑树的概念

2.红黑树的结构

3.红黑树的插入

4.红黑树的删除

5.红黑树与AVL树的比较

6.红黑树的验证

希望读者们多多三连支持

小编会继续更新

你们的鼓励就是我前进的动力！

相关文章：