当前位置：首页 > news >正文

常见的排序算法（Java版）简单易懂好上手！！

news 来源：原创 2025/7/22 19:12:42

排序

“排序”顾名思义就是把乱序的变成有序的，就像我们玩斗地主这种牌类游戏时，我们拿到牌都会将牌给排序一下，更好的在对局中方便思考和观察，我们排序算法也亦是如此。

文章目录

排序
一、冒泡排序
二、选择排序
三、插入排序
四、希尔排序
五、归并排序
六、快速排序
总结

一、冒泡排序

冒泡排序的过程就像是我们在烧水时，气泡大的会向上冒，气泡小的则在下面，就是冒泡的一个过程，数字大的就是大气泡，数字小的就是小气泡，例如：
在这里插入图片描述

过程：从第一个数开始和后面一个数进行比较，大了便交换，否则便下一个次比较，如上图所示，用4与5进行比较，4 < 5,则用5与6比较，5 < 6, 则用6与3比较，6 > 3,则交换位置，以此类推6到了最后一个位置则这一个过程则称为第一次冒泡，每一次冒泡就是将未排序的数组中最大数向上推的过程。
代码实例：

public class BubbleSort {
/*//将给定的数组排序public static void sort(Comparable[] arr) {//有几个数就需要比较几次，数比较大的就交换for (int i = 1; i < arr.length; i++) {//前一个数和后一个数比较for (int j = 0; j < arr.length - 1; j++) {if (compare(arr[j],arr[j + 1])) {swap(arr,j,j + 1);}}}}
*///将上面的代码进行改进 => 每次比较后最大的数都将位于数组的最后一位，//                    所以每次排序都可以把原本最后一次比较省略掉public static void sort(Comparable[] arr) {for (int i = arr.length - 1; i > 0; i--) {for (int j = 0; j < i; j++) {if (compare(arr[j], arr[j + 1])) {swap(arr, j, j + 1);}}}}//比较元素大小public static boolean compare(Comparable a, Comparable b) {return a.compareTo(b) > 0;}//交换元素public static void swap(Comparable[] arr, int i, int j) {Comparable temp;temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}

测试一下：
在这里插入图片描述
运行结果

冒泡排序的特性总结：

冒泡排序是一种非常容易理解的排序
时间复杂度：O(N^2)
空间复杂度：O(1)
稳定性：稳定

二、选择排序

选择排序的过程是：在待排序的数组中选择一个最小的元素放在起始位置，直到数组排序完，如下图所示：
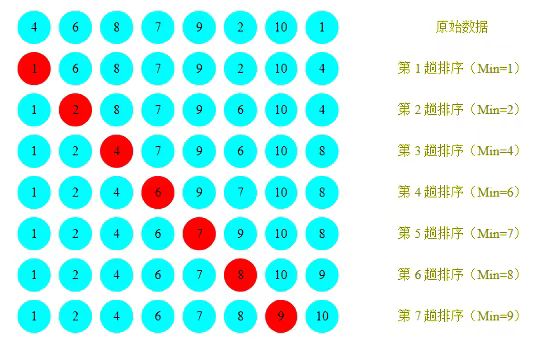
在这里插入图片描述
我们首先假定数组第一个数的下标是最小值的下标索引，然后一次向后比较，遇到较小的数便与其交换下标索引，每次比较完后最小值的下标索引便与待排数组的收尾进行交换，这样便会保证每次交换到的都是待排数组中最小的值，我们可以观察到我们需要进行n-1次排序。
代码实现：

public class SelectSort {public static void sort(Comparable[] arr) {//总共需要比较n - 1次for (int i = 0; i < arr.length - 1; i++) {//定义一个的下标索引，记录最小值的下标int minIndex = i;for (int j = i + 1; j < arr.length; j++) {if (compare(arr[minIndex], arr[j])) {minIndex = j;}}//每次比较完，都要交换i和minIndex下标的值swap(arr, i, minIndex);}}//比较元素大小public static boolean compare(Comparable a, Comparable b) {return a.compareTo(b) > 0;}//交换元素public static void swap(Comparable[] arr, int i, int j) {Comparable temp;temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}

测试一下：
在这里插入图片描述
运行结果：

直接选择排序的特性总结：
1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

三、插入排序

插入排序的过程就像是，我们在打扑克牌或麻将一样，我们要将没有排序的牌进行排序就需要拿起一张牌，然后将其想前比对，比前面的牌小则交换，反之则不变那便是这张牌所属的位置，例如：
在这里插入图片描述
我们将第一位数看做已排好序的，然后后面的剩余的为待排序的，我们进行比较，在合适的位置进行插入，依次类推便得到排好序的结果。
代码实现：

public class InsertSort {public static void sort(Comparable[] arr) {//将数组的首个数字表示为已排序的，后面的未排序的，然后遍历已排序的数组，进行插入for (int i = 1; i < arr.length; i++) {//将数组下标j 和下标j - 1的值进行比较，如果下标j - 1的值大于下标j的值则交换数据，反之则为找到合适的位置，退出循环for (int j = i; j > 0; j--) {if (compare(arr[j - 1], arr[j])) {swap(arr, j -1, j);} else {break;}}}}//比较元素大小public static boolean compare(Comparable a, Comparable b) {return a.compareTo(b) > 0;}//交换元素public static void swap(Comparable[] arr, int i, int j) {Comparable temp;temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}

测试一下：
在这里插入图片描述
运行：

直接插入排序的特性总结：

元素集合越接近有序，直接插入排序算法的时间效率越高
时间复杂度：O(N^2)
空间复杂度：O(1)，它是一种稳定的排序算法
稳定性：稳定

四、希尔排序

希尔排序的过程与插入排序的过程大同小异，又称“缩小增量排序”，是插入排序的升级版，变得更高效一点。具体就是我们先定义一个增量h，然后利用这个增量对数组进行分组，分组完以后进行插入排序，得到的便是接近有序的数组：然后缩小其增量，然后执行上述操作，使增量h缩小至1时，排序后便是有序数组。相对于增量h也有其相关的定义规则和缩小规则：

//确定增长量h的最大值
int h=1;
while(h<N/2){
h=h*2+1;
}
h的减小规则为：
h=h/2

我们给出例图更直观的感受一下：
在这里插入图片描述
归纳一下排序原理：
1.选定一个增长量h，按照增长量h作为数据分组的依据，对数据进行分组；
2.对分好组的每一组数据完成插入排序；
3.减小增长量，最小减为1，重复第二步操作

代码实现：

public class ShellSort {public static void sort(Comparable[] arr) {//数组长度int N = arr.length;//确定增量h的值int h = 1;while (h < N) {h = h * 2 + 1;}//当h<1时，排序结束while (h >= 1){//1.找到待插入的元素for (int i = h; i < N; i++) {//arr[i]就是待插入的元素//然后将arr[i]插入到分好组的序列中arr[i - h],arr[i - 2h]...for (int j = i; j >= h; j-=h) {//将arr[j - h]与arr[j]进行比较，较大则交换，//反之则退出此次循环if (compare(arr[j - h], arr[j])) {swap(arr,j-h, j);} else {break;}}}//2.缩小增量hh /= 2;}}//比较元素大小public static boolean compare(Comparable a, Comparable b) {return a.compareTo(b) > 0;}//交换元素public static void swap(Comparable[] arr, int i, int j) {Comparable temp;temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}

测试一下：

在这里插入图片描述
运行：

希尔排序的特性总结：

希尔排序是对直接插入排序的优化。
当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排序的时间复杂度都不固定：

在这里插入图片描述

五、归并排序

归并排序的过程，是分治法的应用过程，将一组数据尽可能的拆分成两组相同的数据，并对每一组数据在拆分，直到数据的大小为1不可再拆时，我们就向上返回，进行排序，实际也是一种递归的过程，分治法顾名思义就是“分”=>分组，“治”=>共治，两个步骤组成，光光有文字叙述，我觉得会有点难以理解，我们上图看一下，体会这个过程：
在这里插入图片描述

简单概述一下就是：
1.我们对数据进行分组
2.相邻的两组进行合并
在上图我们发现了，其每组的过程都是一样的，只是数据不同，那我们肯定要运用到递归来实现，我们接下来用代码实现在分析：

public class MergeSort {//定义一个辅助数组assistprivate static Comparable[] assist;//将数据进行分组排序public static void sort(Comparable[] arr) {assist = new Comparable[arr.length];//定义左右指针,表示需要进行分组的范围int left = 0;int right = arr.length - 1;//利用sort的重构方法进行分组排序sort(arr, left, right);}public static void sort(Comparable[] arr, int left, int right) {//安全性校验if (right <= left) return;//定义中间指针,进行拆分int mid = left + (right - left) / 2;//递归不断拆分sort(arr, left, mid);sort(arr, mid + 1, right);//进行合并merge(arr,left,mid,right);}//归并public static void merge(Comparable[] arr, int left, int mid, int right) {int index = left;//这个是指向assist数组开始填充的指针int p1 = left;//这个是指向第一组数据的第一个数int p2 = mid + 1;//指向第二组数据的第一个数//两组数据依次进行比较,较小的数填充到assist数组中,指针向后移,//循环结束条件就是有一组数据已经遍历完了,退出while (p1 <= mid && p2 <= right) {if (compare(arr[p1], arr[p2])) {//如果arr[p1] 大于 arr[p2],则填充arr[p2]assist[index++] = arr[p2++];}else {//反之则填充arr[p1]assist[index++] = arr[p1++];}}//跳出循环后,表示有一组数据已经遍历完了,那我们需要将剩下一组没有遍历完的数据直接顺序填充即可,因为同一组数据本身就是一排好序的//但是我们并不知道的是那组数据先结束,所以都需要进行判断while (p1 <= mid) {assist[index++] = arr[p1++];}while (p2 <= right) {assist[index++] = arr[p2++];}//我们只需将我们排好序的辅助数组assist复制到原数组即可for (int i = 0; i <= right; i++) {arr[i] = assist[i];}}//比较元素大小public static boolean compare(Comparable a, Comparable b) {return a.compareTo(b) > 0;}//交换元素public static void swap(Comparable[] arr, int i, int j) {Comparable temp;temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}

整个的代码量还是相对较多的,但具体都挺好理解的,我们自己画一画整个过程,明白了其具体流程,我们在敲代码的时候也是手到擒来哈哈哈,其中我们要注意的是一些边界条件,如果边界条件没有弄清楚,很容易就迷了,多多练习,理解每一次都会有不同的收获.
其中我们利用辅助数组对其填充,就是比较两组数据大小,然后填到一个空数组中的一个过程,如图:
在这里插入图片描述

我们进行测试一下:
在这里插入图片描述

归并排序总结:

归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
时间复杂度：O(N*logN)
空间复杂度：O(N)
稳定性：稳定

六、快速排序

快速排序是对冒泡排序的一种改进。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
排序原理：
1.首先设定一个分界值，通过该分界值将数组分成左右两部分；
2.将大于或等于分界值的数据放到到数组右边，小于分界值的数据放到数组的左边.此时左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值；
3.然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
4.重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后，整个数组的排序也就完成了。
具体的我们还是得通过图例才能更好的表现出来:

![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/4306dc039d864efe94ba53309e9115e8.png代码实现:

代码实现:

public class QuickSort {public static void sort(Comparable[] arr) {int p1 = 0;//首个元素的下标int p2 = arr.length - 1;//最后一个元素的下标//将数据的p1~p2元素进行排序sort(arr, p1, p2);}public static void sort(Comparable[] arr, int p1, int p2) {//安全性检查if (p2 <= p1) return;//对数据进行切分int partition = partition(arr, p1, p2);//partition的下标的值是基准值,我们将其左右两部分分开排序//将p1~partition - 1的元素进行排序sort(arr,p1,partition - 1);//将partition + 1~p2之间的元素进行排序sort(arr,partition + 1, p2);}public static int partition(Comparable[] arr, int p1, int p2) {//我们通常定义首个元素为基准值Comparable key = arr[p1];//定义左右指针,分别指向首元素和尾元素int left = p1;int right = p2 + 1;//进行切分//从右往左找比基准值小的数//从左往右找比基准值大的数while (true) {// 1.首先从右往左扫描while (compare(arr[--right], key)) {//如果扫描完发现都没有比基准值小的数,则退出循环if (right == p1) break;}// 2.从左往右扫描while (compare(key, arr[++left])) {//如果扫描完发现都没有比基准值大的数,则退出循环if (left == p2) break;}//当左指针和右指针相遇时,则表示扫描完毕,即可退出循环if (left >= right) {break;} else {//当左右指针还没有相遇时,找到相应的数了,交换位置swap(arr, left, right);}}//每趟循环完成,交换基准值和左右指针相遇位置的值即可swap(arr, p1, right);//左右指针相遇的地方就是切分的位置,所以这里返回left或者right都可以return right;}//比较元素大小public static boolean compare(Comparable a, Comparable b) {return a.compareTo(b) > 0;}//交换元素public static void swap(Comparable[] arr, int i, int j) {Comparable temp;temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}

测试一下:
在这里插入图片描述

快速排序总结:

快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
时间复杂度：O(N*logN)
空间复杂度：O(logN)
稳定性：不稳定

总结

这里总结了我们常见算法的一些原理,是自己学习过程中的一些总结,希望对大家也有所帮助.

排序