当前位置：首页 > news >正文

STM32实现九轴IMU的卡尔曼滤波

news 来源：原创 2025/8/1 22:16:56

在嵌入式系统中，精确的姿态估计对于无人机、机器人和虚拟现实等应用至关重要。九轴惯性测量单元（IMU）通过三轴加速度计、陀螺仪和磁力计提供全面的运动数据。然而，这些传感器数据常伴随噪声和漂移，单独使用无法满足高精度需求。卡尔曼滤波作为一种强大的传感器融合算法，能够有效结合多传感器数据，估计系统状态。

九轴IMU通常由以下三部分组成：

三轴加速度计：测量线性加速度，可用于确定重力方向和线性运动
三轴陀螺仪：测量角速度，用于检测旋转运动
三轴磁力计：测量地磁场，提供绝对方向参考

这些传感器的互补特性使得传感器融合成为必要。融合算法通过结合各传感器数据，克服单一传感器的局限性，提供更准确的姿态估计。

由于各传感器存在固有缺陷（如陀螺仪漂移、加速度计噪声、磁力计干扰），单独使用无法提供可靠的姿态估计。传感器融合通过数学模型整合多传感器数据，生成更精确的估计结果。常用的融合算法包括互补滤波和卡尔曼滤波，其中卡尔曼滤波因其理论最优性广泛应用于姿态估计。

卡尔曼滤波是一种递归算法，用于从噪声测量中估计动态系统的状态。它假设系统是线性的，噪声为高斯分布。卡尔曼滤波包括两个主要步骤：

预测步骤：根据系统模型预测下一时刻的状态和协方差。
更新步骤：利用新测量值修正预测状态，计算卡尔曼增益以平衡预测和测量。

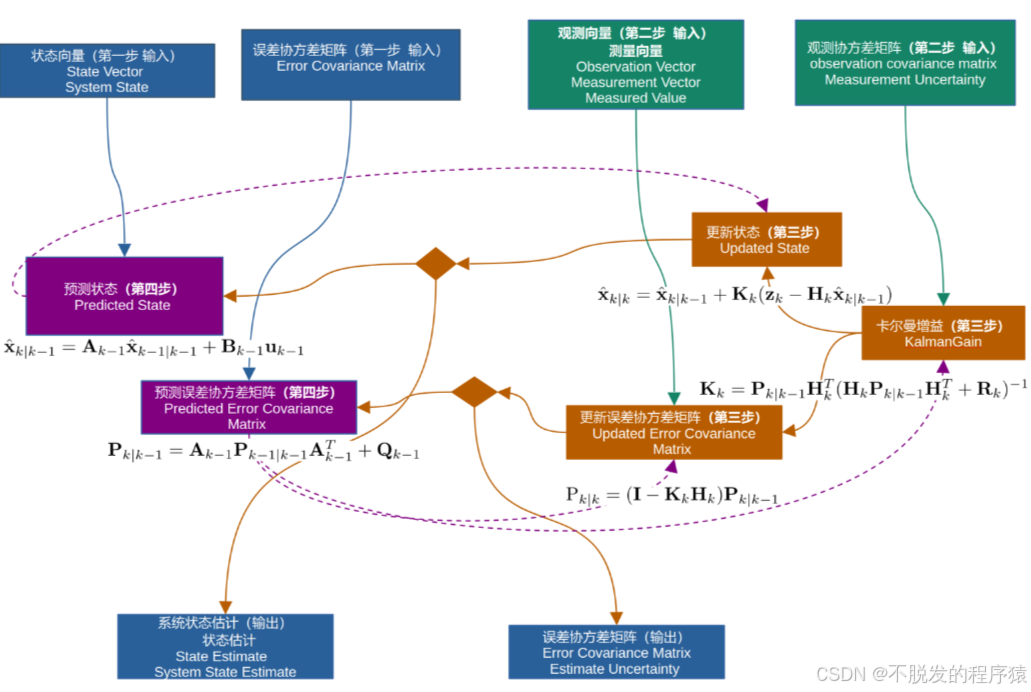
对于卡尔曼滤波的原理，我们不再细究，网上有很多资料，本篇文章主要讲解嵌入式工程师如何使用代码实现卡尔曼滤波。

在STM32微控制器上实现九轴IMU的卡尔曼滤波需要选择一款支持浮点运算单元（FPU）的STM32微控制器（如STM32F4系列），以高效处理矩阵运算。将九轴IMU（如MPU9250）通过I2C或SPI接口连接到STM32开发板。确保电源稳定，通信线路正确连接。

以下是九轴IMU卡尔曼滤波的核心实现：

// 状态向量：[q0, q1, q2, q3, bgx, bgy, bgz]
float state[7];// 状态协方差矩阵 P (7x7)
float P[49];// 过程噪声协方差矩阵 Q (7x7)
float Q[49];// 观测噪声协方差矩阵 R (6x6)：3个加速度计和3个磁力计
float R[36];// 状态转换矩阵 F (7x7)
float F[49];// 观测矩阵 H (6x7)
float H[42];// 卡尔曼增益 K (7x6)
float K[42];// 预测状态
float state_pred[7];// 预测协方差
float P_pred[49];// 残差
float y[6];// S = H*P*H^T + R
float S[36];// 初始状态
void init_state(float initial_q[4], float initial_bg[3]) {// 初始化状态向量memcpy(state, initial_q, 4*sizeof(float));memcpy(state+4, initial_bg, 3*sizeof(float));// 初始化协方差矩阵 Pmemset(P, 0, 49*sizeof(float));P[0] = 0.01f; P[7] = 0.01f; P[14] = 0.01f; P[21] = 0.01f; // q的方差P[28] = 0.01f; P[35] = 0.01f; P[42] = 0.01f; // bg的方差// 初始化过程噪声协方差 Qmemset(Q, 0, 49*sizeof(float));Q[0] = 0.001f; Q[7] = 0.001f; Q[14] = 0.001f; Q[21] = 0.001f; // q的噪声Q[28] = 0.0001f; Q[35] = 0.0001f; Q[42] = 0.0001f; // bg的噪声// 初始化观测噪声协方差 Rmemset(R, 0, 36*sizeof(float));R[0] = 0.1f; R[7] = 0.1f; R[14] = 0.1f; // 加速度计噪声R[21] = 0.1f; R[28] = 0.1f; R[35] = 0.1f; // 磁力计噪声
}// 预测步骤
void predict(float gyro[3], float dt) {// 计算角速度四元数float omega[4] = {0, gyro[0], gyro[1], gyro[2]};float theta = sqrt(omega[1]*omega[1] + omega[2]*omega[2] + omega[3]*omega[3]) * dt;float axis[3];if (theta > 1e-6) {axis[0] = omega[1]/theta;axis[1] = omega[2]/theta;axis[2] = omega[3]/theta;} else {axis[0] = 0;axis[1] = 0;axis[2] = 0;}float dq[4] = {cos(theta/2), axis[0]*sin(theta/2), axis[1]*sin(theta/2), axis[2]*sin(theta/2)};// 预测四元数float q[4];quaternion_multiply(state, dq, q);quaternion_normalize(q);memcpy(state_pred, q, 4*sizeof(float));// 陀螺仪偏置保持不变memcpy(state_pred+4, state+4, 3*sizeof(float));// 计算状态转换矩阵 F// (这里简化为恒等矩阵，实际应用中需要正确计算)memset(F, 0, 49*sizeof(float));for(int i=0; i<7; i++) F[i*8] = 1.0f;// P_pred = F*P*F^T + G*Q*G^T// (这里简化为P_pred = P + Q)for(int i=0; i<49; i++) P_pred[i] = P[i] + Q[i];// 更新状态和协方差memcpy(state, state_pred, 7*sizeof(float));memcpy(P, P_pred, 49*sizeof(float));
}// 更新步骤
void update(float acc[3], float mag[3], float ref_mag[3]) {// 计算期望的加速度计测量值float q_inv[4];quaternion_conjugate(state, q_inv);float expected_acc[4] = {0, 0, 0, -1};quaternion_multiply(state, expected_acc, expected_acc);quaternion_multiply(expected_acc, q_inv, expected_acc);expected_acc[1] /= expected_acc[0];expected_acc[2] /= expected_acc[0];expected_acc[3] /= expected_acc[0];// 计算期望的磁力计测量值float expected_mag[4];quaternion_multiply(state, ref_mag, expected_mag);quaternion_multiply(expected_mag, q_inv, expected_mag);expected_mag[1] /= expected_mag[0];expected_mag[2] /= expected_mag[0];expected_mag[3] /= expected_mag[0];// 组合观测向量float z[6] = {acc[0], acc[1], acc[2],mag[0], mag[1], mag[2]};float h[6] = {expected_acc[1], expected_acc[2], expected_acc[3],expected_mag[1], expected_mag[2], expected_mag[3]};// 计算残差for(int i=0; i<6; i++) y[i] = z[i] - h[i];// 计算观测矩阵 H// (这里简化为恒等矩阵，实际应用中需要正确计算)memset(H, 0, 42*sizeof(float));for(int i=0; i<6; i++) H[i*8 + i] = 1.0f;// 计算 S = H*P*H^T + R// (这里简化为 S = H*P*H^T + R)memset(S, 0, 36*sizeof(float));for(int i=0; i<6; i++) {for(int j=0; j<7; j++) {if (H[i*7 + j] == 0) continue;for(int k=0; k<6; k++) {if (H[k*7 + j] == 0) continue;S[i*6 + k] += H[i*7 + j] * P[j*7 + k] * H[k*7 + j];}}}for(int i=0; i<36; i++) S[i] += R[i];// 计算卡尔曼增益 K = P*H^T*S^{-1}// (这里简化为 K = P*H^T / (H*P*H^T + R))memset(K, 0, 42*sizeof(float));for(int i=0; i<7; i++) {for(int j=0; j<6; j++) {float sum = 0;for(int k=0; k<7; k++) {sum += P[i*7 + k] * H[j*7 + k];}K[i*6 + j] = sum / S[j*6 + j];}}// 更新状态for(int i=0; i<7; i++) {float sum = 0;for(int j=0; j<6; j++) {sum += K[i*6 + j] * y[j];}state[i] += sum;}// 更新协方差memset(P, 0, 49*sizeof(float));for(int i=0; i<7; i++) {for(int j=0; j<7; j++) {float sum = 0;for(int k=0; k<6; k++) {sum += K[i*6 + k] * H[k*7 + j];}P[i*7 + j] = (1 - sum) * P_pred[i*7 + j];}}
}

以下是完整的STM32实现框架：

#include "stm32f10x.h"// 定义MPU9250和HMC5883L的I2C地址
#define MPU9250_ADDR 0x68
#define HMC5883L_ADDR 0x1E// MPU9250寄存器定义
#define PWR_MGMT_1 0x6B
#define SMPLRT_DIV 0x19
#define CONFIG 0x1A
#define GYRO_CONFIG 0x1B
#define ACCEL_CONFIG 0x1C
#define INT_ENABLE 0x38
#define PWR_MGMT_2 0x3B// HMC5883L寄存器定义
#define HMC5883L_CTRL_REG_A 0x0A
#define HMC5883L_CTRL_REG_B 0x0B// 状态向量：[q0, q1, q2, q3, bgx, bgy, bgz]
float state[7];// 状态协方差矩阵 P (7x7)
float P[49];// ... 其他变量声明// I2C写操作
void i2c_write(uint8_t addr, uint8_t reg, uint8_t value) {// 实现I2C写操作
}// I2C读操作
uint8_t i2c_read(uint8_t addr, uint8_t reg) {// 实现I2C读操作
}// 四元数乘法
void quaternion_multiply(float *q1, float *q2, float *result) {// 实现四元数乘法
}// 四元数归一化
void quaternion_normalize(float *q) {// 实现四元数归一化
}// 四元数共轭
void quaternion_conjugate(float *q, float *result) {// 实现四元数共轭
}// MPU9250初始化
void mpu9250_init(void) {// 实现MPU9250初始化
}// 从MPU9250读取加速度计数据
void read_accel(float *accel) {// 从MPU9250读取加速度计数据
}// 从MPU9250读取陀螺仪数据
void read_gyro(float *gyro) {// 从MPU9250读取陀螺仪数据
}// 从HMC5883L读取磁力计数据
void read_magnet(float *magnet) {// 从HMC5883L读取磁力计数据
}// 初始化卡尔曼滤波器
void init_kalman(float initial_q[4], float initial_bg[3]) {// 初始化卡尔曼滤波器
}// 卡尔曼滤波预测步骤
void kalman_predict(float gyro[3], float dt) {// 实现卡尔曼滤波预测步骤
}// 卡尔曼滤波更新步骤
void kalman_update(float accel[3], float magnet[3], float ref_magnet[3]) {// 实现卡尔曼滤波更新步骤
}int main(void) {// 初始化STM32外设// ...// 初始化MPU9250mpu9250_init();// 初始化卡尔曼滤波器float initial_q[4] = {1, 0, 0, 0}; // 初始姿态为0角度float initial_bg[3] = {0, 0, 0}; // 初始陀螺仪偏置为0init_kalman(initial_q, initial_bg);// 参考地磁场值(根据实际位置确定)float ref_magnet[3] = {0, 0, -1}; // 南极指向地心float gyro[3], accel[3], magnet[3];while(1) {// 读取传感器数据read_gyro(gyro);read_accel(accel);read_magnet(magnet);// 预测步骤float dt = 0.01; // 10ms采样周期kalman_predict(gyro, dt);// 更新步骤kalman_update(accel, magnet, ref_magnet);// 处理滤波结果// ...// 延时Delay_Ms(10);}
}

如果不想自己手写代码，可以使用STMicroelectronics的MotionFX库。

它是X-CUBE-MEMS1软件扩展的一部分，内置优化的卡尔曼滤波算法，支持6轴和9轴IMU融合。该库针对STM32微控制器优化，适合快速开发。

MotionFX库在不同STM32平台上的性能效果如下：

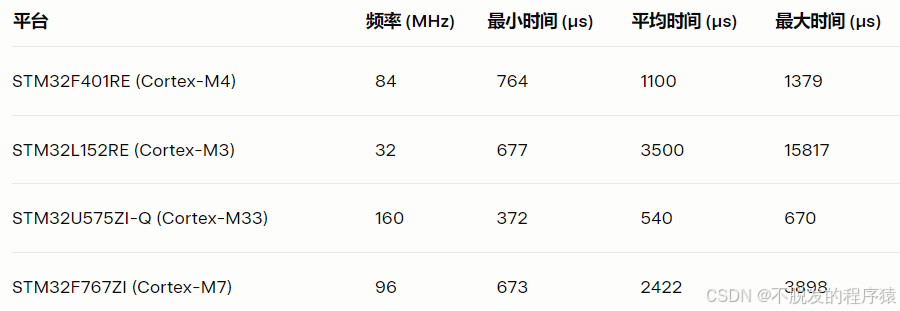
在STM32上实现九轴IMU的卡尔曼滤波是嵌入式系统中实现高精度姿态估计的有效方法。通过理解IMU的工作原理、卡尔曼滤波的理论以及系统建模，开发者可以从头实现EKF算法。或者，利用ST的MotionFX库可以显著简化开发流程，同时保持高性能。

相关文章：