Dp通用套路(闫式)
闫式dp分析法:
从集合角度来分析DP问题。
核心思想:
DP是一种求有限集中的最值或者个数问题
由于集合中元素的数量都是指数级别的,直接用定义去求,把每种方案都用dfs暴力枚举一遍,时间复杂度很高,此时用DP问题去优化。
DP 优化两个阶段(核心思想)

动态规划解题步骤
步骤一:确定集合以及集合的属性
将问题看成一个集合,按照上述集合划分依据,分成若干不同子集。
按照属性定义状态,例如用 f[i] 表示考虑前 i 个元素时的某种最优解或状态。
步骤二: 状态计算
找出状态之间的关系,即状态转移方程。这个方程描述了如何从已知子集的解构建出整个集合的解。
步骤三:确定初始值
确定基本情况或边界条件。这些是状态转移方程中无法通过递推得到,需要直接给出的值。有时候可以直接将f数组定义为全局数组,则数组的元素会被默认初始化为0。
例如f[0] = 0 ,表示容量为0时的最大价值为0。
步骤四:输出结果
根据问题的要求,输出最终结果。在很多情况下,最终结果存储在 f[n] 中,其中 n 是问题的规模。
eg:01背包问题
分析:
从2的n次方个方案中,找到总价值最大的方案,即有限集合中的最值问题,用闫式DP分析法来做。

分别求出左边的最大值,右边集合的最大值,两边取max,就是f(i,j) 的值

左边=f(i-1,j)
右边:每个方案都包含i,不变,要想值最大,需要前面变化的(1~i-1)部分最大
朴素代码

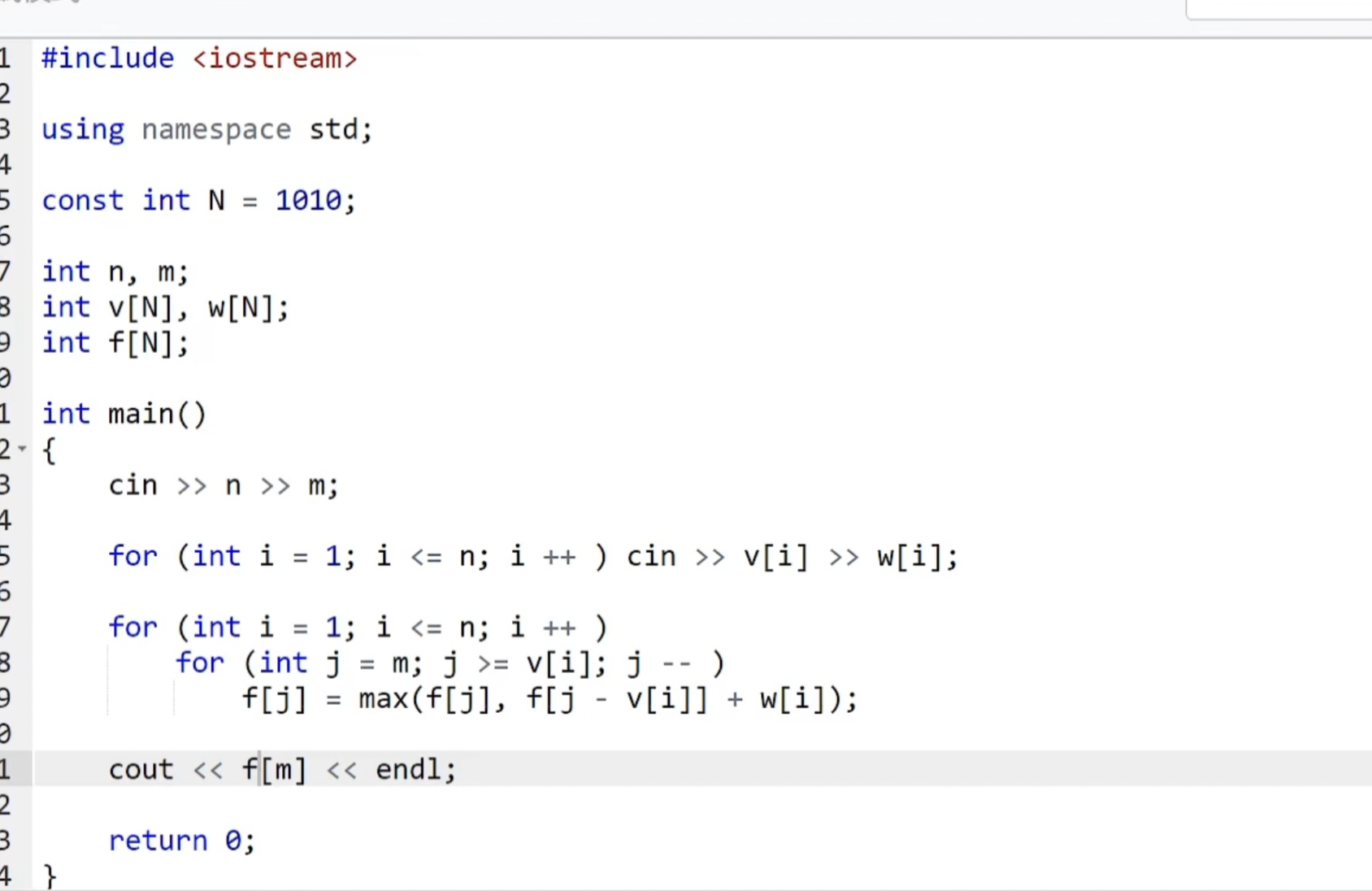
优化空间后的代码
DP问题所有的优化都是对代码做等价变形
等价变形过程如下

由上图分析可得,与原方程不等价。为了使之等价,可以将内层倒序循环(由大到小循环),这样fj会比这件f(j-vi)先更新,那么此时用到的j-vi一定是上一层的,即第i-1层。

继续优化,删掉恒等式f[j]=f[j]等得到优化结果
注意:
必须保证代码优化后是等价的
内层循环:遍历每个可能的容量是为了计算在不同容量限制下的最大价值,确保我们考虑了所有可能的容量。因为在考虑第i个物品是否放入背包的时候,我们需要用当前背包的容量减去第i个物品的体积,而第i个物品的体积是任意的,因此我们需要考虑第i个物品在所有可能的容量限制下的最大价值,从而能够通过比较放入和不放入当前物品时的价值计算出在每个容量下的最大价值。
eg2:完全背包
闫式DP分析问题

朴素代码

优化空间后的代码
按照01背包问题的方法做等价变形过程如下

如图,恰好等价
继续优化,删掉恒等式f[j]=f[j],将判断条件放到内层循环初始化里,因为不满足这个条件的部分会被直接跳过。
得到代码

两个问题状态转移方程如下

eg3:石子合并(区间DP问题)
分析

第一次可以选择合并的堆数是n-1,因为一共有n排,选择的相邻堆一共n-1种选法。第二次合并的时候,就剩下n-1堆,相邻两堆的个数只剩下了n-2,所以第二次合并的时候只剩下了n-2种选法,以此类推,所有不同的合并顺序一共有(n-1)!种。
满足有限集,方案很多,可以考虑DP
由分析可知,最后合并的时候一定是把左边的某一段和右边的某一段合并,因此可以分界点作为划分的依据,具体来说可以以左半边连续一段的最后一堆,如上图,最后一堆可以在第i个位置,以此类推。但至少要有两堆,所以左边这一堆最大到j-1,因此可以分成上面的j-i类。
现在只要把每一类求出来取一个min,即每个子集的min,再从这些min中取出一个最小值,就是整个集合的最小值。
最终的f[i][j]枚举k,从i到j-1 ,在里面取一个min即可。
代码

区间dp问题:先枚举区间长度,再枚举区间左端点,若区间长度为1,不用合并,所以从长度2开始枚举。
因为要在区间长度一定的情况下,在同一[i,j]区间枚举所有k的可能取值中最f[i][j]的最小值,可以先让f[i][j]等于一个正无穷,然后再枚举k
f[i][j]含义:所有将[i,j]区间合并成一堆的方案的集合中的最小值。
总体思想:把这一排石子看成一个集合,然后枚举所有可能的区间当成一个子集。在每个区间中把石子分成左右两堆,K为左右两堆的分界点,每一次枚举k,都要更新当前区间合并石子的最小值。最终根据f数组的含义,f[1][n]即为答案。
eg3:最长公共子序列
子串要求连续,子序列只要求相对顺序。
一个长度为n的序列,据每个数是在或不在这个子序列两种情况,所以一共有2的n次方个不同的子序列。暴力枚举一定会超时,所以用dp来做。
分析

按照最后一个不同点划分:第一个字符串的最后一个字符a[i]是否包含在这个子序列里,第二个字符串的最后一个字b[j]是否包含在这个字序列里来划分。a[i]和b[j]是否包含各有两种选择,所以一共是四种选择。用0表示不包含,1表示包含,前面的代表a[i],后面的代表b[j],四种情况如上图
对于11这种情况,只有a[i]=b[j]时才存在
对于01这种情况,f(i-1, j) 不一定会存在 bj,但已经考虑了含概 bj 可能中的最大值,虽然不含 ai 和 bj 已经在 00 中考虑了,这里就是重复,求最大最小值,重复考虑是没问题的,但是求和的时候不能重复考虑。
同理,对于10这种情况,重复考虑也是没问题。
f[i][j]含义:所有序列a[1~i]与序列b[1~j]的公共子序列的集合中,最长公共子序列的长度。
因此,f[n][m]即为最终答案。
代码

最后
我们要相信科学,不要相信玄学。
如果上述解释有不对的地方,欢迎大家指正
相关文章:
)
Dp通用套路(闫式)
闫式dp分析法: 从集合角度来分析DP问题。 核心思想: DP是一种求有限集中的最值或者个数问题 由于集合中元素的数量都是指数级别的,直接用定义去求,把每种方案都用dfs暴力枚举一遍,时间复杂度很高,此时用…...

如何删除豆包本地大模型
由于无法选择大模型的安装位置,因此会占用C盘大量空间,然后又找到不卸载的地方,经排查豆包大模型安装位为:C:\Users\[当前电脑用户]\AppData\Local\Doubao\User Data,只能进行手动卸载。...

在ISOLAR A/B 工具使用UDS 0x14服务清除单个DTC故障的配置
在ISOLAR A/B 工具使用UDS 0x14服务清除单个DTC故障的配置如下图所示 将DemClearDTCLimitation参数改成DEM_ALL_SUPPORTED_DTCS 此时0x14 服务就可以支持单个DTC的故障清除, 如果配置成 DEM_ONLY_CLEAR_ALL_DTCS 则只能够用0x14服务清楚所有DTC。...

Linux59 SSH配置前瞻 JumpServer双网卡ping通
为什么Ping这个IP地址Ping得通 本地址 [rootlocalhost network-scripts]# cat ifcfg-ens33 iTYPEEthernet BOOTPROTOnone DEFROUTEyes DEVICEens33 ONBOOTno IPADDR192.168.235.4 NETMASK255.255.255.0 GATEWAY192.168.235.2 DNS1114.114.114.114 [rootlocalhost network-scrip…...

TensorFlow中数据集的创建
目录 前言示例示例1示例2示例3示例4 前言 TensorFlow 的 tf.data.Dataset API 提供了一种灵活且高效的方式来加载和预处理数据。它可以轻松处理大规模数据集,并支持多种数据源格式。 所有数据集相关的内容都在tf.data中,from_tensor_slices:…...

OpenHarmony SystemUI开发——实现全局导航栏和状态栏关闭
在实际生产中,进场遇到需要关闭导航栏和状态栏的需求,现分享解决办法: 开发环境 OpenHarmony 5.0.0r 代码分析 思路: launcher本身可以关闭 导航栏(实际是 公共事件,发送消息给systemUI来实控制&#x…...

机器视觉的平板电脑屏幕组件覆膜应用
在现代智能制造业中,平板电脑屏幕组件覆膜工序是确保产品外观和功能完整性的重要环节。随着技术的进步,传统的覆膜方式已经无法满足高速度、高精度的生产需求。而MasterAlign视觉系统的出现,将传统覆膜工艺转变为智能化、自动化的生产流程。在…...
)
Windows 10 无法启动或黑屏的修复指南(适用于更新失败或磁盘故障)
Windows 10 无法启动或黑屏的修复指南(适用于更新失败或磁盘故障) 当 Windows 10 突然无法启动(黑屏、无限重启、更新失败后断电等情况),很可能是由于启动引导程序损坏或系统映像异常(如系统磁盘出现坏道&…...

AI星智协脑:智能驱动的高效协作管理平台全解读
前言 想象一下:早上刚开电脑,十几条未读消息如机关枪般扫射而来,各路任务像陨石雨一样砸向你,会议排得比热播剧还密集,文档版本堪比宫斗剧剧情反转,同事围着你转圈追KPI,活脱脱一场《职场大逃杀…...

WebSocket:实时通信的新时代
在现代Web应用中,实时通信变得越来越重要。传统的HTTP协议虽然能够满足基本的请求-响应模式,但在需要频繁更新数据的场景下,其效率和性能显得捉襟见肘。WebSocket协议应运而生,它提供了一种在单个TCP连接上进行全双工通信的机制&a…...

NetSuite Saved Search如何在Criteria中利用Expressions处理不同Transaction之间的关系?
最近有几个Saved Search都用到了Criteria中的Use Expressions的参数,具体的场景是我们想要对不同的Transaction Type做出不同条件的限定,这里有两个不同的举例。 1.除了ER类型头和行的内容要根据实际取,其余所有Transaction类型都取头信息&a…...

2025年 全新 AI 编程工具 Cursor 安装使用教程
一、Cursor 软件下载 首选,登录Cursor官网,进行软件下载,官网下载地址如下: Cursor AI IDE 下载 二、Cursor软件安装配置 此处以Windows10系统安装为例,下载完成之后,右键安装包,以管理员身份…...

跨平台编码规范文档
1. 引言 1.1 目的与范围 本编码规范旨在为软件开发团队提供统一的代码编写标准,以提高代码质量、可维护性和团队协作效率。适用于使用C#、Java、安卓和Web前端(HTML/CSS/JavaScript/TypeScript)的项目开发,不针对特定语言特性&a…...

Spring创建的线程池
在自动审核的方法上加上Async注解(标明要异步调用) Async//异步方法调用public void audit(WmNews wmNews) {//这个方法处理时间很长,单体异步思想,线程池}在自媒体引导类中使用EnableAsync注解开启异步调用 SpringBootApplicati…...

【深度学习新浪潮】苹果在显示算法技术上的研发进展调研
苹果的显示算法技术研发呈现三大趋势:AI深度整合(如HDR增强、动态校准)、多模态环境感知(光、温湿度、生物特征)、软硬件协同优化(芯片、传感器、算法深度耦合)。 一、动态刷新率与功耗管理 1. ProMotion技术的算法升级 技术修正: 像素级功耗管理:iPhone 13系列的Pr…...
)
图像画质算法记录(前言)
一、背景介绍 本篇主要是对图像画质增强相关,进行简单整理和记录。 二、整体流程 整体效果主要受到两部分影响: 1、前端isp处理。 2、后端画质增强。 三、isp常规流程 可以参考:刘斯宁:Understanding ISP Pipeline 四、后端画质…...
)
uniapp-商城-47-后台 分类数据的生成(通过数据)
在第46章节中,我们为后台数据创建了分类的数据表结构schema,使得可以通过后台添加数据并保存,同时使用云函数进行数据库数据的读取。文章详细介绍了如何通过前端代码实现分类管理功能,包括获取数据、添加、更新和删除分类。主要代…...

阿里云服务器数据库故障排查指南?
阿里云服务器数据库故障排查指南? 以下是针对阿里云服务器(如ECS自建数据库或阿里云RDS等托管数据库)的故障排查指南,涵盖常见问题的定位与解决方案: 一、数据库连接失败 检查网络连通性 ECS自建数据库 确认安全组规则放行数据库…...

服务器不备案有影响吗
在当今数字化的时代,服务器成为了众多企业和个人开展业务、展示自我的重要工具。然而,有一个问题常常被忽视,那就是服务器不备案到底有没有影响? 答案是肯定的!服务器不备案,影响可不小。据相关数据显示&a…...
)
LVGL9保姆级教程(源码获取)
文章目录 🌟 LVGL 9 源码获取全流程指南📥 获取 LVGL 9 源码✅ 官方 GitHub 仓库下载📌 下载步骤: 🛠️ 获取 LVGL Code::Blocks 工程源码下载步骤有两种方式:🚀 方法一:通过 README…...

【react组件】矩形框选小组件,鼠标左键选中 div,键盘 ESC 清空
在线预览 GitHub demo import React, { useState } from react; import Chooser from rc-chooser;const containerStyle: React.CSSProperties {display: flex,alignItems: center,justifyContent: center,flexWrap: wrap, };const boxStyle: React.CSSProperties {width:…...

数据结构5.0
大家好,今天是队列的知识哦~ 目录 一、概念 1.0单链表 2.0双链表 3.0数组 二、队列的方法 1.0 offer方法 2.0 poll方法 3.0 peek方法 4.0 isEmpty方法 三、队列的题目 1.0 用队列实现栈 2.0 用栈实现队列 3.0 设计循环队列 一、概念 数组 、单链表和双…...

Python字典:数据操作的核心容器
在Python编程生态中,字典(dict)是最常用且功能强大的内置数据结构之一。它以键值对(Key-Value Pair)的形式存储数据,为快速查找、灵活映射关系提供了天然支持。无论是数据清洗、算法实现还是Web开发&#x…...

Midjourney-V7:支持参考图片头像或背景生成新保真图
Midjourney-V7重磅升级Omni Reference:全能图像参考神器!再也不用担心生成图片货不对版了! 就在上周,Midjourney发版它最新的V7版本:Omini Reference,提供了全方位图像参考功能,它可以参考你提…...

【MySQL数据库】--SQLyog创建数据库+python连接
目录 1.连接本地数据库 2.创建数据库和表 3.使用 python读取数据 1.连接本地数据库 进入SQLyog 2.创建数据库和表 创建数据库gyp_test: CREATE DATABASE gyp_test CHARACTER SET utf8mb4 COLLATE utf8mb4_general_ci; 创建表student_grade: CREATE TABLE …...

深入解析:思维链模型在大语言模型中的应用与实践
在人工智能领域,大语言模型的发展正以前所未有的速度改变着我们的生活和工作方式。从早期的文本生成到如今的复杂推理,模型的能力不断进化。而其中,思维链(Chain-of-Thought, CoT)技术的出现,更是为大模型的…...
)
服务器多客户端连接核心要点(1)
刷题 服务器多客户端连接核心要点 多进程服务器 实现原理 fork子进程:每次accept新客户端后,调用fork创建子进程。独立处理:子进程负责与客户端通信(如read/write),父进程继续监听新连接。 特点 隔离性…...

SIGIR 2025端到端生成式推荐ETEGRec
文章目录 1. 背景2. 方法2.1 框架图2.2 问题定义2.3 Item Tokenizer2.4 Generative Recommender2.5 ⭐️Sequence-Item Alignment2.6 ⭐️Preference-Semantic Alignment2.7 交替优化 3. 总结 现阶段 GRM 大多是两阶段的模型,第一阶段进行内容理解-行为语义对齐&…...

rust 中的 EBNF 介绍
在 rust 参考手册中,有大量类似: 句法 MacroInvocation :SimplePath ! DelimTokenTreeDelimTokenTree :( TokenTree* )| [ TokenTree* ]| { TokenTree* }TokenTree :Token排除 定界符(delimiters) | DelimTokenTreeMacroInvocationSemi :SimplePath ! (…...

解决 Redis 缓存与数据库一致性问题的技术指南
Redis 缓存与数据库一致性是分布式系统中常见的挑战,尤其在高并发场景下(如电商、用户管理、对账系统)。Redis 作为高性能缓存,常用于加速数据访问,但其与数据库(如 MySQL)之间的数据同步可能因…...

LlamaIndex 第六篇 SimpleDirectoryReader
SimpleDirectoryReader 是将本地文件数据加载到 LlamaIndex 的最简单方式。虽然在实际生产场景中,您更可能需要使用 LlamaHub 提供的多种数据读取器(Reader),但 SimpleDirectoryReader 无疑是快速入门的理想选择。 支持的文件类型…...

window 显示驱动开发-配置内存段类型
视频内存管理器(VidMm)和显示硬件仅支持某些类型的内存段。 因此,内核模式显示微型端口驱动程序(KMD)只能配置这些类型的段。 KMD 可以配置内存空间段和光圈空间段,其中不同: 内存空间段由保存…...

【人工智能学习之动作识别TSM训练与部署】
【人工智能学习之动作识别TSM训练与部署】 基于MMAction2动作识别项目的开发一、MMAction2的安装二、数据集制作三、模型训练1. 配置文件准备2. 关键参数修改3. 启动训练4. 启动成功 ONNX模型部署方案一、环境准备二、执行转换命令 基于MMAction2动作识别项目的开发 一、MMAct…...

PostgreSQL冻结过程
1.冻结过程 冻结过程有两种模式,依特定条件而择其一执行。为方便起见,将这两种模式分别称为惰性模式(lazy mode)和迫切模式(eager mode)。 并发清理(Concurrent VACUUM)通常在内部…...

SSHv2公钥认证示例-Paramiko复用 Transport 连接
在 Paramiko 中复用 Transport 连接时,若要通过 公钥认证(而非密码)建立连接,需手动加载私钥并与 Transport 关联。以下是详细操作步骤及完整代码示例: 步骤 1:加载私钥文件 使用 RSAKey 或 Ed25519Key 类…...

华为5.7机考-最小代价相遇的路径规划Java题解
题目内容 输入描述 输出描述 示例: 输入: 2 1 2 2 1 输出: 3 思路: Dijkstra 算法实现 dijkstra(int sx, int sy, int[][] dirs) 方法: 参数:起点坐标 (sx, sy) 和允许的移动方向 初始化࿱…...

element-ui分页的使用及修改样式
1.安装 npm install element-ui -S 2.在main.js中引入,这里是全部引入,也可以按需引入 import ElementUI from element-ui import element-ui/lib/theme-chalk/index.css Vue.use(ElementUI) 3.使用 layout"prev, pager, next, jumper" :jumpe…...

[Unity]-[UI]-[Image] 关于UI精灵图资源导入设置的详细解释
Unity UI Sprite UI资源导入详解图片导入项目Texture TypeTexture ShapeAdvanced Setting 高级设置 图片设置案例常见细节问题 知识点详解来源 UI资源导入详解 Unity中的UI资源有图片、矢量图、字体、预制体、图集、动画等等资源。 这其中图片是最重要以及最基础的资源组成&a…...

MLX-Audio:高效音频合成的新时代利器
MLX-Audio:高效音频合成的新时代利器 现代社会的快节奏生活中,对语音技术的需求越来越高。无论是个性化语音助手,还是内容创作者所需的高效音频生成工具,语音技术都发挥着不可或缺的作用。今天,我们将介绍一个创新的开…...

操作系统导论——第27章 插叙:线程API
关键问题:如何创建和控制线程? 操作系统应该提供哪些创建和控制线程的接口?这些接口如何设计得易用和实用? 一、线程创建 编写多线程程序的第一步就是创建新线程,因此必须存在某种线程创建接口。在 POSIX 中࿱…...

代采系统:定义、优势与未来趋势
一、代采系统的定义 代采系统是一种基于互联网的集中采购平台,它通过整合供应链资源,为中小企业或个人提供采购代理服务。商家可以在没有自己库存的情况下销售产品,当客户下单时,订单信息会自动或手动发送给供应商,由…...
(c++))
后缀表达式+栈(详解)(c++)
前言 很抱歉,上一期没有介绍栈stack的用法,今天简要介绍一下,再讲讲后缀表达式,用stack栈做一些后缀表达式的练习。 栈 栈stack是c中系统给出的栈,有了它,就不用自己创建栈啦! 头文件 栈sta…...

Kaggle图像分类竞赛实战总结详细代码解读
前言 我是跟着李沐的动手学深度学习v2视频学习深度学习的,光看不做假把式,所以在学习完第七章-现代卷积神经网络之后,参加了一次李沐发布的Kaggle竞赛。自己动手,从组织数据集开始,到训练,再到推理&#x…...

开源AI对比--dify、n8n
原文网址:开源AI对比--dify、n8n-CSDN博客 简介 本文介绍开源AI工作流工具的选型。 对比 项difyn8n占优者学习难度简单中等dify核心理念用LLM构建应用。“连接一切”。以工作流自动化连接各系统。平手工作模式 Chatflow:对话。支持用户意图识别、上下…...

【SQL系列】多表关联更新
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
)
软件设计师教程——第一章 计算机系统知识(下)
前言 在竞争激烈的就业市场中,证书是大学生求职的重要加分项。中级软件设计师证书专业性强、认可度高,是计算机相关专业学生考证的热门选择,既能检验专业知识,又有助于职业发展。本教程将聚焦核心重点,以点带面构建知…...
系统软件部署全攻略:Redis、RabbitMQ、MySQL 等集群搭建指南)
华为银河麒麟 V10(ARM)系统软件部署全攻略:Redis、RabbitMQ、MySQL 等集群搭建指南
一、Redis 集群部署(主从 哨兵模式) 1. 环境准备 系统:华为银河麒麟 V10(ARM64)节点:3 台服务器(1 主 2 从 3 哨兵) 2. 安装包下载 bash # 华为镜像站 wget https://update.c…...

World of Warcraft [CLASSIC][80][Deluyia] [Fragment of Val‘anyr]
瓦兰奈尔的碎片 [Fragment of Valanyr] 有时候下个班打个游戏,没想到套路也这么多,唉,何况现实生活,这一个片版本末期才1000G,30个,也就30000G,时光徽章等同月卡15000G,折合一下也就…...

C++:求分数序列和
【描述】 有一个分数序列 2/1,3/2,5/3,8/5,13/8,21/13,.... 求这个分数序列的前n项之和。 输入 输入有一行:正整数n。 输出 输出有一行:分数序列的和(浮点数,精确到小数点后4位)。 【样例输入】 99 【样例输出】 160.4…...

支付宝沙盒模式商家转账经常出现 响应异常: 解包错误
2025年5月9日16:27:08 php8.3 laravel11 octane swoole加速 测试时不时就出现 响应异常: 解包错误 错误信息: Yansongda\Artful\Exception\InvalidResponseException: 响应异常: 解包错误 in /opt/www/vendor/yansongda/artful/src/Direction/CollectionDirect…...
