当前位置： 首页 > news >正文

【递归，搜索与回溯算法篇】专题（一） - 递归

news 来源：原创 2025/8/10 1:14:55

在这里插入图片描述

文章目录

      • 面试题 08.06. 汉诺塔问题
      • 21. 合并两个有序链表
      • 206. 反转链表
      • 24. 两两交换链表中的节点
      • 50. Pow(x, n)

面试题 08.06. 汉诺塔问题

题目链接： 面试题 08.06. 汉诺塔问题
题目描述：

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例 1：

输入：A = [2, 1, 0], B = [], C = []
输出：C = [2, 1, 0]

示例 2：

输入：A = [1, 0], B = [], C = []
输出：C = [1, 0]

提示：

A 中盘子的数目不大于 14 个。

题目解析：

  • 小规模问题分析

当N = 1时：直接移动

//将盘子直接从a移动到c
a -> c

在这里插入图片描述
当N = 2时:先将最小的盘子从a移到b,再将大盘从a移到c,再将小盘从b移到c。

//先把小盘子从a移动到b
a -> b
//再把大盘子从a移动到c
a -> c
//最后把小盘子从b移动到c
b -> c

在这里插入图片描述
当N = 3时：先将前两个盘子借助c从a移动到b,再将最大的盘子移动到c，将前两个盘子借助a从b移动到c。

//将前两个盘子从a移动到b(借助c)
a -> c
a -> b
c -> b
//将最大的盘子从a移动到c
a -> c
//将b上面的两个盘子从b移动到c(借助a)
b -> a
b -> c
a -> c

在这里插入图片描述

  • 这道题为什么可以使用递归？
    解决大问题时出现了相同的子问题，在解决子问题时又出现了相同的子问题。
  • 如何编写递归代码？
    1.重复子问题 -> 函数头
    函数头：将x柱子上的一堆盘子，借助y柱子，转移到z柱子上。n代表盘子的数量
    void dfs(x , y , z , int n )
    2.只关心某一个子问题在做什么 -> 函数体
    函数体：
    将x柱子上的n-1个盘子借助z柱子放到y柱子上
    dfs(x , z , y , n-1)
    将x柱子最大的盘子放到z柱子上
    x.back() -> z
    将y柱子上的n-1个盘子借助x盘子放到z柱子上
    dfs(y , x , z , n-1)
    当剩最后一个盘子时，直接从a柱子移动到c柱子
    x.back -> z

代码实现：

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n){if(n == 1){C.push_back(A.back());A.pop_back();return;}dfs(A,C,B,n-1);C.push_back(A.back());A.pop_back();dfs(B,A,C,n-1);}
};

21. 合并两个有序链表

题目链接： 21. 合并两个有序链表
题目描述：
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

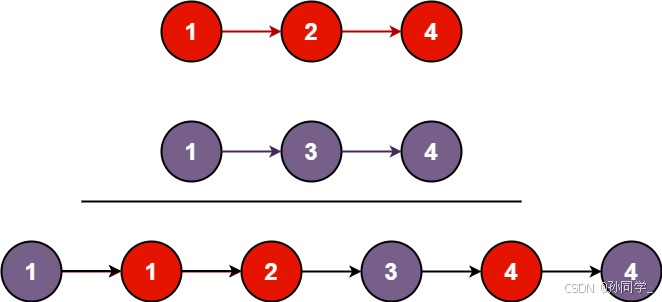
在这里插入图片描述

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

  • 两个链表的节点数目范围是 [0, 50]
  • -100 <= Node.val <= 100
  • l1 和 l2 均按 非递减顺序 排列

题目解析：
这道题让我们将两个升序链表合并为一个新的升序链表，我们用递归的解法就是先找出l1和l2头节点小的那一个，让它作为新的链表的头节点。然后在剩下的两个链表中继续去找小的那个作为链表的头节点。此时就出现了相同的子问题。

  • 相同的子问题 -> 函数头的设计
    Node* dfs(Node* l1,Node* l2)
  • 某个子问题在干什么 -> 函数体的设计
    先判断两个头指针的大小，谁小谁当最后的头指针
    ①比大小
    ②让小的那个连接剩下的两个链表合并后的结果
    小->next = dfs(小->next,大)
    return 小；
  • 递归的出口
    谁为空返回另一个

代码实现：

class Solution 
{
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2){if(l1 == nullptr) return l2;if(l2 == nullptr) return l1;if(l1 -> val <= l2 -> val){l1 -> next = mergeTwoLists(l1 -> next,l2);return l1;}else{l2 -> next = mergeTwoLists(l1,l2 -> next);return l2;}}
};

206. 反转链表

题目链接： 206. 反转链表
题目描述：

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：
在这里插入图片描述
输入： head = [1,2,3,4,5]
输出： [5,4,3,2,1]

示例 2：
在这里插入图片描述
输入： head = [1,2]
输出： [2,1]

示例 3：

输入： head = []
输出：[]

题目解析：
这道题给了我们一个单链表的头节点，让我们反转链表，然后返回反转后的链表。
第一种视角：从宏观的角度来看待这个问题
将head的next的next指向head，将head的next置为空。
如此我们会发现这将会导致结点丢失
在这里插入图片描述
比如上述操作会使得3这个结点丢失。
我们用递归的方法来解决这道问题
1.我们先让当前结点后面的链表先逆置，并且把头节点返回。
2.把当前结点添加到逆置后的结点的后面即可。
第二种视角：将链表看成一棵树
链表其实是一种特殊的树形结构，仅需对链表做一次深度优先遍历即可。
在这里插入图片描述

我们定义一个newhead对链表做一次深度优先遍历，当newhead的next为空时说明此结点就是将来要返回的头节点

  • 重复子问题 -> 函数头的设计
    传入一个头节点，从后向前反转链表
  • 子问题在干什么 -> 函数体的设计
    将此结点的next的next指向此节点，此节点的next置为空
  • 返回值
    返回next为空的结点

代码实现：

class Solution {
public:ListNode* newhead; //定义一个newhead记录要返回的新的头节点ListNode* reverseList(ListNode* head) {if(head == nullptr || head -> next == nullptr) return head;auto newhead = reverseList(head -> next);head -> next -> next = head;head -> next = nullptr;return newhead;}
};

24. 两两交换链表中的节点

题目链接： 24. 两两交换链表中的节点
题目描述：
给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：
在这里插入图片描述
输入： head = [1,2,3,4]
输出： [2,1,4,3]

示例 2：

输入： head = []
输出： []

示例 3：

输入： head = [1]
输出： [1]

题目解析：
这道题目让我们两两交换相邻的节点，并返回交换后链表的头节点，前提是在不修改节点中的值的情况下，即只能进行节点交换。这道题我们可以用递归的思路来求解。首先定义一个ret来用来接收交换后链表的头节点。然后把相邻节点进行两两交换。

代码实现：

class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;//如果链表为空或者链表的下一个节点为空，直接返回头节点ListNode* r = swapPairs(head->next->next);ListNode* ret = head->next;head->next->next = head;head->next = r;return ret;}
};

50. Pow(x, n)

题目链接： 50. Pow(x, n)
题目描述：

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，x的n次方）。

示例 1：

输入： x = 2.00000, n = 10
输出： 1024.00000

示例 2：

输入： x = 2.10000, n = 3
输出： 9.26100

示例 3：

输入： x = 2.00000, n = -2
输出： 0.25000
解释： 2-2 = 1/22 = 1/4 = 0.25

题目解析：
这道题让我们计算x的n次方。
解法一： 暴力解法
我们可以用一个循环进行暴力求解，但是对这道题而言暴力求解会超出时间限制。
解法二： 快速幂
实现快速幂的方法有两种，第一种是递归，第二种是循环。本题我们就来用递归的方式实现快速幂。
例如：我们要求3的16次方，我们可以先求出3的8次方，要求3的8次方，我们可以先求出3的4次方，要求3的4次方，我们可以先求出3的平方。
在这里插入图片描述
当n为奇数时，我们可以先求出x的二分之n次方，最后再乘上x。
在这里插入图片描述

  • 相同的的子问题 -> 函数头的设计
    给一个数和一个指数，求出x的n次幂是多少
    int Pow( x , n )
  • 只关心某一层在干什么 -> 函数体的设计
    给一个数和一个指数，求出x的n/2次幂是多少
    tmp = Pow( x , n / 2 )
  • 返回值
    分类讨论
    如果n为偶数，返回tmp*tmp
    如果n为奇数，返回tmp*tmp*x

代码实现：

class Solution
{
public:double myPow(double x, int n) {return n < 0 ? 1.0 / pow(x, -(long long)n) : pow(x,n); }double pow(double x, long long n){if(n == 0) return 1.0;double tmp = pow(x ,n / 2);return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;}
};

👍 如果对你有帮助，欢迎：

  • 点赞 ⭐️
  • 收藏 📌
  • 关注 🔔

相关文章：

【递归，搜索与回溯算法篇】专题（一） - 递归

文章目录 面试题 08.06. 汉诺塔问题21. 合并两个有序链表206. 反转链表24. 两两交换链表中的节点50. Pow(x, n) 面试题 08.06. 汉诺塔问题 题目链接&#xff1a; 面试题 08.06. 汉诺塔问题 题目描述&#xff1a; 在经典汉诺塔问题中&#xff0c;有 3 根柱子及 N 个不同大小的…...

编程日记 2025/8/10 1:14:55

B站pwn教程笔记-9

前言&#xff1a;可以去一些开源镜像站下载libc老的乌班图镜像&#xff0c;因为堆题的libc可能比较老&#xff0c;没有新的一些保护措施和机制。 格式化字符串漏洞 归根结底&#xff0c;可以读写任意地址内存。 泄露栈数据/任意地址数据 主要问题就是printf不知道自己有没有…...

编程日记 2025/8/5 21:32:53

NVR（网络视频录像机） 和 网络摄像机（IPC，IP Camera）

NVR&#xff08;网络视频录像机&#xff09; 和 网络摄像机&#xff08;IPC&#xff0c;IP Camera&#xff09; 是网络监控系统的两个核心组件&#xff0c;但功能定位完全不同。以下是它们的核心区别&#xff1a; 1. 功能角色 组件网络摄像机&#xff08;IPC&#xff09;NVR&a…...

编程日记 2025/8/6 11:17:04

数智读书笔记系列032《统一星型模型--一种敏捷灵活的数据仓库和分析设计方法》

引言 在当今数字化时代，数据仓库作为企业数据管理的核心基础设施，承担着整合、存储和提供企业数据的关键角色。随着商业环境的快速变化和业务需求的日益复杂，数据仓库的设计方法也在不断演进，以适应新的挑战和要求。 背景与意义 数据仓库领域长期存在着两种主流方法论之…...

编程日记 2025/8/10 1:12:25

互联网大厂Java求职面试：基于RAG的智能问答系统设计与实现

互联网大厂Java求职面试&#xff1a;基于RAG的智能问答系统设计与实现 场景背景 在某互联网大厂的技术面试中&#xff0c;技术总监张总正在面试一位名为郑薪苦的求职者。郑薪苦虽然对技术充满热情&#xff0c;但回答问题时总是带着幽默感&#xff0c;有时甚至让人哭笑不得。 …...

编程日记 2025/8/10 1:09:33

[C#]Task.Run()和Task.Factory.StartNew()对比（腾讯元宝）

Task.Run和Task.Factory.StartNew都是用来创建并启动任务的方法&#xff0c;但它们的内部实现和使用场景有所不同。两者的主要区别&#xff1a;默认调度器、配置选项、异常处理、适用场景。建议用户大多数情况下使用Task.Run&#xff0c;除非需要StartNew的高级配置&#xff0c…...

编程日记 2025/8/10 1:09:32

Java游戏服务器开发流水账(3)游戏数据的缓存简介

简介 游戏服务器数据缓存是一种在游戏服务器运行过程中&#xff0c;用于临时存储经常访问的数据的技术手段&#xff0c;旨在提高游戏性能、降低数据库负载以及优化玩家体验。游戏开发中数据的缓存可以使用Java自身的内存也可以使用MemCache&#xff0c;Redis&#xff0c;注意M…...

编程日记 2025/8/10 1:12:14

PostgreSQL可见性映射VM

1.可见性映射 清理过程的代价高昂&#xff0c;为了减小清理的开销&#xff0c;在PostgreSQL 8.4版中引入了VM。 VM的基本概念很简单。 每个表都拥有各自的可见性映射&#xff0c;用于保存表文件中每个页面的可见性。 页面的可见性确定了每个页面是否包含死元组。清理过程可以…...

编程日记 2025/8/3 10:26:54

集成电路流片随笔26：tinyriscv的三级流水线细则pc

include "defines.v"// PC寄存器模块 module pc_reg(input wire clk,input wire rst,input wire jump_flag_i, // 跳转标志input wire[InstAddrBus] jump_addr_i, // 跳转地址input wire[Hold_Flag_Bus] hold_flag_i, // 流水线暂停标志input wire…...

编程日记 2025/8/3 10:26:52

如何解决Jmeter中的乱码问题？

在 JMeter 中遇到乱码问题通常是由于字符编码不一致导致的&#xff0c;常见于 HTTP 请求响应、参数化文件读取、报告生成等场景。以下是系统化的解决方案&#xff1a; 1. HTTP 请求响应乱码 原因&#xff1a; 服务器返回的字符编码&#xff08;如UTF-8、GBK&#xff09;与 J…...

编程日记 2025/8/5 16:40:24

TextRNN 模型实现微博文本情感分类

在自然语言处理&#xff08;NLP&#xff09;领域&#xff0c;文本情感分类是一项极具应用价值的任务。它能帮助企业分析用户反馈、社交媒体舆情监测等。本文将通过一段实际代码&#xff0c;带大家了解如何利用 PyTorch 框架和 TextRNN 模型&#xff0c;完成微博文本的情感分类工…...

编程日记 2025/8/3 10:26:48

支付宝 SEO 优化：提升小程序曝光与流量的完整指南

在拥有庞大用户基数的支付宝平台上&#xff0c;小程序已成为商家触达用户、提供服务的重要渠道。然而&#xff0c;随着平台上小程序数量的快速增长&#xff0c;如何在激烈的竞争中脱颖而出&#xff0c;获得更多的曝光和流量&#xff0c;成为每个开发者和运营者必须面对的关键挑…...

编程日记 2025/8/3 10:26:46

基于WSL用MSVC编译ffmpeg7.1

在windows平台编译FFmpeg&#xff0c;网上的大部分资料都是推荐用msys2mingw进行编译。在win10平台&#xff0c;我们可以采用另一种方式&#xff0c;即wslmsvc 实现window平台的ffmpeg编译。 下面将以vs2022ubuntu22.04 为例&#xff0c;介绍此方法 0、前期准备 安装vs2022 &…...

编程日记 2025/8/5 13:15:56

高并发内存池（二）：项目的整体框架以及Thread_Cache的结构设计

目录 前言 一&#xff0c;项目整体框架设计 二&#xff0c;thread cache结构设计 模拟定长内存池的设计思路 采用一定的对齐规则设计 thread cache大致框架 申请内存Allocate方法 1&#xff0c;thread cache 哈希桶的内存对齐规则 2&#xff0c;内存对齐规则代码实现 …...

编程日记 2025/8/3 10:26:42

K8S扩缩容及滚动更新和回滚

目录&#xff1a; 1、滚动更新1、定义Deployment配置2、应用更新 2、版本回滚1. 使用kubectl rollout undo命令 3、更新暂停与恢复1、暂停更新2、更新镜像&#xff08;例如&#xff0c;使用kubectl set image命令&#xff09;3、恢复更新 4、弹性扩缩容1、扩容命令2、缩容命令3…...

编程日记 2025/8/3 10:26:40

K8S - GitLab CI 自动化构建镜像入门

一、引言 在现代持续交付&#xff08;CI/CD&#xff09;体系中&#xff0c;容器镜像的自动化构建与推送已成为交付链条的重要一环。 GitLab CI/CD 作为 GitLab 平台的原生集成功能&#xff0c;提供了声明式、可扩展的流水线机制&#xff0c;使得开发者可以在代码生命周期内实…...

编程日记 2025/8/3 10:26:38

万兴PDF-PDFelement v11.4.13.3417

万兴PDF专家(Wondershare PDFelement)是一款国产PDF文档全方位解决方案.万兴PDF编辑器软件万兴PDF中文版,专注于PDF的创建,编辑,转换,签名,压缩,合并,比较等功能.万兴PDF专业版PDF编辑软件,以简约风格及强大的功能在国外名声大噪,除了传统功能外,还提供OCR扫描,表格识别,创建笔…...

编程日记 2025/8/8 16:27:03

4.2【LLaMA-Factory实战】金融财报分析系统：从数据到部署的全流程实践

【LLaMA-Factory实战】金融财报分析系统&#xff1a;从数据到部署的全流程实践 一、引言 在金融领域&#xff0c;财报分析是投资决策的核心环节。传统分析方法面临信息提取效率低、风险识别不全面等挑战。本文基于LLaMA-Factory框架&#xff0c;详细介绍如何构建一个专业的金…...

编程日记 2025/8/8 6:19:34

Vue Router 3 使用详解：从零构建嵌套路由页面

Vue Router 是 Vue.js 官方的路由管理器&#xff0c;常用于构建单页面应用&#xff08;SPA&#xff09;。本文将手把手带你完成 vue-router3.6.5 的基本配置&#xff0c;并实现一个带有嵌套路由的页面结构。本文适用于 Vue 2.x 项目 一、安装 vue-router3.6.5 npm install vue…...

编程日记 2025/8/3 10:26:32

ChatGPT深度研究功能革新：GitHub直连与强化微调

目录 一、ChatGPT深度研究功能迎来革命性更新 1.1 GitHub直连功能详解 1.2 强化微调(RTF)正式发布 二、GitHub直连功能深度体验 2.1 实际应用场景演示 2.2 技术实现原理探讨 三、强化微调技术解析 3.1 RTF技术核心优势 3.2 适用场景分析 四、开发者反馈与行业影响 4…...

编程日记 2025/8/6 17:38:08

【Ansible】模块详解

一、ansible概述 1.1 ansible介绍 Ansible 是一个基于 Python 开发的配置管理和应用部署工具&#xff0c;近年来在自动化管理领域表现突出。它集成了许多传统运维工具的优点&#xff0c;几乎可以实现 Pubbet 和 Saltstack 所具备的功能。 1.2 ansible能做什么 批量处理。An…...

编程日记 2025/8/3 10:26:28

深入理解C/C++内存管理：从基础到高级优化实践

一、内存区域划分与基础管理机制​​ ​​栈&#xff08;Stack&#xff09;​​ 栈由系统自动管理&#xff0c;用于存储函数调用时的局部变量、参数及返回地址。其特点是高效但空间有限&#xff08;通常1-8MB&#xff09;&#xff0c;遵循后进先出&#xff08;LIFO&#xff09;…...

编程日记 2025/8/6 16:24:01

两台服务器之前共享文件夹

本文环境 服务器A:ubuntu24.22系统 IP:10.0.8.1 服务器B:ubuntu24.22系统 IP:10.0.8.10 本操作旨在将服务器B的/opt/files目录共享给服务器A得/opt/files 在 B 服务器上设置共享 安装 NFS 服务&#xff1a; sudo apt -y install nfs-kernel-server编辑/etc/exports文件&…...

编程日记 2025/8/3 10:26:24

stm32之USART

目录 1.引入1.1 通信接口1.2 串口 2.USART2.1 简介2.2 框图2.3 基本机构图2.4 数据帧2.5 波特率发生器2.6 数据包2.6.1 数据模式2.6.2 HEX数据包2.6.3 文本数据包2.6.4 HEX数据包接收2.6.5 文本数据包接收 3.结构体和相关API3.1 结构体3.2 API3.2.1 **初始化相关函数**void USA…...

编程日记 2025/8/3 10:26:22

使用 systemd 管理 Linux 服务：配置与自动重启指南

使用 systemd (推荐&#xff0c;适用于大多数 Linux 发行版) systemd 是现代 Linux 系统中最常用的服务管理器。它能可靠地管理进程&#xff0c;并在进程崩溃时自动重启。 创建 systemd 服务文件&#xff1a; 创建一个文件&#xff0c;例如 /etc/systemd/system/app.service…...

编程日记 2025/8/4 3:33:52

【计算机视觉】Car-Plate-Detection-OpenCV-TesseractOCR：车牌检测与识别

Car-Plate-Detection-OpenCV-TesseractOCR&#xff1a;车牌检测与识别技术深度解析 在计算机视觉领域&#xff0c;车牌检测与识别&#xff08;License Plate Detection and Recognition, LPDR&#xff09;是一个极具实用价值的研究方向&#xff0c;广泛应用于智能交通系统、安…...

编程日记 2025/8/3 10:26:20

《Spring Boot 3.0全新特性详解与实战案例》

大家好呀&#xff01;今天让我们轻松掌握Spring Boot 3.0的所有新特性&#xff01;&#x1f680; &#x1f4cc; 第一章&#xff1a;Spring Boot 3.0简介 1.1 什么是Spring Boot 3.0&#xff1f; Spring Boot 3.0就像是Java开发者的"超级工具箱"&#x1f9f0;&…...

编程日记 2025/8/9 12:34:12

二叉树的深度

二叉树的深度是指从根节点到叶子节点的最长路径上的节点数。 一、最大深度 104. 二叉树的最大深度 - 力扣&#xff08;LeetCode&#xff09; 最大深度是指从根节点到最远叶子节点的最长路径上的节点数。 //递归法 /*** Definition for a binary tree node.* public class T…...

编程日记 2025/8/4 3:33:47

科技创业园共享会议室线上预约及智能密码锁系统搭建指南

为科技创业园区的运营管理者&#xff0c;我深知高效利用会议室资源的重要性。2023年第三季度&#xff0c;我们园区启动会议室智能化改造项目&#xff0c;经过三个月的实践&#xff0c;成功将32间共享会议室升级为"线上预约智能门锁"管理模式。现将改造经验分享如下&a…...

编程日记 2025/8/4 3:33:45

自定义prometheus exporter实现监控阿里云RDS

# 自定义 Prometheus Exporter 实现多 RDS 数据采集## 背景1. Prometheus 官网提供的 MySQL Exporter 对于 MySQL 实例只能一个进程监控一个实例&#xff0c;数据库实例很多的情况下&#xff0c;不方便管理。 2. 内部有定制化监控需求&#xff0c;RDS 默认无法实现&#xff0c;…...

编程日记 2025/8/9 11:19:29

LeetCode 3342.到达最后一个房间的最少时间 II：dijkstra算法(和I一样)

【LetMeFly】3342.到达最后一个房间的最少时间 II&#xff1a;dijkstra算法(和I一样) 力扣题目链接&#xff1a;https://leetcode.cn/problems/find-minimum-time-to-reach-last-room-ii/ 有一个地窖&#xff0c;地窖中有 n x m 个房间&#xff0c;它们呈网格状排布。 给你一…...

编程日记 2025/8/4 3:33:40

iOS创建Certificate证书、制作p12证书流程

一、创建Certificates 1、第一步得先在苹果电脑上创建一个.certSigningRequest的文件。首先打开钥匙串&#xff0c;使用快捷键【command空格】——输入【钥匙串】回车&#xff08;找不到就搜一下钥匙串访问使用手册&#xff09; 2、然后在苹果电脑的左上角菜单栏选择【钥匙串…...

编程日记 2025/8/5 12:28:40

特殊配合力（SCA）作为全基因组关联分析（GWAS）的表型，其生物学意义和应用价值

生物学意义 解析非加性遗传效应 特殊配合力（SCA）主要反映特定亲本组合的杂交优势，由非加性遗传效应（如显性、超显性、上位性）驱动。显性效应涉及等位基因间的显性互作，上位性效应则涉及不同位点间的基因互作。通过SCA-GWAS，可以定位调控这些非加性效应的关键基因组区域…...

编程日记 2025/8/4 3:33:37

Python实例题：Python快速获取斗图表情

目录 Python实例题 题目 python-get-meme-imagesPython 快速获取斗图表情脚本 代码解释 get_meme_images 函数&#xff1a; download_images 函数&#xff1a; 主程序&#xff1a; 运行思路 注意事项 Python实例题 题目 Python快速获取斗图表情 python-get-meme-im…...

编程日记 2025/8/4 3:33:35

探索表访问方法功能：顺序扫描分析

引言 在之前的文章中&#xff0c;我们讨论了 PostgreSQL 表访问方法 API 的基础知识以及堆元组&#xff08;heap tuple&#xff09;与元组表槽&#xff08;Tuple Table Slot&#xff0c;简称 TTS&#xff09;之间的区别。 本文将深入探讨 PostgreSQL 核心如何通过特定的 API …...

编程日记 2025/8/4 3:33:33

RISC-V CLINT、PLIC及芯来ECLIC中断机制分析 —— RISC-V中断机制（一）

在长期的嵌入式开发实践中&#xff0c;对中断机制的理解始终停留在表面层次&#xff0c;特别当开发者长期局限于纯软件抽象层面时&#xff0c;对中断机制的理解极易陷入"知其然而不知其所以然"的困境&#xff0c;这种认知的局限更为明显&#xff1b;随着工作需要不断…...

编程日记 2025/8/8 23:20:10

Idea Code Templates配置

Templates配置 配置位置模板案例 配置位置 Settings->Editor->File and Code Templates模板案例 #if (${PACKAGE_NAME} && ${PACKAGE_NAME} ! "")package ${PACKAGE_NAME};#endimport com.ktools.common.dataprocess.DataProcess; import com.ktools…...

编程日记 2025/8/4 3:33:28

fakebook

解题方法&#xff1a; 一.用御剑扫描后台&#xff0c;查看robot.txt文件&#xff0c;发现是一个/user.php.bak,备份文件&#xff0c;我们访问这个文件 <?phpclass UserInfo {public $name "";public $age 0;public $blog "";public function __co…...

编程日记 2025/8/5 16:26:25

英伟达Blackwell架构重构未来：AI算力革命背后的技术逻辑与产业变革

——从芯片暴力美学到分布式智能体网络&#xff0c;解析英伟达如何定义AI基础设施新范式 开篇&#xff1a;当算力成为“新石油”&#xff0c;英伟达的“炼油厂”如何升级&#xff1f; 2025年3月&#xff0c;英伟达GTC大会上&#xff0c;黄仁勋身披标志性皮衣&#xff0c;宣布了…...

编程日记 2025/8/4 3:33:24

用 Rust 搭建一个优雅的多线程服务器：从零开始的详细指南

嘿&#xff0c;小伙伴们&#xff01;今天咱们来聊聊怎么用 Rust 搭建一个牛气哄哄的多线程服务器&#xff0c;还能在需要的时候优雅地关机。为啥要用 Rust 呢&#xff1f;因为 Rust 是个超级靠谱的语言&#xff0c;它能保证内存安全&#xff0c;写并发代码的时候不用担心那些让…...

编程日记 2025/8/4 3:33:22

今日行情明日机会——20250509

上证指数今天缩量&#xff0c;整体跌多涨少&#xff0c;走势处于日线短期的高位~ 深证指数今天缩量小级别震荡&#xff0c;大盘股表现更好~ 2025年5月9日涨停股主要行业方向分析 一、核心主线方向 服装家纺&#xff08;消费复苏出口链驱动&#xff09; • 涨停家数&#xf…...

编程日记 2025/8/4 3:33:20

ESP32开发入门(七)：HTTP开发实践

一、HTTP协议基础 1.1 什么是HTTP&#xff1f; HTTP&#xff08;HyperText Transfer Protocol&#xff0c;超文本传输协议&#xff09;是互联网上应用最为广泛的一种网络协议&#xff0c;用于从服务器传输超文本到本地浏览器。它是一种无状态的请求/响应协议&#xff0c;工作…...

编程日记 2025/8/4 3:33:18

【强化学习】强化学习算法 - 马尔可夫决策过程

马尔可夫决策过程 (Markov Decision Process, MDP) 1. MDP 原理介绍 马尔可夫决策过程 (MDP) 是强化学习 (Reinforcement Learning, RL) 中用于对序贯决策 (Sequential Decision Making) 问题进行数学建模的标准框架。它描述了一个智能体 (Agent) 与环境 (Environment) 交互的…...

编程日记 2025/8/7 21:50:10

数据结构【二叉搜索树（BST)】

二叉搜索树 1. 二叉搜索树的概念2. 二叉搜索树的性能分析3.二叉搜索树的插入4. 二叉搜索树的查找5. 二叉搜索树的删除6.二叉搜索树的实现代码7. 二叉搜索树key和key/value使用场景7.1 key搜索场景&#xff1a;7.2 key/value搜索场景&#xff1a; 1. 二叉搜索树的概念 二叉搜索…...

编程日记 2025/8/4 3:33:13

振动临近失效状态，怎么频谱会是梳子？

这是一个破坏性试验的终末期振动波形。左边时域&#xff0c;右边频域。这是咋回事&#xff0c;时域看起来原本很正常的冲击信号&#xff0c;怎么频域是那个鬼样子。 同一组波形&#xff0c;放大后的频域 - 低频部分&#xff1a; 一个解释&#xff1a;...

编程日记 2025/8/4 3:33:11

橡胶制品行业质检管理的痛点 质检LIMS如何重构橡胶制品质检价值链

橡胶制品广泛应用于汽车、医疗、航空等领域&#xff0c;其性能稳定性直接关联终端产品的安全性。从轮胎耐磨性测试到密封件耐腐蚀性验证&#xff0c;每一项检测数据都是企业参与市场竞争的核心筹码。然而&#xff0c;传统实验室管理模式普遍面临设备调度混乱、检测流程追溯断层…...

编程日记 2025/8/6 19:31:35

【CTFSHOW_Web入门】命令执行

文章目录 命令执行web29web30web31web32web33web34web35web36web37web38web39web40web41web42web43web44web45web46web47web48web49web50web51web52web53web54web55web56web57web58web59web60web61web62web63web64web65web66web67web68web69web70web71web72web73web74web75web7…...

编程日记 2025/8/4 3:33:06

三维底座+智能应用，重构城市治理未来

在“数字中国”战略的引领下&#xff0c;住房和城乡建设领域正迎来一场深刻的数字化转型浪潮。2024年《“数字住建”建设整体布局规划》的发布&#xff0c;明确提出以“CIM”&#xff08;城市信息模型&#xff09;为核心&#xff0c;构建城市三维数字底座&#xff0c;推动住建行…...

编程日记 2025/8/4 3:33:03

养生：塑造健康生活的良方

养生是一场贯穿生活的自我关爱行动&#xff0c;从饮食、运动、睡眠到心态调节&#xff0c;每一个环节都对健康有着深远影响。以下为你带来全面且实用的养生策略。 饮食养生&#xff1a;科学搭配&#xff0c;呵护肠胃 合理规划三餐&#xff0c;遵循 “早营养、午均衡、晚清淡”…...

编程日记 2025/8/4 3:33:01

docker 镜像的导出和导入（导出完整镜像和导出容器快照）

一、导出原始镜像 1. 使用 docker save 导出完整镜像 适用场景&#xff1a;保留镜像的所有层、元数据、标签和历史记录&#xff0c;适合迁移或备份完整镜像环境。 操作命令 docker save -o <导出文件名.tar> <镜像名:标签>示例&#xff1a;docker save -o milvu…...

编程日记 2025/8/4 3:32:59