当前位置：首页 > news >正文

数据结构*二叉树

news 来源：原创 2025/8/13 9:56:38

树

树是一种非线性数据结构。
在这里插入图片描述
这就是抽象的树的结构。
对于一棵树来说，有N个结点，就有N-1条边

其中有许多概念：

根结点：对于上图来说就是A
子树：就是结点下面分开的部分。例如：A的子树就是以B为根结点的树和以C为根结点的树。
结点的度：就是这个节点含有子树的个数称为该节点的度。
树的度：就是这棵树所有节点的度的最大值。上图的树的度为3
叶子结点或终端结点：度为0的结点。例如：D、E、I、G、H
层次：根节点为第一层。
树的高度或深度：树的最大层次。例如：上图就是4
当然还有许多概念，可以自行查找

树的表示方法

对于树的表示方法有很多种，如：双亲表示法，孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。下面是孩子兄弟表示法。
在这里插入图片描述

二叉树

什么是二叉树

二叉树就是特殊的一种树，其每个结点最多有两棵子树，即结点的度最大为 2 。对于二叉树来说，左子树和右子树有严格顺序之分，次序不能颠倒。如下图所示：
在这里插入图片描述
当然还有一些特殊的二叉树：满二叉树、完全二叉树。
满二叉树通俗来讲就是每一层的结点都是满的二叉树，如下图所示：

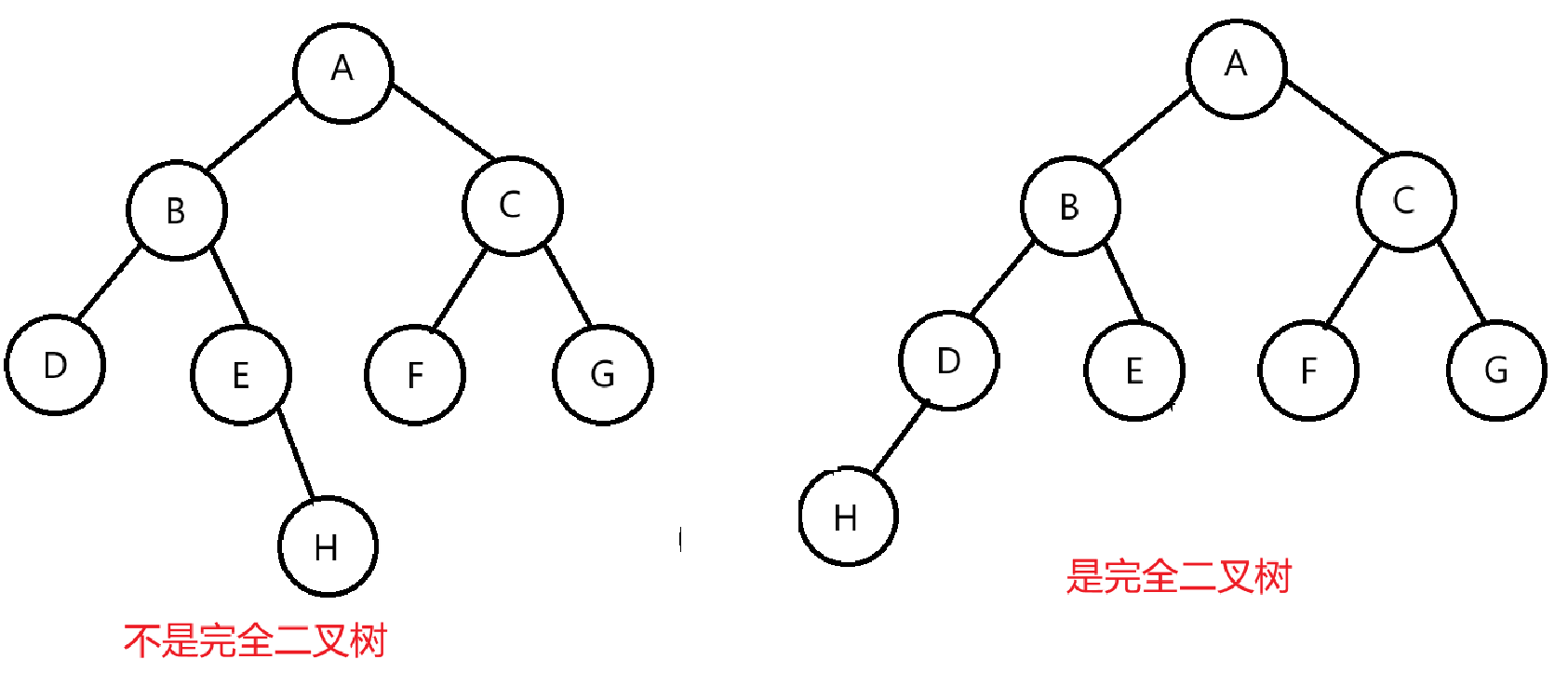
完全二叉树通俗来讲就是只有最后一层不是满的，其余层都是满的。但是最后一层的节点都是从最左边开始排，不会在中间空着。如下图所示：
在这里插入图片描述

二叉树的一些性质

1、一颗非空二叉树的第i层上最多有2^(i-1)个结点。
2、一颗深度为k的二叉树，其树的最大结点为2^k-1
3、由第二条性质推出，具有n个结点的完全二叉树的深度k = log(n+1) [以2为底的log] 向上取整。
4、对于任意一颗二叉树，其叶子结点为n0(结点度为0)，度为2的结点个数为n2，则n0 = n2 + 1。
5、对于具有n个结点的完全二叉树，按照从上到下、从左到右的顺序从0开始编号，则对于序号i的结点：
左孩子结点下标为2i + 1，当2i + 1 > n 时，就不存在左孩子结点。
右孩子结点下标为2i + 2，当2i + 2 > n 时，就不存在右孩子结点。
其父亲结点的下标为(i - 1) / 2。i == 0时，其结点为根节点，没有父亲结点。

二叉树的存储

二叉树的存储方式主要有两种，分别是顺序存储和链式存储。顺序存储是把二叉树的节点按照层次依次存于数组中。链式存储是通过节点类来构建二叉树。
下面是用孩子表示法来构建二叉树

static class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}
}

二叉树的遍历

对于二叉树的遍历有四种：前序遍历、中序遍历、后序遍历、层序遍历。
下面遍历一这棵二叉树为例：
在这里插入图片描述

层序遍历

1、层序遍历就是从上到下从左到右开始访问结点。
在这里插入图片描述
输出为：A B C D E F G H
下面我们重点来说明前中后序遍历！ 对于这三种遍历的过程就好像递归一样，始终重复完成某一操作。

前序遍历

2、前序遍历就是按照先访问根，再访问左子树，最后访问右子树。在访问根的时候输出。
在这里插入图片描述
对应的流程如上图所示：按照根 -> 左子树 -> 右子树的访问顺序
输出为：A B D E H C F G

代码展示：

public void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);
}

代码解释：

代码采用递归的方式，将问题化成子问题，就是访问根，打印根，访问左树(root.left)，访问右树(root.right)。结束条件就是当root为空时，直接返回，说明已经访问到底了（这颗树已经访问完了）。

中序遍历

3、中序遍历就是按照先访问左子树，再访问根，最后访问右子树。在访问根的时候输出。
在这里插入图片描述
对应的流程如上图所示：按照左子树 -> 根 -> 右子树的访问顺序
输出为：D B E H A F C G

代码展示：

public void inOrder(TreeNode root){if(root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);
}

代码解释：

代码采用递归的方式，将问题化成子问题，就是访问左树(root.left)，访问根，打印根，访问右树(root.right)。结束条件就是当root为空时，直接返回，说明已经访问到底了（这颗树已经访问完了）。

后序遍历

4、后序遍历就是按照先访问左子树，再访问右子树，最后访问根。在访问根的时候输出。
在这里插入图片描述
对应的流程如上图所示：按照左子树 -> 右子树 -> 根的访问顺序
输出为：D H E B F G C A

代码展示：

public void postOrder(TreeNode root){if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");
}

代码解释：

代码采用递归的方式，将问题化成子问题，就是访问左树(root.left)，访问右树(root.right)，访问根，打印根。结束条件就是当root为空时，直接返回，说明已经访问到底了（这颗树已经访问完了）。

二叉树的一些简单操作

求结点个数

代码展示：

// 获取树中节点的个数
private static int size= 0;
public int size1(TreeNode root) {//用计数的方式 -> 遍历if(root == null) {return 0;}size++;size1(root.left);size1(root.right);return size;
}
public int size(TreeNode root) {//子问题 -> 树的结点 = 左子树的结点 + 右子树的结点 + 1（root）if(root == null) {return 0;}return size(root.left) + size(root.right) + 1;
}

代码解释：

有两种思路：
1、用遍历思路，访问一个结点就size++
2、子问题思路：利用递归，将问题变成了“树的结点 = 左子树的结点 + 右子树的结点 + 1”

求叶子结点个数

代码展示：

// 获取叶⼦节点的个数
private static int count = 0;
public int getLeafNodeCount1(TreeNode root){//遍历思路 -> 左右子树都为nullif(root == null) {return 0;}if(root.left == null && root.right == null) {count++;}getLeafNodeCount1(root.left);getLeafNodeCount1(root.right);return count;
}
public int getLeafNodeCount(TreeNode root){//子问题 -> 树的叶子结点 = 左子树的叶子节点 + 右子树的叶子节点if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
}

代码解释：

有两种思路：
1、用遍历思路，访问一个结点当满足条件是就count++。当root == null时，也就说明了这棵树为空，没有结点。
2、子问题思路：利用递归，将问题变成了“树的叶子结点 = 左子树的叶子节点 + 右子树的叶子节点”，当满足条件时就说明是一个叶子结点。

求第K层节点的个数

代码展示：

public int getKLevelNodeCount(TreeNode root,int k){//当root为null时，说明这棵树提前走完了，还没有到第k层，也就没有第k层的结点if(root == null) {return 0;}//递归结束条件，当k==1时，说明已经走到了第k层if(k == 1) {return 1;}return getKLevelNodeCount(root.left,k - 1) + getKLevelNodeCount(root.right,k - 1);
}

代码解释：

将问题转换为左子树第k层的个数+右子树第k层的个数。此时层数逐次递减（k-1）。遍历到第k层就结束遍历了。

求二叉树的高度

代码展示：

public int getHeight(TreeNode root){//子问题 -> 左子树与右子树深度的最大值 + 1（root）if(root == null) {return 0;}return Math.max(getHeight(root.left),getHeight(root.right)) + 1;
}

代码解释：

将问题转换为“左子树与右子树深度的最大值 + 1（根结点本身高度1）”

检测值为val的元素是否存在

代码展示：

public TreeNode find(TreeNode root, int val){//当root为null时，也就没有val，返回nullif(root == null) {return null;}//当匹配成功，就返回当前结点if(root.val == val) {return root;}//到这里说明没有匹配成功，访问左子树有没有TreeNode ret = find(root.left,val);//如果没有匹配成功，则ret为null//ret不为null，则返回找到的结点if(ret != null) {return ret;}//到这里说明左子树也都没有匹配成功ret = find(root.right,val);//开始在右子树找return ret;//找到了ret就是匹配的结点，没有就是null
}

代码解释：

也是利用递归，将问题换成“左子树找，再在右子树找”。

层序遍历

代码展示：

1、使用队列

public void levelOrder(TreeNode root){//当root为null时，就没有结点，直接返回if(root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();//创建队列，将结点存储到队列中//从父亲结点开始，放入队列中queue.offer(root);while (!queue.isEmpty()) {//当将二叉树中的元素全部pop，此时queue为空，层序遍历完了TreeNode cur = queue.poll();//将队列中最上面的元素取出System.out.print(cur.val+" ");//打印//将其输出的左边的结点存入队列中（不为空）if(cur.left != null){queue.offer(cur.left);}//将其输出的右边的结点存入队列中（不为空）if(cur.right != null){queue.offer(cur.right);}//最后再通过循环将所有的结点的左右依次存入队列中，输出。//A -> B C(A的左右) -> D E(B的左右) F G(C的左右) -> H(E的右)}
}

2、使用嵌套列表+队列

public List<List<Character>> levelOrderPlus(TreeNode root) {List<List<Character>> ret = new ArrayList<>();if(root == null) {return ret;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {//当将二叉树中的元素全部pop，此时queue为空，层序遍历完了List<Character> curRow = new ArrayList<>();//每层创建一个新的列表//用来判断每层的个数。从父亲结点A一个 -> 经过while(size != 0)循环，列表中存入B D两个元素，列表中个数也就是2 -> 同理依次类推int size = queue.size();//进行分行处理，while (size != 0){TreeNode cur = queue.poll();//将队列中最上面的元素取出curRow.add(cur.val);//将这一层的元素存入当前列表中//将其输出的左边的结点存入队列中（不为空）if(cur.left != null){queue.offer(cur.left);}//将其输出的右边的结点存入队列中（不为空）if(cur.right != null){queue.offer(cur.right);}size--;}ret.add(curRow);//将这一层的列表存入列表中}return ret;//返回这个二维列表
}

代码解释：

方法一是使用队列，利用队列先进先出的特点，先将父亲结点放进去，然后就开始向队列存放元素。（具体过程：首先从队列出元素并打印，存放出来元素的左结点和右结点）如下图所示：
在这里插入图片描述

方法二是多使用了嵌套列表，是为了更好的区分每层的元素。利用每次队列中的size，来创建列表，再存入列表中。如下图所示：
在这里插入图片描述

判断是否为完全二叉树

完全二叉树和层序遍历有关，思路和层序遍历差不多，但使用队列时候，是需要存入null值的，这样好判断在中间是不是空着的。

代码展示：

public boolean isCompleteTree(TreeNode root){if(root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();if(cur == null){break;}else {queue.offer(cur.left);queue.offer(cur.right);}}while (!queue.isEmpty()) {if(queue.poll() != null) {return false;}}return true;
}

代码解释：

这里不需要判断cur的左右是否为空，直接进队列即可。当出队列的为null，说明层序遍历到了null。如果这是一棵完全二叉树，则剩下的结点都为null，也就是队列中的元素全为null；当不是一棵完全二叉树，队列中的元素中必然有结点。后面的while循环就是用来判断队列中是否全为null。

树

其中有许多概念：

树的表示方法

二叉树

什么是二叉树

二叉树的一些性质

二叉树的存储

二叉树的遍历

层序遍历

前序遍历

代码展示：

代码解释：

中序遍历

代码展示：

代码解释：

后序遍历

代码展示：

代码解释：

二叉树的一些简单操作

求结点个数

代码展示：

代码解释：

求叶子结点个数

代码展示：

代码解释：

求第K层节点的个数

代码展示：

代码解释：

求二叉树的高度

代码展示：

代码解释：

检测值为val的元素是否存在

代码展示：

代码解释：

层序遍历

代码展示：

代码解释：

判断是否为完全二叉树

代码展示：

代码解释：

相关文章：