数据结构——排序（万字解说）初阶数据结构完

目录

1.排序

2.实现常见的排序算法

2.1 直接插入排序

 ​编辑

2.2 希尔排序

2.3 直接选择排序

2.4 堆排序

2.5 冒泡排序

2.6 快速排序

2.6.1 递归版本

2.6.1.1 hoare版本

2.6.1.2 挖坑法

2.6.1.3 lomuto前后指针

2.6.1.4 时间复杂度

2.6.2 非递归版本

2.7 归并排序

3 性能比较

4.非比较排序

5..排序算法复杂度及稳定性分析

---

1.排序

排序就是排序，排序大家都不陌生，接下来跟作者一起进入学习吧！

常见的排序算法：

2.实现常见的排序算法

2.1 直接插入排序

直接插入排序是⼀种简单的插入排序法，其基本思想是：把待排序的记录按其关键码值的大小逐个插 入到⼀个已经排好序的有序序列中，直到所有的记录插⼊完为止，得到⼀个新的有序序列

 

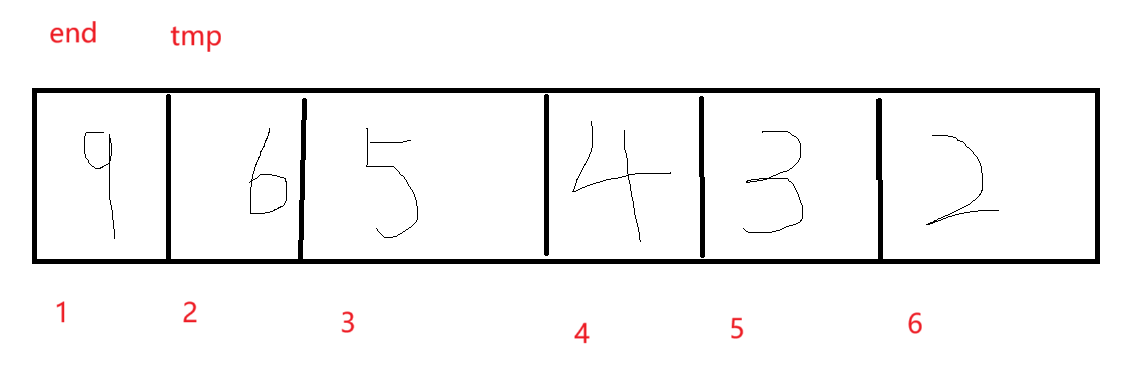
这是张图片，咱们先来看代码，然后跟着代码来分析它的思想：

void zhijiecharuSort(int* arr, int n)
{//里面挪动一大部分，外面才挪动一小部分for (int i = 0; i < n - 1; i++)//end只能到n-2，若是end到了n-1，那么tmp就越界了，无数据，无法比较了.而这个i++可以改变每次end的位置{int end = i;int tmp = arr[end + 1];while (end >= 0)//定义end的左范围，防止越界{if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;//这个时候的end是end--后的end，所以此时的end+1的值就是之前end的值}
}

假定end为有序数据的最后一位，而tmp为待排数据的第一位。上面的排的是升序。

1.先将 tmp中的值保存进tmp，即tmp=arr[end+1]。（为了防止end位置的数据存进tmp时，tmp数据被覆盖了，找不到）

2.将end与tmp进行比较，若end>tmp，则将end数据交给tmp，即arr[end+1]=arr[end]

3.end--；（继续比较前面的数据）

4.将arr[end+1]=tmp从而实现了排序

5.外部i不断地加加，内部end不断地减减，从而实现了从一开始的位置，一直到最后的位置，每个位置都有end来从这个位置一直比较到最开始的地方。

来看动图：

时间复杂度为n^2,这个是每次比较，都把数据给比较满了，即1+2+3+.....+n-1=n^2。所以最差的情况就是n^2。最好的情况就是数组有序且升序，这样话就是n个1相加，时间复杂度为n。而平均情况就是介于n^2与n之间，是小于n^2的。

所以为了接近n^2,大的数据在前，小的数据灾后。这样，越到后面，交换的次数越多。

为了接近n，小的数据在前，大的数据在后即可。

但其实，这个时间复杂度不是很好，所以咱们有一个对于它的优化版本。

2.2 希尔排序

该排序是用来优化直接插入排序的，又称为缩小增量排序。（增量，即gap）

 

gap等于几，即分成几组，且gap只是一种距离，即gap等于5时，说明分成了5组，每个组中间有gap-1个元素。如上图所示，这样的前后衔接的其实是有2大组的。并且这个排序结合了直接插入排序的2个优势：

1.增量大时，分组多，但组内元素少（一整个大组），效率高。 

2.随着增量的减少，虽然组内的元素增加，但也越来越有序，效率也越来越高。

下面看代码：（代码以gap=2为例）end与tmp每次只需要往后挪动一位即可

void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//n/3,n/3/3,n/3/3/3,最后gap只要取到1即可for (int i = 0; i < n - gap; i++)//i指向最后一个数的前一个指标所在的位置{//其实你内层不要管具体排的是哪一组，因为外层的++会让每一组都排上int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;//到这就是end-=gap了}}
}

 

时间复杂度：

外层的时间复杂度为logn。 

 内层循环：

需要注意的是，上面所说的1+2+3+...........+(n/gap-1),这个只是取值范围，并不是真正的2，3）。

还有就是可发现这个次数是呈现出先上升后下降的规律的，用图表示就是：

 

因此，希尔排序在最初和最后的排序的次数都为n，即前⼀阶段排序次数是逐渐上升的状态，当到达 某⼀顶点时，排序次数逐渐下降至n，而该顶点的计算暂时无法给出具体的计算过程 。

所以咱们给到的希尔排序的时间复杂度为n^1.3

2.3 直接选择排序

选择排序的基本思想： 每⼀次从待排序的数据元素中选出最小（或最大）的⼀个元素，存放在序列的起始位置，直到全部待 排序的数据元素排完。

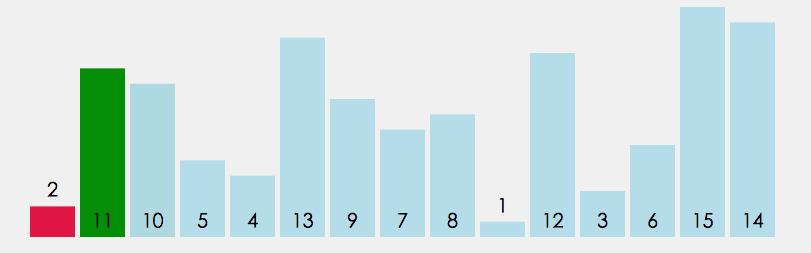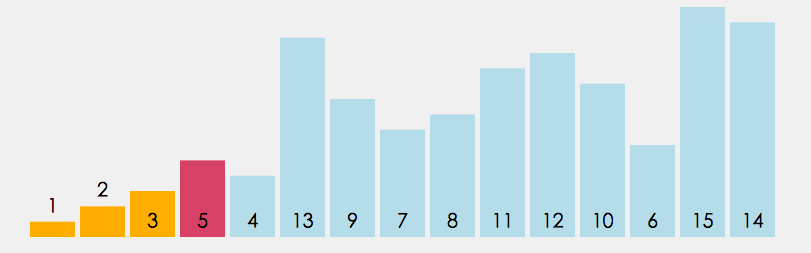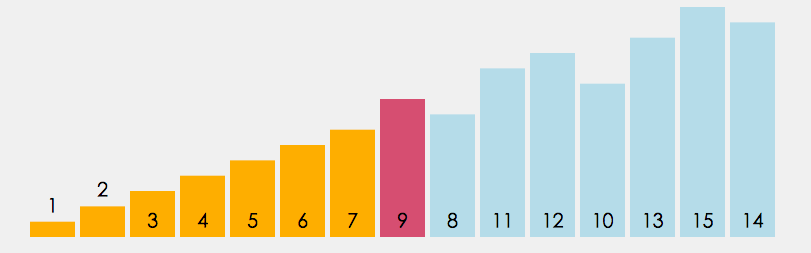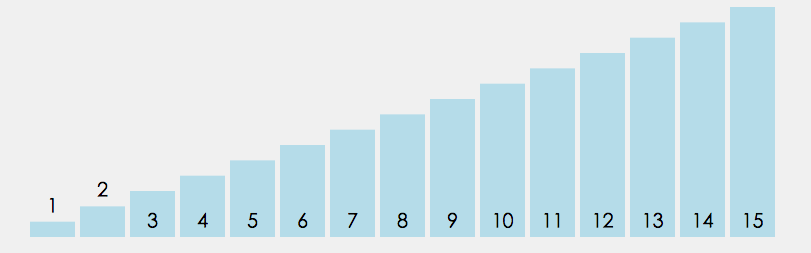 先上动图：

 这里直接选择排序我有两种写法，先来看第一种吧，我本人认为第一种是最好理解的：

void zhijieSort2(int* arr, int n)
{for (int left = 0; left < n - 1; left++) {int mini = left; // 正确初始化mini为当前leftfor (int right = left + 1; right < n; right++) {if (arr[right] < arr[mini]) {mini = right;}}Swap(&arr[mini], &arr[left]); // 直接交换到正确位置}
}

OK，咱们来看这段代码，配合者动图看。这段代码的逻辑就是 我先定义最左边的数为最小的数，之后，从左到右一次的遍历，寻找比最左侧还小的数，如果找到了，交换，交换完之后left++即可。若是没找到，说i明最左侧即最小，left也++，继续往后比较。怎么样，这段代码的逻辑是不是很简单。那么再来看第二种写法：

void zhijieSort(int* arr, int n)
{int begin = 0;int end = n - 1;//begin，end都是下标while (begin < end){int maxi = begin;int mini = begin;for (int i = begin + 1; i <= end; i++){if (arr[i] > arr[maxi]){maxi = i;}if (arr[i] < arr[mini]){mini = i;}}if (begin == maxi){maxi = mini;}Swap(&arr[mini], &arr[begin]);Swap(&arr[maxi], &arr[end]);begin++;end--;}
}

这个代码的逻辑不是那么好理解，咱们需要提前知道一个东西，就是这个方法是从左右两边同时开始排。即左边排最小，右边排最大。

咱们来看这张图并一起来看代码：就是让maxi与mini一开始都指向begin，那么之后寻找maxi与mini，

1.如果maxi==begin，那么这个时候，由于要先将 mini与begin交换，但是这样一交换之后，就会导致maxi这个地方就是mini了，那么后面的maxi与end交换，就得不到最大值了。所以咱们要先将maxi挪动到mini的位置上，这样，就算mini与begin交换，maxi（mini）的位置还是最大值，你说对吧。这就是为什么要移动maxi位置的原因。交换后，begin++，end--继续比较即可。

2.如果maxi！=begin，那么直接交换就可以了，不需要任何顾虑。

这样一看，第二种方法的逻辑还是比较难理解一些的。

时间复杂度：1.直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用

2.时间复杂度： O(N^2)

2.4 堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的⼀种排序算法，它是选择排序的⼀ 种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

这个方法，咱们在上一节中重点讲的这个方法，不记得的记得去回顾一下哦。

2.5 冒泡排序

交换排序基本思想： 所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置 交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

鱼儿吐泡泡大家都见过吧，没错，基本就是这个思想。因为每⼀个元素都可以像小气泡⼀样，根据自身大小⼀点⼀点向数组的⼀侧移动。

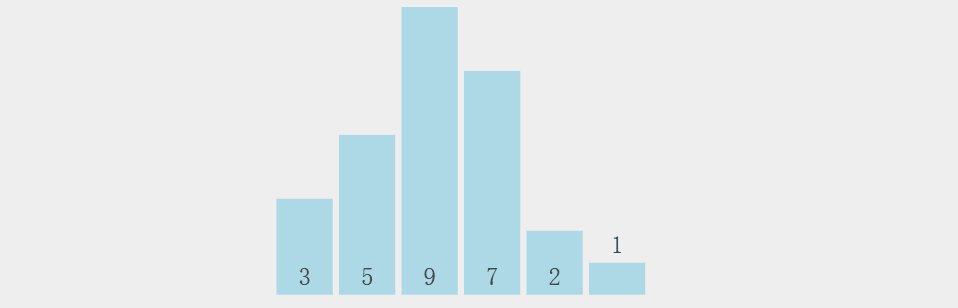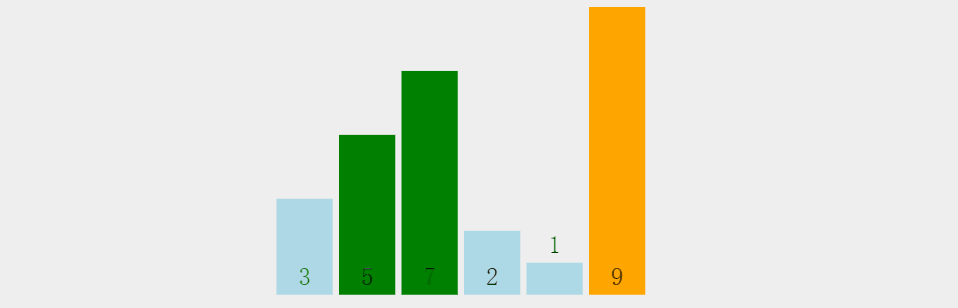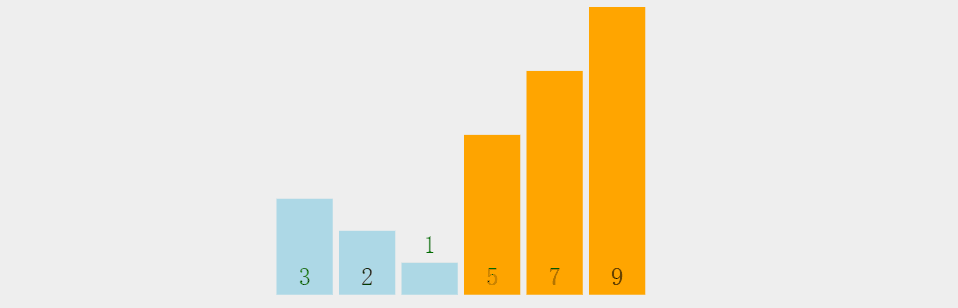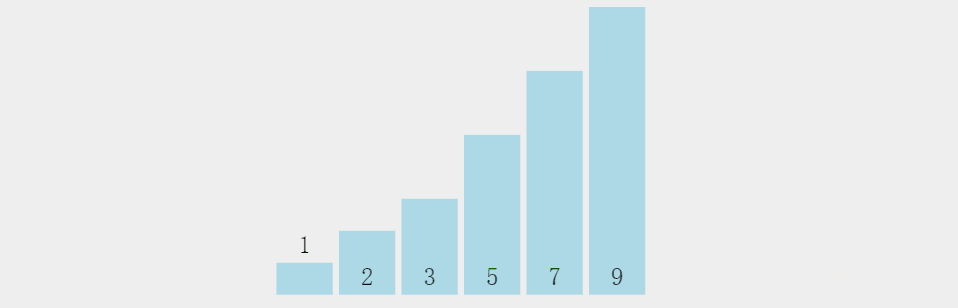
上图为动图。

void BubbleSort(int* arr, int n)
{for (int i = 0; i < n; i++){int exchange = 0;for (int j = 0; j < n - 1 - i; j++)//j<n-1-i只起到了屏障的作用，当i增加的时候，右边的屏障也在向左移动{if (arr[j] > arr[j + 1]){exchange = 1;Swap(&arr[j], &arr[j + 1]);}}}
}

 其实冒泡排序本身不是很好，所以他只起到了一个教学作用。

时间复杂度：

上面的冒泡排序的时间复杂度的分析节选自《大话数据结构》P383，由此可见，冒泡排序的时间复杂度为n^2。

2.6 快速排序

快速排序是Hoare于1962年提出的⼀种二叉树结构的交换排序方法，其基本思想为：任取待排序元素 序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小 于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列 在相应位置上为止。 

所以，快速排序就是冒泡排序的升级版本。

2.6.1 递归版本

基本框架：（需要用到递归）

void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//找基准值//int keyi = _QuickSort(arr, left, right);int keyi = _QuickSort2(arr, left, right);//left  keyi  right//左序列：[left,keyi-1]   右序列：[keyi+1,right]QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}

那么咱们目前最主要的就是寻找基准值。从而实现划分。 

寻找基准值的几种方法：

2.6.1.1 hoare版本

那么这里涉及到两个问题：

1.为什么跳出循环后right位置的值⼀定不大于key？ 

当 l eft > right 时，即right⾛到left的左侧，而left扫描过的数据均不大于key，因此right此时指 向的数据⼀定不大于key。

2.为什么left和right指定的数据和key值相等时也要交换？

相等的值参与交换确实有⼀些额外消耗。实际还有各种复杂的场景，假设数组中的数据大量重复时， 无法进行有效的分割排序。 

先来看一下代码的基本实现思路吧：

right：从右往左找比基准值小的。

left：从左往右找比基准值大的。

找到后，让left与right数据交换，后right--，left++，之后重复步骤即可。

当left>right时，停止 查找，让right与基准值进行交换，且每次找到基准值后，再次分左右（分的时候不带基准值）。

OK，下面来看代码：

int  _QuickSort(int* arr, int left, int right)//找基准值的方法之一
{int keyi = left;++left;//left++也可以吗？while (left <= right){if (left <= right && arr[right] > arr[keyi])//若是right先找到小的，则站那不动，直到等到left找到比基准值大的{++right;}if (left <= right && arr[left] < arr[keyi]){++left;}if (left <= right){Swap(&arr[left++], &arr[right++]);}}Swap(&arr[keyi], &arr[right]);return right;
}

 

原理就是这样一个原理。小的放左边，大的放右边，中间的是中等大小的。最后再排成小，中，大这样的一个即可。

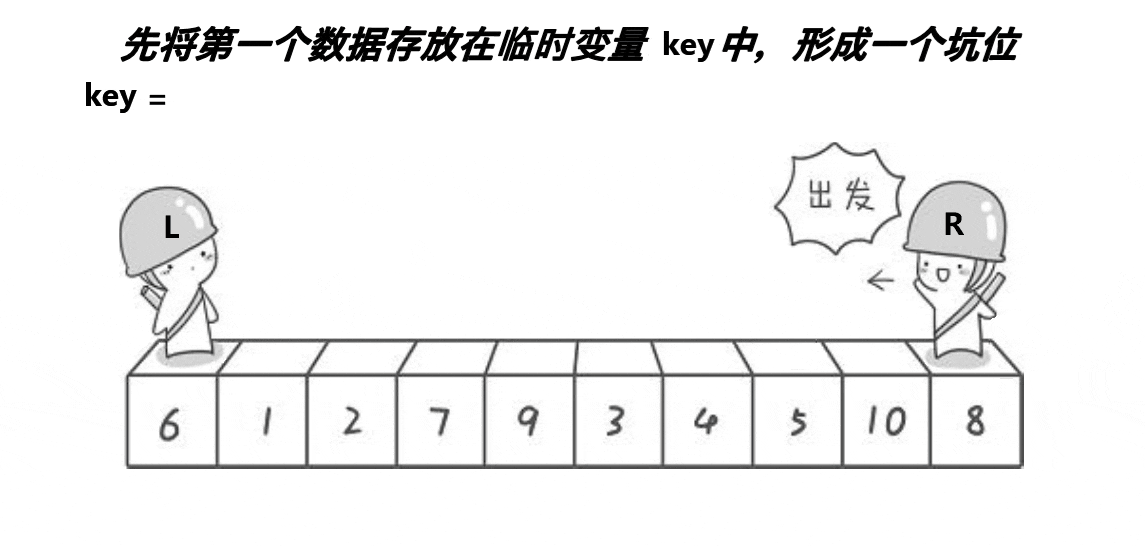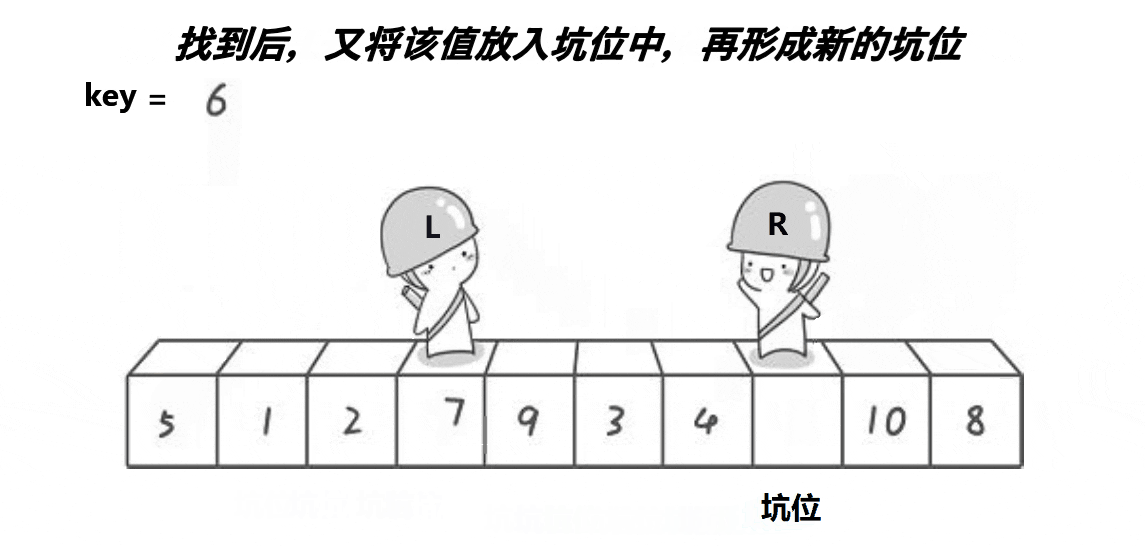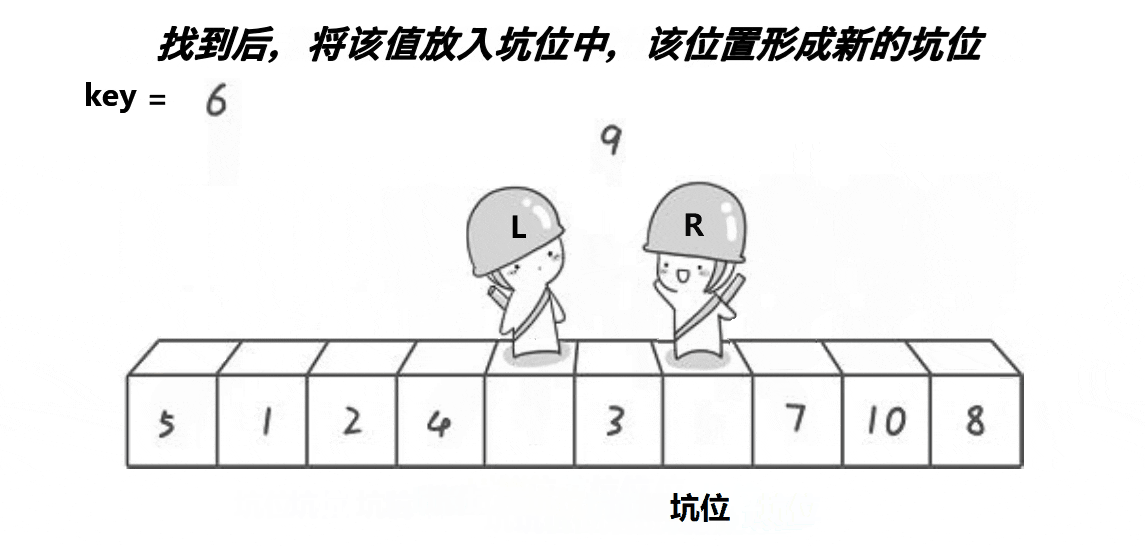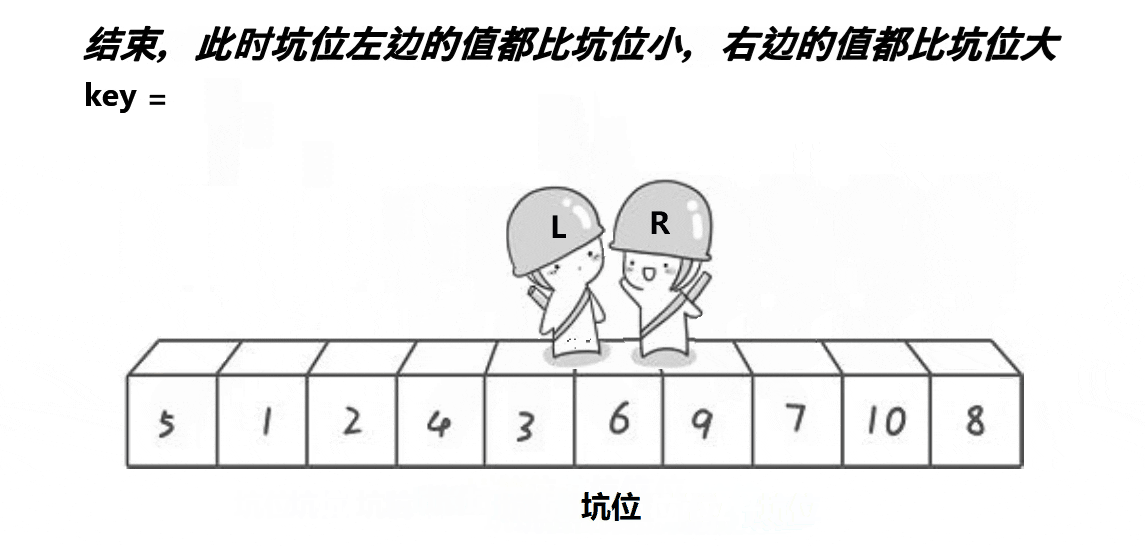
2.6.1.2 挖坑法

思路：  创建左右指针。⾸先从右向左找出比基准小的数据，找到后立即放⼊左边坑中，当前位置变为新 的"坑"，然后从左向右找出比基准大的数据，找到后⽴即放入右边坑中，当前位置变为新的"坑"，结 束循环后将最开始存储的分界值放入当前的"坑"中，返回当前"坑"下标（即分界值下标）。

来看代码：

​
int _QuickSort(int* a, int left, int right) 
{int mid = a[left];int hole = left;int key = a[hole];while (left < right){while (left < right && a[right] >= key) {--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;}​

来看这段代码的逻辑吧：

首先，代码开始部分：

int mid = a[left];

这里声明了一个变量mid，赋值为a[left]，也就是数组最左边的元素。

接下来：

int hole = left;

int key = a[hole];

这里hole被初始化为left，也就是基准值的位置，key存储了基准值的数值。这里可能是在使用“挖坑法”来进行分区操作。挖坑法的思路是将基准值的位置作为初始的“坑”，然后从右往左找比基准小的数填到左边的坑，再从左边找比基准大的数填到右边的坑，交替进行，直到左右指针相遇，最后将基准值填入最后的坑中。

然后进入循环：

while (left < right)

这个循环条件是左右指针还没有相遇，继续处理。

在循环内部，首先从右往左扫描：

while (left < right && a[right] >= key)

{--right;

}

这里，右边的指针right向左移动，直到找到一个小于key的元素。这里需要注意的是，条件中的a[right] >= key，当元素等于key时也会停止，这可能导致分区不平衡，但在某些实现中这样是可以接受的，不过可能会导致重复元素较多时的性能问题。

找到之后，将a[right]的值填入hole的位置：

a[hole] = a[right];

然后更新hole的位置为right，即当前的右指针位置：

hole = right;

接下来，从左往右扫描：

while (left < right && a[left] <= key)

{

++left;

}

这里，左指针left向右移动，直到找到一个大于key的元素。同样，a[left] <= key的条件会在遇到等于key时继续移动，这里可能需要确认是否正确，但通常这样的处理是允许的，因为等于基准值的元素可以被分到任一边。

找到之后，将a[left]的值填入当前的hole位置：

a[hole] = a[left];

然后更新hole的位置为left：

hole = left;

循环结束后，将基准值key填回到最后的hole位置：

a[hole] = key;

返回hole作为基准值的最终位置。

 

 

2.6.1.3 lomuto前后指针

创 建前后指针，从左往右找比基准值小的进行交换，使得小的都排在基准值的左边。

 

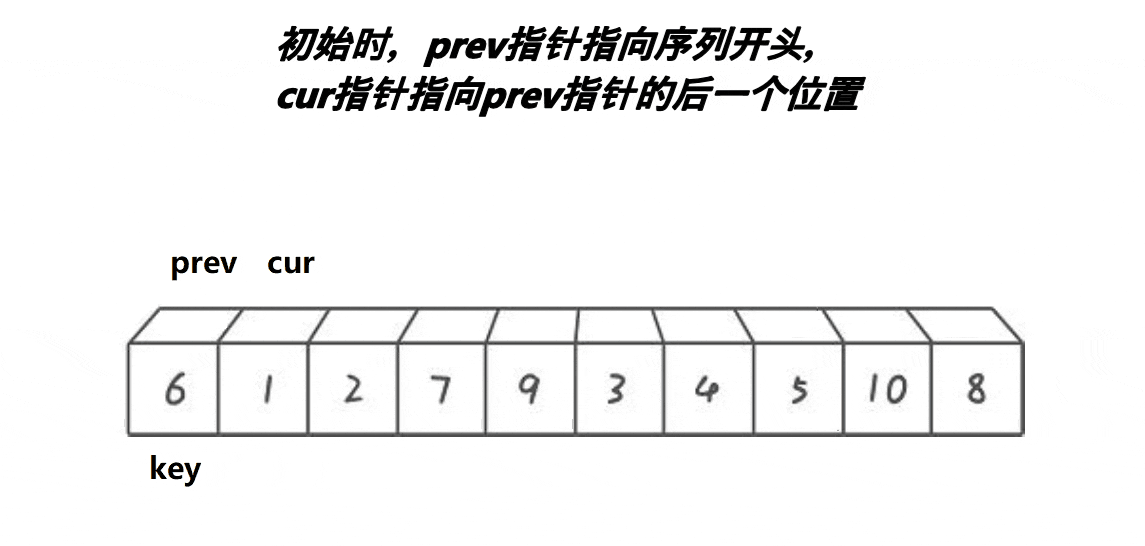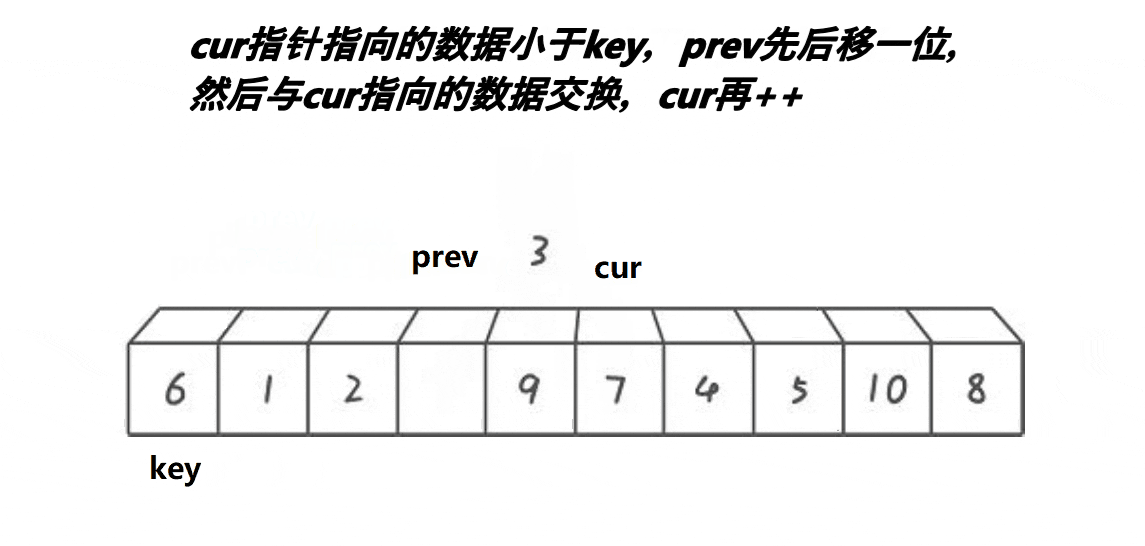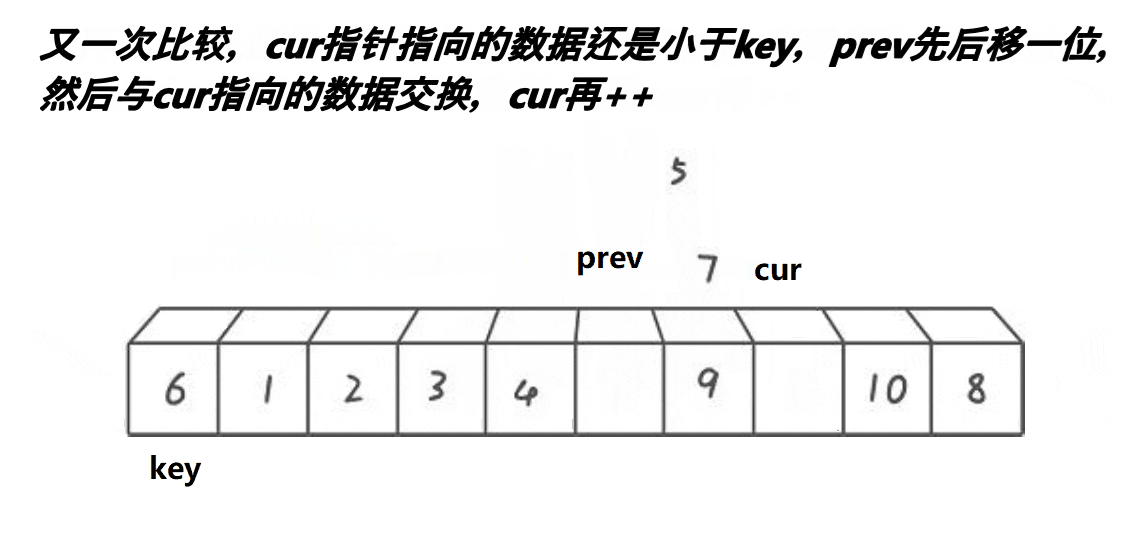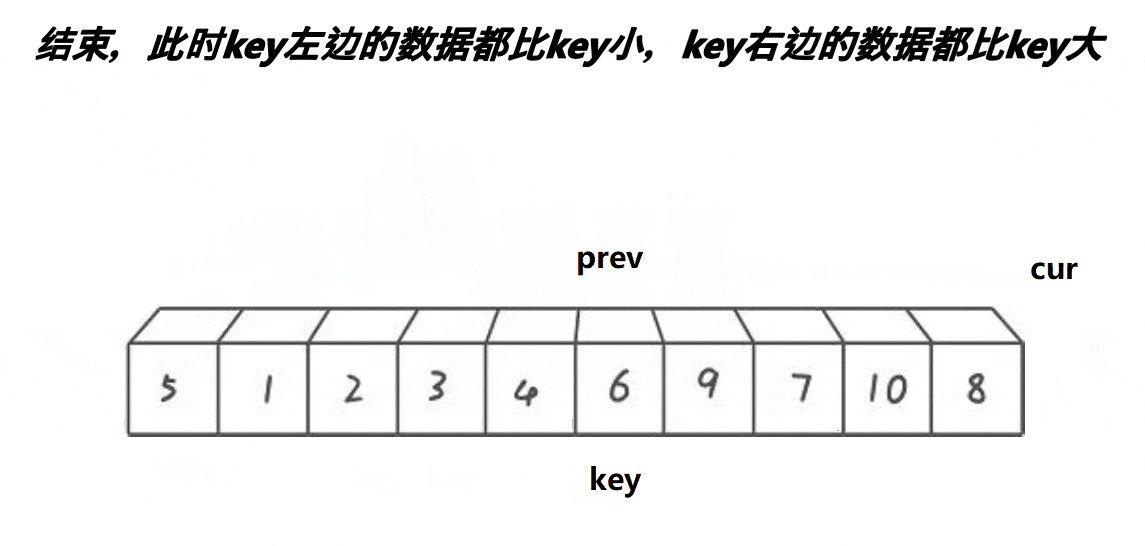
创建两个前后变量prev，cur。cur从左往右找比基准值小的数据，找到后，prev++，交换prev与cur，cur++。当cur越界后，prev与基准值交换。（这样prev左边就是小的数据了）。但是当++prev等于cur时，就不交换了，因为他俩指向同一个位置，交换了也是白交换。 

//双指针找基准值方法
//创建两个变量prev，cur，cur从前往后找比基准值小的，找到之后，先让prev++
//之后再交互prev跟cur，cur++，直到cur越界，交换prev与基准值
//这样做的话基准值左边全是比他小的
int _QuickSort1(int* arr, int left, int right,int n) //同名的函数
{int prev = left;int cur = left + 1;int keyi = left;while (cur <= right){if (arr[keyi] > arr[cur] && ++prev != cur){Swap(&arr[prev], &arr[cur]);cur++;}}Swap(&arr[keyi], &arr[prev]);return prev;
}

这里有一点需要注意，就是while循环中有一个if判断语句，这里需要说明一下：&&中若前一个条件已经被否定了，则不会执行下一个！只有前一个条件满足时，才会执行下一个条件。

2.6.1.4 时间复杂度

时间复杂度都为nlogn。

2.6.2 非递归版本

用栈进行序列的存储。可以将由基准值划分出来的这俩序列存到栈里面，然后依次取栈顶，找到对应的序列，对它进行排序。入栈，先入左序列，或先入右序列，都是可以的。

来看代码吧：

void QuickSortNonR(int* a, int left, int right){ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);//这个是让ps->top--，从而改变top的位置的int end = STTop(&st);STPop(&st);// 
单趟int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;// [begin, keyi-1] keyi [keyi+1, end] if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi-1){STPush(&st, keyi-1);STPush(&st, begin);}}STDestroy(&st);}

来看这段代码的逻辑吧：

函数内部定义了一个ST结构体的实例st，并进行了初始化。接着，将right和left依次压入栈中。然后进入一个循环，条件是栈不为空。在循环内部，首先弹出栈顶的两个元素作为begin和end，这表示当前要处理的子数组的左右边界。

接下来是单趟排序的部分。这里定义了keyi为begin，也就是当前子数组的第一个元素作为基准值。然后prev和cur初始化为begin和begin+1，这看起来像是使用了一种类似于前后指针的方法来进行分区操作。在cur循环中，当a[cur]小于基准值时，prev先自增，然后如果prev不等于cur，就交换a[prev]和a[cur]的位置。这应该是将小于基准值的元素移动到prev的位置，cur继续前进，直到遍历完整个子数组。最后，交换基准值a[keyi]和a[prev]，将基准值放到正确的位置，此时keyi更新为prev，也就是基准值的最终位置。

完成一趟排序后，代码将子数组分成两部分：[begin, keyi-1]和[keyi+1, end]。接下来，检查这两个子数组是否需要继续处理。如果keyi+1 < end，说明右边的子数组还有多个元素需要排序，于是将end和keyi+1压入栈中。同样，如果左边的子数组begin < keyi-1，则压入keyi-1和begin。这样，栈中的元素会不断分解为更小的子数组，直到所有子数组都被处理完毕。

 

2.7 归并排序

归并排序算法思想： 归并排序（MERGE-SORT）是建立在归并操作上的⼀种有效的排序算法,该算法是采用分治法（Divide andConquer）的⼀个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个 子序列有序，再使⼦序列段间有序。若将两个有序表合并成⼀个有序表，称为二路归并。 

在这咱们只实现递归版本。

 合并的时放数据时候，不要让其从下标为0开始（有的数据下标不是0，因为int index=begin），用临时的数组存储临时合并的数据。

来看代码：

//归并排序
//这个是递归，递完之后，还会再归回来，所以说这个地方left，mid等
//值都是随时随地刷新的，即每递归一次，这里的数据就会更新一次，这样的话，从小将转换成大将的
//时候，每一组小将转换成大将的时候（即是2个数据转成一个大数组），left，right，mid
//都可以确保他在最新的位置
void _mergeSort(int* arr, int left, int right, int *tmp/*这里定义临时数组的目的就是为了能够方便的存储由小将转变成大将存储的地方*/)
{if (left >= right){return;}int mid = (left + right) / 2;_mergeSort(arr, left, mid, tmp);_mergeSort(arr, mid+1, right, tmp);int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{//少了一个tmp[index++] = arr[begin2++];}}//到这时，有两种情况（不满足上面while的两种情况）//左序列数据没有全部放到tmp数组中//右序列数据没有全部放到tmp数组中while(begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//tmp中有序数据导入到原数组for (int i = left; i <= right; i++){arr[i] = tmp[i];}//这儿每递归一次时间复杂度为n
}
void mergeSort(int* arr, int left, int right, int n)
{int* tmp = (int*)malloc(n * sizeof(int));if (tmp == NULL){perror("malloc fail!");exit(1);}_mergeSort(arr, 0, n - 1, tmp);free(tmp);tmp = NULL;//这个的时间复杂度为logn（不就相当于二叉树的深度嘛）
}

来看一下这段代码中的一些东西：

 

这个就是往里面放的时候的逻辑。

还要注意的是，这个归并排序并没有开辟新的数组来存放那些小将们，还是用的原来的数组。这一点别搞错了！ 

时间复杂度：

咱们知道递归的时间复杂度计算方法为：

单词递归的时间复杂度为n ，递归次数为logn（二叉树深度），所以它的时间复杂度为O（nlogn）。

3 性能比较

那么前面的七种算法，在排序中都要进行数据的大小比较，因此这些算法也被称为比较排序算法。那么有比较，也得有非比较呀，不慌，咱们呢先来看一下性能比较：

 由此可见，堆排序与快速排序，是最好的，最快的。

4.非比较排序

计数排序：（这个最考验的其实就是下标的问题）

计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。操作步骤：

1）统计相同元素出现次数。

2）根据统计的结果将序列回收到原来的序列中。

那么为什么这么开空间呢？

首先，你使用最大值加1这个方法来进行开空间对于几个小数据有用，但是万一数据量非常大呢？就比如105，你这样开，前面的空间不全部浪费了吗？

第二种，按范围开，可以是可以，但是要注意下标，下标要灵活存储（用max-min+1确定数组的大小）。用arr[i]-min确定下标 

统计数据出现的次数，直接遍历即可。遍历时，碰到哪个后，直接++即可。即cout[arr[i]-min]++。

那个下标所在的数组++一次（即相同元素出现的次数）。

那么如何回到原来的那个数组上呢？给上cout[i](即相同元素出现的次数），然后，在原数组定义一个index，从0开始，arr[index]=i+min（这个是要存储的数）。count[i]为存储的次数。

ok,接下来请看代码：

void CountSort(int* arr, int n)
{int min = arr[0], max = arr[0];for (int i = 1; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}//max minint range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail!");}memset(count, 0, sizeof(int) * range);//直接用calloc也是可以的for (int i = 0; i < n; i++){count[arr[i] - min]++;}//将次数还原到原数组中int index = 0;for (int i = 0; i < range; i++){//数据出现的次数count[i]//下标———源数据 i+minwhile (count[i]--){arr[index++] = i + min;}}
}

来让我们分析一下这段代码，其实逻辑挺简单的：

函数开始部分，首先找出数组中的最小值min和最大值max。这一步通过遍历数组完成，初始化min和max为第一个元素，然后逐个比较更新min和max。

接下来计算range = max - min + 1，这是确定数据覆盖的范围大小。例如，如果max是5，min是0，那么range是6（0到5共6个数）。这里需要注意当数据范围较大的时候，可能会需要很大的内存，这也是计数排序的局限性之一。

然后分配一个大小为range的整数数组count，用于记录每个数出现的次数。这里用了malloc分配内存，并检查是否分配成功。之后用memset将count数组初始化为0，确保所有元素的计数从零开始。或者，用户提到可以用calloc，这样就不需要memset了，因为calloc会自动初始化为零。

接下来，遍历原数组arr，对每个元素arr[i]，计算其在count数组中的位置（arr[i] - min），并将对应的count值增加1。

最后，将统计结果还原到原数组中。这里使用一个index变量来跟踪当前要写入的位置，然后遍历count数组的每个位置i。对于每个count[i]，即元素i+min出现的次数，通过while循环将i+min写入原数组count[i]次。例如，如果count[3]是2，那么原数组中会连续放入3+min两次。

 

确实挺简单的吧。

计数排序在数据范围集中时，效率很高，但是适⽤范围及场景有限。 

时间复杂度： O(N+range)。

5..排序算法复杂度及稳定性分析

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的 相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，⽽在排序后的序列中，r[i]仍在r[j]之 前，则称这种排序算法是稳定的；否则称为不稳定的。

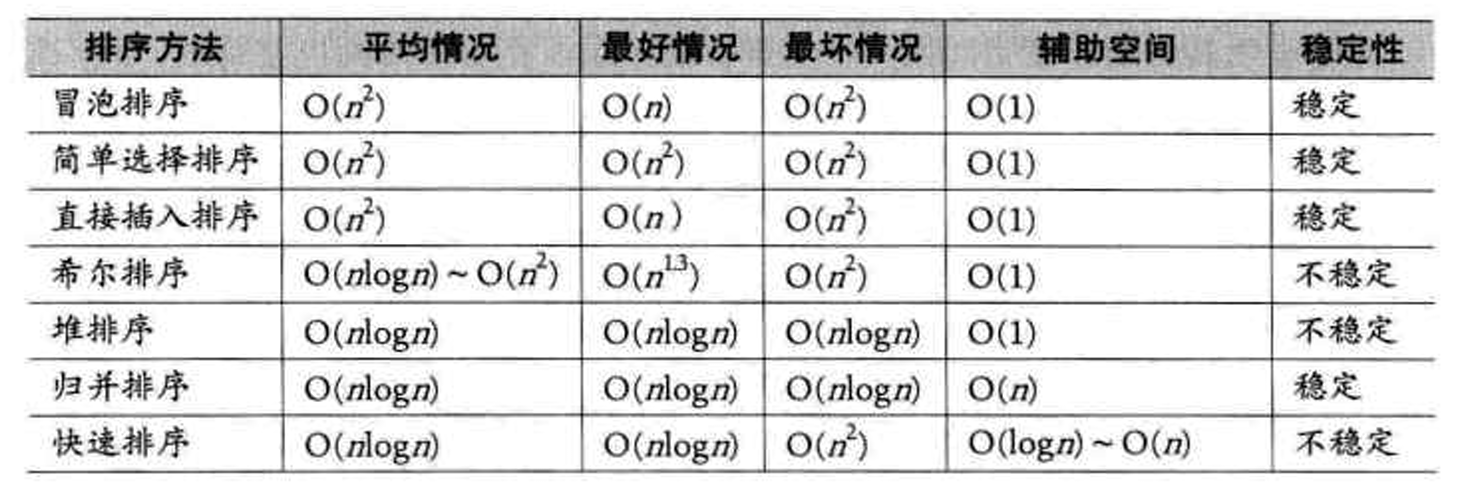上表选自《大话数据结构》P429.

 

具体的大家可以自行查看《大话数据结构》这本书，讲的相当不错。

最后看一下稳定性案例：

 

OK，到此为止，排序这一章总算是讲完了，也写了1w多字，希望大家可以好好学习一下，今天为止，初阶数据结构就讲完了，下面我会更新高新数据结构的。