当前位置：首页 > news >正文

【机器学习】Logistic 回归

news 来源：原创 2025/8/16 1:18:45

Logistic 回归虽然名字中带有“回归”，但它实际上是一种广泛应用于 二分类问题 的线性分类算法。

Logistic 回归的核心任务是预测一个样本属于正类的概率，而概率必须在 [ 0 , 1 ] 范围内。

Logistic回归通过将输入特征的线性组合映射到概率空间，输出介于 [0,1] 的概率值，通常以0.5作为阈值进行分类（ >0.5 正类；<0.5 负类）。

一、Logistic 回归的引入：为什么不用线性回归做分类？

线性回归的输出是一个连续值，形式为其值域为 ( − ∞ , + ∞ ) 。

在二分类问题中，我们通常希望预测类别标签（如0或1），或者表示样本属于某个类别的概率（范围在 [ 0 , 1 ] ）。

将线性回归直接用于分类存在以下问题：

输出范围不匹配：线性回归的输出可能远大于1或小于0，无法直接解释为概率。例如，预测值 𝑦 = 5或 𝑦 = − 3在分类中没有意义。
对离群点敏感：线性回归对离群点非常敏感，少量异常值可能显著改变模型的决策边界，导致分类性能下降。

二、Logistic回归引入

为了解决上述问题，逻辑回归被提出作为一种专门针对分类问题的算法。

逻辑回归通过以下方式改进：

概率输出：使用Sigmoid函数将线性组合映射到 [0,1]，直接输出样本属于正类的概率 P(y=1∣x)。
对数损失：采用对数损失作为目标函数，专门优化分类任务的概率预测，更加适合离散标签的场景。
非线性映射：Sigmoid函数引入非线性，使得模型能更好地适应分类任务的概率分布特性。
鲁棒性：逻辑回归通过概率建模，对离群点的敏感性较低，且决策边界更适合分类任务。

因此，逻辑回归在分类问题中取代线性回归，成为二分类任务的首选算法，同时也可通过扩展（如Softmax回归）处理多分类问题。

三、Logistic回归的数学原理

3.1 模型假设

假设输入特征为 x=[x1,x2,…,xn]，权重为 w=[w1,w2,…,wn] ，偏置为 b。

线性组合为：

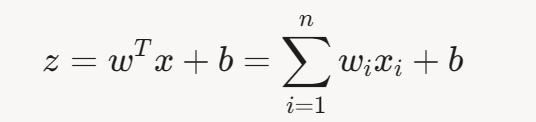
为了将 z 映射到 [ 0 , 1 ] 的概率，使用 Sigmoid函数：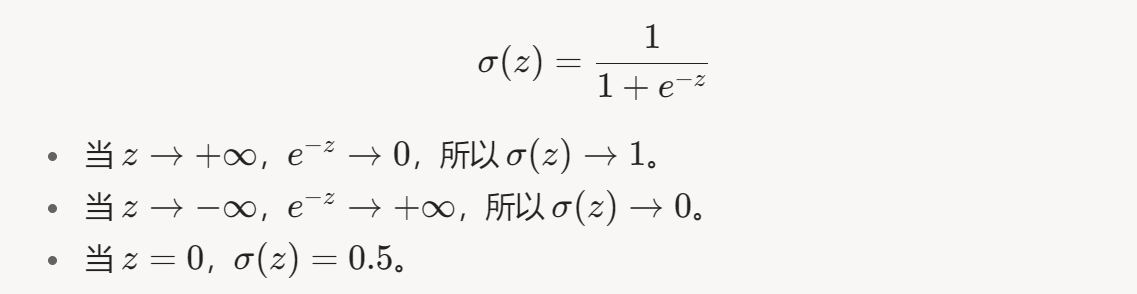

因此，样本属于正类的概率为：

y 是真实标签, P(y=1∣x) 表示给定特征 x 时，标签为正类（y=1）的概率。

负类的概率为：

3.2 决策边界

逻辑回归通过概率阈值（通常为0.5）进行分类：

若 P(y=1∣x)≥0.5 ，预测 y=1 。
若 P(y=1∣x)<0.5，预测 y=0。

当 σ(z)=0.5 时，z=0，因此决策边界为：

这表示特征空间中的一个超平面，用于分隔两个类别。

我理解的逻辑回归实现的是这样一个功能：给定一个样本，经过算法处理最终会得到一个介于0-1之间的值，而这个值实际上就表示了这个样本属于正类的概率，然后刚开始会有一个人为设定的阈值（通常是0.5），如果这个输出概率值大于阈值，那么我们就认为样本属于正类。

四、损失函数

为了训练模型，需要找到使预测最优的权重 w 和偏置 b，通过最小化损失函数实现。

4.1 对数损失

逻辑回归使用对数损失（或二元交叉熵）作为损失函数，衡量预测概率与真实标签的差异。

对于单个样本(x i ,y i )，其中 y i ∈{0,1}，预测概率为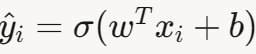

损失为：对于包含 m 个样本的数据集，总损失（平均对数损失）为：

4.2 正则化

为防止过拟合，可在损失函数中加入正则化项：

L2正则化（Ridge）

L1正则化（Lasso）

其中， λ 是正则化强度。

五、优化方法

逻辑回归通过最小化损失函数 𝐽 ( 𝑤 , 𝑏 ) 训练模型，优化参数 𝑤 和 𝑏 。

由于损失函数是非线性的，无法直接求解，因此通常使用迭代优化方法，以梯度下降为核心。

本节详细讲解梯度下降的原理、变体、收敛性等。

5.1 损失函数回顾

逻辑回归的损失函数为对数损失：

其中

目标是找到 𝑤 和 𝑏 ，使 𝐽 ( 𝑤 , 𝑏 ) 最小。

5.2 梯度下降原理

梯度下降是一种迭代优化算法，通过沿损失函数梯度的反方向更新参数，逐步逼近最小值。

更新规则为：

5.2.1 梯度推导

对于单个样本 (x i ,y i )，损失为：

其中

对 𝑤 𝑗 求偏导：

第一项：

第二项（Sigmoid 导数）：
第三项：

合并：

对 𝑏 :

对整个数据集，梯度为：

5.2.2 梯度下降步骤

初始化 w和 b ，通常为随机值或零向量。
计算预测概率。
计算梯度。
更新参数：。
重复直到损失收敛（达到最大迭代次数或损失变化小于阈值）。

5.3 梯度下降变体

梯度下降有多种实现方式，平衡计算效率和稳定性。

5.3.1 批量梯度下降（Batch Gradient Descent）

原理：每次迭代中使用 整个数据集 来计算损失函数的梯度，确保梯度方向准确。

优点：

梯度准确：使用所有样本，梯度方向稳定，收敛路径平滑。
适合小型数据集：当数据量小（数百到数千样本），计算成本可接受。

缺点：

计算成本高，内存需求大（需加载全部数据）。
更新慢：每次迭代耗时长，收敛速度慢。

5.3.2 随机梯度下降（Stochastic Gradient Descent, SGD）

原理：每次迭代中随机选择一个样本计算梯度，极大降低单次计算成本。

单样本梯度为：

参数更新规则：

优点

计算效率高：单次迭代复杂度为 O(n) O(n) O(n)，适合大型数据集。
快速更新：频繁更新参数，收敛初期进展快。
随机性有益：梯度噪声可能帮助逃离鞍点。

缺点

梯度噪声大：单样本梯度不代表整体方向，更新路径震荡，收敛不稳定。
收敛慢：接近最小值时，噪声导致难以精确收敛。

5.3.3 小批量梯度下降（Mini-Batch Gradient Descent）

原理：每次迭代使用一小批样本计算梯度

优点

效率与稳定平衡：比批量梯度下降快，比 SGD 噪声小。
适合大型数据集：分批处理，内存需求适中。
支持并行计算：批量计算可利用 GPU 加速。
收敛稳定：梯度噪声适中，收敛路径较平滑。

缺点

需调参：批量大小影响性能，需实验选择。
内存需求：比 SGD 高，需加载批量数据。
仍需调学习率：收敛依赖 α \alpha α 和批量大小。

六、Logistic回归应用实例：基于二维数据集的分类实践

6.1 背景与目标

逻辑回归是一种广泛用于二分类问题的机器学习算法。

本实例使用数据集 `Logistic_testSet.txt`（包含 100 个样本，2 个特征 ( x1 ，x2 )，标签 0 或 1），目标是训练模型、优化分类效果，并通过可视化展示决策边界和性能评估。

6.2 数据与预处理

数据集：100 个样本，特征 x1 、x2 表示二维坐标，标签0或1表示类别。

预处理：使用 `StandardScaler` 标准化特征，均值为 0，方差为 1，确保梯度下降收敛。

数据集：

-0.017612	14.053064	0
-1.395634	4.662541	1
-0.752157	6.538620	0
-1.322371	7.152853	0
0.423363	11.054677	0
0.406704	7.067335	1
0.667394	12.741452	0
-2.460150	6.866805	1
0.569411	9.548755	0
-0.026632	10.427743	0
0.850433	6.920334	1
1.347183	13.175500	0
1.176813	3.167020	1
-1.781871	9.097953	0
-0.566606	5.749003	1
0.931635	1.589505	1
-0.024205	6.151823	1
-0.036453	2.690988	1
-0.196949	0.444165	1
1.014459	5.754399	1
1.985298	3.230619	1
-1.693453	-0.557540	1
-0.576525	11.778922	0
-0.346811	-1.678730	1
-2.124484	2.672471	1
1.217916	9.597015	0
-0.733928	9.098687	0
-3.642001	-1.618087	1
0.315985	3.523953	1
1.416614	9.619232	0
-0.386323	3.989286	1
0.556921	8.294984	1
1.224863	11.587360	0
-1.347803	-2.406051	1
1.196604	4.951851	1
0.275221	9.543647	0
0.470575	9.332488	0
-1.889567	9.542662	0
-1.527893	12.150579	0
-1.185247	11.309318	0
-0.445678	3.297303	1
1.042222	6.105155	1
-0.618787	10.320986	0
1.152083	0.548467	1
0.828534	2.676045	1
-1.237728	10.549033	0
-0.683565	-2.166125	1
0.229456	5.921938	1
-0.959885	11.555336	0
0.492911	10.993324	0
0.184992	8.721488	0
-0.355715	10.325976	0
-0.397822	8.058397	0
0.824839	13.730343	0
1.507278	5.027866	1
0.099671	6.835839	1
-0.344008	10.717485	0
1.785928	7.718645	1
-0.918801	11.560217	0
-0.364009	4.747300	1
-0.841722	4.119083	1
0.490426	1.960539	1
-0.007194	9.075792	0
0.356107	12.447863	0
0.342578	12.281162	0
-0.810823	-1.466018	1
2.530777	6.476801	1
1.296683	11.607559	0
0.475487	12.040035	0
-0.783277	11.009725	0
0.074798	11.023650	0
-1.337472	0.468339	1
-0.102781	13.763651	0
-0.147324	2.874846	1
0.518389	9.887035	0
1.015399	7.571882	0
-1.658086	-0.027255	1
1.319944	2.171228	1
2.056216	5.019981	1
-0.851633	4.375691	1
-1.510047	6.061992	0
-1.076637	-3.181888	1
1.821096	10.283990	0
3.010150	8.401766	1
-1.099458	1.688274	1
-0.834872	-1.733869	1
-0.846637	3.849075	1
1.400102	12.628781	0
1.752842	5.468166	1
0.078557	0.059736	1
0.089392	-0.715300	1
1.825662	12.693808	0
0.197445	9.744638	0
0.126117	0.922311	1
-0.679797	1.220530	1
0.677983	2.556666	1
0.761349	10.693862	0
-2.168791	0.143632	1
1.388610	9.341997	0
0.317029	14.739025	0

6.3 代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, roc_curve, auc, confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split# 加载数据集
def load_data(filename):data = np.loadtxt(filename, delimiter='\t')X = data[:, :-1]y = data[:, -1].astype(int)return X, y# 决策边界绘制函数
def plot_decision_boundary(X, y, model, scaler, w, b, filename='decision_boundary_contour_only.png'):X_original = scaler.inverse_transform(X)x_min, x_max = X_original[:, 0].min() - 0.5, X_original[:, 0].max() + 0.5y_min, y_max = X_original[:, 1].min() - 0.5, X_original[:, 1].max() + 0.5xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.005), np.arange(y_min, y_max, 0.005))grid = np.c_[xx.ravel(), yy.ravel()]grid_scaled = scaler.transform(grid)Z = model.predict(grid_scaled).reshape(xx.shape)Z_prob = model.predict_proba(grid_scaled)[:, 1].reshape(xx.shape)plt.figure(figsize=(8, 6))plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Paired)plt.scatter(X_original[y == 0][:, 0], X_original[y == 0][:, 1], c='blue', label='Class 0', marker='o', s=50)plt.scatter(X_original[y == 1][:, 0], X_original[y == 1][:, 1], c='red', label='Class 1', marker='^', s=50)# 绘制 P=0.5 等高线（实线）contour = plt.contour(xx, yy, Z_prob, levels=[0.5], colors='k', linewidths=1.5)plt.clabel(contour, inline=True, fmt={0.5: 'P=0.5'}, colors='k')plt.xlabel('Feature 1 (x1)')plt.ylabel('Feature 2 (x2)')plt.title('Logistic Regression Decision Boundary')plt.legend()plt.grid(True)plt.savefig(filename, dpi=300, bbox_inches='tight')plt.show()# ROC 曲线绘制函数
def plot_roc_curve(y_true, y_scores, filename='roc_curve_final.png'):fpr, tpr, thresholds = roc_curve(y_true, y_scores)roc_auc = auc(fpr, tpr)optimal_idx = np.argmax(tpr - fpr)optimal_threshold = thresholds[optimal_idx]optimal_tpr = tpr[optimal_idx]optimal_fpr = fpr[optimal_idx]plt.figure(figsize=(8, 6))plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')plt.scatter(optimal_fpr, optimal_tpr, c='red', s=100, label=f'Optimal threshold = {optimal_threshold:.2f}')plt.xlim([0.0, 1.0])plt.ylim([0.0, 1.05])plt.xlabel('False Positive Rate')plt.ylabel('True Positive Rate')plt.title('Receiver Operating Characteristic (ROC) Curve')plt.legend(loc="lower right")plt.grid(True)plt.savefig(filename, dpi=300, bbox_inches='tight')plt.show()return roc_auc, optimal_threshold# 绘制混淆矩阵
def plot_confusion_matrix(y_true, y_pred, filename='confusion_matrix.png'):cm = confusion_matrix(y_true, y_pred)disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=['Class 0', 'Class 1'])disp.plot(cmap=plt.cm.Blues)plt.title('Confusion Matrix (Test Set)')plt.savefig(filename, dpi=300, bbox_inches='tight')plt.show()# 主程序
def main():filename = 'Logistic_testSet.txt'X, y = load_data(filename)scaler = StandardScaler()X_scaled = scaler.fit_transform(X)X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)model = LogisticRegression(solver='lbfgs', max_iter=2000, C=0.5, random_state=42)model.fit(X_train, y_train)y_pred_train = model.predict(X_train)y_pred_test = model.predict(X_test)train_accuracy = accuracy_score(y_train, y_pred_train)test_accuracy = accuracy_score(y_test, y_pred_test)print(f"训练集准确率: {train_accuracy:.4f}")print(f"测试集准确率: {test_accuracy:.4f}")print(f"权重 w: {model.coef_}")print(f"偏置 b: {model.intercept_}")y_scores = model.predict_proba(X_test)[:, 1]roc_auc, optimal_threshold = plot_roc_curve(y_test, y_scores, 'roc_curve_final.png')print(f"测试集 AUC: {roc_auc:.4f}")print(f"最优阈值: {optimal_threshold:.4f}")y_pred_optimal = (y_scores >= optimal_threshold).astype(int)optimal_accuracy = accuracy_score(y_test, y_pred_optimal)print(f"使用最优阈值的测试集准确率: {optimal_accuracy:.4f}")plot_confusion_matrix(y_test, y_pred_optimal, 'confusion_matrix.png')plot_decision_boundary(X_scaled, y, model, scaler, model.coef_, model.intercept_,'decision_boundary_contour_only.png')if __name__ == "__main__":main()

6.4 结果分析

6.4.1 决策边界

不难发现：

蓝色圆点（Class 0）和红色三角形（Class 1）分布清晰。
决策边界（黑色实线）为 P(y=1) = 0.5 等高线，基于网格点预测概率绘制。
数据近似线性可分，少量误分类点。

6.4.2 ROC 曲线

AUC = 0.97，模型性能优异

4.3 混淆矩阵（基于测试集测试结果）

七、学习总结

逻辑回归是一种用于二分类问题的机器学习算法，通过sigmoid函数将线性回归的输出映射到0到1之间，表示样本属于正类的概率。其核心是利用最大似然估计优化参数，构建损失函数（通常为对数损失），通过梯度下降等方法最小化损失来拟合模型。逻辑回归假设数据特征与目标变量之间存在线性关系，适合处理线性可分的数据。它简单高效，广泛应用于分类任务，如垃圾邮件检测、疾病预测等，但对非线性关系和多类问题需扩展处理。