概统期末复习--速成

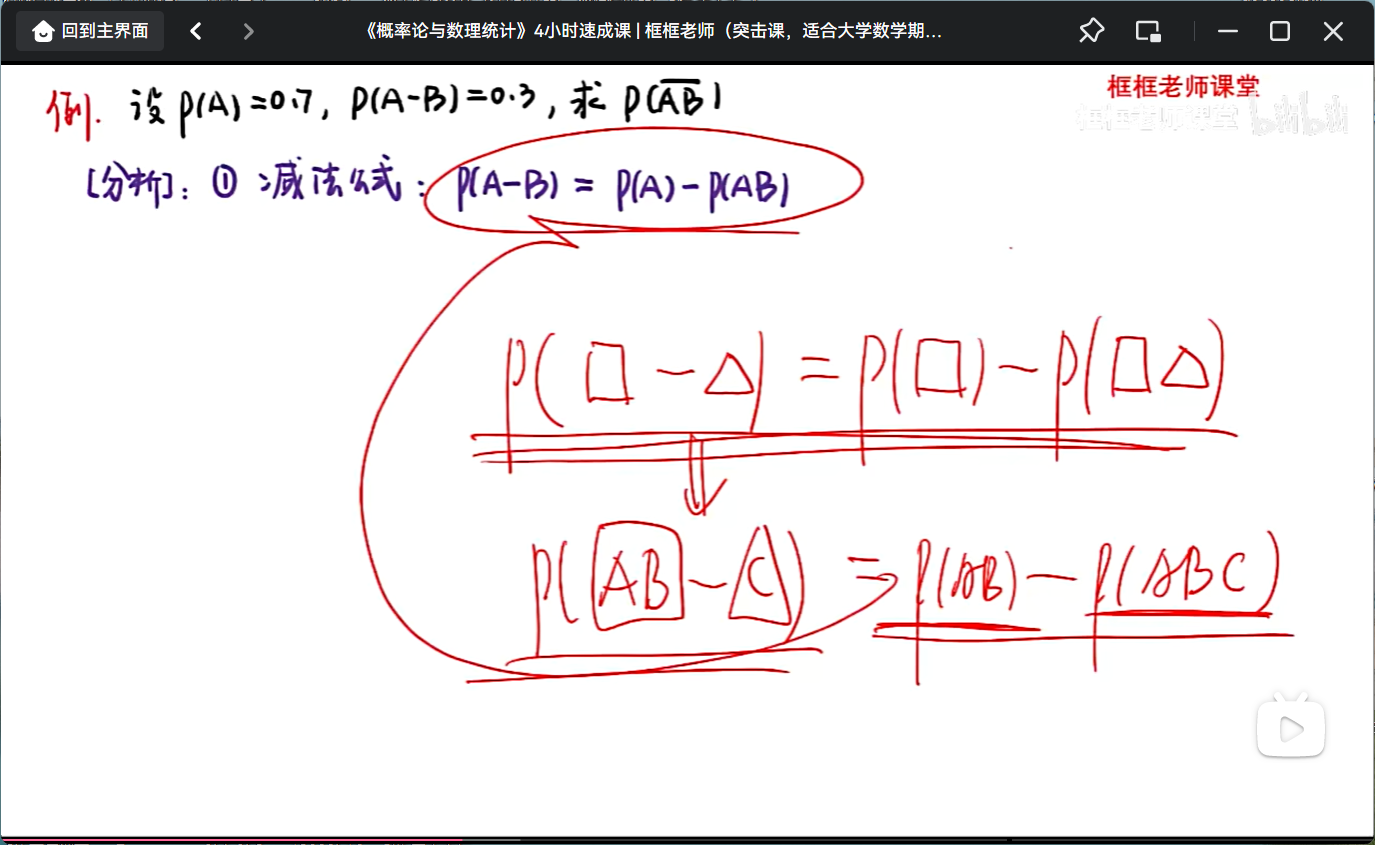
随机事件及其概率 加法公式 推三个的时候ABC，夹逼准则 减法准则 除法公式 相互独立定义 两种分析 两个解法 古典概型求概率（排列组合） 分步相乘、分类相加 全概率公式和贝叶斯公式 两阶段问题 第一个小概率*A在小概率的概率。。。累计 …...

目录 一.条件测试 1.三种测试方法 2.正整数值比较 3.字符串比较 4.逻辑测试 二.脚本中常用命令 1.echo命令 2.date命令 3.cal命令 4.tr命令 5.cut命令 6.sort命令 7.uniq命令 8.cat多行重定向 三.if语句 1.使用格式 2.if语句实例 四.case格式 1.使用格式 2…...

15.Spring Security对Actuator进行访问控制 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocati…...

#include <Eigen/Core> #include <Eigen/Dense>平移 x轴 // 原始点或对象的坐标Eigen::Vector3d original_point(1.0, 2.0, 3.0);std::cout << "original_point: " << std::endl << original_point << std::endl;// x 轴上的平…...

基站综合测试仪是通信网络建设和维护中的关键工具&#xff0c;主要用于对基站设备进行全面的性能验证和故障诊断&#xff0c;确保其符合行业标准并稳定运行。其主要作用包括&#xff1a; 1. 基站发射机性能测试 射频参数测量&#xff1a;检测发射功率、频率精度、调制质量&…...

文章目录 Android setContentView()源码分析前提setContentView() 源码分析总结 Android setContentView()源码分析 前提 Activity 的生命周期与 ActivityThread 相关&#xff0c;调用 startActivity() 时&#xff0c;会调用 ActivityThread#performLaunchActivity()&#xf…...

BERT微调 微调 BERT BERT 对每一个词元&#xff08; token &#xff09;返回抽取了上下文信息的特征向量 不同的任务使用不同的特征 句子分类 将 < cls > 对应的向量输入到全连接层分类 命名实体识别 识别一个词元是不是命名实体&#xff0c;例如人名、机构、位置…...

1、生成资源模版 使用 --dry-run 创建资源&#xff1a; kubectl create deploy web-ng --imagenginx:1.28 --replicas2 --dry-runclient -o yaml # 查询是否存在 web-ng的资源 kubectl get deployment -A |grep web-ng 通过以上命令可以看到&#xff0c;web-ng的deployment并没…...

一、硬件设计关键信息 原理图概要: 1. 核心板&#xff1a;上电时序控制&#xff0c;DDR3&#xff0c;Flash。 2. 底板&#xff1a;以太网&#xff0c;USB&#xff0c;IO&#xff0c;AD9361&#xff0c;射频链路等。 设计Xlinx的原理图和PCB设计需要的文档&#xff1a; 1、…...

以下是对长颖燕麦优化算法（AOO）的深度解析，结合其灵感来源、算法原理、公式推导及性能实测分析： 一、算法原理与行为建模 长颖燕麦优化算法（AOO）基于燕麦种子的三种自然行为设计优化策略，模拟其适应环境的动态过程： 种子传播（全局探索阶段） 行为模拟：种子通过风、水…...

一、大模型架构 了解常见的大模型架构&#xff0c;如 GPT 系列、LLaMA 系列、GLM 系列、Qwen 系列、DeepSpeek 系列等。对比他们之间的差异&#xff0c;以及每个模型演变过程 模型主要机构技术路线特点中文适配情况GPT 系列OpenAIDecoder-only对话能力强、商业化领先英文为主&a…...

BBS (cute): 1.0.2 来自 <BBS (cute): 1.0.2 ~ VulnHub> 前言&#xff1a;攻击机无法扫描靶机解决方案 1&#xff0c;在开机时&#xff0c;按下shift进入界面&#xff0c;按e进入该界面 2&#xff0c;ro替换为 rw signie init/bin/bash 3&#xff0c;按Ctrl键X键如果没成…...

面试问题列表&#xff1a; Redis支持哪些数据类型&#xff1f;各适用于什么场景&#xff1f; Redis为什么采用单线程模型&#xff1f;优势与瓶颈是什么&#xff1f; RDB和AOF持久化的区别&#xff1f;如何选择&#xff1f;混合持久化如何实现&#xff1f; Redis缓存穿透、雪…...

搭建Spark YARN模式集群步骤 1. 环境准备 系统&#xff1a;采用Linux系统&#xff08;如Ubuntu、CentOS &#xff09;&#xff0c;借助ntp实现节点间时间同步&#xff0c;关闭防火墙及SELinux。 Java&#xff1a;安装JDK 8及以上版本&#xff0c;配置JAVA_HOME环境变量。 H…...

简而言之&#xff1a;静态库是.o文件&#xff0c;是直接编译到进程里面的&#xff0c;其他的进程不能使用&#xff0c;动态库是.so文件&#xff0c;是放到linux的文件系统里面的&#xff0c;在程序运行的时候去拿来调用&#xff0c;所以多个进程都能访问 # Linux中的静态库与动…...

TVM 卷积算子注册代码深度解析 源码位置&#xff1a;src/relay/op/nn/convolution.cc 作用&#xff1a;conv2d等算子的注册实现 TVM_REGISTER_NODE_TYPE(Conv2DAttrs);TVM_REGISTER_GLOBAL("relay.op.nn._make.conv2d").set_body_typed([](Expr data, Expr weight,…...

近年来&#xff0c;全球跨境电商市场格局正经历深刻变革&#xff0c;东南亚、非洲、拉美和中东等新兴市场凭借人口红利和互联网渗透率提升&#xff0c;成为国际电商企业竞相争夺的蓝海。然而&#xff0c;在这场全球化的电商浪潮中&#xff0c;俄罗斯市场正以惊人的增速和独特的…...

HHblits 与 HHsearch 的核心区别及远源同源检测能力对比 一、核心功能与定位差异 特征HHblitsHHsearch核心目标快速迭代搜索，构建高质量多序列比对（MSA）和 Profile HMM，用于大规模序列聚类与初步同源筛选。高精度 Profile HMM-HMM 比对，用于深度同源检测与结构 / 功能预测…...

一、从 C 到 C 1、引用&#xff08;掌握&#xff09; 1.1 概念 别名机制&#xff1a;引用本质上是对变量的一种别名&#xff0c;它就像变量的另一个名字&#xff0c;对引用的操作实际上就是对原变量的操作。从底层实现来看&#xff0c;引用可能是通过指针来实现的&#xff0…...

本地构建module模块的AAR gradle.properties isCommonApp false模块的build.gradle apply plugin: com.android.library&#xff1a;module模块编译manifest.srcFile src/main/AndroidManifest.xml&#xff1a;读取没有启动App和Activity的配置文件 if (isCommonApp.toBoo…...

从中国地区通过 wsl --install 或 Microsoft Store 安装 WSL 发行版&#xff08;如 Ubuntu&#xff09;时&#xff0c;下载速度往往非常慢&#xff0c;甚至卡在 0% 很久。这是因为微软服务器在国内访问速度受限。 以下是几种 解决方法&#xff0c;可加快 WSL 发行版&#xff0…...

目录 1. 标准帧&#xff08;Standard Frame&#xff09; 2. 扩展帧&#xff08;Extended Frame&#xff09; 3. 核心区别 4. 如何区分标准帧与扩展帧&#xff1f; 5. 应用场景 6. 注意事项 在CAN&#xff08;Controller Area Network&#xff09;总线协议中&#xff0c;标…...

Coze Coze是字节跳动旗下的产品，更注重用户友好性和C端场景优化。其主要特点包括： ‌快速部署‌：Coze提供拖拽式界面和丰富的插件（如天气查询、电商导流工具），适合快速搭建对话机器人和轻量化应用‌。‌生态集成‌：Coze依托字节生态，支持与飞书、抖音等平台的无缝集成…...

初始状态 假设当前从根节点 b 开始&#xff0c;此时栈为空 。 第一步&#xff1a;处理根节点 b 的左子树 调用 goAlongLeftBranch 函数&#xff0c;从节点 b 开始&#xff0c;因为 b 有左子树&#xff08;节点 a &#xff09;&#xff0c;将 b 入栈&#xff0c;此时栈&#…...

前言 点到直线&#xff0c;点到面的距离公式的手工推导。很久没有数学推导了&#xff0c;再试一把。 一、初步推导 二、转换为标准的形式 三、两种特殊情况的验证 四、推广到3维的情况 结束语 可能从向量的角度来推导&#xff0c;更加的便捷。很多数学知识都忘记了&#xff0c;…...

代码随想录算法训练营第九天 |【字符串】151.翻转字符串里的单词、卡码网55.右旋转字符串、28.实现strStr、459.重复的子字符串 151.翻转字符串里的单词 思路 我的想法是模拟&#xff0c;用状态机拾取单词&#xff0c;然后存到双重数组中&#xff0c;再反向读取输出状态机有…...

文章目录 3D数学公共计算结构体Mathf常用成员三角函数 向量Vector3基本成员点乘叉乘插值运算 四元数引出基本概念Quaternion结构体成员四元数运算 更多的Mono延迟函数协同程序多线程相关协程概念辨析协程本体协程调度器 Resources资源动态加载特殊文件夹Resources同步加载Resou…...

1、根据官方文档下载tp8.1.2. php>8,tp8的运行界面已经不是初心不改了。而是值得托付。 composer create-project topthink/think tp8swoole cd tp8swoole composer require topthink/think-swoole 2、下载thinkswoole captcha,image,migration,queue,不要要template和v…...

目录 Okhttp有什么不好&#xff1f;bulid的过程create方法ServiceMethodcall enqueue的过程为什么要学习源码呢&#xff1f; 一、Okhttp有什么不好&#xff1f; Okhttp本身来说&#xff0c;是一个挺好的网络框架&#xff0c;但&#xff0c;对于开发者而言&#xff0c;使用起…...

引言&#xff1a;由于当前的 PetaLinux 系统使用了临时的内存文件系统&#xff08;initramfs&#xff09;&#xff0c;导致每次重启后所有更改&#xff08;包括安装的 EPICS&#xff09;都会丢失。为了解决这个问题&#xff0c;您需要将根文件系统&#xff08;rootfs&#xff0…...

前言&#xff1a;在前面我有文章介绍了关于单片机的SPI外设CUBEMX配置&#xff0c;但是要想使用好SPI这个外设我们还必须对其原理性的时序有一个详细的了解&#xff0c;所以这篇文章就补充一下SPI比较偏向底层的时序性的逻辑。 1&#xff0c;SPI简介 SPI是MCU最常见的对外通信…...

目录 一.priority_queue的介绍 二.仿函数 1.仿函数的介绍 2.仿函数的特点 3.实现两个简单的仿函数 三.priority_queue的接口实现 1.成员变量 2.push 3.pop 4.top 5.size 6.empty 7.构造函数 四.代码总览 priority_queue.h test.cpp 一.priority_queue的介绍 源…...

在军事演习室、应急指挥中心或城市规划馆中&#xff0c;传统沙盘曾是不可或缺的工具。然而&#xff0c;随着数字化浪潮席卷&#xff0c;“纸上谈兵”式的静态模型已无法满足现代指挥对实时性、交互性、立体化的需求。智能交互电子沙盘系统应运而生&#xff0c;它融合了GIS地理信…...

1、从官网现在安装包 上述是商业版&#xff0c;免费版如下&#xff0c;有两种可以选择&#xff0c;分别是Linux x64 和 LinuxARM64 . 然后在线安装即可&#xff0c;和Windows系统安装步骤一样。...

在当今的互联网内容生态中&#xff0c;视频已成为重要的信息传播载体。Hls&#xff08;HTTP Live Streaming&#xff09;和 Flv&#xff08;Flash Video&#xff09;作为广泛使用的视频传输协议&#xff0c;分别在移动端和 Web 端有着出色的表现。对于使用 Vue 框架进行开发的项…...

javascript:void(0) 是一个常见的 JavaScript 伪协议&#xff0c;下面从几个方面详细解释其含义和用途。 基本含义 javascript: 是一种伪协议&#xff0c;它告诉浏览器后面跟随的是一段 JavaScript 代码。void 是 JavaScript 中的一个操作符&#xff0c;void(0) 的作用是对给…...

suna目前的agent执行可视化界面主要有个实时界面&#xff0c;一个是前面介绍的浏览器访问界面&#xff0c;分析参考&#xff1a;suna工具调用可视化界面实现原理分析&#xff08;二&#xff09;-CSDN博客 下面的Terminal界面&#xff0c;对应的分析参考&#xff1a; 前端知识-…...

一、监督学习&#xff1a;老师带学生的模式 ‌核心机制‌&#xff1a;模型像学生一样&#xff0c;通过“带答案的习题”&#xff08;即带标签的数据集&#xff09;学习规律。例如&#xff0c;给模型看1000张标有“猫”“狗”的图片&#xff0c;让它学会区分两者的特征24。 ‌典…...

精益数据分析&#xff08;43/126&#xff09;&#xff1a;媒体网站商业模式的盈利与指标解析 在创业和数据分析的学习旅程中&#xff0c;我们不断探索各种商业模式的奥秘&#xff0c;今天让我们一同深入《精益数据分析》&#xff0c;聚焦媒体网站商业模式&#xff0c;剖析其盈…...

什么是图&#xff08;Graph&#xff09;&#xff1f; 在数学和计算机科学中&#xff0c;图 (Graph) 是一种抽象数据结构&#xff0c;用于表示对象之间的成对关系。一个图通常定义为一个有序对 G (V, E)&#xff0c;其中&#xff1a; V 是 顶点 (Vertices) 或 节点 (Nodes) 的…...

文章目录 引言一、Web 架构基础概念客户端 - 服务器模型HTTP 协议 二、常见 Web 架构模式单体架构微服务架构 三、Web 架构常见问题及解决方法性能问题安全问题 四、Web 架构思维导图五、总结 引言 在当今数字化的时代&#xff0c;Web 应用无处不在。无论是社交媒体平台、电子商…...

题目 思路 这道题其实也挺容易看出来是最小生成树的。我当时做的时候确实是能看出来是考的最小生成树&#xff0c;union()&#xff0c;find()那些方法我也能写出来&#xff0c;但是&#xff0c;我完全不知道怎么去利用给你的输入数据&#xff0c;去求解题目&#xff0c;也就是知…...

今天我们继续回溯算法章节&#xff0c;昨天我们重点讲的是组合问题&#xff0c;我们完美使用递归三部曲以及递归回溯相结合的方法来解决&#xff0c;当然昨天最有难度的还是去重操作&#xff0c;那个大家要多思考一下&#xff0c;那么今天我们就继续探讨回溯算法。 第一题对应…...

通过跳板机连接远程服务器时&#xff0c;报错---过程尝试写入的管道不存在 过程尝试写入的管道不存在报错解决报错内容解决方法1. 测试网络连接连接是否正常2. 检查跳板机并打开权限3. 通过跳板机登录到目标服务器4.配置文件范例 注&#xff1a;校外连接学校内网服务器报错 过程…...

C - 仿 RabbitMQ 实现消息队列&#xff08;1&#xff09;&#xff08;环境搭建&#xff09; 什么是消息队列核心特点核心组件工作原理常见消息队列实现应用场景优缺点 项目配置开发环境技术选型 更换软件源安装一些工具安装epel 软件源安装 lrzsz 传输工具安装git安装 cmake安装…...

1.BLIP的原理? BLIP是一种统一视觉语言理解和生成的预训练模型。BLIP的特点在于它采用了一种编码器-解码器混合架构&#xff08;MED)&#xff0c;并且引入了CapFilt机制来提高数据质量和模型性能。BLIP的主要组成部分包括&#xff1a; MED架构&#xff1a;包括单模态编码器、…...

Kubernetes入门 一、容器技术二、Kubernetes介绍1. Kubernetes核心资源2. Kubernetes集群架构2.1 Master2.2 Node 一、容器技术 随着技术发展&#xff0c;应用程序的部署经历了从物理机到虚拟机&#xff0c;再到容器的转变。 物理机&#xff1a;物理机会运行多个程序&#xf…...

【coze】&#xff08;售前售后问题、搜索引擎去广告&#xff09; 1、创建意图识别工作流&#xff08;1&#xff09;创建工作流&#xff08;2&#xff09;添加意图识别节点&#xff08;3&#xff09;配置意图识别节点&#xff08;4&#xff09;运行看效果&#xff08;5&#xff…...

在 Web 应用开发中&#xff0c;抽奖功能是提升用户参与度的常用手段。使用 Vue3 结合 canvas 技术&#xff0c;我们可以轻松实现一个高度自定义的抽奖转盘组件&#xff0c;不仅能设定中奖概率&#xff0c;还能灵活配置奖项图标和名称。本文将详细介绍该组件的实现原理、步骤&am…...

vue3viteAI大模型实现谷歌插件-web诊断 一、前言二、实现思路1、功模块构图2、数据交互图 三、技术栈简介1、Web端2、服务端 四、主要功能实现1、Web端【1】谷歌插件vue全局配置文件【2】加载web诊断工具至当前页面【3】全局捕获异常错误 2、Server端【1】websock管理模块【2】…...