当前位置：首页 > news >正文

#基础Machine Learning 算法（上）

news 来源：原创 2025/8/23 19:09:39

机器学习算法的分类

机器学习算法大致可以分为三类：

监督学习算法 (Supervised Algorithms）:在监督学习训练过程中，可以由训练数据集学到或建立一个模式（函数 / learning model），并依此模式推测新的实例。该算法要求特定的输入/输出，首先需要决定使用哪种数据作为范例。例如，文字识别应用中一个手写的字符，或一行手写文字。主要算法包括神经网络、支持向量机、最近邻居法、朴素贝叶斯法、决策树等。
无监督学习算法 (Unsupervised Algorithms):这类算法没有特定的目标输出，算法将数据集分为不同的组。
强化学习算法 (Reinforcement Algorithms):强化学习普适性强，主要基于决策进行训练，算法根据输出结果（决策）的成功或错误来训练自己，通过大量经验训练优化后的算法将能够给出较好的预测。类似有机体在环境给予的奖励或惩罚的刺激下，逐步形成对刺激的预期，产生能获得最大利益的习惯性行为。在运筹学和控制论的语境下，强化学习被称作“近似动态规划”（approximate dynamic programming，ADP）。

特点	监督学习	无监督学习
数据特性	数据带有标签或期望输出	数据无标签
学习目标	学习输入输出映射关系，用于预测未知数据的输出（如分类或回归）	发现数据的内在结构和模式（如聚类、降维等）
学习过程	利用标记数据进行训练，模型通过比较预测输出和真实标签来调整参数	无标记数据，模型直接分析数据特征，发现模式和结构
常见算法	分类算法：决策树、支持向量机、朴素贝叶斯等；回归算法：线性回归、岭回归等	聚类算法：k - 均值、层次聚类等；降维算法：主成分分析（PCA）、线性判别分析（LDA）等
应用场景	分类任务：垃圾邮件识别、图像分类等；回归任务：房价预测、股票价格预测等	聚类任务：客户细分、文档聚类等；降维任务：数据可视化、特征工程等

监督学习算法

线性回归算法（Linear Regression）：用于回归任务，通过拟合一条直线或超平面来预测连续值。
支持向量机算法（Support Vector Machine, SVM）：用于分类任务，通过找到一个超平面来最大化不同类别之间的间隔。
最近邻居/k-近邻算法（K-Nearest Neighbors, KNN）：用于分类和回归任务，通过查找训练集中最近的邻居来预测新样本的标签。
逻辑回归算法（Logistic Regression）：用于分类任务，通过 logistic 函数将线性回归的输出映射到概率值。
决策树算法（Decision Tree）：用于分类和回归任务，通过构建树形结构来进行决策。
随机森林算法（Random Forest）：用于分类和回归任务，是一种集成学习方法，通过构建多个决策树并综合它们的结果来进行预测。
朴素贝叶斯算法（Naive Bayes）：用于分类任务，基于贝叶斯定理，并假设特征之间相互独立。

无监督学习算法

k-平均算法（K-Means）：用于聚类任务，将数据集划分为 k 个簇，每个簇由其均值表示。
降维算法（Dimensional Reduction）：包括主成分分析（PCA）、t-SNE 等，用于减少数据的特征维度，常用于数据可视化和特征工程。

1. 线性回归算法 Linear Regression

回归分析（Regression Analysis）是统计学的数据分析方法，目的在于了解两个或多个变量间是否相关、相关方向与强度，并建立数学模型以便观察特定变量来预测其它变量的变化情况。

线性回归算法（Linear Regression）的建模过程就是使用数据点来寻找最佳拟合线。公式，y = mx + c，其中 y 是因变量，x 是自变量，利用给定的数据集求 m 和 c 的值。
线性回归又分为两种类型，即 简单线性回归（simple linear regression)，只有 1 个自变量；*多变量回归（multiple regression)，至少两组以上自变量。

公式

线性回归的公式通常表示为：
$\ y = m \cdot x + c \$
其中：

( y ) 是因变量（我们想要预测的值）。
( x ) 是自变量（用于预测 ( y ) 的值）。
( m ) 是斜率，表示 ( x ) 变化一个单位时 ( y ) 的变化量。
( c ) 是截距，表示当 ( x = 0 ) 时 ( y ) 的值。

在多变量线性回归中，公式可以扩展为：
$\ y = m_1 \cdot x_1 + m_2 \cdot x_2 + \ldots + m_n \cdot x_n + c \$
其中
$\ x_1, x_2, \ldots, x_n \$
是多个自变量，
$\ m_1, m_2, \ldots, m_n \$
是对应的系数。

例子

假设有如下数据集，描述了房屋面积（平方米）与房价（万元）之间的关系：

房屋面积（( x )）	房价（( y )）
50	60
70	80
90	100
110	120
130	140

我们想找到一条直线来描述房屋面积和房价之间的关系，以便预测新房屋的房价。

简单线性回归

在这个例子中，我们只有一个自变量（房屋面积），因此使用简单线性回归。

计算平均值：
- $\ \bar{x} = \frac{50 + 70 + 90 + 110 + 130}{5} = 90 \$
- $\\bar{y} = \frac{60 + 80 + 100 + 120 + 140}{5} = 100 \$
计算斜率（( m )）：
$\ m = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2} \$
代入数据：
$\ m = \frac{(50-90)(60-100) + (70-90)(80-100) + (90-90)(100-100) + (110-90)(120-100) + (130-90)(140-100)}{(50-90)^2 + (70-90)^2 + (90-90)^2 + (110-90)^2 + (130-90)^2} \$
计算分子和分母：
- 分子：
  $\ (-40)(-40) + (-20)(-20) + (0)(0) + (20)(20) + (40)(40) = 1600 + 400 + 0 + 400 + 1600 = 4000 \$
- 分母：
  $KaTeX parse error: Can't use function '\(' in math mode at position 2: \̲(̲-40)^2 + (-20)^…$
- 斜率：
  $\ m = \frac{4000}{4000} = 1 \$
计算截距（( c )）：
$\ c = \bar{y} - m \cdot \bar{x} = 100 - 1 \cdot 90 = 10 \$
回归方程：
$\ y = 1 \cdot x + 10 \$

预测

现在，我们可以使用这个方程来预测新房屋的房价。例如，如果房屋面积是 100 平方米，预测的房价为：
$\ y = 1 \cdot 100 + 10 = 110 \text{ 万元} \$

多变量线性回归

如果数据集中包含多个自变量，例如房屋面积和房间数量，我们使用多变量线性回归：

房屋面积（( x_1 )）	房间数量（( x_2 )）	房价（( y )）
50	2	60
70	3	80
90	4	100
110	5	120
130	6	140

建立模型：
$\ y = m_1 \cdot x_1 + m_2 \cdot x_2 + c \$
使用线性回归算法（如梯度下降或最小二乘法）来求解 ( m_1 )、( m_2 ) 和 ( c )。
预测：使用求得的参数来预测新房屋的房价。

通过这个简单的例子，可以看出线性回归如何通过拟合数据点来建立预测模型。

2. 支持向量机算法(Support Vector Machine,SVM)

支持向量机（SVM）是一种用于分类任务的监督学习算法。它的基本思想是将数据点映射到高维空间中，并找到一个最优的超平面来分隔不同类别的数据点。这个超平面的选择不仅要正确分类训练数据，还要最大化与最近数据点（支持向量）之间的距离，以提高模型的泛化能力。需要注意的是，支持向量机需要对输入数据进行完全标记，仅直接适用于二分类任务，应用将多类任务需要减少到几个二元问题。

举例说明

假设有如下数据集，描述了两类不同类别的点，用 x 和 y 表示两个特征：

表格

复制

x	y	类别
1	2	A
2	3	A
3	3	A
6	7	B
7	8	B
8	9	B

我们的目标是找到一个超平面来分隔类别 A 和类别 B。

线性可分情况

数据可视化：
- 将数据点绘制在二维平面上，类别 A 的点分布在左边，类别 B 的点分布在右边。
寻找最优超平面：
- SVM 会找到一个超平面，使得这个超平面与最近的类别 A 和类别 B 的点之间的距离最大化。
- 假设找到的最优超平面方程为：
  
  w1x+w2y+b=0
- 支持向量是那些离超平面最近的点，例如类别 A 中的点 (3, 3) 和类别 B 中的点 (6, 7)。
间隔计算：
- 计算支持向量到超平面的距离，并最大化这个距离。
分类决策：
- 对于新的数据点，根据其在超平面的哪一侧来判断其类别。

非线性可分情况

假设数据集如下，描述了两类不同类别的点，但这些点在二维空间中无法用一条直线分隔：

表格

复制

x	y	类别
1	1	A
2	2	A
3	3	A
2	4	B
3	5	B
4	6	B

数据可视化：
- 将数据点绘制在二维平面上，类别 A 的点分布在左下角，类别 B 的点分布在右上角，但无法用一条直线分隔。
核技巧：
- 使用径向基函数核（RBF）将数据映射到高维空间中，使其在高维空间中线性可分。
- RBF 核函数定义为：
  
  K(x,x′)=exp(−γ∥x−x′∥2)
  
  其中，γ 是核函数的参数，控制映射到高维空间的程度。
寻找最优超平面：
- 在高维空间中找到一个超平面来分隔数据点。
- 支持向量是那些离超平面最近的点。
分类决策：
- 对于新的数据点，将其映射到高维空间后，根据其在超平面的哪一侧来判断其类别。

3. 最近邻居/k-近邻算法 (K-Nearest Neighbors,KNN)

KNN算法是一种基于实例的学习，或者是局部近似和将所有计算推迟到分类之后的惰性学习。用最近的邻居（k）来预测未知数据点。k 值是预测精度的一个关键因素，无论是分类还是回归，衡量邻居的权重都非常有用，较近邻居的权重比较远邻居的权重大。

KNN 算法的缺点是对数据的局部结构非常敏感。计算量大，需要对数据进行规范化处理，使每个数据点都在相同的范围。

KNN 也可以用于回归问题。例如，我们有一组房屋，的数据包括房屋的面积、房龄等特征以及房价（目标变量）。当我们想要预测一套新房子的价格时，就找到训练集中与新房子在面积和房龄等方面最相似的 k 个房子，然后取这 k 个房子价格的平均值作为新房子的预测价格。不过，回归问题中的 KNN 实现细节和应用场景相对分类问题有所不同，主要在于输出结果是从连续值中预测而不是分类标签。

4. 逻辑回归算法 Logistic Regression

逻辑回归是一种用于解决二分类问题的监督学习算法（也可以通过一些扩展方法用于多分类）。它的目标是找到一个决策边界，将不同类别的数据点分开。例如，在一个二维平面上，这可能是一条直线或曲线，用于区分两类样本。

逻辑回归算法（Logistic Regression）一般用于需要明确输出的场景，如某些事件的发生（预测是否会发生降雨）。通常，逻辑回归使用某种函数将概率值压缩到某一特定范围。

逻辑回归模型的输出是一个概率值，表示样本属于某个类别的概率。这个概率值通过逻辑函数（也称为 sigmoid 函数）来计算。逻辑函数的数学表达式为：

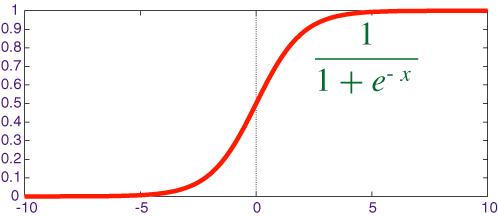
其中 z 是线性组合（如 z=θ0+θ1x1+θ2x2+⋯+θnx**n）。

在这里插入图片描述

5.决策树算法 Decision Tree

决策树（Decision tree）是一种特殊的树结构，由一个决策图和可能的结果（例如成本和风险）组成，用来辅助决策。机器学习中，决策树是一个预测模型，树中每个节点表示某个对象，而每个分叉路径则代表某个可能的属性值，而每个叶节点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，通常该算法用于解决分类问题。

一个决策树包含三种类型的节点：

决策节点：通常用矩形框来表示
机会节点：通常用圆圈来表示
终结点：通常用三角形来表示

简单决策树算法案例，确定人群中谁喜欢使用信用卡。考虑人群的年龄和婚姻状况，如果年龄在30岁或是已婚，人们更倾向于选择信用卡，反之则更少。
通过确定合适的属性来定义更多的类别，可以进一步扩展此决策树。在这个例子中，如果一个人结婚了，他超过30岁，他们更有可能拥有信用卡（100% 偏好）。测试数据用于生成决策树。

总结

算法名称	基本原理	优点	缺点	适用场景
线性回归	通过拟合一条直线或多维超平面来预测连续值。	简单易懂，计算高效。	只能处理线性关系，对异常值敏感。	回归任务，如房价预测。
支持向量机(SVM)	在高维空间中寻找一个最优超平面来分隔不同类别的数据点。	分类效果好，泛化能力强。	对参数选择敏感，计算复杂度高。	分类任务，尤其是高维数据。
K-近邻(KNN)	基于最近的邻居来预测未知数据点的类别或值。	简单易懂，适用于非线性数据。	计算量大，对数据局部结构敏感。	分类和回归任务。
逻辑回归	通过逻辑函数将线性回归的输出映射到概率值，用于二分类问题。	模型可解释性强。	假设特征独立，可能不适用于强相关特征数据。	二分类任务，如垃圾邮件识别。
决策树	通过构建树形结构来进行决策，每个节点表示某个属性的测试。	模型可解释性强，能处理非线性关系。	容易过拟合，对数据波动敏感。	分类任务，如客户细分。