当前位置：首页 > news >正文

高等数学第三章---微分中值定理与导数的应用（§3.6 函数图像的描绘§3.7 曲率）

news 来源：原创 2025/7/14 18:55:21

§3.6 函数图像的描绘

一、曲线的渐近线

对于某些函数，其图形向无穷远处延伸时，会越来越趋近于某一条直线，这条直线被称为曲线的渐近线 (Asymptote)。

1. 定义

若曲线 $y = f (x)$ 上一点 $P (x, y)$ 沿曲线趋于无穷远时，该点 $P$ 与某一直线 $L$ 的距离趋于 0，则称直线 $L$ 为曲线 $y = f (x)$ 的渐近线。
在这里插入图片描述

2. 渐近线的求法

(1) 斜渐近线 (Oblique Asymptote)

假设直线 $L : y = k x + b$ 是曲线 $y = f (x)$ 的渐近线。我们需要确定常数 $k$ 和 $b$ 。
根据点到直线的距离公式，点 $P (x, f (x))$ 到直线 $L$ 的距离为：
$\frac{|f(x) - (kx + b)|}{\sqrt{1 + k^2}}$
由渐近线的定义可知，当点 $P$ 沿曲线趋于无穷远（即 $\to \infty$ 或 $\to -\infty$ ）时，距离 $\to 0$ 。由于 $\sqrt{1+k^2}$ 是一个非零常数，这等价于：
$\lim_{x \to \pm\infty} [f(x) - (kx + b)] = 0$
由此可以推导出 $k$ 和 $b$ 的计算公式：

求 $k$ :
上式两边同除以 $x$ （假设 $\neq 0$ ）：
$\lim_{x \to \pm\infty} \left[ \frac{f(x)}{x} - k - \frac{b}{x} \right] = 0$
由于当 $\to \pm\infty$ 时， $\frac{b}{x} \to 0$ ，因此得到：
$\boxed{k = \lim_{x \to \pm\infty} \frac{f(x)}{x}}$
如果这个极限存在且有限，则计算下一步。
求 $b$ :
由 $\lim_{x \to \pm\infty} [f(x) - kx - b] = 0$ 可得：
$\boxed{b = \lim_{x \to \pm\infty} [f(x) - kx]}$
将第一步求得的 $k$ 代入此式，如果这个极限存在且有限，则直线 $y = k x + b$ 就是曲线的斜渐近线（或水平渐近线）。

注意: $\to +\infty$ 和 $\to -\infty$ 的极限可能不同，需要分别计算，可能得到不同的渐近线。

(2) 水平渐近线 (Horizontal Asymptote)

当斜渐近线的斜率 $k = 0$ 时，其方程为 $y = b$ 。此时，计算 $b$ 的公式变为：
$\lim_{x \to \pm\infty} [f(x) - 0 \cdot x] = \lim_{x \to \pm\infty} f(x)$
因此，若极限 $\lim_{x \to \pm\infty} f(x) = b$ 存在且有限，则直线 $y = b$ 是曲线的水平渐近线。这是斜渐近线的特例。

(3) 垂直渐近线 (Vertical Asymptote)

如果在某点 $x = x_0$ 附近，函数值趋于无穷大，即：
$\lim_{x \to x_0} f(x) = \infty \quad (\text{或} -\infty)$
或者单侧极限
$\lim_{x \to x_0^+} f(x) = \infty \quad (\text{或} -\infty) \quad \text{或} \quad \lim_{x \to x_0^-} f(x) = \infty \quad (\text{或} -\infty)$
成立，则直线 $x = x_0$ 是曲线的垂直渐近线。
通常在函数定义域的边界点或使分母为零的点寻找垂直渐近线。

示例

例 1： 求 $\frac{x^3}{x^2 + 1}$ 的渐近线。
(解：待补充)

例 2： 求 $\frac{x^2 + x}{x^2 - 1}$ 的渐近线。
(解：待补充)

例 3： 求 $\frac{1}{x} + \ln(1 + e^x)$ 的渐近线。
(解：待补充)

二、函数图形的作法

描绘函数 $y = f (x)$ 图形的大致步骤如下：

确定定义域: 求出使函数表达式有意义的自变量 $x$ 的取值范围。
考察对称性与周期性:
- 奇偶性: 判断 $f (- x)$ 与 $f (x)$ 的关系。若 $f (- x) = f (x)$ ，则为偶函数，图形关于 $y$ 轴对称；若 $f (- x) = - f (x)$ ，则为奇函数，图形关于原点对称。
- 周期性: 判断是否存在常数 $T > 0$ 使得 $f (x + T) = f (x)$ 对定义域内所有 $x$ 成立。若存在，则只需分析一个周期长度的区间。
研究单调性与极值:
- 计算一阶导数 $f^{'} (x)$ 。
- 求出 $f^{'} (x) = 0$ 的点（驻点）和 $f^{'} (x)$ 不存在的点（可能是极值点）。
- 用这些点划分定义域，列表分析 $f^{'} (x)$ 的符号，确定函数的单调递增和递减区间。
- 根据一阶导数在驻点或不可导点两侧的符号变化，判断并计算极大值和极小值。
研究凹凸性与拐点:
- 计算二阶导数 $f^{''} (x)$ 。
- 求出 $f^{''} (x) = 0$ 的点和 $f^{''} (x)$ 不存在的点。
- 用这些点划分定义域，列表分析 $f^{''} (x)$ 的符号，确定曲线的凹区间（ $f^{''} > 0$ ，Concave Up）和凸区间（ $f^{''} < 0$ ，Concave Down）。
- 判断凹凸性发生变化的连续点，计算拐点坐标。
确定渐近线: 按照前面介绍的方法，求出函数的水平渐近线、垂直渐近线和斜渐近线。
确定特殊点的坐标: 计算一些关键点的坐标，例如：
- 与坐标轴的交点（令 $x = 0$ 求 $y$ 截距，令 $y = 0$ 求 $x$ 截距）。
- 极值点、拐点。
描绘图形: 综合以上信息（定义域、对称性、周期性、单调区间、极值、凹凸区间、拐点、渐近线、特殊点），描绘出函数图形的草图。

示例

例 4： 作 $\frac{4(x + 1)}{x^2} - 2$ 的图形。
(解：待补充)

§3.7 曲率

一、曲率的概念

曲率 (Curvature): 描述曲线弯曲程度的量。直观地说，曲线越弯曲，曲率越大；直线或接近直线的部分，曲率越小（直线曲率为0）。
与曲率有关的量:
考察曲线上某点附近的弯曲程度，可以考虑一小段弧。
- (1) 切线转动角度的大小: 在相同弧长上，切线方向变化的角度越大，曲线弯曲程度越大。如下图示意，弧 $M_1 M_2$ 较平缓，切线转角 $\Delta\alpha_1$ 较小；弧 $M_2 M_3$ 较弯曲，切线转角 $\Delta\alpha_2$ 较大。
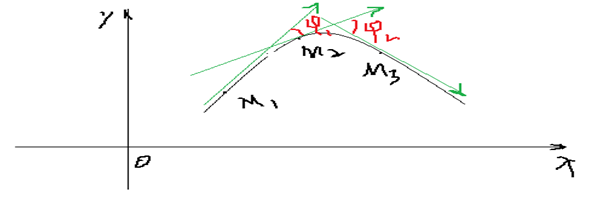
- (2) 曲线的弧长大小: 曲线的弧长越小，曲线的弯曲程度越大。如图，弧 $M_{1}M_{2}$ 与弧 $N_{1}N_{2}$ 切线转角相同，但弯曲程度不一样，显然，弧长小的弯曲程度大。
结论: 曲线的弯曲程度与切线转动角度成正比，与曲线弧长成反比。

二、曲率计算

1. 弧微分 (Arc Differential)

在这里插入图片描述

设曲线 $y = f (x)$ 在 $(a, b)$ 内具有连续导数 $f^{'} (x)$ (保证曲线光滑且弧长可积)。
考虑曲线上点 $(x, y)$ 到邻近点 $(x+\Delta x, y+\Delta y)$ 的一小段弧长 $\Delta s$ 。当 $\Delta x$ 很小时，弧长 $\Delta s$ 可以用弦长 $\sqrt{(\Delta x)^2 + (\Delta y)^2}$ 来近似。
$\Delta s \approx \sqrt{(\Delta x)^2 + (\Delta y)^2} = \sqrt{1 + \left(\frac{\Delta y}{\Delta x}\right)^2} |\Delta x|$
当 $\Delta x \to 0$ 时， $\frac{\Delta y}{\Delta x} \to y'$ 。取其微分形式，得到弧微分 $d s$ :
$\boxed{ds = \sqrt{1 + (y')^2} dx} \quad (\text{假设 } dx > 0)$
或写成对称形式： $ds^2 = dx^2 + dy^2$ 。弧微分 $d s$ 代表了弧长 $s$ 的微小改变量。

2. 曲率计算公式

在这里插入图片描述

设曲线上一点 $M$ 处的切线与 $x$ 轴正向的夹角为 $\alpha$ 。当点从 $M$ 移动到邻近点 $M^{'}$ 时，弧长变化了 $\Delta s$ ，切线转角变化了 $\Delta \alpha$ 。
定义弧 $M M^{'}$ 上的平均曲率 $\bar{k}$ 为：
$\bar{k} = \left| \frac{\Delta \alpha}{\Delta s} \right|$
表示单位弧长上切线转角的平均变化率。
当点 $\to M$ （即 $\Delta s \to 0$ ）时，平均曲率的极限即为点 $M$ 处的曲率 $k$ ：
$\boxed{k = \lim_{\Delta s \to 0} \left| \frac{\Delta \alpha}{\Delta s} \right| = \left| \frac{d\alpha}{ds} \right|}$

现在推导用 $y^{'}, y^{''}$ 表示的曲率公式：
已知切线的斜率 $\tan \alpha = y'$ 。两边对 $x$ 求导：
$\frac{d}{dx}(\tan \alpha) = \frac{d}{dx}(y')$
$\sec^2 \alpha \frac{d\alpha}{dx} = y''$
$\tan^2 \alpha) \frac{d\alpha}{dx} = y''$
$(y')^2) \frac{d\alpha}{dx} = y''$
所以 $\frac{d\alpha}{dx} = \frac{y''}{1 + (y')^2}$ 。
根据链式法则 $\frac{d\alpha}{ds} = \frac{d\alpha/dx}{ds/dx}$ ，以及 $\sqrt{1+(y')^2}$ ，可得：
$\frac{d\alpha}{ds} = \frac{ \frac{y''}{1 + (y')^2} }{ \sqrt{1 + (y')^2} } = \frac{y''}{(1 + (y')^2)^{3/2}}$
代入曲率定义 $\left| \frac{d\alpha}{ds} \right|$ ，得到直角坐标系下的曲率公式：
$\boxed{k = \frac{|y''|}{(1 + (y')^2)^{3/2}}}$

注：
若曲线由参数方程给出：
$\begin{cases} x = x(t) \\ y = y(t) \end{cases}$
则曲率公式为：
$\boxed{k = \frac{|x'y'' - x''y'|}{(x'^2 + y'^2)^{3/2}}}$
其中 $x^{'}, y^{'}$ 表示对参数 $t$ 的一阶导数， $x^{''}, y^{''}$ 表示对参数 $t$ 的二阶导数。

示例

例 1： 计算双曲线 $x y = 1$ 在点 $(1, 1)$ 处的曲率。
(解：待补充)

例 2： 抛物线 $y = ax^2 + bx + c$ ( $\neq 0$ ) 上哪一点的曲率最大？
(解：待补充)

例 3： 设圆的参数方程为
$\begin{cases} x = R \cos t \\ y = R \sin t \end{cases}$
求圆上任意点处的曲率。
(解：待补充)

三、曲率圆与曲率半径

在这里插入图片描述

设曲线 $y = f (x)$ 在点 $M$ 处的曲率为 $k$ ( $\neq 0$ )。
在点 $M$ 处的法线上，在曲线凹的一侧取点 $D$ ，使得线段 $D M$ 的长度为 $\rho = \frac{1}{k}$ 。
以 $D$ 为圆心， $\rho$ 为半径作圆。这个圆称为曲线在点 $M$ 处的曲率圆 (Circle of Curvature)。其半径 $\rho = \frac{1}{k}$ 称为曲线在点 $M$ 处的曲率半径 (Radius of Curvature)。

曲率圆在点 $M$ 处与原曲线具有相同的切线、相同的曲率，并且在点 $M$ 附近与原曲线吻合得最好（二阶接触）。曲率半径 $\rho$ 直观地表示了在该点附近最能近似曲线的圆的半径。曲率越大，曲率半径越小，表示曲线弯曲得越厉害。

§3.6 函数图像的描绘

一、曲线的渐近线

1. 定义

2. 渐近线的求法

(1) 斜渐近线 (Oblique Asymptote)

(2) 水平渐近线 (Horizontal Asymptote)

(3) 垂直渐近线 (Vertical Asymptote)

示例

二、函数图形的作法

示例

§3.7 曲率

一、曲率的概念

二、曲率计算

1. 弧微分 (Arc Differential)

2. 曲率计算公式

示例

三、曲率圆与曲率半径

相关文章：