当前位置：首页 > news >正文

WGDI-分析WGD及祖先核型演化的集成工具-文献精读126

news 来源：原创 2025/7/15 16:13:19

WGDI: A user-friendly toolkit for evolutionary analyses of whole-genome duplications and ancestral karyotypes

WGDI：一款面向全基因组重复事件与祖先核型演化分析的易用工具集

摘要

在地球上大多数主要生物类群中，人们已检测到全基因组复制（WGD）及其后续的核型变化。为了在基因组分析中更清晰地揭示这些复杂的多层次共线性模式，迫切需要便捷而精确的分析工具。为满足这一需求，我们开发了WGDI（Whole-Genome Duplication Integrated analysis，全基因组复制综合分析工具），这是一个基于Python的命令行工具，可用于全面分析多次多倍化事件及跨物种的基因组比对。

WGDI支持三种主要分析流程：多倍体推断、基因组同源性的层级推断以及祖先染色体核型分析。它能够基于高质量染色体水平的基因组数据，更有效地检测WGD事件，并深入解析与WGD相关的演化过程。值得一提的是，WGDI能提取完整的共线性区块，并助力详细核型进化的重建。

该工具包已在GitHub上免费开放获取（GitHub - SunPengChuan/wgdi: WGDI: A user-friendly toolkit for evolutionary analyses of whole-genome duplications and ancestral karyotypes）。作为应用示例，WGDI成功揭示了Aquilegia coerulea（蓝耧斗菜）与Vitis vinifera（葡萄）在经历WGD之后的核型进化过程，并否定了蓝耧斗菜是核心双子叶植物异源多倍化起源的亲本之一这一假说。

引言

已有确凿证据表明，全基因组复制（WGD）或多倍化，以及伴随而来的核型变化，在多种真核生物谱系中反复发生（Van de Peer 等，2017）。WGD 被认为是一种重要的进化过程，尤其在植物中尤为显著（Soltis 和 Soltis，2016；Landis 等，2018）。因此，识别WGD事件、确定其发生的时间与在进化史中的位置，以及重建祖先核型，对于深入理解真核生物如何多样化及适应不同环境至关重要（Fawcett 等，2009；Mabry 等，2020）。

目前，用于检测WGD的主要方法分为三类：基于同义替代速率（Ks-based）、基因树（gene tree-based）和共线性（synteny-based）的方法（Rabier 等，2014；Mabry 等，2020）。不同方法在不同数据集中的表现各有优劣（Kellis 等，2004；Hahn，2007；Vanneste 等，2013；Ruprecht 等，2017；Tiley 等，2018；Nakatani 和 McLysaght，2019；Zwaenepoel 等，2019；Zwaenepoel 和 Van de Peer，2019）。

随着越来越多高质量染色体水平基因组的组装发布，研究人员已开发出多种方法用于识别保留在染色体上的同源基因所形成的保守共线性区块。早期的方法如 ADHoRe（Vandepoele 等，2002）和 DiagHunter（Cannon 等，2003），通常依赖于相邻匹配基因对的聚类。相比之下，更新的方法使用动态规划算法来构建成对共线基因链，如 ColinearScan（Wang 等，2006）、Cyntenator（Rödelsperger 和 Dieterich，2010）、MCscan、MCScanX 和 JCVI（Tang 等，2017）。然而，鉴于频繁发生的递归WGD以及随后的基因组重组（通常伴随染色体重排和大量基因丢失）使现存基因组高度复杂，这些方法在进行所有详细后续分析方面的能力仍存在差异、不完善且耗时，具体包括生成共线基因或区块的同源性散点图或环图、Ks值计算、Ks峰拟合、祖先核型演化探索以及共线基因比较等任务（Ruprecht 等，2017；Van de Peer 等，2017；Wang 等，2018）。

为促进基于高质量染色体水平基因组的WGD分析，我们开发了一个基于Python的命令行工具包——WGDI（Whole-Genome Duplication Integrated analysis，全基因组复制综合分析）。WGDI整合了当前多数WGD相关的生物信息学分析功能，包括基因组内外的散点图比对、共线性检测、Ks估算与峰拟合、祖先核型演化研究及共线树推断。WGDI 在重建祖先核型、提取现存物种相应前体染色体方面表现出色，能够加速WGD相关核型研究的进展。

结果

WGDI软件包的结构

WGDI的完整源代码可在GitHub（GitHub - SunPengChuan/wgdi: WGDI: A user-friendly toolkit for evolutionary analyses of whole-genome duplications and ancestral karyotypes）上免费获取，并可在Windows、Linux或macOS操作系统中部署。WGDI使用Python3编写，可通过pip或conda进行安装。它包含多个子程序，用户只需修改配置文件并输入子程序名称（例如：“wgdi -d your.conf”）即可执行相应功能。WGDI的子程序参数和功能如图1A所示。WGDI支持三大主要工作流程（见图1B）： (1) 利用同源点图、共线性和Ks分布以及同源基因树进行多倍化分析与推断； (2) 针对递归古多倍化事件进行基因组同源关系的分层推断； (3) 进行亚基因组和祖先染色体核型分析及进化情景推断。 WGDI的输出可以包括矢量图（如SVG格式），适合直接用于发表（见图1C）。详细的功能说明和参数设置可参考：Usage — WGDI 0.71 documentation。

图1. WGDI软件包结构，展示主要组成部分及其依赖关系

(A) WGDI的多种用法以及各子程序之间的关联关系。 (B) WGDI的三大主要工作流程及其对应的子程序。 (C) WGDI可视化输出示例图。更多输出示例可直接访问：Welcome to WGDI’s Documentation! — WGDI 0.71 documentation。

更灵敏且更准确的共线性检测

为了评估算法性能，我们将WGDI提取的共线区与另外两款常用工具——MCScanX和JCVI（v1.2.7）提取的结果进行了对比。三款工具使用相同的数据集进行测试，即人类（Homo sapiens）与黑猩猩（Pan troglodytes）基因组。WGDI的参数设置为：repeat_number = 10，mg = 25,25，muplite = 1，grading = 50,40,25，score = 100；MCScanX和JCVI使用默认参数。在H. sapiens第12号染色体与P. troglodytes第13号染色体之间，WGDI、MCScanX和JCVI提取的共线区数量均为三个，但在同源块上提取的同源基因对数量存在显著差异（见图2A）。WGDI提取的共线基因数量多于其他两款工具，尽管JCVI的表现优于MCScanX。为了进一步探究这种差异的原因，我们以一个富集了重复基因的共线区为例，展示了三款软件的表现（见图2B）。同源基因对在该区域内以点的形式展示，使用同源点图的规则进行上色，共线基因对被放大并排列。WGDI、MCScanX和JCVI分别提取了49、28和40对同源基因。MCScanX忽略了这些重复基因富集区域，导致提取的同源基因对数量最少。此外，MCScanX和JCVI提取的共线区中漏掉了一些点，甚至包括一些（用红色标记，黑色箭头指示）没有重复基因的基因对。由于在共线性分析前进行了筛选，MCScanX和JCVI未能提取这些同源基因对。最终，WGDI和JCVI（默认参数）分别保留了61,117对和18,644对同源基因对。WGDI在同源矩阵中保留了更多的同源基因对，这有助于识别更长且更多的共线区。

图2. WGDI、MCScanX与JCVI在共线性区段提取方面的性能比较

(A) 使用WGDI、MCScanX和JCVI在人类第12号染色体与黑猩猩第13号染色体之间识别局部共线性区段。三种方法提取的共线性区段中同源基因对的数量存在显著差异。

(B) 在富含重复基因的区域提取局部共线性区段时，不同方法提取结果差异显著。图中以点状表示同源基因对，放大并对齐的为共线性基因对。WGDI根据同源性将同源基因对划分为红色、蓝色和灰色三类。图中黑色与灰色箭头所示位置代表被遗漏的红点，即应被识别为共线性基因对但未被识别。

更高灵敏度的共线性检测方法能够保留更多同源基因对，从而提升共线性区段识别的准确性。WGDI对每个基因的同源基因对进行排序与打分，并依据颜色分类的点设定不同的搜索范围，以此提高共线性区段的稳定性与精度（图3A）。对于一个给定的基因，仅当其同源基因对满足设定条件时，才被纳入共线性区段。具体来说，红、蓝、灰三类点的得分依次为50、40和25，得分越高，搜索范围越大。例如得分为50的红点将拥有最广的搜索范围，而得分为25的灰点仅保留有限范围内的基因对。对于重复基因数量超过设定参数“muplite+4”的基因，仅保留灰点类型的同源基因对。这种方式通过缩小两端灰点的搜索范围，降低了共线性区段边缘识别的错误率，同时提升了区段长度与保留的基因对数量。

此外，由于红点具有最高得分，共线性区段更倾向于优先保留红点，以增强其稳定性和准确性。例如，在某一共线性区段（图3B）中，有两个同源点分别被标记为A和B。如果未对这些同源基因对进行排序与打分，则动态规划算法将赋予它们相同的得分，从而无法区分其重要性。

图3. WGDI共线性检测算法改进流程图

(A) WGDI根据基因同源性将同源基因对划分为红色、蓝色和灰色三类点，并赋予不同分数。不同颜色的点对应不同的搜索范围，这种设置不仅降低了共线性区段的错误率，还可延长其长度。

(B) 点的不同得分也有助于增强共线性区段的稳定性。相较之下，若未对同源基因进行排序，则无法有效识别更高同源性（如红点）的基因对。我们使用葡萄（Vitis vinifera）、红豆杉叶树（Cercidiphyllum japonicum）、四合木（Tetracentron sinense）和黑胡椒（Piper nigrum）的基因组，对WGDI与其他主流软件进行了共线性检测性能的比较（详见补充表1–4及补充图1–4），结果表明WGDI在多个系统中均表现出良好的效果。

WGDI的实际应用示例

多倍化推断分析

为展示WGDI在多倍体推断中的应用过程，以黄瓜（Cucumis sativus）这一已知经历多次多倍化事件的植物为例。已有研究推断其基因组经历过两轮多倍化：一次为被子植物核心类群共有的三倍体化事件（WGT，或称γ事件），另一次为较近时期的全基因组重复（WGD）（Huang 等, 2009；Wang 等, 2018）。作为参考，我们选用仅经历过γ事件的葡萄（V. vinifera）基因组（Jaillon 等, 2007）。

多倍化分析分三步进行：首先，算法基于共线性（同源性点图）寻找WGD的证据。使用“-d”参数，WGDI可快速绘制V. vinifera与C. sativus之间的同源区段点图（图4A），以及C. sativus与V. vinifera之间的点图（图4B）。纵向共线性深度为3，与所有核心双子叶植物经历γ事件的推断一致；横向共线性深度可能为2，主要由于红色点未集中在一个共线性区段上。在主要由红点组成的区段中，纵向共线性深度为2（图4B）。结合V. vinifera基因组三组同源染色体的结构，这一结果提示最大共线性深度可能为3×2=6；在红点主导的区段中，其横向共线性深度为1，对应最大深度为3×1=3。综合已有的多倍体事件推断和共线性深度信息，可以构建一幅系统进化树（图4F）。由此可见，WGDI生成的同源点图可适应大多数关于WGD事件的推断模型。

图 4. 以黄瓜（*Cucumis sativus*）和葡萄（*Vitis vinifera*）为例的多倍体推断

(A) 所选葡萄与黄瓜染色体之间同源关系的点阵图。葡萄的6、8和13号染色体是由核心真双子叶植物全基因组三倍化产生的同源三联体。 (B) 所选黄瓜与葡萄染色体之间的同源关系点阵图。图中用矩形标出了外旁系区域或次级匹配区域。 (C) Ks 点阵图，其中基于 Ks 值对共线性区块进行识别并着色。 (D) Ks 分布图。 (E) 两个物种的基因系统发育树。 (F) 使用 ASTRAL-III 构建的比对树推断系统发育关系。

第二步使用 Ks 分布来验证全基因组加倍（WGD）的发生及其时间。使用 “-bk” 程序，可以直观地可视化共线性基因对的 Ks 值（图 4C）。同一共线区块中的基因对 Ks 值波动较小，可以使用其中位数代表该区块的 Ks 分布。不同区块的 Ks 值差异很大，尤其是在区块来源于不同多倍化事件的情况下。通过结合参数和 Ks 分布，可以轻松区分这些区块，并使用 “-pf” 程序输出拟合函数及其最优拟合。目前，许多研究者仍使用高斯混合模型或类似方法拟合多个多倍化事件。但由于高斯混合模型容易过拟合，得到的 Ks 峰可能波动大、不准确（Zwaenepoel 和 Van de Peer，2019）。可使用 “-kf” 程序显示单一或多个物种间的 Ks 分布。可以看出，葡萄与黄瓜共享的三倍化事件的 Ks 峰差异很大，甚至葡萄和黄瓜的分化事件的 Ks 峰比黄瓜最近一次 WGD 的 Ks 峰还要小（图 4D）。由于物种的进化速率差异较大，即使是同一次 WGD，其 Ks 峰也可能有很大不同。因此，必要时需对 Ks 峰进行校正，然后推断多倍化时间（Wang 等，2017，2018；Yang 等，2020）。与基于聚类得到的旁系基因对（如 OrthoMCL 使用的方法）相比，WGDI 推断的 Ks 分布可大大减少串联重复或其他非共线性旁系基因带来的影响。

最后，使用基于基因树的方法验证多倍化推断。在本研究中，使用 “-a” 和 “-at” 程序，获得了葡萄和黄瓜的同源基因列表，并通过 ASTRAL-III v5.7.7 构建的 1138 个基因树推断其系统发育关系（Zhang 等，2018）（图 4E）。其中有 92 个基因树至少包含三个相同的黄瓜基因，占所有基因树的 8.08%。在一些缺失多个同源基因的基因树中，其结构仍支持黄瓜经历了一次较新的 WGD 的假设。总之，WGDI 将三种主要的 WGD 检测方法结合在一起，能够相互验证，帮助研究人员准确、高效地推断多倍化事件。

WGDI 在多层次基因组同源推理中的应用

花生（Arachis hypogaea）是一种异源多倍体，已被证明来源于两个祖先物种——Arachis duranensis 和 Arachis ipaensis 的杂交（Bertioli 等，2016, 2019；Zhuang 等，2019）。在此，我们以花生为例，说明如何通过以下步骤在异源多倍体中推断基因组同源关系：

第一步，使用同源点阵图和 Ks 点阵图对基因组同源性进行分层推理。通过 “-d” 和 “-bk” 程序输出结果可以看出，花生染色体1至10来自 A. duranensis，染色体11至20来自 A. ipaensis。然而，染色体3和13之间显然发生了易位（图 5A）。通过评估不同多倍化事件保留的共线区块的 Ks 值、区块标识等差异，可以使用 “-a” 程序轻松获得三种基因组间的同源基因列表（图 5B）。

第二步，使用比对树进行进一步的分层推理。通过 “-at” 程序，使用来自经历了染色体易位的花生3号染色体、A. duranensis 和 A. ipaensis 染色体的同源基因列表构建了2376棵基因树，并以滑动窗口形式显示所有可能的树结构得分（图 5C）。其中1597棵支持花生起源于 A. duranensis，624棵支持起源于 A. ipaensis，与所推断的染色体易位一致。

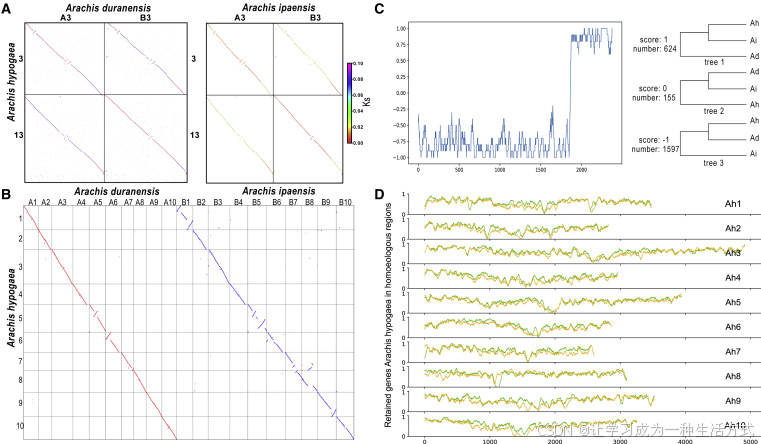
图5. 以落花生（*Arachis hypogaea*）为例进行基因组同源性的分层推断

(A) 同源性点图和Ks值点图，比较选定的落花生（A. hypogaea）、杜兰花生（A. duranensis）和伊帕花生（A. ipaensis）的染色体。图中展示了落花生的染色体3和13，它们是由共有的双子叶植物六倍化事件产生的同源三联体，其匹配的染色体为杜兰花生的染色体3和伊帕花生的染色体4。

(B) 以杜兰花生为参考基因组，对落花生进行的比对结果。

(D) 滑动窗口中落花生同源区域1（橙色）和同源区域组2（绿色）的基因保留率。

最后，通过“–r”和“–p”程序，分别展示了该异源四倍体中的基因保留情况和亚基因组分化情况。在异源四倍体落花生中，来自杜兰花生亚基因组的基因保留数量多于来自伊帕花生亚基因组的（见图5D）。此外，两套亚基因组或祖先二倍体基因组之间的分化（P指数）估计为0.86，说明它们存在显著差异，符合典型异源四倍体的特征。因此，WGDI使用多种方法，基于基因组同源性进行异源多倍化的分层推断，并生成由基因共线性支持的、与异源多倍体物种形成相关的同源基因的分层列表。

WGDI用于追踪祖先染色体核型的应用

葡萄（Vitis vinifera）的染色体核型广泛用作核心双子叶植物核型分析的参考。此前的核型分析表明，葡萄的祖先染色体发生过两次融合和四次断裂（Murat等，2015）。根据核型变化，有人推测耧斗菜（Aquilegia coerulea，毛茛科）是所有核心双子叶植物的亲本祖先之一，可能是一个古老的异源六倍体（Akoz和Nordborg，2019）。然而，我们使用“–km”程序，基于祖先双子叶植物核型（AEK）获得了葡萄和耧斗菜的核型。与之前的核型结果相比，我们在之前的空白区域恢复出了明显的共线性区块（见图6A）。例如，耧斗菜染色体2和染色体3的末端以及染色体5的起始部分对应于葡萄染色体4的中间区域（图6A），该区域是未注释区域（空白区域，参见Akoz和Nordborg，2020年的图6）。如果核型演化基于这些结果，可能会造成误导。

图6. 葡萄（*Vitis vinifera*）染色体4、7和14与耧斗菜（*Aquilegia coerulea*）染色体3和5的核型演化

(A) 选定的耧斗菜和葡萄染色体之间的同源性点图。图中七种不同颜色代表七条祖先单倍体染色体。

(B) 耧斗菜染色体3和5的构建过程。

染色体数目减少与B染色体模型（Wang等，2015；Wang和Wang，2020）为理解真核生物染色体数目及其重排的演化提供了新方法。通过该模型，发现葡萄的祖先核型比以前推测的更加复杂但也更清晰。例如，粉红色和草绿色染色体在靠近各自一端的地方发生了交叉，形成了两个新染色体（图6C）。两段较长的片段融合成葡萄染色体14，之后在该染色体内部发生了倒位。两段较短的片段并未消失，而是与其他染色体融合，最终形成葡萄染色体4。粉红色和绿色染色体也发生了类似的融合，最终形成了现在的染色体7和4。

然而，耧斗菜的核型与葡萄完全不同。绿色染色体插入粉红色染色体，草绿色染色体与蓝色染色体发生交叉，随后分别演化为现在的染色体5和3（图6B）。因此，耧斗菜和葡萄的核型（参见Akoz和Nordborg，2020）并不能作为支持“耧斗菜基因组揭示核心双子叶植物杂交起源”的证据。与之前的研究结果相比，WGDI揭示的新结论可能更准确地反映了祖先染色体重排的动态过程。

讨论

基因共线性的分析可为多倍化研究提供有力的见解，多倍化在许多物种和系统的形成与演化中发挥了重要作用。WGDI尤其适用于识别频繁发生的多倍化事件，尤其是在高质量的染色体级别基因组基础上。该工具提供的分层推断和与WGD事件相关的基因共线性推断，有助于厘清因重复多倍化而复杂化的植物系统发育关系和核型演化。

WGDI在共线性检测方面的表现（见补充表1–4和补充图1–4）与以往工具（Wang等，2006, 2012；Tang等，2017）相当。

此外，WGDI在重建现存物种的祖先染色体核型方面也非常有效和实用。WGD会导致快速的基因组重组和结构变异，从而在新物种中产生新的染色体核型。理解这种核型演化对于评估某些系统位置尚存争议的谱系以及推测灭绝物种的基因组结构具有重要意义（Akoz和Nordborg，2020）。然而，分裂与融合模型（Salse等，2008；Murat等，2010）无法解释祖先基因组的染色体是如何演化为现今核型的（Wang等，2015）。例如，被推测为所有被子植物、单子叶植物和核心双子叶植物祖先核型（Murat等，2017）中，存在大量未注释（空白）区域。在核型演化过程中，共线性或共线性断裂是推断祖先核型的重要特征。相比简单的分裂–融合假说，植物与动物都需要更详细的染色体演化图谱（Akoz和Nordborg，2020）。WGDI能够提取更完整的共线性区块，有助于从祖先染色体中重建详细的核型演化过程。

WGDI采用了基于动态规划的共线性提取算法，并集成了多种用于可视化和分析的计算程序。对分层和事件相关共线性的推断，有助于厘清被反复多倍化干扰的真实系统发育关系。WGDI可通过GitHub（GitHub - SunPengChuan/wgdi: WGDI: A user-friendly toolkit for evolutionary analyses of whole-genome duplications and ancestral karyotypes）免费获取，并支持conda环境和bioconda平台（Grüning等，2018），实现兼容、易于安装和升级的工具使用体验。