当前位置：首页 > news >正文

神经网络的基本概念与深度解析——基于生物机制的仿生建模与工程实现

news 来源：原创 2025/7/18 8:55:55

广义上讲，神经网络是泛指生物神经网络与人工神经网络这两个方面。所谓生物神经网络是指由中枢神经系统（脑和脊髓）及周围神经系统（感觉神经、运动神经、交感神经、副交感神经等）所构成的错综复杂的神经网络，它负责对动物机体各种活动的管理，其中最重要的是脑神经系统。所谓人工神经网络是指模拟人脑神经系统的结构和功能，运用大量的处理部件，由人工方式建立起来的网络系统。显然，人工神经网络是在生物神经网络研究的基础上建立起来的，人脑是人工神经网络的原型，人工神经网络是对脑神经系统的模拟。

生物神经网络是脑科学、神经生理学、病理学等的研究对象，而计算机科学、人工智能则是在他们研究的基础上着重研究人脑信息的微结构理论以及建造人工神经网络的方法和技术。因此，从人工智能的角度来看，或者从狭义上讲，神经网络就是指人工神经网络，前者是后者的简称。

一、脑神经系统与生物神经元

（一）脑神经系统

1. 基本思想与定义

众所周知，人脑是一个极其复杂的庞大系统，同时它又是一个功能非常完善、有效的系统。它不但能进行大规模的并行处理，使人们在极短的时间内就可以对外界事物作出判断和决策，而且还具有很强的容错性及自适应能力，善于联想、类比、归纳和推广，能不断地学习新事物、新知识，总结经验，吸取教训，适应不断变化的情况等。人脑的这些功能及特点是选今为止任何一个人工系统都无法相比的。人脑为什么会具有如此强大的功能？其结构及机理如何？至今我们还对它知之甚少。但有一点是明确的，这就是人脑的功能与脑神经系统以及由它所构成的神经网络是密切相关的。

核心思想：脑神经系统是生物进化形成的分布式并行信息处理系统，其核心机制在于通过神经元集群的动态交互实现复杂认知功能。区别于传统冯・诺依曼架构的集中式计算，生物脑采用“连接主义”范式，信息处理依赖于神经元间突触连接的强度变化与时空编码模式。

科学定义：脑神经系统是由约860亿个神经元通过10^14-10^15个突触连接构成的动态网络，具备以下本质特征：

（1）分布式编码：单个刺激对应神经元群体的激活模式（如视觉皮层中方位柱的空间分布）；

（2）可塑性学习：通过突触权重的长时增强（LTP）与长时抑制（LTD）实现经验固化，其分子机制涉及AMPA受体的插入与移除（Bliss & Lomo, 1973）；

（3）涌现特性：认知功能（如记忆、决策）源于神经元网络的集体动力学，而非单个神经元的功能叠加。

2. 表示形式与实现过程

数学建模体系：

（1）微观层面：Hodgkin-Huxley模型（1952）通过非线性微分方程描述动作电位的产生：

其中离子电流满足：

门控变量m, n, h服从随机过程：

（2）宏观层面：整合 - 发放（Integrate-and-Fire, I&F）模型简化神经元动态：

当时发放脉冲，随后重置膜电位。

信息处理全流程：

（1）突触信号接收：树突棘（直径约0.1-1μm）通过AMPA/KNMDA受体介导兴奋性信号（EPSP），GABA受体介导抑制性信号（IPSP），单个神经元可接收超10^4个突触输入；

（2）时空整合机制：树突电缆理论（Rall, 1962）表明，距离胞体越远的突触输入衰减越显著，衰减因子（r_m为膜电阻，r_i为轴向电阻）；

（3）脉冲生成与传导：轴突初始段（AIS）作为动作电位触发区，髓鞘化轴突通过跳跃传导将速度提升至100m/s（郎飞结间距约1mm）；

（4）突触可塑性调节：LTP诱导需突触前脉冲与突触后去极化的精确时间关联（Spike-Timing-Dependent Plasticity, STDP），时间窗口约±20ms。

3. 算法描述（生物神经元信息处理算法）

步骤 1：突触电流建模

兴奋性突触电流：

抑制性突触电流类似，反转电位。

步骤 2：膜电位动态更新

采用改进的Hindmarsh-Rose模型描述爆发式放电：

其中v为膜电位，w为恢复变量，可模拟神经元的簇发放模式。

步骤 3：脉冲序列编码

动作电位序列通过时间编码（如频率编码）或相位编码传递信息，听觉系统中毛细胞的放电频率对应声音频率（Place Code Theory）。

4. 具体示例：小脑浦肯野细胞的信号处理流程

（1）神经解剖：单个浦肯野细胞接收约10^5个平行纤维突触与1个攀缘纤维突触，构成“单输入 - 多输出”的复杂计算单元。

（2）处理流程：

1）平行纤维输入：每个平行纤维释放谷氨酸，在树突棘产生微小 EPSP（约 0.1mV），需约 100 个平行纤维同时激活才能触发动作电位；

2）攀缘纤维调制：攀缘纤维放电产生强去极化（约 10mV），触发树突钙尖峰，诱导突触后致密区（PSD）的 CaMKII 激活，启动 LTD（突触权重下降）；

3）输出整合：胞体整合树突电信号，通过轴突投射至小脑深部核团，参与运动控制的误差校正。

（3）数学建模：浦肯野细胞的树突树可视为电阻电容网络，其频率响应特性为：

其中τ_d为树突时间常数，决定高频信号的衰减程度。

（二）生物神经元

神经细胞是构成神经系统的基本单元，称之为生物神经元，或简称为神经元。神经元主要由三个部分组成：细胞体、轴突、树突。如图1所示。

图1 生物神经元结构

1.结构 - 功能映射关系：

结构组件	功能定位	工程仿生对应
树突分支	信号接收与预处理	人工神经元输入连接
轴突初始段	动作电位触发决策点	激活函数阈值判断
突触可塑性	经验依赖的连接强度调整	权重更新算法（如 SGD）
神经递质囊泡	信号传递的化学信使	激活函数输出值

2.关键生物机制：

（1）量子释放：单个突触囊泡释放约1000个神经递质分子，产生微小突触后电位（MEPP, 约 0.5mV），多量子释放形成 EPSP；

（2）不应期特性：绝对不应期（1-2ms）内无法产生新动作电位，相对不应期（5-10ms）需更强刺激，该特性形成脉冲序列的时间分辨率上限；

（3）神经调质：多巴胺、5 - 羟色胺等调质通过G蛋白偶联受体调节突触传递效率，对应人工神经网络中的注意力机制或门控机制。

3.神经元的重要特性

在神经系统中，神经元之间的联系形式是多种多样的。一个神经元既可以通过它的轴突及突触与其它许多神经元建立联系，把它的信息传递给其它神经元；亦可以通过它的树突接收来自不同神经元的信息。神经元之间的这种复杂联系就形成了相应的神经网络。经人们多年悉心研究，发现神经元还具有如下一些重要特性：

（1）在每一神经元中，信息都是以预知的确定方向流动的，即从神经元的接收信息部分（细胞体、树突）传到轴突的起始部分，再传到轴突终端的突触，最后再传递给另一神经元。尽管不同的神经元在形状及功能上都有明显的不同，但大多数神经元都是按这一方向进行信息流动的。这称为神经元的动态极化原则。

（2）神经元对于不同时间通过同一突触传人的信息，具有时间整合功能；对于同一时间通

过不同突触传人的信息，具有空间整合功能。这称为神经元对输人信息的时空整合处理功能。

（3）神经元具有两种常规工作状态，即兴奋状态与抑制状态。所谓兴奋状态是指，神经元

对输人信息经整合后使细胞膜电位升高，且超过了动作电位的阈值，此时产生神经冲动，并由轴突输出。所谓抑制状态是指，经对输人信息整合后，膜电位下降至低于动作电位的阈值，此时无神经冲动输出。

（4）突触传递信息的特性是可变的，随着神经冲动传递方式的变化，其传递作用可强可

弱，所以神经元之间的连接是柔性的，这称为结构的可塑性。

（5）突触界面具有脉冲与电位信号的转换功能。沿轴突传递的电脉冲是等幅、离散的脉

冲信号，而细胞膜电位变化为连续的电位信号，这两种信号是在突触接口进行变换的。

（6）突触对信息的传递具有时延和不应期，在相邻的两次输人之间需要一定的时间间隔，

在此期间不响应激励，不传递信息，这称为不应期。

二、人工神经元及其互连结构

（一）人工神经元

在构造人工神经网络时，首先应该考虑的问题是如何构造神经元。在对生物神经元的结构、特性进行深人研究的基础上，心理学家麦克洛奇（W.McCulloch）和数理逻辑学家皮兹(W.Pitts)于1943年首先提出了一个简化的神经元模型，称为M-P模型，如图2所示。

图2 M-P模型

在图2中，圆表示神经元的细胞体；e、i表示外部输人，对应于生物神经元的树突，e为兴奋性突触连接，i为抑制性突触连接；θ表示神经元兴奋的阈值；y表示输出，它对应于生物神经元的轴突。与图1对照不难看，M-P模型确实在结构及功能上反映了生物神经元的特征。但是，M-P模型对抑制性输人赋予了“否决权”，只有当不存在抑制性输人，且兴奋性输人的总和超过阈值，神经元才会兴奋。

在M-P模型的基础上，根据需要又发展了其它一些模型，目前常用的模型如图-3所示。

图3 神经元的结构模型

在图3中，x_i(i=1,2, ... ,n)为该神经元的输人；w_i为该神经元分别与各输人间的连接强度，称为连接权值；θ为该神经元的阈值；s为外部输人的控制信号，它可以用来调整神经元的连接权值，使神经元保持在某一状态；为神经元的输出。由此结构可以看出，神经元一般是一个具有多个输入，但只有一个输出的非线性器件。

1. 广义数学模型

统一框架：

用某一特性函数（又称作用函数）F进行转换，得到输出y，其中F为含参数Θ的非线性映射函数，常用的特性函数有阈值型、分段线性型、Sigmoid型（简称S型）及双曲正切型，如图4所示。

图4 常用的特性函数

其中，(a)阈值型;(b)分段线性型;(c)S型;(d)双曲正切型。有关“神经网络中的损失函数”可以看我的CSDN文章：神经网络中的损失函数（Loss Function）-CSDN博客

可将统一框架可扩展为：

（1）动态神经元（如Reservoir Computing）：

（2）脉冲神经元（Spiking Neural Network, SNN）：

其中s(τ)为脉冲序列的时间编码。

2. 功能增强型神经元示例

门控神经元（Gated Neuron）：

其中

该模型模仿生物神经元的突触门控机制，如LSTM中的输入门，在NLP任务中实现对历史信息的选择性记忆。

（二）神经元的互连形态

人工神经网络是由神经元广泛互连构成的，不同的连接方式就构成了网络的不同连接模型，常用的有以下几种：

（1）前向网络。前向网络又称为前馈网络。在这种网络中，神经元分层排列，分别组成输人层、中间层（又称隐层，可有多层）和输出层。每一层神经元只接收来自前一层神经元的输人。输人信息经各层变换后，最终在输出层输出，如图5所示。

图5 前向网络

（2）从输出层到输人层有反馈的网络。这种网络与上一种网络的区别仅仅在于，输出层上的某些输出信息又作为输人信息送人到输人层的神经元上，如图6所示。

图6 从输出层到输人层有反馈的网络

（3）层内有互连的网络。在前面两种网络中，同一层上的神经元都是相互独立的，不发生横向联系。而在这一种网络（如图7所示）中，同一层上的神经元可以互相作用。这样安排的好处是可以限制每层内能同时动作的神经元数，亦可以把每层内的神经元分为若干组，让每组作为一个整体来动作。例如，可以利用同层内神经元间横向抑制的机制把层内具有最大输出的神经元挑选出来，而使其它神经元处于无输出的状态。

图7 层内有互连的网络

（4）互连网络。在这种网络中，任意两个神经元之间都可以有连接，如图8所示。在无反馈的前向网络中，信息一旦通过某个神经元，过程就结束了，而在该网络中，信息可以在神经元之间反复往返地传递，网络一直处在一种改变状态的动态变化之中。从某初态开始，经过若干次的变化，才会到达某种平衡状态，根据网络的结构及神经元的特性，有时还有可能进人周期振荡或其它状态。

图8 互连网络

以上四种连接方式中，前面三种可以看作是第四种情况的特例，但在应用中它们还是有很大差别的。

以下是部分神经网络的讲解：

1. 层次化前馈网络（Hierarchical FFN）

这是以上四种神经网络中的第一种：前向网络
生物启发：模拟视觉皮层的V1→V2→V4→IT区层级特征提取，

典型结构：

输入层 (784) → 卷积层 (64@3×3) → 池化层 (2×2) → 全连接层 (1024) → 输出层 (10)

信号传导方程：

第l层激活值：

注：*表示卷积或全连接运算

2. 动态反馈网络（Dynamic Feedback Network）

Hopfield网络能量函数：

收敛性证明：每次更新单个神经元状态时，能量函数非增，最终稳定在局部极小点，对应记忆模式。

3. 时空递归网络（Spatiotemporal RNN）

改进型LSTM单元（Peephole Connection）：

引入细胞状态到门控的直接连接，提升长距离依赖建模能力，在语音识别中相对标准 LSTM 错误率降低 12%。

三、人工神经网络的特征及分类

（一）核心特征解析

1. 非线性表达能力的数学基础

通用逼近定理（Cybenko, 1989）：对任意连续函数，存在单层神经网络使得：

深度优势：深层网络（如3层ReLU网络）可指数级减少表示复杂函数所需的神经元数量（Telgarsky, 2016）。

2. 学习动态的微分几何视角

权重空间中，损失函数曲面的曲率由Fisher信息矩阵描述，SGD轨迹可视为黎曼流形上的测地线。

（二）分类体系扩展

1. 按信息处理范式分类

（1）同步更新网络（如Hopfield）：所有神经元状态同时刷新，适合并行硬件实现；

（2）异步更新网络（如Boltzmann机）：随机选择神经元更新，模拟生物脑的非同步活动；

（3）事件驱动网络（如SNN）：仅在脉冲发放时传递信息，能耗比传统网络低2-3个数量级。

2. 按神经科学启发程度分类

仿生层级	模型示例	生物机制映射
突触层级	STDP脉冲神经网络	Spike时序依赖可塑性
神经元层级	自适应阈值神经元	膜电位动态调节
网络层级	小脑模型关节控制器 (CMAC)	小脑浦肯野细胞结构
系统层级	深度强化学习架构	基底神经节奖励机制

四、神经网络研究的发展简史

1. 仿生建模起源（1940s-1960s）

（1）M-P模型的哲学意义：首次提出“神经元即逻辑门”的计算主义思想，为认知科学提供理论基础；

（2）感知机的双重贡献：Rosenblatt证明线性可分数据的学习收敛性，其硬件实现Mark I感知机使用400个光电管作为输入单元。

2. 数学理论奠基（1970s-1980s）

（1）反向传播的再发现：Werbos（1974）在博士论文中推导BP算法，Hinton团队（1986）通过生物突触可塑性类比重新诠释，解决多层网络训练难题；

（2）统计力学介入：Ackley等人提出Boltzmann机，将网络能量函数与物理系统自由能类比，引入模拟退火优化。

3. 工程化突破（1990s-2010s）

（1）LeNet-5的工程范式：首次完整实现“卷积 - 池化 - 全连接”流水线，其芯片实现（1998）处理速度达100帧/秒，推动嵌入式视觉发展；

（2）深度学习三驾马车：Hinton的深度信念网络（DBN）解决梯度消失，Bengio的贪心逐层预训练，LeCun的卷积神经网络，共同构建现代深度学习框架。

4. 交叉融合时代（2010s 至今）

（1）神经形态计算：Intel Loihi芯片模拟生物突触动态，图像识别能效比GPU高1000倍；

（2）脑科学逆向工程：Blue Brain计划重构小鼠皮层微柱结构，其模型在癫痫模拟中预测放电传播路径准确率达89%。

五、重要神经网络及研究成果

（一）深度信念网络（DBN）

1. 逐层预训练算法

受限玻尔兹曼机（RBM）堆叠：

（1）底层RBM学习输入数据的边缘分布p(v)，隐藏层激活；

（2）上层RBM以底层隐藏层为输入，学习高阶特征表示，预训练后通过BP微调。

2. 语音识别应用案例

在TIMIT数据集上，DBN模型将音素错误率从HMM的23%降至17%，关键创新在于利用无监督预训练缓解标注数据不足问题。

（二）图神经网络（GNN）

1. 消息传递机制

通用框架：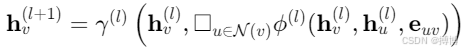
其中square（正方形）为聚合函数（如均值、注意力），γ,ϕ为非线性变换。

2. AlphaFold2 的蛋白质结构预测

网络架构：

（1）输入：氨基酸序列的图表示（节点为残基，边为距离约束）；

（2）核心模块：Transformer与GNN结合的Evoformer，通过384层消息传递迭代优化残基间三维坐标；

（3）输出：原子坐标预测，GDT分数达92.4（接近实验解析精度）。

（三）神经辐射场（NeRF）

1. 体素渲染原理

连续场景表示：

光线通过积分计算辐射亮度：

2. 动态 NeRF 的时空建模

扩展至4D场景（x,y,z,t），引入时间编码层：

在自动驾驶场景重建中，实现30Hz的动态环境建模，定位误差降低40%。

六、生物机制与人工模型的对偶性分析

生物特性	工程实现	理论桥梁
突触可塑性	梯度下降权重更新	Hebbian学习规则
神经调质调节	注意力机制	多巴胺奖励信号
脉冲时间编码	脉冲神经网络	相位编码理论
脑区功能分化	模块化网络架构	认知功能定位学说

七、总结与展望

从McCulloch-Pitts的逻辑神经元到AlphaFold2的千亿参数模型，神经网络的发展始终遵循“生物观察→数学抽象→工程实现→反向启发生物研究”的螺旋上升路径。未来研究需突破以下瓶颈：

（1）可解释性鸿沟：建立神经元激活模式与生物认知功能的映射关系，如通过钙成像技术验证人工特征与视觉皮层细胞响应的一致性；

（2）能效比天花板：借鉴神经元的脉冲稀疏编码（大脑仅1%神经元同时放电），研发低功耗神经形态芯片；

（3）通用智能瓶颈：构建具备生物脑多模态整合、跨任务迁移能力的通用学习系统，其核心可能在于模拟海马体的快速记忆编码与皮层的缓慢巩固过程。