当前位置：首页 > news >正文

Lebesgue测度和积分理论发展概观

news 来源：原创 2025/5/10 17:18:49

1. 发展背景

积分可以从两个角度来理解。首先，积分是微分的逆函数，因此积分是反导数(译注：但积分是独立于微分的，不能微分的函数也可能可积)。然而，这是一个非常抽象的概念。其次，两点之间的积分可以看作是计算至少有一条边不是直的、而是根据某个函数变化的形状面积的方法。虽然计算正方形或三角形的面积很简单，但计算例如“D”形或“B”形的面积在数学上要困难得多。通常，这些问题被认为是在绘制的图形上求曲线下的面积，教科书中通常也是这样描述的。

许多古希腊数学家都关注过这类问题。他们掌握了计算正方形、三角形和其他规则形状面积的方法，但一旦物体出现曲线，计算起来似乎就不可能了。Archimedes(公元前 287-212 年)等思想家考虑了各种方法。其中一种流行的方法是使用上限和下限的概念。如果你选取想要测量的形状，画一个刚好能容纳这个不规则形状的正多边形，那么不规则形状的面积就会有一个下限。然后，再画一个刚好完全包围这个不规则形状的正多边形。这样就给出了该形状的上限，因此实际面积必定位于两个绘制的面积之间。如果一个规则形状不够接近，可以像拼图一样将几个规则形状拼在一起。虽然这种方法可以得到近似值，但在某种意义上，这是一种弄巧成拙的方法，因为你永远无法得到正确答案。

几个世纪后，欧洲数学家如Johannes Kepler(1571-1630)在面积计算中引入了无穷小量。无穷小量被认为是小于任何实际有限但又不完全为零的量。虽然这个想法有点奇怪，但它的影响很大。第一本关于积分方法的教科书由 Bonaventura Cavalieri(1598-1647)于 1635 年出版，但其形式今天已无法辨认。不同的思想家对积分法进行了进一步的修改，每个人都使用自己独特的方法来近似曲线下的面积。许多方法对一种曲线很有效，但对其他曲线则效果不佳。当 Isaac Newton(1643-1727)和Gottfried von Leibniz (1646-1716)分别研究微积分并开发出一种更通用的求曲线下面积的方法时，现代积分形式开始成形。关于谁最先发现这个想法，随后发生了一场激烈的争论。Newton在短期内获胜；他匿名撰写的攻击Leibniz的文章数不胜数，充满侮辱和恶毒。然而，从长远来看，Leibniz更简洁的风格和符号对数学的影响更大。

Augustin Cauchy(1789-1857)和Karl Weierstrass(1815-1897)等数学家进一步完善了积分。无穷小量的概念被极限的概念所取代，从某种意义上说，这又回到了Archimedes的思想。Cauchy赋予了初等微积分至今仍沿用的形式。许多现代积分概念都源于他提出的积分是和的极限而非简单的反导数的概念。

十九世纪中叶，Bernhard Riemann(1826-1866)对积分进行了更精确的定义，扩展了该方法适用的函数。在接下来的几十年里，他的工作又被许多理论家修改，使其应用范围更加广泛。

然而，到了十九世纪末，Riemann积分的许多例外变得显而易见。在积分学以及许多其他数学领域，年轻的数学家们热衷于寻找违反规则的案例，这些案例被称为“病态案例”。对于Riemann积分来说，这些案例通常是具有许多不连续点的函数，也就是说，曲线并非平滑流畅，而是存在间隙或极端瞬时变化的点。另一个问题是，积分与微分之间的反比关系似乎不成立的情况很多。由于积分的一种处理方式是将其视为微分的对立面，因此发现这种关系不成立的情况表明整个领域都出了问题。许多资深数学家担心他们周围的数学正在崩溃，因为这门学科的整个基础似乎都受到了攻击。一些批评家呼吁彻底放弃积分。

2. Lebesgue测度和积分理论的发展

在19 世纪，德国数学家Karl Weierstrass 为新兴的分析学科奠定了严谨的基础。然而，现代分析与Weierstrass时代的分析在许多方面有所不同，最明显的是抽象程度。当今的分析设置于各种一般情境中，其中实线和复平面(将在复分析部分解释)仅仅是两个相当简单的例子。

Henri Lebesgue出人意料地成为积分学的救星。他的大学生涯虽然表现良好，但并不出众。在法国巴黎高等师范学院完成学业后，他在图书馆工作了两年，在此期间，他阅读了另一位应届毕业生René Baire(1874-1932)的论文。Baire于1899年撰写的博士论文涉及不连续函数的研究，而这类病态函数正是无法用 Riemann积分法解决的。Baire的健康状况不佳限制了其进一步的研究，但Lebesgue看到了这些思想的潜力。

Lebesgue也受到了其他一些数学家的影响。Camille Jordan(1838-1922)运用测度的概念扩展了Riemann积分。Emile Borel(1871-1956) 彻底修改了集合中测度和可测性的概念。测度的数学概念难以用文字解释，因为它在数学上非常复杂。它是我们熟悉的长度、面积、体积测量概念的扩展，推广到更广泛的集合体系，因此处理的是抽象空间。

Borel在其著作中运用了集合论领域的激进新思想，特别是Georg Cantor(1845-1918)颇具争议的著作。Cantor的集合论遭到一些数学家的强烈反对，因为它处理无穷大的方式与一些哲学和宗教教义相矛盾。数学家以及更广泛的知识界长期以来一直对无穷大的概念感到不安，而Cantor关于某些无穷量比其他无穷量更大的论证，对一些人来说似乎有些过头了。

Lebesgue将所有这些不同的元素结合在一起，彻底改变了积分学。1901年，他提出了测度论(theory of measure)。这扩展了Jordan和Borel的思想，并极大地增强了这一概念的普遍性。他提出的定义至今仍被称为Lebesgue测度。然而，更重要的是，它也对积分学产生了影响。下面将介绍Lebesgue的贡献，他的贡献使得被称为测度论的分析分支成为可能。

在Lebesgue的时代，数学家们已经注意到 Riemann 定义积分的方式存在诸多缺陷。(Riemann积分在“积分”一节中有解释。) 许多具有合理性质的函数最终被证明不具有Riemann意义上的积分。此外，某些求极限方法，当应用于函数序列而非数字序列时，在积分方面会表现出非常奇怪的行为。一些数学家尝试开发更好的积分定义方法，其中最好的是Lebesgue的方法。

例如，考虑这样一个函数 f ：当 x 是比率数(rational)时, f (x) = 0 , 当 x 是非比率数(irrational)时, f (x) = 1 。则对于

$\displaystyle \int_{0}^{1}f(x)dx$ ,

什么值才是有意义的？根据Riemann的定义，该函数不具有良定义的积分(即定义明确的积分)。原因是，在任何区间内，它的值都为0和1，因此它在这两个值之间剧烈波动。遗憾的是，对于这个例子来说，Riemann积分基于这样的假设：在足够小的区间内，函数值的变化幅度非常小。

然而，在某种意义上，比率数在实数中所占的比例非常小。事实上，“几乎所有”实数都是非比率数。具体来说，所有比率数的集合可以被一组区间包围，这些区间的总长度可以任意小(译注：任意小的区间内都有无数比率数)。因此，在良定的意义上，比率数集的“长度”为零。有充分的理由说明，长度为零的集合上的值不应该影响函数的积分——基于该集合的“矩形”在任何合理的解释中都应该具有零面积。即便如此，如果函数 f 的定义被改变，使其在比率数上取值为 1 而不是 0，它的积分也不应该改变。然而，得到的函数 g 现在对所有 x 都采用 g(x) = 1 的形式，并且该函数确实具有Riemann积分。事实上，

$\displaystyle \int_{a}^{b}f(x)dx=b-a$ 。

Lebesgue推断，同样的结果也应该适用于 f ——但他知道，如果积分按照Riemann的方式定义，则不会如此。

Riemann方法对 f 不起作用的原因是， f 的值在任意小的区间内剧烈波动。Riemann的方法依赖于通过在垂直方向上将图切分成非常薄的片来近似图下的面积，如图所示。他的方法的问题在于垂直方向：垂直切片允许切片内函数值发生剧烈变化。因此，Lebesgue改为水平切图(见图)。这种切片内的变化不超过切片的厚度，并且可以使其非常小。然而，为了保持较小的变化，需要付出的代价是，f (x) 位于给定水平切片中的 x 集可能非常复杂。例如，对于之前定义的函数 f，每当 x 为比率数时，f (x) 位于 0 附近的薄片中；每当 x 为非比数时，f (x) 位于 1 附近的薄片中。

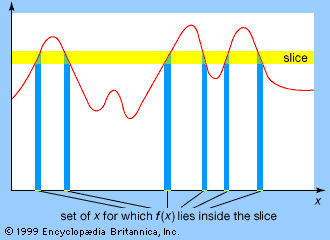
------------------------------Lebesgue积分。请注意，要求和的面积(或切片)是水平的，而不是垂直的。其中一个黄色切片表示位于蓝色条形底部的(不相交)集合，该集合对应于该切片的取值范围。----------------------------------------

然而，这样的集合是否复杂并不重要：它只要具有明确定义的广义长度就足够了。那么，f 图像中对应于给定水平切片的部分将具有明确定义的近似面积，该面积通过将确定切片的函数值乘以其函数值位于该切片内的 x 集的“长度”来求得。因此，Lebesgue面临的核心问题根本不是积分本身；而是将长度的概念推广到足够复杂的集合。Lebesgue做到了。基本上，他的方法是将集合封闭在区间的集合中。由于集合的广义长度肯定小于区间的总长度，因此剩下的就是选择使总长度尽可能小的区间。

这种广义的长度概念被称为Lebesgue测度。一旦建立了测度，就可以定义Lebesgue对Riemann积分的广义定义，而且事实证明，它远胜于Riemann积分。测度的概念可以得到相当大的扩展——例如，扩展到高维空间，在那里它可以推广面积和体积等概念——从而产生被称为测度论的分支学科。测度论的一个基本应用是概率论和统计学，这是Kolmogorov在20世纪30年代开创的一项发展。

3. 影响

Arnard Denjoy(1884-1974)扩展了Lebesgue积分的定义(Denjoy 积分)，而Alfred Haar(1885-1933）则做了进一步的研究(Haar积分)。另一位数学家将Lebesgue的思想与他同时代的T. J. Stieltjes(1856-1894)的思想相结合，提出了Lebesgue- Stieltjes积分——这是积分的又一次扩展，允许包含更多函数。Lebesgue及其追随者所做的工作使一些人认为，虽然积分的概念至少与Archimedes一样古老，但积分理论却是20世纪的产物。

Lebesgue的思想复杂而抽象。事实上，他的测度和积分思想通常只在大多数大学的研究生阶段教授。在大多数情况下，Riemann积分仍在使用，全球绝大多数本科微积分课程仍使用Riemann定义来解释积分。大多数初等微积分课程甚至没有深入探讨Riemann的思想，而Cauchy微积分的形式至今仍在教授。然而，尽管Lebesgue的思想可能抽象且难以理解，但积分领域在各个层面的持续成功和数学可行性，很大程度上要归功于他为复兴这门学科所做的努力。

1. 发展背景

2. Lebesgue测度和积分理论的发展

3. 影响

相关文章：