当前位置：首页 > news >正文

【机器学习】朴素贝叶斯

news 来源：原创 2025/5/24 7:17:03

一、朴素贝叶斯的算法原理

1.1 定义

1.2 贝叶斯定理

1.3 条件独立性假设

二、朴素贝叶斯算法的几种常见类型

2.1 高斯朴素贝叶斯 (Gaussian Naive Bayes)

【训练阶段】 - 从数据中学习模型参数

【预测阶段】 - 对新样本 Xnew 进行分类

2. 2 多项式朴素贝叶斯 (Multinomial Naive Bayes)

【训练阶段】 - 学习模型参数

【预测阶段】 - 对新样本 Xnew 进行分类

2.3 伯努利朴素贝叶斯 (Bernoulli Naive Bayes)

【训练阶段】 - 学习模型参数

【预测阶段】 - 对新样本 Xnew 进行分类

三、实例：基于朴素贝叶斯的好瓜预测

任务：对一个给定的西瓜样本进行二分类（好瓜/坏瓜）

1.训练数据

2.测试数据

3.计算步骤

4.代码实现

四、学习总结

一、朴素贝叶斯的算法原理

1.1 定义

朴素贝叶斯是一种基于 贝叶斯定理 的 概率分类算法。它属于 监督学习 算法的一种，也就是说，它需要一个带有标签（即正确答案）的训练数据集来学习。

它的核心思想是：对于一个未知类别的数据样本，计算该样本 属于各个类别的概率，然后选择 概率最大的那个类别 作为它的预测类别。

1.2 贝叶斯定理

贝叶斯定理描述了在已知某些条件下，一个事件发生的概率。

在分类问题中，我们想知道的是：在看到了某个数据样本的特征（X）之后，这个样本属于某个类别（y）的概率是多少？

这个概率被称为 后验概率 (Posterior Probability)，用数学公式表示就是 P(y∣X)。

贝叶斯定理的公式如下：

$P(y|X) = \frac{P(X|y)P(y)}{P(X)}$

其中

P(y∣X): 后验概率 (Posterior Probability)

P(X∣y): 似然性 (Likelihood)

在 假设样本属于类别 y 的前提下，观察到特征数据 X 的概率。

P(y): 先验概率 (Prior Probability)

在 观察到任何特征数据 X 之前，认为样本属于类别 y 的概率。

P(X): 证据 (Evidence)

观察到特征 X 的概率。这是一个归一化因子，确保所有类别的后验概率加起来等于1。在分类任务中，对于所有类别，P(X) 的值都是相同的。因此，在比较不同类别的后验概率 P(y∣X) 时，我们 只需要比较分子 P(X∣y)P(y) 的大小即可，可以忽略分母 P(X)。

所以，我们的目标简化为：计算每个类别 y 的 P(X∣y)P(y) 值，哪个类别的这个值最大，就预测样本属于哪个类别。

1.3 条件独立性假设

计算似然性 P(X∣y) 看似简单，但 X 通常包含多个特征 (x1,x2,...,xn)。

直接计算 P(x1,x2,...,xn∣y) 是非常困难的，因为它需要考虑所有特征之间的复杂联合关系，这需要极大的数据集才能准确估计。

为了简化计算，“朴素”贝叶斯算法引入了一个关键的假设：

给定类别 y 的条件下，所有特征 X=(x1,x2,...,xn) 之间是相互条件独立的

这意味着：

$P(X|y)=P(x_{1},x_{2},...,x_{n}|y)\approx P(x_{1}|y)\times P(x_{2}|y)\times...\times P(x_{n}|y)$

二、朴素贝叶斯算法的几种常见类型

朴素贝叶斯算法的核心思想基于 贝叶斯定理 和 特征条件独立性假设 。

不同的朴素贝叶斯变体主要是因为它们对 特征数据的概率分布 P(xi∣y) 做出了不同的假设。

根据特征数据类型的不同，最常见的朴素贝叶斯分类器有以下三种：

高斯朴素贝叶斯 (Gaussian Naive Bayes)
多项式朴素贝叶斯 (Multinomial Naive Bayes)
伯努利朴素贝叶斯 (Bernoulli Naive Bayes)

2.1 高斯朴素贝叶斯 (Gaussian Naive Bayes)

主要用于处理 连续型特征

【训练阶段】 - 从数据中学习模型参数

1.计算先验概率 P(y)

统计训练数据中每个类别 y出现了多少次。
用每个类别的样本数除以总样本数，得到该类别的先验概率。
公式：

2.按类别分组数据

将训练数据按照类别标签分开，方便后续计算。

3.计算每个类别下每个特征的均值 μy,i 和标准差 σy,i

对每一个类别 y：

对该类别下的每一个连续特征 xi：
- 计算这个特征在 只属于类别 y 的样本 中的 平均值 μy,i
- 计算这个特征在 只属于类别 y 的样本 中的 标准差 σy,i

4.处理零标准差情况

如果在某个类别 y 下，某个特征 xi 的所有值都完全相同，那么计算出的标准差 σy,i 会是 0。这在后续计算高斯概率密度时会导致除零错误。
解决方法： 检查是否有 σy,i=0 的情况。如果存在，将其替换为一个非常小的正数，或者使用更复杂的方差平滑技术。

5.存储模型参数

保存好计算出的所有类别的先验概率 P(y)，以及每个类别下每个特征的均值 μy,i 和（处理过的）标准差 σy,i。

【预测阶段】 - 对新样本 Xnew 进行分类

假设新样本 Xnew 包含特征值 (x1,x2,...,xn)

1.为每个可能的类别 y 计算得分

初始化得分： 通常取先验概率的对数：

累加特征的对数似然： 对于新样本中的 每一个连续特征 xi：

取出训练阶段为类别 y 和特征 i 存储的均值 μy,i 和标准差 σy,i。
使用 高斯概率密度函数 (PDF) 公式 计算该特征值 xi 在类别 y 模型下的概率密度：

将计算得到的 logPDF(xi∣y) 加到对应类别 y 的得分上：

2.比较得分并预测

对所有可能的类别 y 都执行完步骤 1 后，比较它们最终的 Score
得分最高的那个类别，就是高斯朴素贝叶斯对新样本 Xnew 的预测结果。

2. 2 多项式朴素贝叶斯 (Multinomial Naive Bayes)

特征是离散的，通常表示某件事发生的次数或频率

【训练阶段】 - 学习模型参数

1.计算先验概率 P(y)

同高斯朴素贝叶斯

2.按类别分组数据

同高斯朴素贝叶斯

3.统计特征计数 Nyi 和总计数 Ny

确定整个数据集的 特征词汇表（所有出现过的不同特征/单词）。

设词汇表大小（或总特征数）为 k。

对每一个类别 y：

计算 Ny：该类别下 所有样本 中，所有特征 出现的 总次数 之和。
对词汇表中的每一个特征 xi：
- 计算 Nyi：该类别下 所有样本 中，特征 xi 出现的 总次数。

4.选择平滑参数 α

通常使用拉普拉斯平滑，即 α=1

5.存储模型参数

保存先验概率 P(y)，所有类别的总特征数 Ny，每个类别下每个特征的计数 Nyi，以及词汇表大小 k 和平滑参数 α。

【预测阶段】 - 对新样本 Xnew 进行分类

假设新样本 Xnew 由特征计数 (count(x1),count(x2),...,count(xk)) 表示，其中 count(xi) 是特征 i 在 Xnew 中出现的次数。

1.为每个可能的类别 y 计算得分

初始化得分：

累加特征的对数似然： 对于词汇表中的 每一个特征 xi (从 i=1 到 k)：

取出训练阶段为类别 y 存储的 Nyi, Ny
使用 平滑公式计算条件概率 P(xi∣y)：

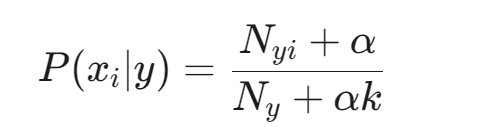
获取该特征 xi 在 新样本 Xnew 中的计数 count(xi)。
将该特征对得分的贡献（其计数值乘以其对数概率）累加到对应类别 y 的得分上：

这里体现了出现次数越多的特征，对总得分的影响越大

2.比较得分并预测

比较所有类别的最终 Score
得分最高的类别即为预测结果。

2.3 伯努利朴素贝叶斯 (Bernoulli Naive Bayes)

特征是二元的（0/1），表示某事物是否存在、发生与否。

【训练阶段】 - 学习模型参数

1.计算先验概率 P(y)

同高斯朴素贝叶斯。

2.按类别分组数据

同高斯朴素贝叶斯。

3.统计特征出现次数 Ny,xi=1 和类别总数 Ny

确定所有可能的二元特征列表

对每一个类别 y：

计算 Ny：属于该类别的 样本总数

对每一个特征 xi:

计算 Ny,xi=1：在类别 y 的样本中，特征 xi 出现过（值为1）的样本数量。

4.选择平滑参数 α

通常 α=1

5.存储模型参数

保存先验概率 P(y)，每个类别下每个特征的出现次数 Ny,xi=1，以及每个类别的总样本数 Ny

【预测阶段】 - 对新样本 Xnew 进行分类

假设新样本 Xnew 由二元特征向量 (x1,x2,...,xk) 表示，其中 xi∈{0,1}。

1.为每个可能的类别 y 计算得分

初始化得分：

累加特征的对数似然： 对于 每一个特征 xi (从 i=1 到 k)：

取出训练阶段为类别 y 存储的 Ny,xi=1 和 Ny

计算特征 i 在类别 y 下出现的概率 P(xi=1∣y):

计算特征 i 在类别 y 下不出现的概率 P(xi=0∣y)

根据新样本 Xnew 中特征 xi 的值，选择对应的概率并累加其对数：

如果 Xnew 中 xi=1（特征出现），则 ${Score}_y = \text{Score}_y + \log P(x_i = 1|y)$
如果 Xnew 中 xi=0（特征未出现），则 ${Score}_y = \text{Score}_y + \log P(x_i = 0|y)$

2.比较得分并预测

比较所有类别的最终 Score
得分最高的类别即为预测结果

三、实例：基于朴素贝叶斯的好瓜预测

目标是根据一系列已知特征，判断一个西瓜是“好瓜”（标记为“是”）还是“坏瓜”（标记为“否”）。

任务：对一个给定的西瓜样本进行二分类（好瓜/坏瓜）

1.训练数据

数据集摘要:

总样本数: 17
好瓜 (是) 数量: 8
坏瓜 (否) 数量: 9

2.测试数据

3.计算步骤

使用拉普拉斯平滑和高斯分布假设，方差使用N作为分母

计算后验概率

比较结果

计算出的 "好瓜=是" 的得分 (0.02177) 远大于 "好瓜=否" 的得分 (0.000036)

结论

根据朴素贝叶斯分类器的计算结果，对于测试样本 "测1"（特征为青绿, 蜷缩, 浊响, 清晰, 凹陷, 硬滑, 密度=0.697, 含糖率=0.460），预测结果为 是 (好瓜)。

4.代码实现

import pandas as pd
import math# 1. 数据准备 
data = {'色泽': ['青绿', '乌黑', '乌黑', '青绿', '浅白', '青绿', '乌黑', '乌黑', '乌黑', '青绿', '浅白', '浅白', '青绿', '浅白', '乌黑', '浅白', '青绿'],'根蒂': ['蜷缩', '蜷缩', '蜷缩', '蜷缩', '蜷缩', '稍蜷', '稍蜷', '稍蜷', '稍蜷', '硬挺', '硬挺', '蜷缩', '稍蜷', '稍蜷', '稍蜷', '蜷缩', '蜷缩'],'敲声': ['浊响', '沉闷', '浊响', '沉闷', '浊响', '浊响', '浊响', '浊响', '沉闷', '清脆', '清脆', '浊响', '浊响', '沉闷', '浊响', '浊响', '沉闷'],'纹理': ['清晰', '清晰', '清晰', '清晰', '清晰', '清晰', '稍糊', '清晰', '稍糊', '清晰', '模糊', '模糊', '稍糊', '稍糊', '清晰', '模糊', '稍糊'],'脐部': ['凹陷', '凹陷', '凹陷', '凹陷', '凹陷', '稍凹', '稍凹', '稍凹', '稍凹', '平坦', '平坦', '平坦', '凹陷', '凹陷', '稍凹', '平坦', '稍凹'],'触感': ['硬滑', '硬滑', '硬滑', '硬滑', '硬滑', '软粘', '软粘', '硬滑', '硬滑', '软粘', '软粘', '硬滑', '软粘', '硬滑', '软粘', '硬滑', '硬滑'],'密度': [0.697, 0.774, 0.634, 0.608, 0.556, 0.403, 0.481, 0.437, 0.666, 0.243, 0.245, 0.343, 0.639, 0.657, 0.360, 0.593, 0.719],'含糖率': [0.460, 0.376, 0.264, 0.318, 0.215, 0.237, 0.149, 0.211, 0.091, 0.267, 0.057, 0.099, 0.161, 0.198, 0.370, 0.042, 0.103],'好瓜': ['是', '是', '是', '是', '是', '是', '是', '是', '否', '否', '否', '否', '否', '否', '否', '否', '否']
}
df = pd.DataFrame(data)# 定义离散和连续特征列名
discrete_cols = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']
continuous_cols = ['密度', '含糖率']
target_col = '好瓜'# 2. 训练模型
# 计算先验概率 P(y)
prior_prob = df[target_col].value_counts(normalize=True).to_dict()# 计算离散特征的条件概率 P(xi|y) - 使用拉普拉斯平滑
cond_prob_discrete = {}
for feature in discrete_cols:cond_prob_discrete[feature] = {}# 获取该特征的所有可能取值possible_values = df[feature].unique()k = len(possible_values) for value in possible_values:cond_prob_discrete[feature][value] = {}for class_label in df[target_col].unique():# 获取目标类别的数据子集class_subset = df[df[target_col] == class_label]# 计算分子：(类别为y且特征为x的数量 + 1)count_feature_class = class_subset[class_subset[feature] == value].shape[0] + 1# 计算分母：(类别为y的数量 + k)count_class = class_subset.shape[0] + kcond_prob_discrete[feature][value][class_label] = count_feature_class / count_class# 计算连续特征的均值和标准差，按类别分组
mean_std_continuous = {}
for feature in continuous_cols:mean_std_continuous[feature] = {}for class_label in df[target_col].unique():class_subset = df[df[target_col] == class_label]# 计算均值和标准差 (使用 N-1 作为分母，即样本标准差)mean = class_subset[feature].mean()std = class_subset[feature].std()# 防止标准差为0 (如果某类下某个连续特征值都一样)if std == 0:std = 1e-6 mean_std_continuous[feature][class_label] = {'mean': mean, 'std': std}# 高斯概率密度函数
def gaussian_pdf(x, mean, std):exponent = math.exp(-((x - mean) ** 2 / (2 * std ** 2)))return (1 / (math.sqrt(2 * math.pi) * std)) * exponent# 3. 预测函数 (Prediction Function)
def predict_watermelon(test_data):scores = {}# 遍历每个类别 ('是', '否')for class_label in prior_prob.keys():# 初始化得分为该类别的先验概率 P(y)score = math.log(prior_prob[class_label])# 计算离散特征的条件概率连乘 (对数形式下为连加)for feature in discrete_cols:value = test_data[feature]if value in cond_prob_discrete[feature]:score += math.log(cond_prob_discrete[feature][value][class_label])else:score += math.log(1e-9) # 计算连续特征的高斯概率密度连乘 (对数形式下为连加)for feature in continuous_cols:x = test_data[feature]stats = mean_std_continuous[feature][class_label]pdf = gaussian_pdf(x, stats['mean'], stats['std'])if pdf > 0:score += math.log(pdf)else:score += math.log(1e-9)scores[class_label] = score# 返回得分最高的类别prediction = max(scores, key=scores.get)return prediction, scores# 4. 进行预测 
test_sample = {'色泽': '青绿','根蒂': '蜷缩','敲声': '浊响','纹理': '清晰','脐部': '凹陷','触感': '硬滑','密度': 0.697,'含糖率': 0.460
}# 调用预测函数
prediction, scores = predict_watermelon(test_sample)print(f"\n测试样本: {test_sample}")
print(f"预测结果: {prediction}")
print(f"各类别的对数得分: {scores}")

四、学习总结

通过学习，我清晰了整个朴素贝叶斯算法的运作流程：从训练数据中学习先验概率 P(y) 和所有特征的条件概率（或相关统计量）P(xi∣y)，到预测阶段将这些概率（通常是以对数形式来保证数值稳定性）组合起来，计算出每个类别的最终得分，最后基于得分比较做出分类决策。

朴素贝叶斯算法的优点在于简单高效、对小数据集表现良好、对噪声鲁棒，适合快速建模场景（如西瓜预测和垃圾邮件分类）。但其缺点也很明显：特征独立性假设不现实、对数据分布敏感、分类能力有限。针对这些缺点，可通过特征工程、分布变换或模型改进提升性能。

一、朴素贝叶斯的算法原理

1.1 定义

1.2 贝叶斯定理

1.3 条件独立性假设

二、朴素贝叶斯算法的几种常见类型

2.1 高斯朴素贝叶斯 (Gaussian Naive Bayes)

【训练阶段】 - 从数据中学习模型参数

【预测阶段】 - 对新样本 Xnew​ 进行分类

2. 2 多项式朴素贝叶斯 (Multinomial Naive Bayes)

【训练阶段】 - 学习模型参数

【预测阶段】 - 对新样本 Xnew​ 进行分类

2.3 伯努利朴素贝叶斯 (Bernoulli Naive Bayes)

【训练阶段】 - 学习模型参数

【预测阶段】 - 对新样本 Xnew​ 进行分类

三、实例：基于朴素贝叶斯的好瓜预测

任务： 对一个给定的西瓜样本进行二分类（好瓜/坏瓜）

1.训练数据

2.测试数据

3.计算步骤

4.代码实现

四、学习总结

相关文章：

【预测阶段】 - 对新样本 Xnew 进行分类

【预测阶段】 - 对新样本 Xnew 进行分类

【预测阶段】 - 对新样本 Xnew 进行分类

任务：对一个给定的西瓜样本进行二分类（好瓜/坏瓜）