当前位置：首页 > news >正文

【优选算法-二分查找】二分查找算法解析：如何通过二段性优化搜索效率

news 来源：原创 2025/5/30 18:51:19

在这里插入图片描述

算法	相关知识点	可以通过点击	以下链接进行学习	一起加油！
双指针	滑动窗口

在本篇文章中，我们将深入解析二分查找算法的核心原理。从基本概念到实际应用，带你了解如何利用二分查找高效定位元素，提升搜索效率。无论你是刚接触算法的新手，还是想优化代码性能的老手，二分查找都是你不可忽视的强大工具！

请添加图片描述

Alt

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\ C++
🌈初/高阶数据结构专栏：初阶数据结构\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志我自踏雪至山巅请添加图片描述

文章目录

- 34. 在排序数组中查找元素的第一个和最后一个位置(重要)
- 二段性(重要/必备知识)
- - 1.查找左端点
  - 2.循环判断条件
  - 3. left和right移动方式
  - 3.求中点操作
  - 4.总结二分模板
- 69.x 的平方根
- 35.搜索插入位置
- 69.山脉数组的峰顶索引
- 162. 寻找峰值
- 153. 寻找旋转排序数组中的最小值
- LCR 173. 点名

34. 在排序数组中查找元素的第一个和最后一个位置(重要)

【题目】：34. 在排序数组中查找元素的第一个和最后一个位置

在这里插入图片描述

如果题目为"在排序数组中查找元素"，很自然可以想到朴素二分查找，根据中间数值讨论，但是"朴素二分"不适合更有层度题目，比如说这道题目。

首先如果使用朴素二分单凭一个中间值，很难得知第一个和最后一个位置。如果出现全部是相同元素的情况，会导致时间复杂度降成同暴力解法般，对此我们应该借助"二段性"优化二分查找策略

【算法思路】

二段性(重要/必备知识)

在二分查找算法中，“二段性”通常指的是数组被分成两个部分进行查找，每次都根据某种条件进行判断、决定在哪一部分继续搜索。简单来说，二分查找通过将问题逐步缩小到两个子问题中的一个，从而高效地找到目标元素。

1.查找左端点

通过绘图分析数组中的元素与目标值（target）之间的关系，我们可以将数组划分为两部分：左侧部分包含所有小于目标值的元素，右侧部分则包含所有大于或等于目标值的元素。这一划分是基于二分性质进行的。

在这里插入图片描述

【细节处理】

关于这部分细节，属于二分查找容易导致死循环的问题所在。

2.循环判断条件

这里有两种循环判断条件，必须要选择第一种，而不是第二种。如果选择第二种会导致死循环。

第一种：while(left < right)

第二种：while(left <= right)

选择第一种理由

【理由一】：

这里只能选择第一种while(left < right)，否则就会死循环。比如left = mid 或者 right = mid，当你判断条件为left <= right，left == right 一直为真，导致死循环

【理由二】：

left ==right的时候，就是最终结构，无需判断。图中有三种情况佐证：有结果，全大于t，全小于t

在这里插入图片描述

3. left和right移动方式

通过二分法将数组划分为两部分。在此过程中，需要根据目标值与当前划分区域的关系来判断left和right的移动方式。

在这里插入图片描述

通过绘图分析，如果目标值位于左侧且mid落在左侧，则left应设置为mid，而不是mid + 1，以避免错过目标值；如果mid落在右侧，则由于目标值不在右侧，right应设置为mid - 1

同理可得，当目标位于右侧，如果mid落在右侧，则right应设置为mid，而不是mid - 1，以避免错过目标值；如果mid落在左侧，则left应设置为mid + 1，因为目标值不在左侧。

3.求中点操作

首先考虑到 right 可能会超过Max值，所以会先采用 left + (right - left) / 2。在二分查找中，求中点操作有两个方式，在不同场景选择适合的方式，否则容易导致死循环

在这里插入图片描述

【第一种方式】: mid = left + (right - left) / 2，会导致mid落在左侧

【第二种方式】:mid = left + (right - left + 1) / 2，会导致mid落在右侧

例如，求左端点时，如果left = mid，right = mid - 1，根据这两个变量的移动规律，若使用第一种方式（left = mid + 1），会导致死循环，因此应使用第二种方式（left = mid）。同理，求右端点时，若left = mid + 1，right = mid，应根据相应的规则调整边界，避免死循环并确保正确找到右端点，选择第一种方式。

【代码实现】

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;int begin = 0;if(nums.size() == 0) return {-1,-1};//求解左端点while(left < right){int mid = left + (right - left)/2;if(nums[mid] < target) left = mid + 1;else right = mid;}if(target != nums[left]) return {-1,-1};else begin = left;left = 0,right = nums.size() - 1;//求解右端点while(left < right){int mid = left + (right - left + 1)/2;if(nums[mid] > target) right = mid - 1;else left = mid;}return {begin,left};}
};

4.总结二分模板

在这里插入图片描述

通过不断刷题，我们会发现很多题目都是相似的。如果忘记了某些常用模板，也可以通过上述方式重新推导。关键在于如何识别题目中的二分性质，从而将问题划分为两个区间。

69.x 的平方根

【题目】：69. x 的平方根

在这里插入图片描述

【算法思路】

1.暴力查找

通过枚举从 0 到 x 之间的每个整数 i，判断是否满足条件：

这里不需要考虑是否枚举到 x / 2 或 x / 2 + 1，因为一旦找到结果就直接返回，后续的情况不再进行判断。过多的区间研究不仅浪费时间，还容易出错。

如果 i * i == x，直接返回 i；
如果 i * i > x，说明前一个数 i-1 的平方已经超过了 x，因此返回 i - 1。

由于 i * i 可能会超过 int 的最大值，所以应使用 long long 类型来存储变量。

class Solution {
public:int mySqrt(int x) {// 使用 long long 来避免溢出long long i = 0;for (i = 0; i <= x; i++) {// 如果平方等于 x，返回 iif (i * i == x) return i;// 如果平方大于 x，返回 i - 1if (i * i > x) return i - 1;}// 为了确保所有路径有返回值return -1;}
};

2.二分查找

在这里插入图片描述

设x的平分根的最终结果为ret。分析ret左右两侧数据的特点，从而发现二段性。

在这里插入图片描述

【代码实现】

class Solution {
public:int mySqrt(int x){int left = 1, right = x;if(x < 1) return 0;//处理下边界情况while(left < right){long long mid = left + (right - left + 1)/2;if(mid * mid <= x) left = mid;else right = mid - 1;}return left;}
};

35.搜索插入位置

【题目】：35. 搜索插入位置

在这里插入图片描述

插入位置是第一个大于目标值的数，或者是最后一个数据。如果当前的数大于或等于目标值，那么这里就是我们所需的二分区间。如果没有元素，在最后一个位置，特殊情况特殊处理。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

【代码实现】

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while(left < right){int mid = left + (right - left)/2;if(nums[mid] < target) left = mid +1 ;else right = mid;}if(nums[left] < target) return right + 1;else return right;}
};

这里需要判断下，如果达到最后一个位置情况(nums[left] < target。

69.山脉数组的峰顶索引

【题目】：69. 山脉数组的峰顶索引

在这里插入图片描述

【算法思路】

在这里插入图片描述

通过绘图分析元素之间的大小关系，从而确定二分法的划分区间。

【代码实现】

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left = 0, right = arr.size()-1;while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid - 1] <= arr[mid]) left = mid;else right = mid - 1;}return left;}
};

【细节分析】

1.arr[mid - 1] <= arr[mid] 是否会越界？

在 arr[mid - 1] 中，mid 的最小值是 1，因为 mid = left + (right - left + 1) / 2，而 left 从 0 开始，mid 永远不会是 0。arr[mid - 1] 访问的是 mid 左边的元素，因此不会越界。

2.如果采用arr[mid + 1]后果

如果是 arr[mid + 1]，那会导致在 mid 达到数组最后一个元素时越界，但是这种情况在这个算法中并没有发生，因为我们始终是在 left 到 right 的范围内进行查找，确保 mid + 1 不会超出界限。

162. 寻找峰值

【题目】：162. 寻找峰值

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

解法一：暴力解法

在这里插入图片描述

解法二：滑动窗口

通过两个点的分析，如果arr[i]>arr[i+1]，呈现下降趋势，可以判断左边一定有峰值，但是右边不一定有峰值，可能是直接到负无穷或者另起一峰。同理arr[i]<arr[i+1]，呈现上升趋势，可以判断右边一定有峰值，但是左边不一定有峰值。

在这里插入图片描述

我们可以根据1，2种情况去分出二段性，就可以使用二分查找。

在这里插入图片描述

如果arr[mid] > arr[mid+1]，则左侧一定有我们的结果，只需right等于mid，而arr[mid] < arr[mid+1]，则右侧一定有我们的结果，left等于mid +1去查找。

【代码实现】

class Solution {
public:int findPeakElement(vector<int>& nums){int left = 0,rigth = nums.size() - 1;while(left < rigth){int mid = left + (rigth - left + 1)/2;if(nums[mid - 1] < nums[mid]) left = mid;else rigth = mid - 1;}return left;}
};

【个人思考】

关于left和right移动规律，需要通过绘图去分析走向。这里很好通过表示了目标值是否存在作为突破口，发现二段性。所以具体情况还是需要具体分析的。

153. 寻找旋转排序数组中的最小值

【题目】：153. 寻找旋转排序数组中的最小值

在这里插入图片描述

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

解法一：暴力解法

暴力查找最小值，时间复杂度O(N)。暴力解法慢，是没有利用这个数组的特性，经过旋转的有序数组。

解法二：二分查看

画张曲线图，寻找二段性，以D点nums[n-1]为参照物，AB区域是严格大于D点，CD区域是小于等于D点的。

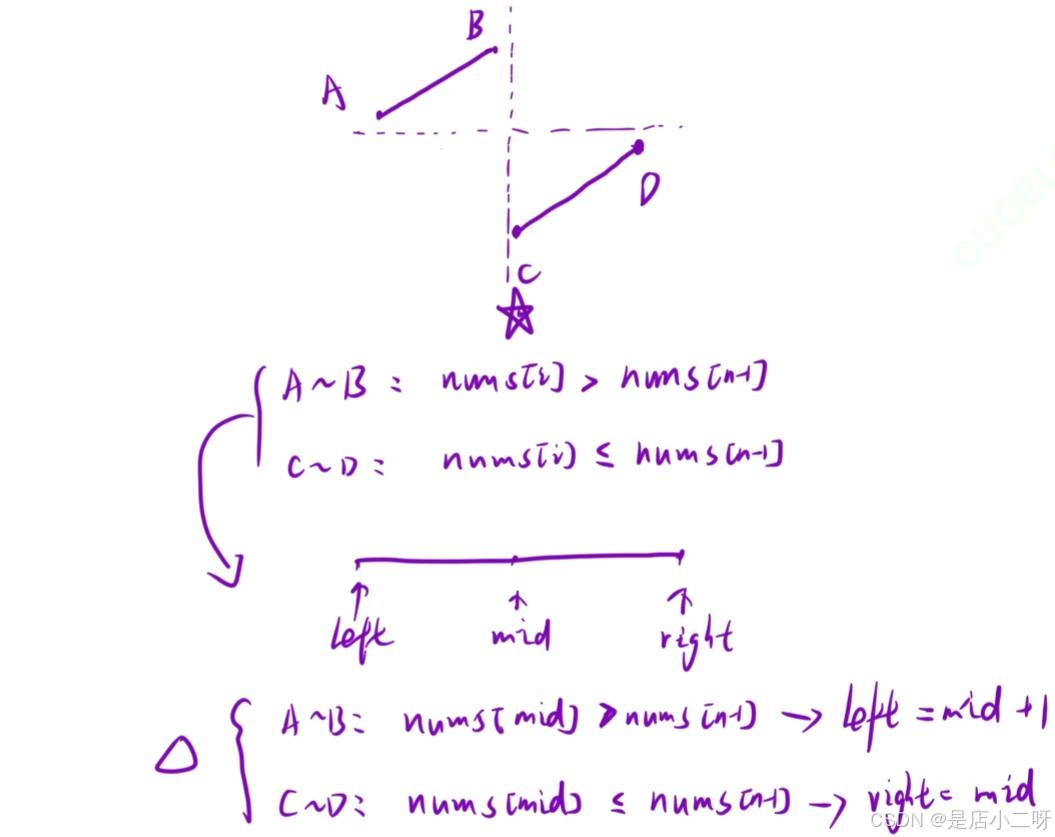
在这里插入图片描述

通过mid在某个区间如何移动，去推到两个变量的移动方式。

【代码实现】

class Solution {
public:int findMin(vector<int>& nums) {int left = 0,right = nums.size() - 1;int x =nums[right];while(left < right){int mid = left + (right - left)/2;if(nums[mid] > x) left = mid + 1;else right = mid;}return nums[left];}
};

【疑问:选择A点的值作为参照物】

那么x = nums[0]，通过绘图和mid落点去推导left和right移动方式即可。

LCR 173. 点名

【题目】：LCR 173. 点名

在这里插入图片描述

1.常见解法

哈希表法
创建一个大小为 n+1 的哈希表，遍历原始数组并将元素填入哈希表，然后检查哪个位置没有被填充，这就是缺失的数字。
直接遍历法
直接遍历原数组，找到缺失的元素。
位运算法 (XOR)
使用位运算（XOR）来抵消重复出现的数字，最终剩下的就是缺失的数字。
数学法 (高斯求和公式)
利用等差数列的求和公式，计算从 0 到 n 的总和与数组中所有元素的和之间的差值，得出缺失的数字。

这些方法的时间复杂度都是 O(n)，因此适合处理大规模数据。

2.二分查找

【思考：0 到 n-1，为什么长度是 n-1？这个问题常见于面试中，面试官可能会与你探讨是否还有其他解法。】

这里可以根据图下，发现二段性使用二分查找。

在这里插入图片描述

通过比较数值与对应下标的关系，作为二分法的判定标准，从而划分搜索区间。

class Solution {
public:int takeAttendance(vector<int>& records) {int left = 0,rigth = records.size() - 1;while(left < rigth){int mid = left + (rigth - left) / 2;if(records[mid] == mid) left = mid + 1;else rigth = mid;}if(records[left] == left) return left + 1;else return left;}
};

在这里插入图片描述
快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！

文章目录

34. 在排序数组中查找元素的第一个和最后一个位置(重要)

二段性(重要/必备知识)

1.查找左端点

2.循环判断条件

3. left和right移动方式

3.求中点操作

4.总结二分模板

69.x 的平方根

35.搜索插入位置

69.山脉数组的峰顶索引

162. 寻找峰值

153. 寻找旋转排序数组中的最小值

LCR 173. 点名

相关文章：