无人船 | 图解基于LQR控制的路径跟踪算法(以全驱动无人艇WAMV为例)
目录
- 1 最优控制线性二次型问题
- 2 LQR的价值迭代推导
- 3 基于全驱动无人船动力学的LQR
- 4 跟踪效果分析
1 最优控制线性二次型问题
最优控制理论是一种数学和工程领域的理论,旨在寻找如何使系统在给定约束条件下达到最佳性能的方法。它的基本思想是通过选择合适的控制输入,以最小化或最大化某个性能指标来优化系统的行为。其中,系统的动态行为通常用状态方程描述,状态表示系统在某一时刻的内部状态。状态空间表示将系统的状态和控制输入表示为向量,通常用微分方程或差分方程来描述系统的演化。在最优控制理论中,会设置代价函数或者目标函数,用来衡量系统行为的好坏的函数。性能指标可以是各种形式,如最小化路径长度、最小化能量消耗、最大化系统稳定性等。最优控制理论在许多领域都有广泛的应用,包括航空航天、机器人学、经济学、生态学等。
若系统动力学特性可以用一组线性微分方程表示,且性能指标为状态变量和控制变量的二次型函数,则此类最优控制问题称为线性二次型问题。线性二次调节器(Linear Quadratic Regulator, LQR)是求解线性二次型问题常用的求解方法之一,其假设系统零输入且期望状态为零。

如图所示的全状态反馈控制系统。设控制误差 x k = z k − z k ∗ \boldsymbol{x}_k=\boldsymbol{z}_k-\boldsymbol{z}_{k}^{*} xk=zk−zk∗,其中 z k \boldsymbol{z}_k zk、 z k ∗ \boldsymbol{z}_{k}^{*} zk∗分别是第 k k k个控制时间步的实际状态和期望状态,则全反馈控制律由误差驱动
v k = v k ∗ − K x k ⇔ u = v − v ∗ u k = − K x k \boldsymbol{v}_k=\boldsymbol{v}_{k}^{*}-\boldsymbol{Kx}_k\xLeftrightarrow{\boldsymbol{u}=\boldsymbol{v}-\boldsymbol{v}^*}\boldsymbol{u}_k=-\boldsymbol{Kx}_k vk=vk∗−Kxku=v−v∗ uk=−Kxk
上式表明可以通过选取状态变量和输入变量,使系统等效为零输入(跟踪期望输入)且期望状态为零(消除状态误差),满足应用LQR进行最优控制的条件。定义代价函数
J = ∑ k = 0 N ( x k T Q x k + u k T R u k ) J=\sum_{k=0}^N{\left( \boldsymbol{x}_{k}^{T}\boldsymbol{Qx}_k+\boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k \right)} J=k=0∑N(xkTQxk+ukTRuk)
其中 Q \boldsymbol{Q} Q与 R \boldsymbol{R} R是用户设定的半正定矩阵,前者衡量了系统状态向期望轨迹的收敛速度,后者衡量了系统能量消耗的相对大小,二者互相制约——希望系统快速收敛往往需要加强控制力度,导致能量耗散。因此, 与 需要结合具体场景进行调节。
2 LQR的价值迭代推导
针对 J J J进行优化,引入价值迭代策略,价值迭代的理论基础请看Pytorch深度强化学习1-4:策略改进定理与贝尔曼最优方程详细推导
J k ( x k , u k ) = min u k [ x k T Q x k + u k T R u k + J k + 1 ( x k + 1 ) ] J_k\left( \boldsymbol{x}_k,\boldsymbol{u}_k \right) =\underset{\boldsymbol{u}_k}{\min}\left[ \boldsymbol{x}_{k}^{T}\boldsymbol{Qx}_k+\boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k+J_{k+1}\left( \boldsymbol{x}_{k+1} \right) \right] Jk(xk,uk)=ukmin[xkTQxk+ukTRuk+Jk+1(xk+1)]
即第 k k k步到终端的代价等于当前步的代价与第 k + 1 k+1 k+1步到终端的代价之和。根据 J J J的定义,其一定能表示成二次型 J k = x k T P k x k J_k=\boldsymbol{x}_{k}^{T}\boldsymbol{P}_k\boldsymbol{x}_k Jk=xkTPkxk,对于优化问题 u k = a r g min u k J k ( x k , u k ) \boldsymbol{u}_k=\mathrm{arg}\min _{\boldsymbol{u}_k}J_k\left( \boldsymbol{x}_k,\boldsymbol{u}_k \right) uk=argminukJk(xk,uk),令
∂ J k ( x k , u k ) ∂ u k = ∂ ∂ u k ( x k T P k x k + u k T R u k + J k + 1 ( A x k + B u k ) ) = ∂ ∂ u k ( u k T R u k + ( A x k + B u k ) T P k + 1 ( A x k + B u k ) ) = 2 ( R + B T P k + 1 B ) u k + 2 B T P k + 1 A x k = 0 \begin{aligned}\frac{\partial J_k\left( \boldsymbol{x}_k,\boldsymbol{u}_k \right)}{\partial \boldsymbol{u}_k}&=\frac{\partial}{\partial \boldsymbol{u}_k}\left( \boldsymbol{x}_{k}^{T}\boldsymbol{P}_k\boldsymbol{x}_k+\boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k+J_{k+1}\left( \boldsymbol{Ax}_k+\boldsymbol{Bu}_k \right) \right) \\&=\frac{\partial}{\partial \boldsymbol{u}_k}\left( \boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k+\left( \boldsymbol{Ax}_k+\boldsymbol{Bu}_k \right) ^T\boldsymbol{P}_{k+1}\left( \boldsymbol{Ax}_k+\boldsymbol{Bu}_k \right) \right) \\&=2\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) \boldsymbol{u}_k+2\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{Ax}_k\\&=0\end{aligned} ∂uk∂Jk(xk,uk)=∂uk∂(xkTPkxk+ukTRuk+Jk+1(Axk+Buk))=∂uk∂(ukTRuk+(Axk+Buk)TPk+1(Axk+Buk))=2(R+BTPk+1B)uk+2BTPk+1Axk=0
则 u k ∗ = − ( R + B T P k + 1 B ) − 1 B T P k + 1 A x k \boldsymbol{u}_{k}^{*}=-\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) ^{-1}\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{Ax}_k uk∗=−(R+BTPk+1B)−1BTPk+1Axk,对比 u k = − K x k \boldsymbol{u}_k=-\boldsymbol{Kx}_k uk=−Kxk可得
K k = ( R + B T P k + 1 B ) − 1 B T P k + 1 A \boldsymbol{K}_k=\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) ^{-1}\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{A} Kk=(R+BTPk+1B)−1BTPk+1A
将 u k = − K x k \boldsymbol{u}_k=-\boldsymbol{Kx}_k uk=−Kxk代入 J k J_k Jk可得
J k = x k T P k x k = x k T ( Q + K k T R K k + ( A − B K k ) P k + 1 ( A − B K k ) ) x k J_k=\boldsymbol{x}_{k}^{T}\boldsymbol{P}_k\boldsymbol{x}_k=\boldsymbol{x}_{k}^{T}\left( \boldsymbol{Q}+\boldsymbol{K}_{k}^{T}\boldsymbol{RK}_k+\left( \boldsymbol{A}-\boldsymbol{BK}_k \right) \boldsymbol{P}_{k+1}\left( \boldsymbol{A}-\boldsymbol{BK}_k \right) \right) \boldsymbol{x}_k Jk=xkTPkxk=xkT(Q+KkTRKk+(A−BKk)Pk+1(A−BKk))xk
从而
P k = Q + A T P k + 1 A − A T P k + 1 B ( R + B T P k + 1 B ) − 1 B T P k + 1 A \boldsymbol{P}_k=\boldsymbol{Q}+\boldsymbol{A}^T\boldsymbol{P}_{k+1}\boldsymbol{A}-\boldsymbol{A}^T\boldsymbol{P}_{k+1}\boldsymbol{B}\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) ^{-1}\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{A} Pk=Q+ATPk+1A−ATPk+1B(R+BTPk+1B)−1BTPk+1A
称为离散迭代黎卡提方程。根据贝尔曼最优原理,在迭代过程中 P k \boldsymbol{P}_k Pk会逐步收敛。
3 基于全驱动无人船动力学的LQR
针对WAMV非线性动力学模型,首先将非线性问题线性化,得到系统线性误差状态方程。具体而言,选择状态量 x = [ l x y ψ u v r ] T \boldsymbol{x}=\left[ \begin{matrix}{l} x& y& \psi& u& v& r\\\end{matrix} \right] ^T x=[lxyψuvr]T和控制量 u = [ τ l τ m τ r ] T \boldsymbol{u}=\left[ \begin{matrix} \tau _l& \tau _m& \tau _r\\ \end{matrix} \right] ^T u=[τlτmτr]T,系统状态方程为 x ˙ = f ( x , u ) \boldsymbol{\dot{x}}=\boldsymbol{f}\left( \boldsymbol{x},\boldsymbol{u} \right) x˙=f(x,u),则令 f \boldsymbol{f} f在参考点 x r \boldsymbol{x}_r xr、 u r \boldsymbol{u}_r ur泰勒级数展开,忽略非线性项可得
x ˙ = f ( x r , u r ) + ∂ f ( x , u ) ∂ x ∣ x r , u r ( x − x r ) + ∂ f ( x , u ) ∂ u ∣ x r , u r ( u − u r ) \boldsymbol{\dot{x}}=\boldsymbol{f}\left( \boldsymbol{x}_r, \boldsymbol{u}_r \right) +\frac{\partial \boldsymbol{f}\left( \boldsymbol{x}, \boldsymbol{u} \right)}{\partial \boldsymbol{x}}\mid_{\boldsymbol{x}_r,\boldsymbol{u}_r}^{}\left( \boldsymbol{x}-\boldsymbol{x}_r \right) +\frac{\partial \boldsymbol{f}\left( \boldsymbol{x}, \boldsymbol{u} \right)}{\partial \boldsymbol{u}}\mid_{\boldsymbol{x}_r,\boldsymbol{u}_r}^{}\left( \boldsymbol{u}-\boldsymbol{u}_r \right) x˙=f(xr,ur)+∂x∂f(x,u)∣xr,ur(x−xr)+∂u∂f(x,u)∣xr,ur(u−ur)
其中雅克比矩阵
{ A = ∂ f ( x , u ) ∂ x ∣ x r , u r = [ 0 0 − u r sin ψ r − v r cos ψ r cos ψ r − sin ψ r 0 0 0 u r cos ψ r − v r sin ψ r sin ψ r cos ψ r 0 0 0 0 0 0 1 0 0 0 X u + 2 X ∣ u ∣ u ∣ u r ∣ m r r v r 0 0 0 − r r Y v / m − u r 0 0 0 0 0 N r / I z ] B = ∂ f ( x , u ) ∂ u ∣ x r , u r = [ 0 0 0 0 0 0 0 0 0 1 / m 0 1 / m 0 1 / m 0 − D / I z 0 D / I z ] \begin{cases} \boldsymbol{A}=\frac{\partial \boldsymbol{f}\left( \boldsymbol{x}, \boldsymbol{u} \right)}{\partial \boldsymbol{x}}\mid_{\boldsymbol{x}_r,\boldsymbol{u}_r}^{}=\left[ \begin{matrix} 0& 0& -u_r\sin \psi _r-v_r\cos \psi _r& \cos \psi _r& -\sin \psi _r& 0\\ 0& 0& u_r\cos \psi _r-v_r\sin \psi _r& \sin \psi _r& \cos \psi _r& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& \frac{X_u+2X_{\left| u \right|u}\left| u_r \right|}{m}& r_r& v_r\\ 0& 0& 0& -r_r& {{Y_v}/{m}}& -u_r\\ 0& 0& 0& 0& 0& {{N_r}/{I_z}}\\\end{matrix} \right]\\ \boldsymbol{B}=\frac{\partial \boldsymbol{f}\left( \boldsymbol{x}, \boldsymbol{u} \right)}{\partial \boldsymbol{u}}\mid_{\boldsymbol{x}_r,\boldsymbol{u}_r}^{}=\left[ \begin{matrix} 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ {{1}/{m}}& 0& {{1}/{m}}\\ 0& {{1}/{m}}& 0\\ {{-D}/{I_z}}& 0& {{D}/{I_z}}\\\end{matrix} \right]\\\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧A=∂x∂f(x,u)∣xr,ur=⎣⎢⎢⎢⎢⎢⎢⎡000000000000−ursinψr−vrcosψrurcosψr−vrsinψr0000cosψrsinψr0mXu+2X∣u∣u∣ur∣−rr0−sinψrcosψr0rrYv/m0001vr−urNr/Iz⎦⎥⎥⎥⎥⎥⎥⎤B=∂u∂f(x,u)∣xr,ur=⎣⎢⎢⎢⎢⎢⎢⎡0001/m0−D/Iz00001/m00001/m0D/Iz⎦⎥⎥⎥⎥⎥⎥⎤
选择状态误差量 x ~ = [ l x − x r y − y r ψ − ψ r u − u r v − v r r − r r ] T \boldsymbol{\tilde{x}}=\left[ \begin{matrix}{l} x-x_r& y-y_r& \psi -\psi _r& u-u_r& v-v_r& r-r_r\\\end{matrix} \right] ^T x~=[lx−xry−yrψ−ψru−urv−vrr−rr]T得到线性误差状态方程 x ~ ˙ = A x ~ + B u + C \boldsymbol{\dot{\tilde{x}}}=\boldsymbol{A\tilde{x}}+\boldsymbol{Bu}+\boldsymbol{C} x~˙=Ax~+Bu+C,其中 C = B u r \boldsymbol{C}=\boldsymbol{Bu}_r C=Bur是常数矩阵。为了应用标准LQR过程,暂时忽略常数 C \boldsymbol{C} C,采用采样步长为 T T T的前向欧拉法离散化上述状态方程可得
x ~ ( k + 1 ) = ( T A + I ) x ~ ( k ) + T B u ( k ) \boldsymbol{\tilde{x}}\left( k+1 \right) =\left( T\boldsymbol{A}+\boldsymbol{I} \right) \boldsymbol{\tilde{x}}\left( k \right) +T\boldsymbol{Bu}\left( k \right) x~(k+1)=(TA+I)x~(k)+TBu(k)
接着进行LQR过程即可
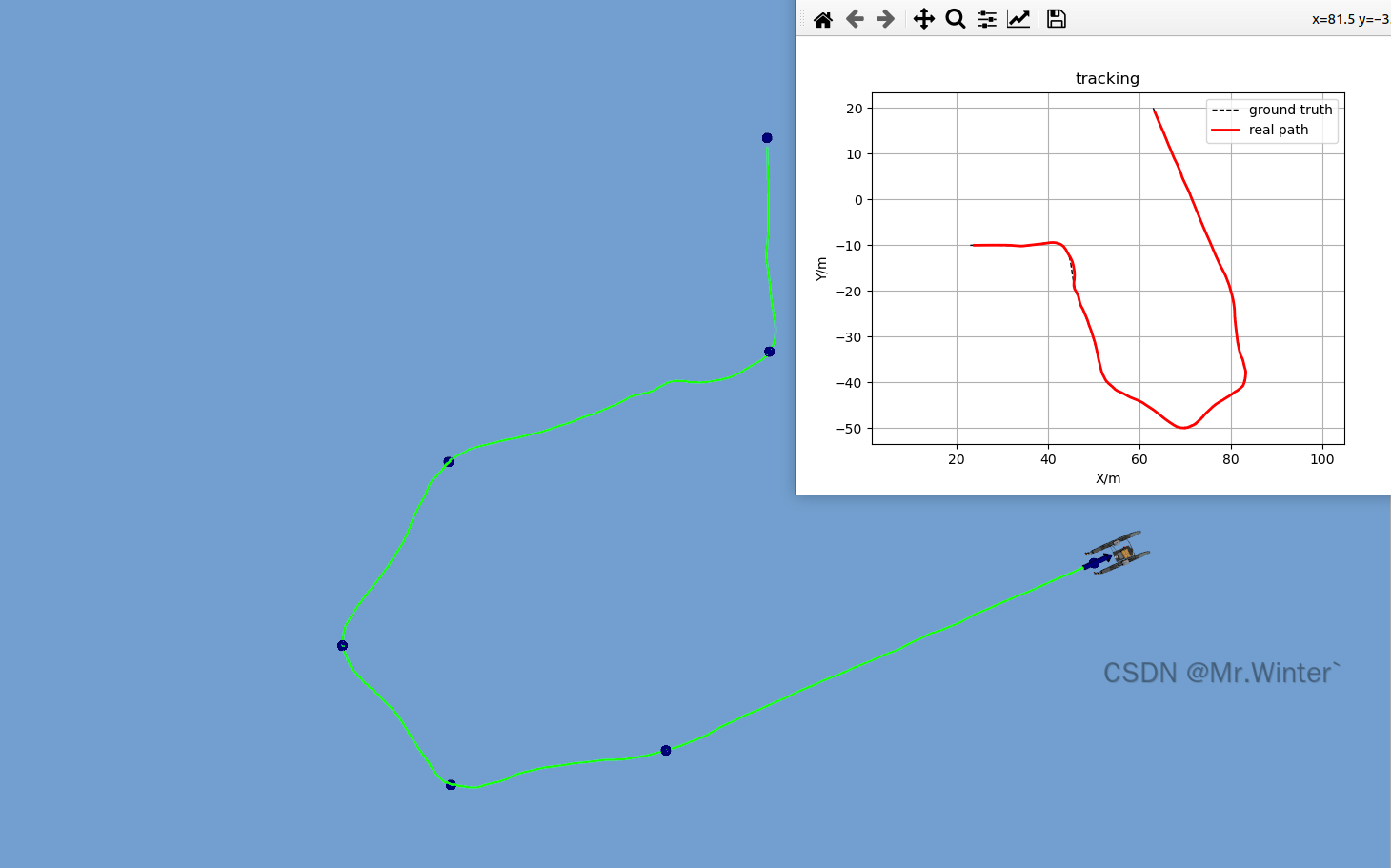
4 跟踪效果分析
定性测试结果:

在考虑水动力、风力等真实干扰的情况下,跟踪轨迹如下所示,定量测试结果为:
- 平均跟踪误差:0.188978 m
- 最大跟踪误差:0.626185 m
- 最小跟踪误差:0.006301 m
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:
)
无人船 | 图解基于LQR控制的路径跟踪算法(以全驱动无人艇WAMV为例)
目录 1 最优控制线性二次型问题2 LQR的价值迭代推导3 基于全驱动无人船动力学的LQR4 跟踪效果分析 1 最优控制线性二次型问题 最优控制理论是一种数学和工程领域的理论,旨在寻找如何使系统在给定约束条件下达到最佳性能的方法。它的基本思想是通过选择合适的控制输…...

检查IBM MQ SSL配置是否成功
使用 DISPLAY 命令检查任务是否已成功完成。 如果任务成功,那么生成的输出类似于以下示例中显示的输出。 从队列管理器 QM1,输入以下命令: DISPLAY CHS(QM1.TO.QM2) SSLPEER SSLCERTI 生成的输出类似于以下示例: DISPLAY CHSTATUS(QM1.TO.QM2) SSLPE…...

EasyRTC嵌入式音视频通信SDK智能安防与监控系统的全方位升级解决方案
一、方案背景 随着安全防范意识的提升以及物联网、人工智能技术的发展,智能安防与监控系统在各领域的应用愈发广泛。传统监控系统多以单向视频传输为主,缺乏实时交互能力。EasyRTC凭借其低延迟、高可靠的实时音视频通信技术,能为智能安防与…...

Meta 推出 WebSSL 模型:探索 AI 无语言视觉学习,纯图训练媲美 OpenAI CLIP
Web-SSL 探索了视觉自监督学习(SSL)在网络规模数据上的扩展潜力。通过调整模型大小和训练数据,我们证明了纯视觉模型可以与 CLIP 等语言监督方法相媲美,甚至超越它们,从而对 "语言监督是学习多模态建模所需的强大…...

node.js puppeteer 实践
puppeteer 介绍 Puppeteer 是 Google 推出的一个 Node.js 库,它通过 Chromium 提供了一个高效、简洁的 API,用于操作无头浏览器或具有 UI 的完整浏览器。它广泛应用于 自动化测试、数据抓取、页面性能分析和 UI 测试等领域。 Puppeteer 是一个 Node 库&…...

【现代深度学习技术】循环神经网络07:通过时间反向传播
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈PyTorch深度学习 ⌋ ⌋ ⌋ 深度学习 (DL, Deep Learning) 特指基于深层神经网络模型和方法的机器学习。它是在统计机器学习、人工神经网络等算法模型基础上,结合当代大数据和大算力的发展而发展出来的。深度学习最重…...

如何在idea中写spark程序
一、环境准备 1. 安装 IntelliJ IDEA: 下载并安装 IntelliJ IDEA(推荐使用 Community 版本,它已经支持 Scala 和 Spark 开发)。 官方下载地址:[JetBrains IntelliJ IDEA](https://www.jetbrains.com/idea/downlo…...

硬件加密+本地部署,大模型一体机如何打造AI安全护城河?
2025年,大模型技术加速渗透千行百业,但随之而来的安全风险也引发广泛关注。数据显示,近九成企业部署的大模型服务器存在“裸奔”隐患,数据泄露、模型篡改、算力劫持等问题频发。 在此背景下,大模型一体机凭借“开箱即…...

在另外一台可以科学下载的电脑用ollama下载模型后,怎么导入到另外一台服务器的ollama使用
环境: Win10专业版 Ubuntu20.04 问题描述: 在另外一台可以科学下载的电脑用ollama下载模型后,怎么导入到另外一台服务器的ollama使用,原电脑win10上的ollama下载的模型,复制到ubuntu20.04的ollama上推理 解决方案:…...

鼠标滚动字体缩放
在VsCode中编辑文件时,有时候发现Ctrl鼠标滚轮并不能缩放字体,下面是启用这个功能的方法。 第一步: 进入设置,可以从左下角按钮菜单进入,也可以使用【Ctrl,】。 第二步: 启用鼠标滚轮缩放功能 第三步&…...

什么是VR相机?VR相机的发展历史
VR相机:沉浸式体验的未来科技 VR相机,全称为虚拟现实相机,是专门用于捕捉和记录三维空间和场景的设备,能够拍摄360度全景照片和视频。通过模拟人的双眼视觉差异,利用多个镜头和传感器同时捕捉周围环境的图像ÿ…...

Java面试:Spring及Spring Cloud技术深度剖析
Spring及Spring Cloud技术深度剖析 前言 在Java开发领域,Spring框架一直是企业级应用开发的中流砥柱,而Spring Boot的出现更是极大地简化了Spring应用的开发过程。同时,Spring Cloud为构建分布式系统提供了强大的支持。本文将围绕Spring及S…...

论文阅读_Search-R1_大模型+搜索引擎
英文名称:Search-R1: Training LLMs to Reason and Leverage Search Engines with Reinforcement Learning 中文名称:Search-R1:训练大型语言模型进行推理并利用搜索引擎的强化学习 链接: http://arxiv.org/pdf/2503.09516v2 代码: https://g…...

零成本AI抠图终极指南:蓝耘元生代AIDC OS+ComfyUI实现商业级效果
引言:AI抠图革命已经到来 在数字内容创作爆炸式增长的今天,高质量的图像处理已成为刚需。无论是电商平台的商品展示、自媒体博主的封面设计,还是摄影爱好者的后期处理,抠图都是最基础也是最繁琐的工作之一。 传统抠图方式面临三…...

深入理解CSS3:Flex/Grid布局、动画与媒体查询实战指南
引言 在现代Web开发中,CSS3已经成为构建响应式、美观且高性能网站的核心技术。它不仅提供了更强大的布局系统(Flexbox和Grid),还引入了令人惊艳的动画效果和精准的媒体查询能力。本文将深入探讨这些关键技术,帮助您提…...

VLM-E2E:通过多模态驾驶员注意融合增强端到端自动驾驶——论文阅读
《VLM-E2E Enhancing End-to-End Autonomous Driving with Multimodal Driver Attention Fusion》2025年2月发表,来自香港科大广州分校、理想汽车和厦门大学的论文。 一、核心问题与动机 现有端到端(E2E)自动驾驶系统直接从传感器输入映射到…...

蓝牙BLE
1、简介 蓝牙BR/EDR和BLE是蓝牙技术的两个重要分支,它们各自具有独特的特点和应用场景。 1.1、蓝牙BR/EDR 蓝牙BR(Basic Rate) 定义:蓝牙技术的首个开发版本,采用高斯频移键控(GFSK)调制技术…...
)
在VS2022中使用Lua与c交互(二)
一、核心交互机制:Lua 虚拟栈 Lua 与 C 的交互通过一个 虚拟栈(Stack) 完成,所有数据传递、函数调用均通过此栈实现。栈的每个元素可以是任意 Lua 类型(如数字、字符串、表、函数等)。 栈的结构与…...

论文阅读_Citrus_在医学语言模型中利用专家认知路径以支持高级医疗决策
英文名称:Citrus: Leveraging Expert Cognitive Pathways in a Medical Language Model for Advanced Medical Decision Support 中文名称:Citrus:在医学语言模型中利用专家认知路径以支持高级医疗决策 链接: http://arxiv.org/pdf/2502.18…...
)
浅谈PCB传输线(一)
前言:浅谈传输线的类型,以及传输线的一些行为特性。 1.传输线的种类 2.互连线被视为传输线的场景 3.传输线的行为特性*** 1.传输线的种类 PCB 中的信号传输线通常有两种基本类型: 微带线和带状线。此外,还有第三种类型–共面线(没有参考平面…...
)
Spring-全面详解(学习总结)
一:概述 1.1 为什么学 解决了两个主要问题 1. 2 学什么 1.3 怎么学 二:系统架构 作用:web开发、微服务开发、分布式系统开发 容器:用于管理对象 AOP:面向切面编程(不惊动原始程序下对其进行加强) 事…...

突破JVM边界:类加载三重门与栈帧的生存法则
类加载子系统 文件验证阶段 类加载子系统在加载Class文件时,首先会验证文件格式规范,检查文件开头的魔数标识,确保这是一个合法的JVM字节码文件。 职责边界 该子系统仅负责将Class文件加载到内存中,并不关心后续能否成功执行—…...

VSCode 查看文件的本地修改历史
1. 使用时间线视图(Timeline) 新版 VSCode 内置了一个叫 Timeline(时间线) 的功能,可以查看: 本地文件修改记录(包括保存历史)Git 提交历史(如果仓库是 Git 管理的&…...

在QGraphicsView中精确地以鼠标为锚缩放图片
在pyqt中以鼠标所在位置为锚点缩放图片-CSDN博客中的第一个示例中,通过简单设置: self.setTransformationAnchor(QGraphicsView.AnchorUnderMouse) 使得QGraphicsView具有了以鼠标为锚进行缩放的功能。但是,其内部应当是利用了滚动条的移动来…...

【Python数据驱动决策】数据分析与可视化全流程实战指南
目录 前言技术背景与价值当前技术痛点解决方案概述目标读者说明一、技术原理剖析核心概念图解核心作用讲解关键技术模块说明技术选型对比二、实战演示环境配置要求核心代码实现案例1:销售数据清洗案例2:月度销售趋势分析案例3:产品关联分析(热力图)运行结果验证三、性能对…...

报错解决:ModuleNotFoundError: No module named ‘triton.ops‘
报错原因:2024.5.21之后, triton.ops 被移动到另一个工程 triton-lang/kernels中。 参考链接:官方解释 解决方案:换用2024.5.21之前发布的版本。 pip3 install triton2.3.0...

相机-IMU联合标定:相机-IMU外参标定
文章目录 📚简介🚀标定工具kalibr🚀标定数据录制🚀相机-IMU外参标定📚简介 在 VINS(视觉惯性导航系统) 中,相机-IMU外参标定 是确保多传感器数据时空统一的核心环节,其作用可概括为以下关键点: 坐标系对齐(空间同步),外参误差会导致视觉特征点投影与IMU预积…...

Qt C++数据库实验
一、实验目的和要求 1、掌握Qt中数据库SQL类数据库的查询、插入和更新操作。 2、熟悉Qt界面设计中常用的控件。 3、了解数据库相关类。 二、实验内容 1、设计一个数据库操作软件,完成数据库的相关操作。 2、建立按钮的信号与槽函数,实现点击按钮进…...

相机-IMU联合标定:IMU标定
文章目录 📚 简介🚀标定工具安装📌 IMU标定工具 code_utils📌 IMU标定工具 imu_utils:🚀标定数据录制🚀IMU标定📚 简介 在 VINS(Visual-Inertial Navigation System,视觉惯性导航系统) 中,IMU标定 是确保系统高精度运行的关键环节。IMU(惯性测量单元)本身…...

榕壹云信用租赁系统:基于ThinkPHP+MySQL+UniApp的全链路免押租赁解决方案
信用租赁时代的全流程数字化革新 随着共享经济与信用体系的深度融合,传统租赁行业正面临效率与信任的双重挑战。榕壹云信用租赁系统依托ThinkPHP高性能框架、MySQL数据库与UniApp跨平台开发技术,构建了一套覆盖设备租赁全生命周期的数字化解决方案。通过整合多因子身份认证、…...

C语言中的指针详解
指针是C语言中非常强大且复杂的特性之一,它为我们提供了更灵活的内存管理方式,使得程序能够直接操作内存,提升效率和性能。尽管指针非常强大,但如果不理解它的概念和使用方式,很容易出现错误。因此,理解指针…...

NIPS2021 | 视觉 Transformer 的有趣特性
Intriguing Properties of Vision Transformers 摘要-Abstract引言-Introduction相关工作-Related Work视觉Transformer的有趣特性-Intriguing Properties of Vision Transformers视觉Transformer对遮挡具有鲁棒性吗?-Are Vision Transformers Robust to Occlusions…...
)
贪心算法-2208.将数组和减半的最小操作数-力扣(LeetCode)
一、题目解析 这里要注意恰好这个字眼,说明对任意数减小一半是不需要向上取整的,所以我们需要定义double类型的数据。 二、算法解析 我们需要将数组和减小为一半的次数最少,所以根据贪心算法,我们需要取数组中最大的数进行减半操…...

如何搭建spark yarn 模式的集群集群。
下载 App 如何搭建spark yarn 模式的集群集群。 搭建Spark on YARN集群的详细步骤 Spark on YARN模式允许Spark作业在Hadoop YARN资源管理器上运行,利用YARN进行资源调度。以下是搭建步骤: 一、前提条件 已安装并配置好的Hadoop集群(包括HDF…...

嵌入式开发面试典型编程题解析:排序算法、指针操作、字符处理、递归原理等基础原理的深度解析。
在嵌入式开发面试中,编程题是常见的考察形式,旨在检验求职者对基础编程知识的掌握和应用能力。以下是几道典型的嵌入式面试编程题及详细解析,帮助新手逐步理解和掌握相关知识点。 一、用交换法对学生成绩降序排序 题目描述 在嵌入式系统开…...

DeepSeek+即梦:AI视频创作从0到1全突破
目录 一、开启 AI 视频创作大门:前期准备1.1 注册与登录1.2 熟悉工具界面1.3 硬件与网络要求 二、用 DeepSeek 构思视频脚本2.1 明确创作主题与目标2.2 编写优质提示词2.3 生成并优化脚本 三、即梦 AI 实现画面生成3.1 文生图基础操作3.2 调整参数提升画质3.3 保持人…...

npm init、换源问题踩坑
文章目录 一、 问题复现二、问题解决 一、 问题复现 成功安装nodejs 以及 npm 版本如下: > node -v > v20.18.0 > npm -v > 10.8.2使用 npm init 命令时延时过长,考虑换源,使用指令 npm config set registry https://registr…...

TRex 控制台命令解析
TRex 是一种高性能的网络测试工具,用于生成和分析网络流量。以下是对这些命令的简要解释: 一、help Console Commands(控制台命令) capture:管理 PCAP 捕获。debug:用于开发的内部调试器。events&#x…...

【Shell 脚本入门】轻松上手的实战指南
🌈 个人主页:Zfox_ 🔥 系列专栏:Shell脚本编程 目录 一:🔥 什么是 Shell 🦋 常见的 Shell 类型 二:🔥 什么是 Shell 脚本 🦋 Shell 脚本规则🦋 第…...

数据结构*栈
栈 什么是栈 这里的栈与我们之前常说的栈是不同的。之前我们说的栈是内存栈,它是JVM内存的一部分,用于存储局部变量、方法调用信息等。每个线程都有自己独立的栈空间,当线程启动时,栈就会被创建;线程结束,…...
持续更新中....)
零基础制作Freertos智能小车(教程非常简易)持续更新中....
从现开始,将陆续推出各类简单的DIY电子设计,由简入深,将自己的制作过程全部分享出来,巩固自己知识的同时希望借此机会认识更多喜欢电子设计的小伙伴。 本次小车的主控芯片采用stm32f103c8t6,主要是便宜好用&am…...

Leetcode - 双周赛155
目录 一,3527. 找到最常见的回答二,3528. 单位转换 I三,3529. 统计水平子串和垂直子串重叠格子的数目四,3530. 有向无环图中合法拓扑排序的最大利润 一,3527. 找到最常见的回答 题目列表 本题是一道模拟题࿰…...

详解RabbitMQ工作模式之工作队列模式
目录 工作队列模式 概念 特点 应用场景 工作原理 注意事项 代码案例 引入依赖 常量类 编写生产者代码 编写消费者1代码 编写消费者2代码 先运行生产者,后运行消费者 先运行消费者,后运行生产者 工作队列模式 概念 在工作队列模式中&#x…...

QGIS+mcp的安装和使用
QGISmcp的安装和使用 安装qgis_mcp 下载qgis_mcp: git clone https://github.com/jjsantos01/qgis_mcp.git安装uv uv是一个由Rust语言编写的python包管理工具,旨在提供比传统工具(如 pip)更高效的依赖管理和虚拟环境操作。 p…...

Java基础361问第16问——枚举为什么导致空指针?
我们看一段代码 public enum Color {RED, BLUE, YELLOW;public static Color parse(String color) {return null;} }public static void main() {Color color Color.parse("");// 极具迷惑性,大家日常开发肯定这么写过switch (color) {case RED:break;c…...

在 C# .NET 中驾驭 JSON:使用 Newtonsoft.Json 进行解析与 POST 请求实战
JSON (JavaScript Object Notation) 已经成为现代 Web 应用和服务之间数据交换的通用语言。无论你是开发后端 API、与第三方服务集成,还是处理配置文件,都绕不开 JSON 的解析与生成。在 C# .NET 世界里,处理 JSON 有多种选择,其中…...

CentOS7——Docker部署java服务
1、安装Docker 首先要确保系统已安装 Docker,若未安装,可以参考我的另一篇文章现在CentOS7上安装Docker,文章地址如下: CentOS7系统安装Docker教程-CSDN博客 Docker当中要安装必备的软件,比如Java运行必要的JDK&#…...

Python-Part2-集合、字典与推导式
Python-Part2-集合、字典与推导式 1. set集合 ⽆序,去掉重复数据。 set1 {1,2,3,4,5,5,4,3,2,1}print(type(set1))print(set1)set2.add(66666)set2.remove(55)#不能使用下标访问set,所以修改操作一般为remove操作 add操作2.dict 字典 字典ÿ…...

《AI大模型应知应会100篇》第39篇:多模态大模型应用:文本、图像和音频的协同处理
第39篇:多模态大模型应用:文本、图像和音频的协同处理 摘要 随着人工智能技术的发展,多模态大模型(Multimodal Large Models)已经成为AI领域的热点之一。这些模型能够同时处理文本、图像、音频等多种模态数据…...

kvm学习小结
安装相关包 安装虚拟化相关包 apt install qemu-kvm qemu-system libvirt-clients libvirt-daemon-system vlan bridge-utils 安装界面相关包 apt install xinit gdmd 配置机器允许root登录 检查cpu是否支持虚拟化 egrep -o vmx|svm /proc/cpuinfo 执行命令systemctl s…...
