【C】初阶数据结构13 -- 快速排序

本篇文章主要讲解经典的排序算法 -- 快速排序算法

---

目录

1  递归版本的快速排序

1） 算法思想 

（1） hoare 版本

（2） 双指针版本

 （3） 挖坑法 

2） 代码 

3） 时间复杂度与空间复杂度分析

（1） 时间复杂度

（2） 空间复杂度

2  非递归版本的快速排序

1） 算法思想

2） 代码

3  快速排序的缺陷以及优化

1） 缺陷

2） 优化

（1） 三路划分

（2） 内省排序(IntroSort) 

4  总结

---

1  递归版本的快速排序

1） 算法思想 

  快速排序，顾名思义，就是因为该算法排序速度非常快，所以叫做快速排序算法。快速排序是分治算法的一种经典应用。快速排序利用了可以将整个大问题划分为若干个相同的子问题，然后解决子问题，大问题就随之解决的分治算法思想：

a. 假设这里排升序，首先将数组最左边那个值作为 key 值，将对整个数组进行排序划分为两部分，key 值左边的是比 key 值小的部分，key 值右边是比 key 值大的部分

b. 这样对整个数组进行排序就划分成了两个相同子问题，比 key 值小的部分进行排序与比 key 值大的部分进行排序。

  所以快速排序的关键就是某个子问题是如何解决的，下面就来讲解某个子问题是如何解决的。

  解决某个子问题的有三种算法，分别是 hoare 版本的方法，双指针法以及挖坑法。

---

（1） hoare 版本

a. 首先将每个子问题中最左边的下标定义为 left，最右边的下标定义为 right，将 left 下标定义为 keyi ，代表要进行比较的 key 值，然后让 left++

b. 如果 left 下标的值大于 key 值，那就让 left++，这样 left 就会指向比 key 值小的元素；如果 right 下标的值小于 key 值，那就让 right--，这样 right 就会指向比 key 值大的元素，然后交换他们俩，就将大的元素换到了右边，小的元素换到了左边；交换完之后，让 left++，right--

c. 循环上述过程，当循环停止时，比 key 值大的元素就会全都被交换到右边，比 key 值小的元素就会全部被交换到左边。

  那么停止条件，就是当 left > right 或者 left >= right的时候，那么具体是哪一个呢？我们来举个例子说明一下，假设对下面这些数据进行排序：

数组元素为 6 1 2 7 8 3，对这堆数据进行快速排序，达到停止条件时结果如图所示：

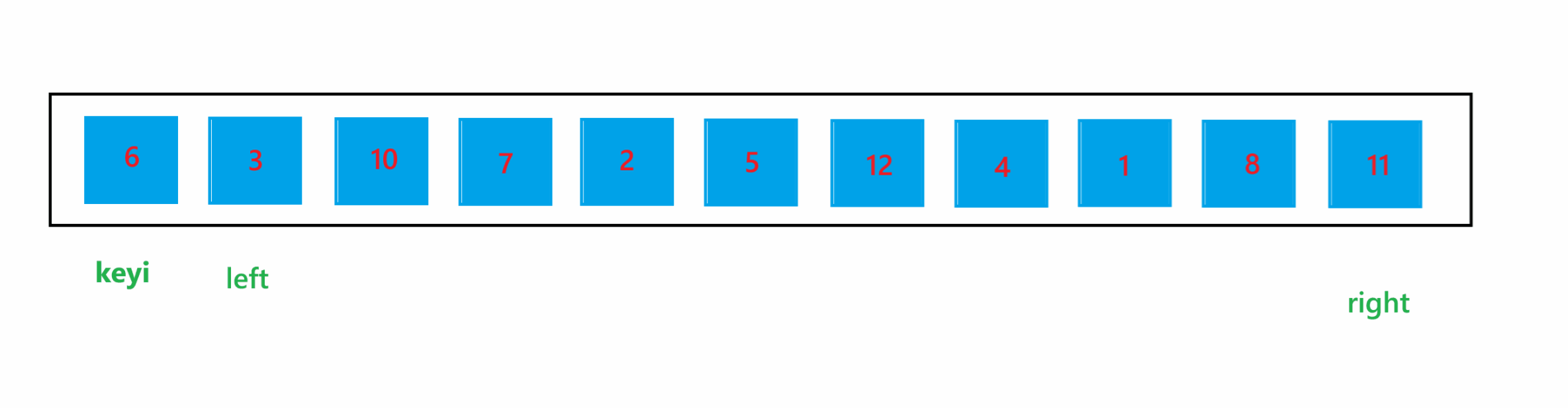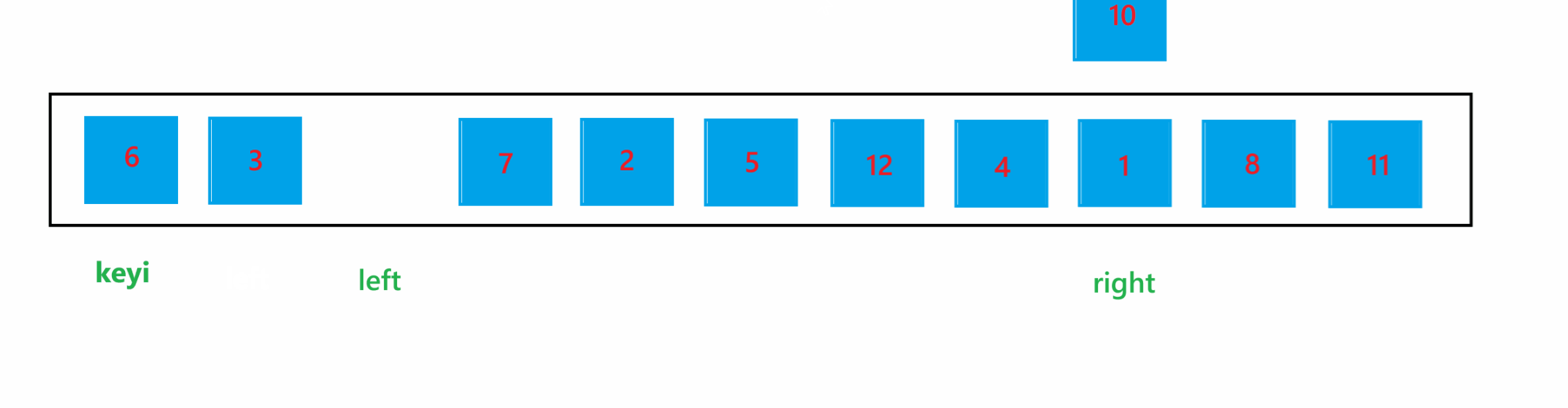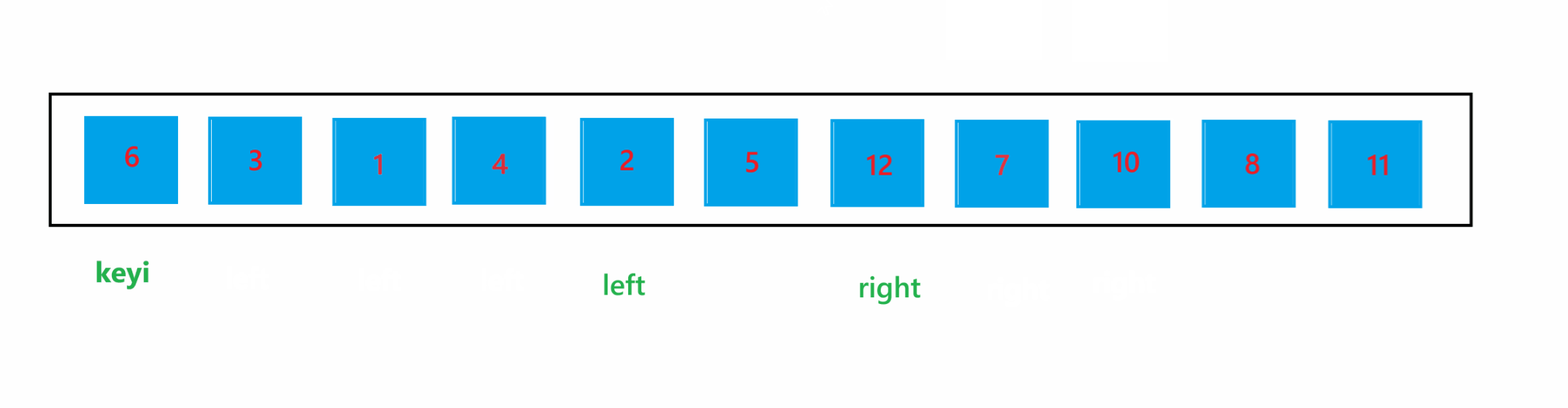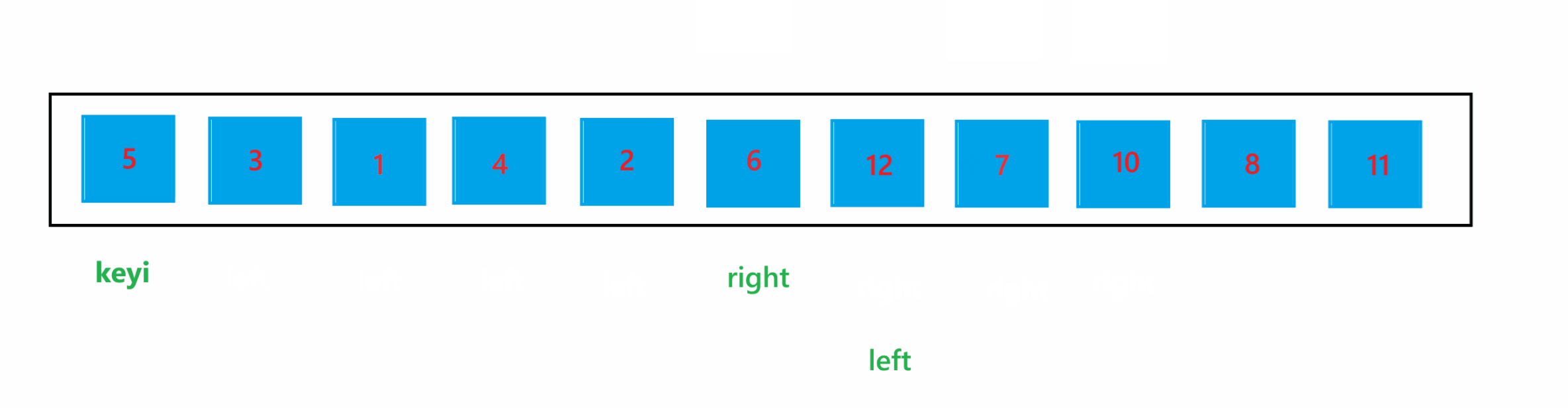
通过上图可以看到，当 left 与 right 相遇时，如果相遇的元素比 key 值大时，如果停止条件为 left >= right 的话，那循环结束之后，就会将该相遇的元素交换到 keyi 位置，那么比 key 值大的元素就被交换到左边了，肯定会导致最终结果混乱了。所以停止条件肯定是为 left > right 的，也就是进入循环的条件为 left <= right。使用 hoare 版本的一次快速排序的过程如图所示：

---

（2） 双指针版本

  在学习快速排序算法的过程中，本人认为双指针版本解决某个子问题是最好理解和代码最好写的一个版本。

a. 首先定义两个整型变量 cur 和 prev（由于这两个整型变量代表某个子问题的数组的下标，看起来像指针一样，所以是双指针版本），假设数组名是 arr，开始先让 prev  = left，是第一个元素的下标，cur 定义为 prev + 1

b. 然后 cur 在 arr 数组中遍历，如果 arr[cur] 比 arr[left] 大，那就交换 arr[++prev] 和 arr[cur]，然后让 cur++；如果 arr[cur] <= arr[left] ，那就只让 cur++

c. 当 cur > right 时，循环停止，因为如果再继续循环，就超出当前子问题数组的范围了，会导致排序结果混乱

d. 循环结束之后，不要忘记让 arr[left] 放在比 arr[left] 大的元素和 arr[left] 小的元素的分界处，即 prev 所指向位置，所以最后还要交换一下 arr[left] 和 arr[prev] 

使用双指针算法解决子问题的过程如图所示：

---

 （3） 挖坑法 

  挖坑法就是直接赋值，在挖坑法里面没有交换的操作。

a. 首先定义一个 left 变量为某个子问题最左边元素的下标，一个 right 变量为某个子问题最右边元素的下标，一个整型变量 hole 代表坑位，一个整型变量 key 代表要比较的关键值。

b. 初始定义 hole 为 left，然后让 right 找比 key 小的元素，只要 arr[right] >=  key 值，那就让 right--，找到之后，让 arr[hole] = arr[right]，然后让 hole = right，让 right 位置变为新的坑位

c. 然后让 left 找比 key 值大的元素，只要 arr[left] <= key，就让 left++，找到之后，让 arr[hole] = arr[left]，然后让 hole = left，再让 left 变为新的坑位

d. 依次执行上述过程，直到 left >= right 为止

e. 执行完上述过程之后，hole 所指向元素的左边都是比 key 值小的元素，右边都是比 key 值大的元素，最后不要忘记让 arr[hole] = key

由于每次都是将元素放到 hole 指向的位置，hole 看起来就像一个坑位，所以被形象的称为挖坑法。用挖坑法解决一次子问题的过程如图所示：

---

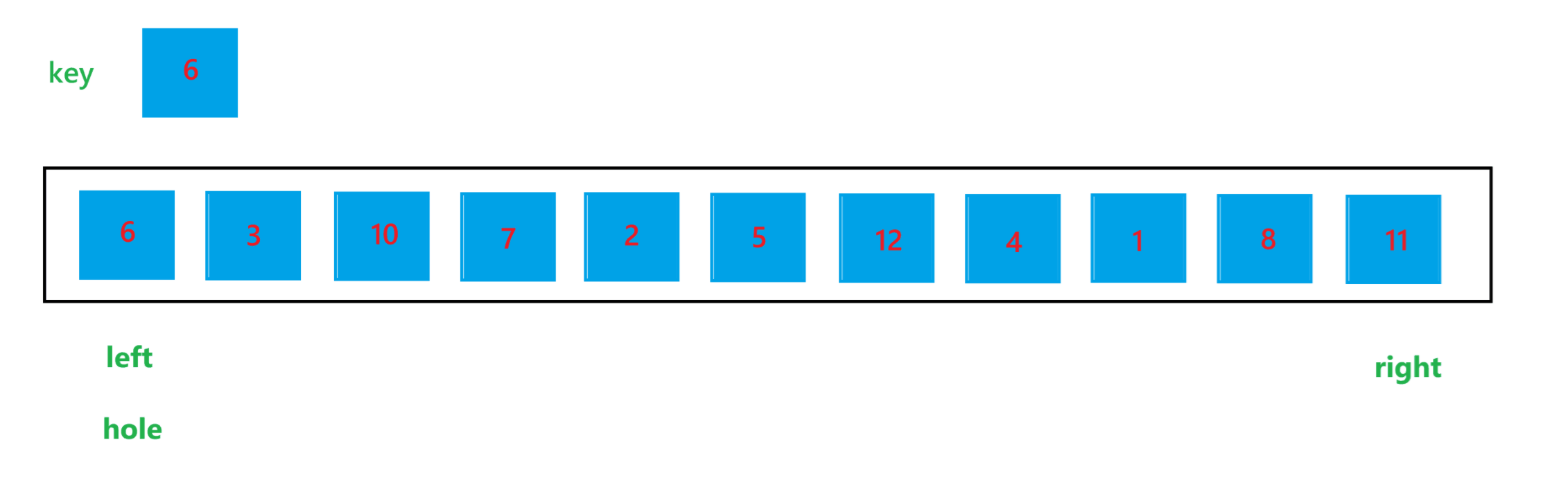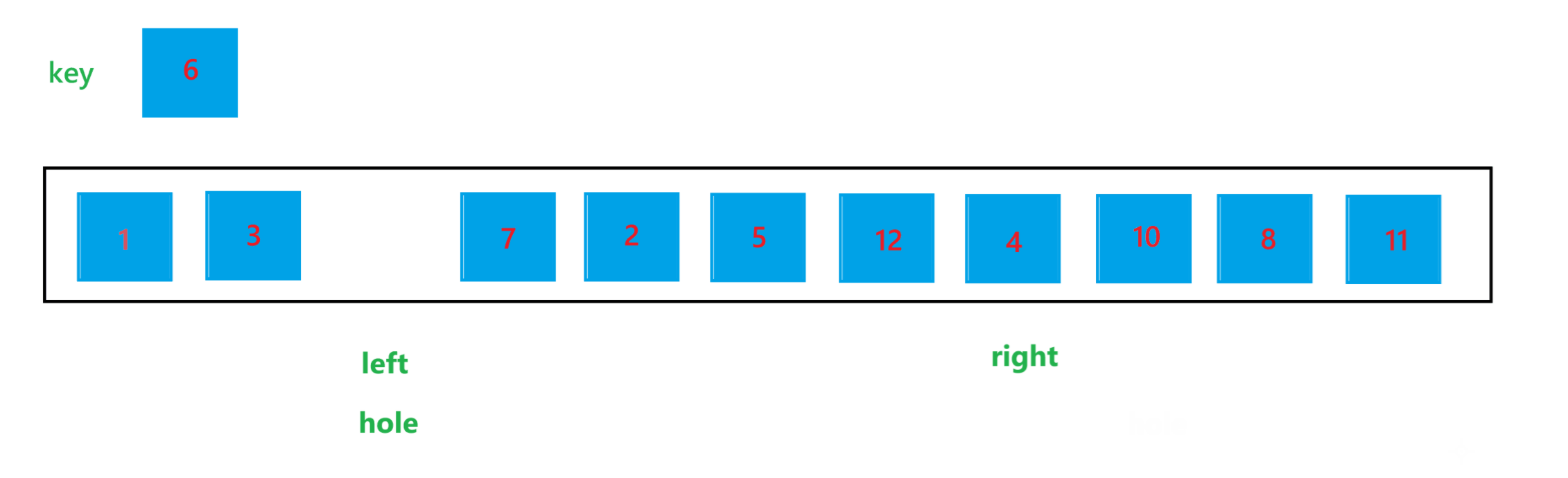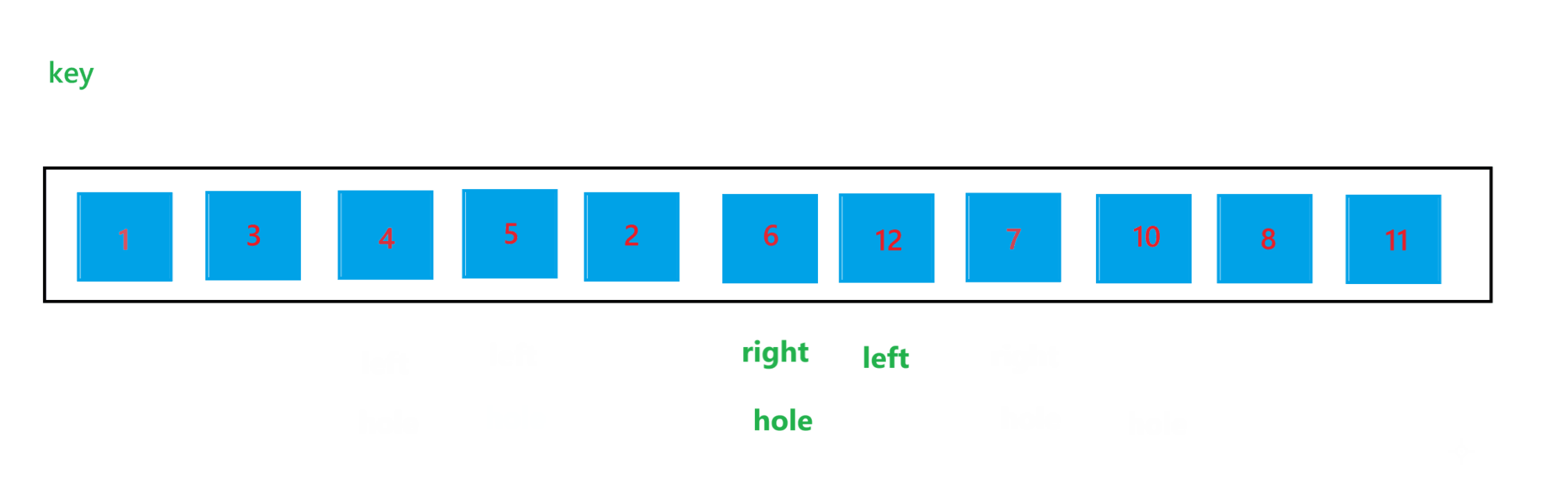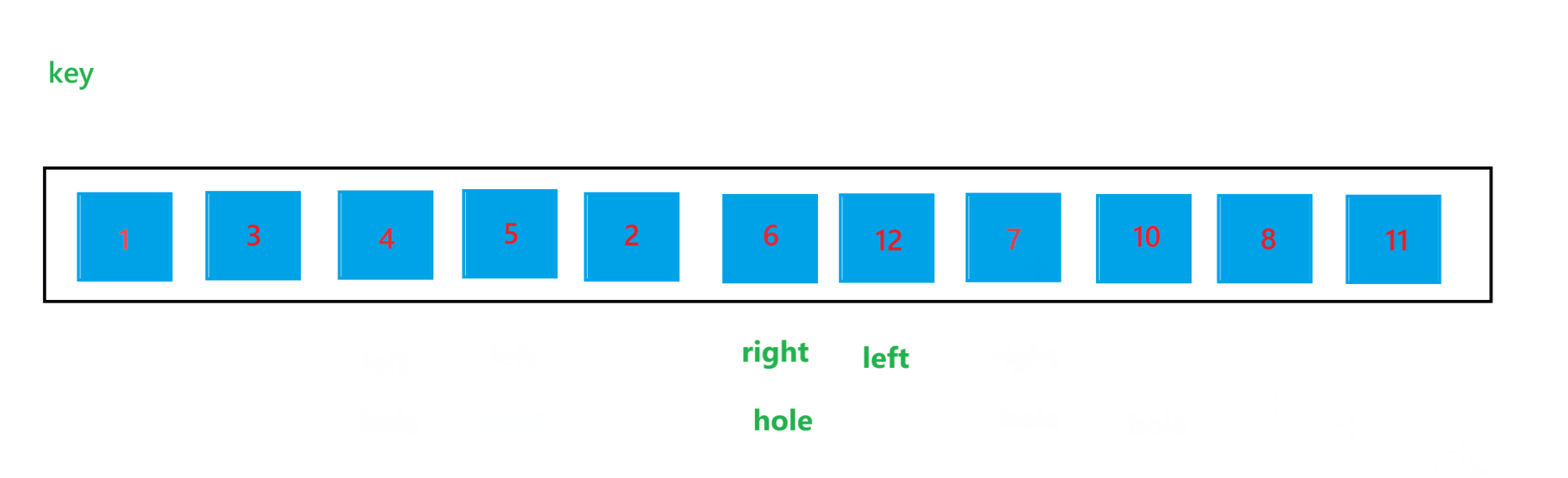
2） 代码 

快速排序主函数：

void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}int keyi = _QuickSort(arr, left, right);QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}

解决某个子问题的子函数： 

（1）  双指针法：

void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}int _QuickSort(int* arr, int left, int right)
{int prev = left, cur = prev + 1;while (cur <= right){if (arr[cur] < arr[left]){Swap(&arr[cur], &arr[++prev]);}cur++;}//把left的值放到基准值位置Swap(&arr[left], &arr[prev]);return prev;
}

（2） hoare版本：

int _QuickSort(int* arr, int left, int right)
{int keyi = left;left++;while (left <= right){//左边找大while (left <= right && arr[left] < arr[keyi])left++;//右边找小while (left <= right && arr[right] > arr[keyi])right--;if (left <= right)Swap(&arr[left++], &arr[right--]);}//再交换right与keyiSwap(&arr[right], &arr[keyi]);return right;
}

（3） 挖坑法：

int _QuickSort(int* arr, int left, int right)
{int hole = left;int key = arr[left];while (left < right){while (left < right && arr[right] >= key) right--;//找比key值小的元素arr[hole] = arr[right];hole = right;while (left < right && arr[left] <= key) left++;//找比key值大的元素arr[hole] = arr[left];hole = left;}arr[hole] = key;//最后不要忘记让坑位 = keyreturn hole;
}

 测试用例：

#include<stdio.h>
#include<stdlib.h>int main()
{int arr[10] = { 0 };//采用随机数，更加具有普遍性srand(time(NULL));int n = sizeof(arr) / sizeof(arr[0]);for (int i = 0; i < n; i++){arr[i] = rand() % (i + 1);}QuickSort(arr, 0, n - 1);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}return 0;
}

---

3） 时间复杂度与空间复杂度分析

（1） 时间复杂度

  对于具有递归函数的时间复杂度，我们总是先分析在递归过程中，解决某个子问题的函数的时间复杂度，然后乘上递归的深度，就是带有递归的函数的时间复杂度。

  首先我们先来分析解决某个子问题所使用的函数的时间复杂度。我们来看双指针版本的时间复杂度，由于仅有一层循环，最坏情况下，就是找最开始要进行排序的整个数组的 key 值，假设数组长度为 n，所以解决一个子问题的时间复杂度 T(n) = O(n)。

  再来看递归的深度，递归的深度主要是看其递归树的高度（递归树就是将其递归展开图画出来之后，其递归过程所形成的一棵树），如果不是极端情况下，每次都基本上是在中间位置对每个子问题整个数组划分为两部分，那么其递归树是一棵二叉树，且高度是  层，所以递归的深度就是 logn 级别的。

  所以快速排序的时间复杂度为 T(n) = O(nlogn)。

（2） 空间复杂度

    递归函数的空间复杂度是与递归深度有关的，因为每递归一次就会为该函数开辟一次函数栈帧，所以递归深度决定了额外使用空间的次数，在时间复杂度里，我们分析了递归深度为  次，所以空间复杂度 S(n) = O(logn) 的。

---

2  非递归版本的快速排序

1） 算法思想

  一般情况下，递归是可以与迭代（循环）相互转换的，只不过有时候使用递归比较方便，有时候使用迭代比较方便。所以，快速排序也是可以使用迭代来实现的。

  在递归版本中，我们是将对整个数组进行排序的大问题划分为对若干个子数组（数组中一段连续的区间，如大数组下标为 0~9，那么子数组的下标可以是 1~5，也可以是2~6）小问题来实现的，在迭代版本的快速排序中，我们也可以利用这一思想，但是在迭代版本中，我们是用过利用栈存储每一个子问题中子数组的左右下标来实现的：

a. 首先我们创建一个栈 st，方便后面存储下标，开始我们先让整个数组的最右边的下标 right 入栈，再让整个数组最左边的下标 left 入栈

b. 在每次循环里面，先取出栈中的第一个元素 begin ，代表某个子问题中数组的最左边的下标，然后让栈顶元素出栈

c. 再取出栈中的第二个元素 end ，代表某个子问题中数组的最右边的下标，然后让栈顶元素出栈

d. 这样就得到了要解决的子问题的数组，然后解决该子问题（这里可以使用双指针法，也可以使用挖坑法，也可使用hoare版本的方法，可以看上面的讲解）

e. 解决完子问题之后，会得到一个 key 值的下标 keyi ，之后先让 keyi - 1 入栈，再让 begin 入栈；然后再让 end 入栈，keyi + 1 入栈。

但是入栈这里有两个需要注意的点：

  （1） 在每次入栈的时候需要先让每个数组的右下边先入栈，再让左下标入栈。因为之前去栈顶元素的时候，是先取出左边下标 begin，再取出右边下标 end，遵循栈后进先出的原则，需要先入栈右边下标，再入栈左边下标。

  （2） 入栈之前，需要先做一次判断，判断右边下标是否严格大于左边下标。因为需要解决的子问题是一个子数组，当一个子问题不是一个子数组或者子数组中只有一个元素的时候，是不需要再排序的，所以右边的下标需要严格大于左边的下标。

  最后还有一个点，就是循环的结束条件。这里的结束条件也比较好想到，就是当栈不为空时，代表还有需要解决的子问题，需继续循环，当栈为空时，代表所有的子问题已经全部解决，那么整个大问题也就全部解决了，所以就不需要循环了。最后不要忘记将栈给销毁，否则会造成内存泄漏现象。快速排序的部分迭代过程如下图所示：

---

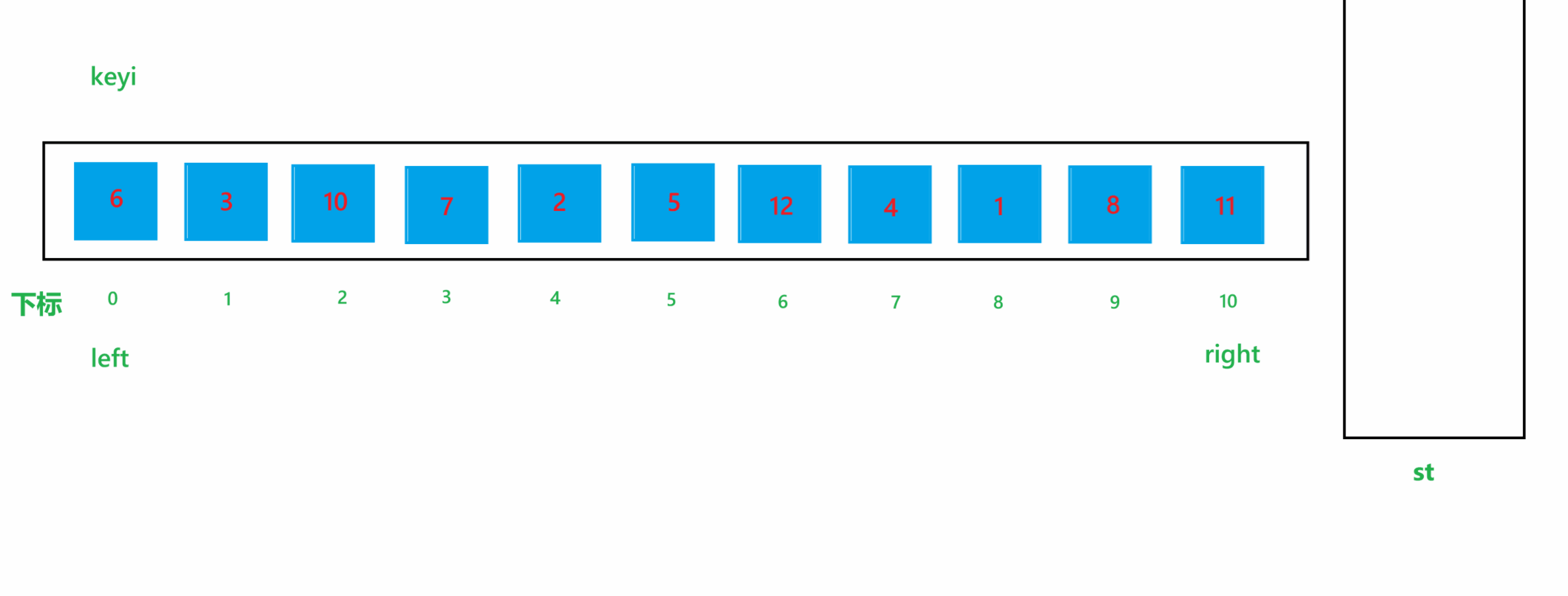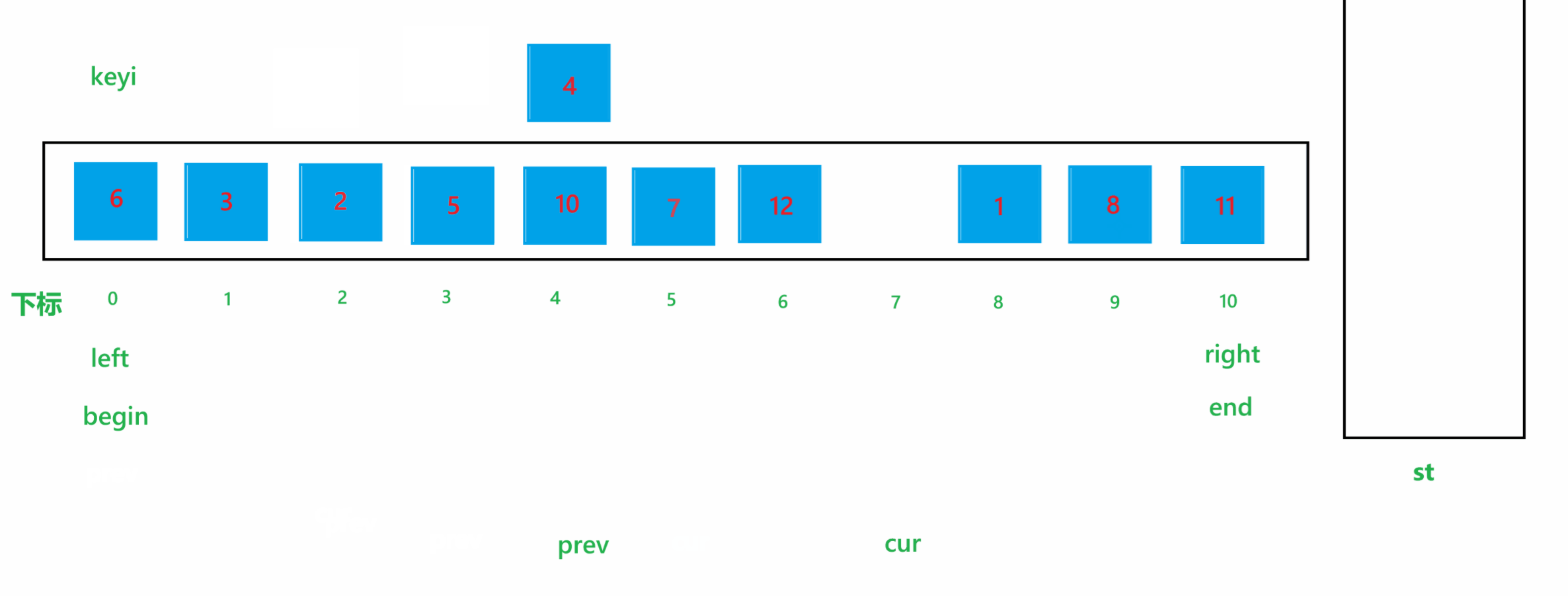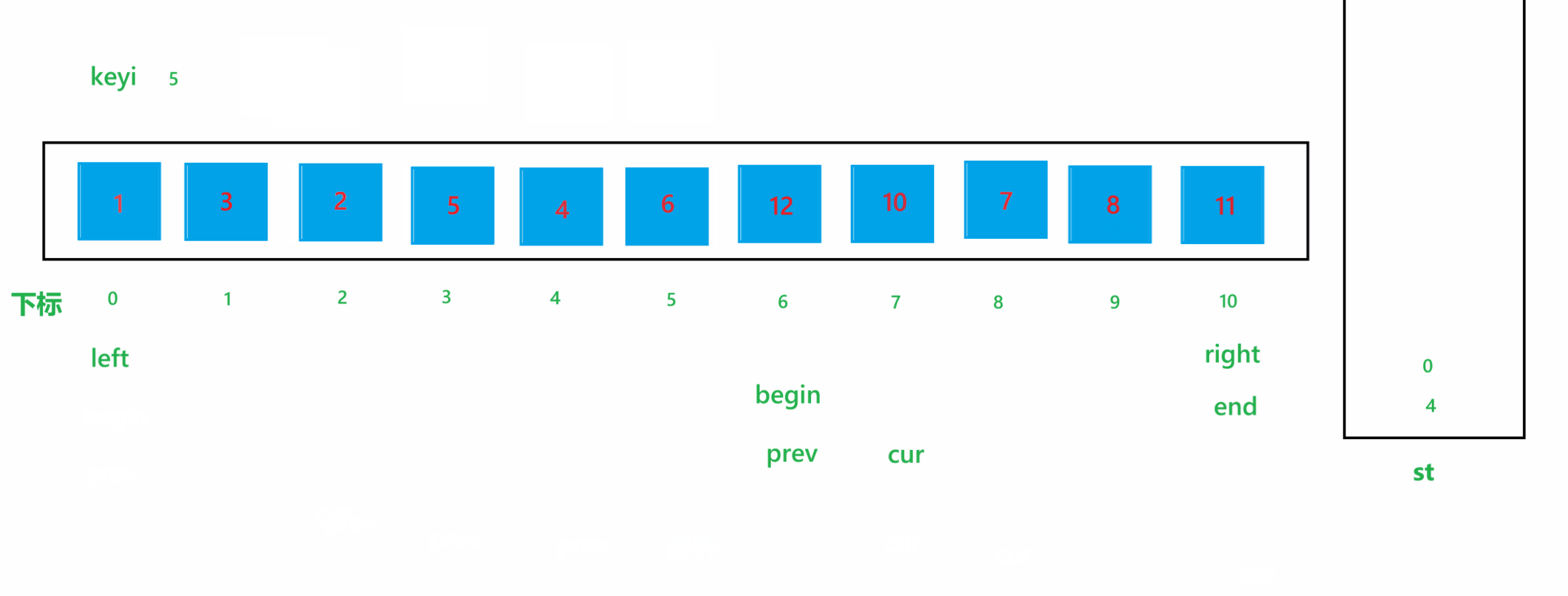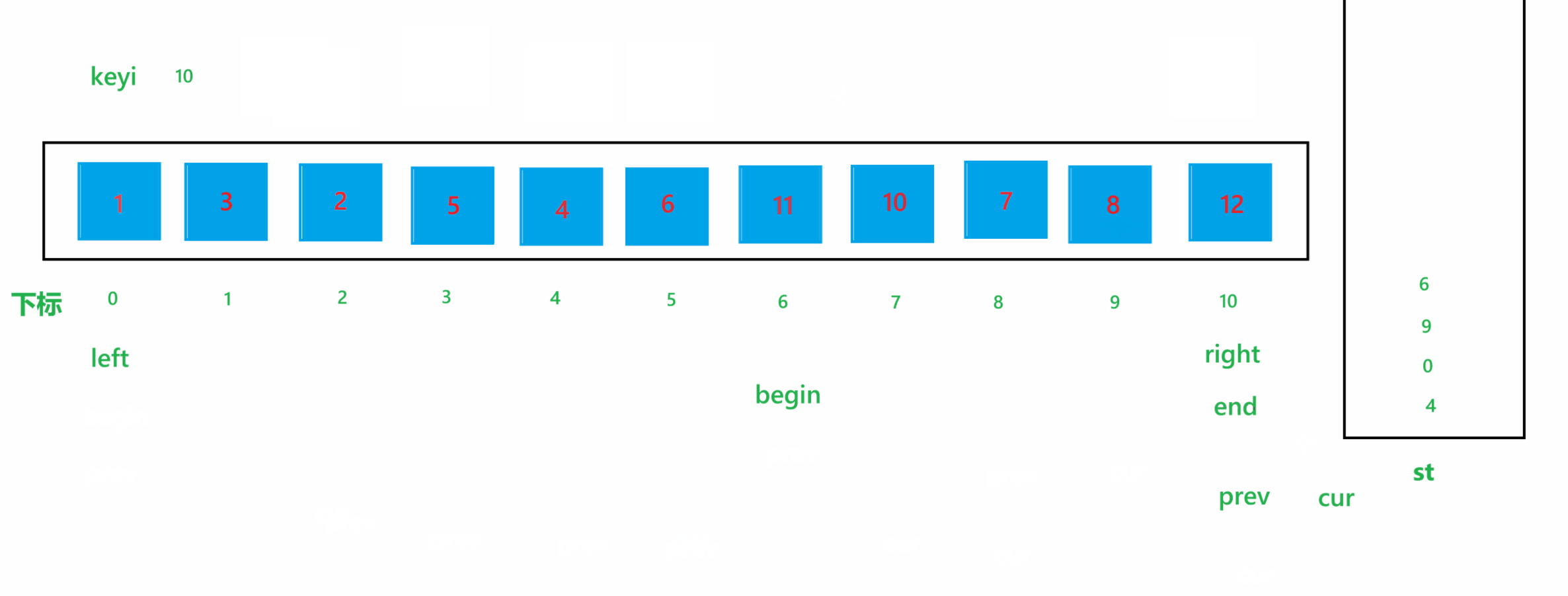
2） 代码

void QuickSortNorR(int* arr, int left, int right)
{//初始化栈Stack st;StackInit(&st);//让左右序号入栈StackPush(&st, right);StackPush(&st, left);//判断栈为不为空while (!StackEmpty(&st)){//取前两个栈顶元素，作为左边和右边的元素int begin = StackTop(&st);StackPop(&st);int end = StackTop(&st);StackPop(&st);//找基准值int keyi = left;int prev = left;int cur = prev + 1;while (cur <= end){if (arr[cur] < arr[keyi] && ++prev != cur)Swap(&arr[prev], &arr[cur]);cur++;}Swap(&arr[prev], &arr[keyi]);keyi = prev;//如果基准值左边的下标大于begin，那就入栈if (keyi - 1 > begin){StackPush(&st, keyi - 1);StackPush(&st, begin);}if (keyi + 1 < end){StackPush(&st, end);StackPush(&st, keyi + 1);}}//销毁栈StackDestroy(&st);
}  

---

3  快速排序的缺陷以及优化

1） 缺陷

  前面我们提到过，快速排序的时间复杂度度是 O(nlogn) 的，但是当数组中的元素为降序或者有大量的重复元素时，其时间复杂度是会退化为 O(n^2) 的。因为如果元素是降序的话，那么就不会在中间位置划分子问题，而是只存在比 key 值小子数组的子问题，不存在比 key 值大子数组的子问题，此时的递归树就由二叉树退化为了单叉树，如：

此时递归树的深度就会变为 n，而不是 logn 了。所以当数组中的元素为降序时，快速排序的时间复杂度就会退化为 O(n^2)。有大量重复元素也类似于是数组中的元素是降序的情况，可以自己试着分析一下。

---

2） 优化

（1） 三路划分

  三路划分主要是应用于优化数组中有大量重复值的情况下导致快速排序性能下降的一种优化方法。三路主要是指将数组中的元素划分为三部分，一部分是比 key 值小的部分，一部分是与 key 值相等的部分，一部分是比 key 值大的部分，由于数组被划分为了三部分，所以叫做三路划分。其算法思想为：

a. 定义某个子问题的数组（这里假设数组为 arr）最左边元素的下标为 left ，最右边元素的下标为 right，最左边的元素值为 key，定义 cur = left + 1，begin = left，end = right

b. 当 arr[cur] < key 时，就交换 arr[cur] 和 arr[left] ，然后 cur++，left++

c. 当 arr[cur] > key 时，就交换 arr[right] 和 arr[cur] ，然后只让 right--

d. 当 arr[cur] == key 时，只让 cur++

e. 当 cur > right 时，结束循环

等循环结束之后，left 和 right 就会指向与 key 值相等的区间，那么再对 [begin, left - 1] 和 [right + 1, end] 继续递归就可以了。这里给大家一个测试用例，执行过程大家可以自己试着画一下：

数组元素： 6 1 7 6 8 6 6 9

代码

void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}int key = arr[left];int begin = left, end = right;int cur = left + 1;while (cur <= right){if (arr[cur] < key)Swap(&arr[cur++], &arr[left++]);else if (arr[cur] > key)Swap(&arr[cur], &arr[right--]);else++cur;}//数组被划分为 [begin, left - 1] [left, right] [right + 1, end]QuickSort(arr, begin, left - 1);QuickSort(arr, right + 1, end);
}

测试用例：

int main()
{int arr[] = { 2, 2, 2, 2, 1, 9, 10, 2, 2, 6, 8, 7 };int n = sizeof(arr) / sizeof(arr[0]);QuickSort(arr, 0, n - 1);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}return 0;
}

---

（2） 内省排序(IntroSort) 

  内省排序，英文全称为 Introspective Sort，是由 David R.Musser 在1997年提出的一中排序算法。内省排序，顾名思义，就是这个排序会自我反省，当递归深度过深，导致性能下降时，该排序算法就会采用别的排序算法来提高性能。该算法的算法思想为：

a. 开始先使用快速排序算法，不过会设计两个变量 logn 和 depth 来记录数组元素个数的 logn 是多少以及当前递归的深度

b. 当子问题的数组元素不大于 16 个元素时，采用直接插入排序

c. 当 depth > 2 * logn 时（这里可以自己设定，1 * logn 或者 3 * logn 都可以），采用堆排序 

代码

void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 1; i < n; i++){int end = i - 1;int tmp = arr[i];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];--end;}else break;}arr[end + 1] = tmp;}
}//向下调整函数
void AdjustDown(int* arr, int n, int parent)
{int child = 2 * parent + 1;if (child + 1 < n && arr[child] < arr[child + 1]){child++;}while (child < n){if (arr[child] > arr[parent]){Swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;}elsebreak;}
}//堆排序
void HeapSort(int* arr, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}int end = n - 1;while (end >= 0){Swap(&arr[0], &arr[end--]);AdjustDown(arr, end + 1, 0);}
}//内省排序
void IntroSort(int* arr, int left, int right, int depth, int defaultdepth)
{if (left >= right) return;//数组元素不超过16个时，采用直接插入排序if (right - left + 1 <= 16){InsertSort(arr + left, right - left + 1);return;}//如果递归深度超过标准，采用堆排序if (depth > defaultdepth){HeapSort(arr + left, right - left + 1);return;}//采用快速排序++depth;//递归深度需要 +1int prev = left, cur = left + 1;while (cur <= right){if (arr[cur] < arr[left] && ++prev != cur) Swap(&arr[cur], &arr[prev]);++cur;}Swap(&arr[left], &arr[prev]);//[left, prev - 1] prev [prev + 1, right]IntroSort(arr, left, prev - 1, depth, defaultdepth);IntroSort(arr, prev + 1, right, depth, defaultdepth);
}//快排主函数
void QuickSort(int* arr, int left, int right)
{int depth = 0;//记录当前递归的深度int logn = 0;//记录数组元素个数的 logn 是多少int N = right - left + 1;for (int i = 1; i < N; i *= 2){logn++;}IntroSort(arr, left, right, depth, 2 * logn);
}

测试用例：

int main()
{int arr[100] = { 0 };//采用随机数，更加具有普遍性srand(time(NULL));int n = sizeof(arr) / sizeof(arr[0]);for (int i = 0; i < n; i++){arr[i] = rand() % (i + 1);}QuickSort(arr, 0, n - 1);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}return 0;
}

---

4  总结

  快速排序是特别重要的一个排序算法，因为其排序性能特别好，所以在许多语言官方的排序函数底层都是使用的快速排序的算法思想，比如：C++ 中 STL （后面C++ 会讲解）里面的sort函数，使用的就是内省排序算法思想。所以，大家一定要把快速排序学好，对于后面学习非常有帮助。