数据结构——二叉树,堆
目录
1.树
1.1树的概念
1.2树的结构
2.二叉树
2.1二叉树的概念
2.2特殊的二叉树
2.3二叉树的性质
2.4二叉树的存储结构
2.4.1顺序结构
2.4.2链式结构
3.堆
3.1堆的概念
3.2堆的分类
3.3堆的实现
3.3.1初始化
3.3.2堆的构建
3.3.3堆的销毁
3.3.4堆的插入
3.3.5堆的删除
3.3.6取堆顶的数据
3.3.7堆的数据个数
3.3.8堆的判空
3.4堆排序
3.5 TOP-K问题
4.二叉树链式结构的实现
4.1二叉树结构
4.2二叉树遍历
4.2.1前序遍历
4.2.2中序遍历
4.2.3后序遍历
4.2.4层序遍历
4.3基础接口实现
4.3.1二叉树结点个数
4.3.2二叉树的高度
4.3.3 二叉树叶子结点个数
4.3.4 二叉树第k层结点个数
4.3.5 二叉树查找值为x的结点
4.3.6 通过前序遍历的数组构建二叉树
4.3.7 二叉树销毁
4.3.8 判断二叉树是否是完全二叉树
1.树
1.1树的概念

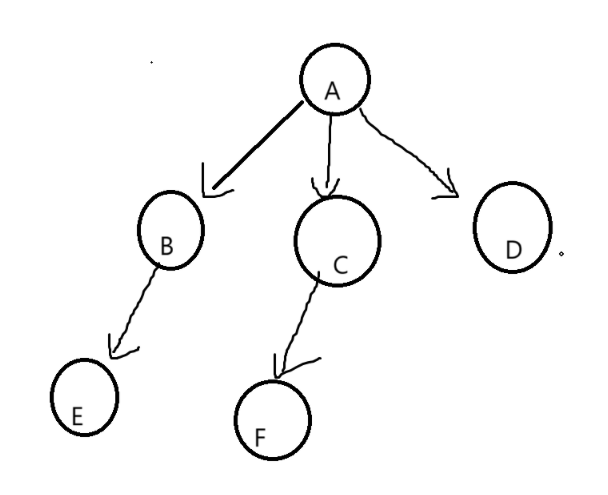
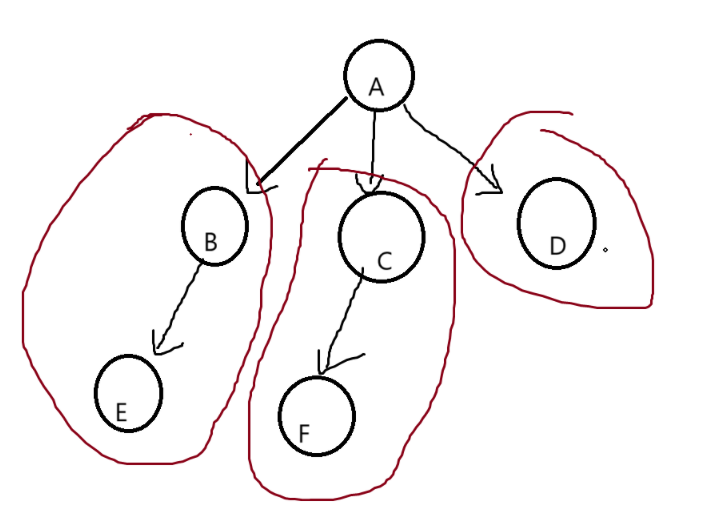
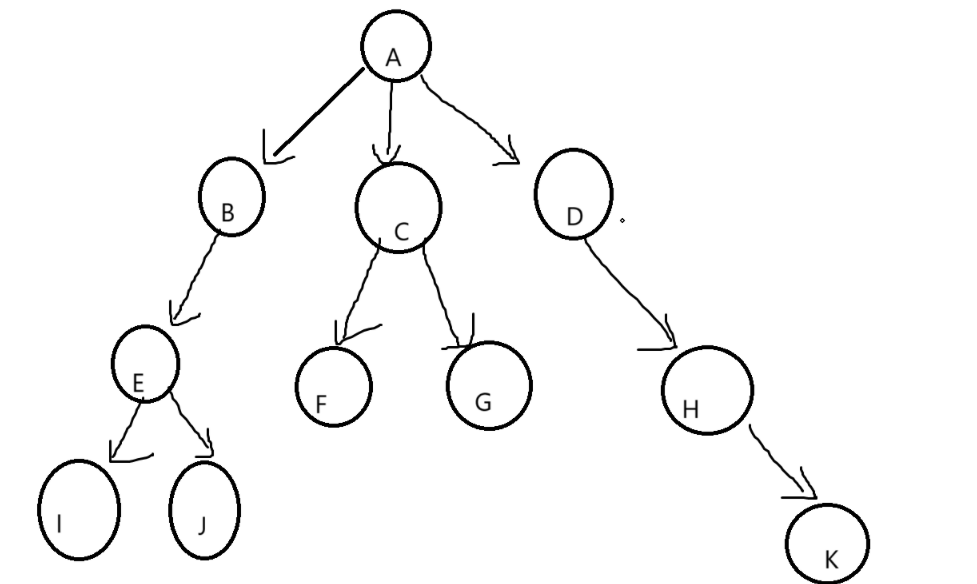
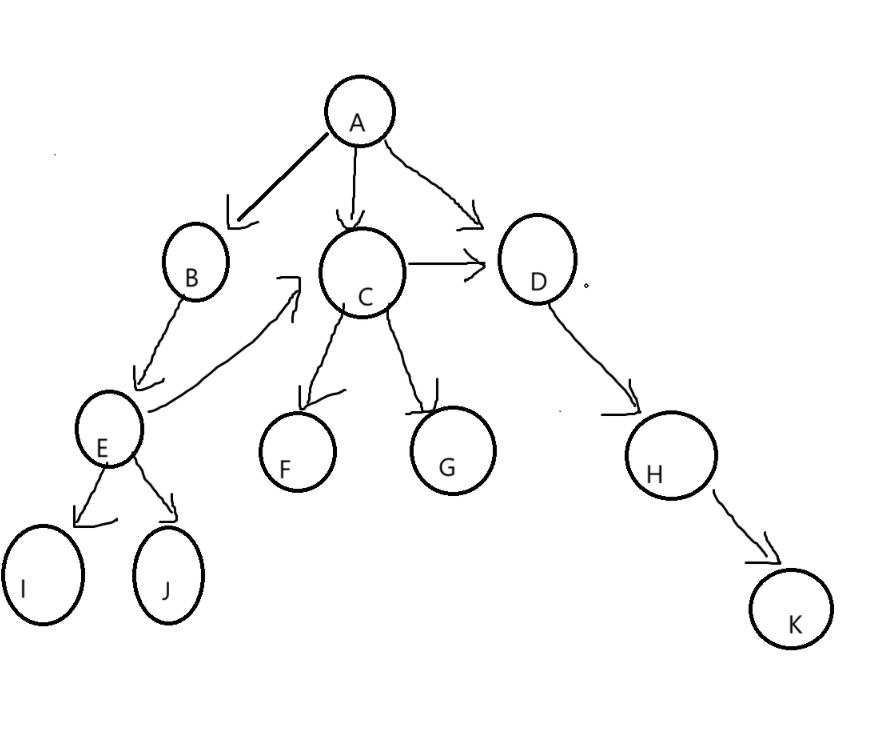
1.2树的结构
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点struct Node* pNextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
};2.二叉树
2.1二叉树的概念
树的度为2的树,可以为空,也可以只有一个(根)节点,只有左右子树和节点
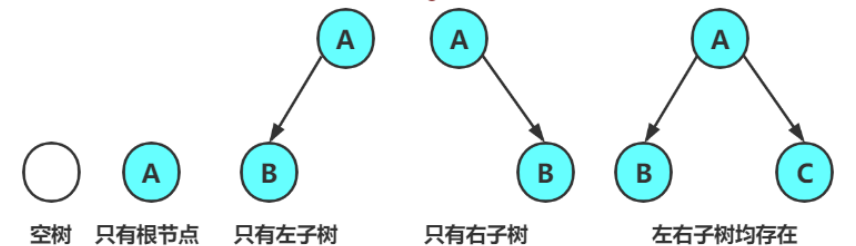
2.2特殊的二叉树
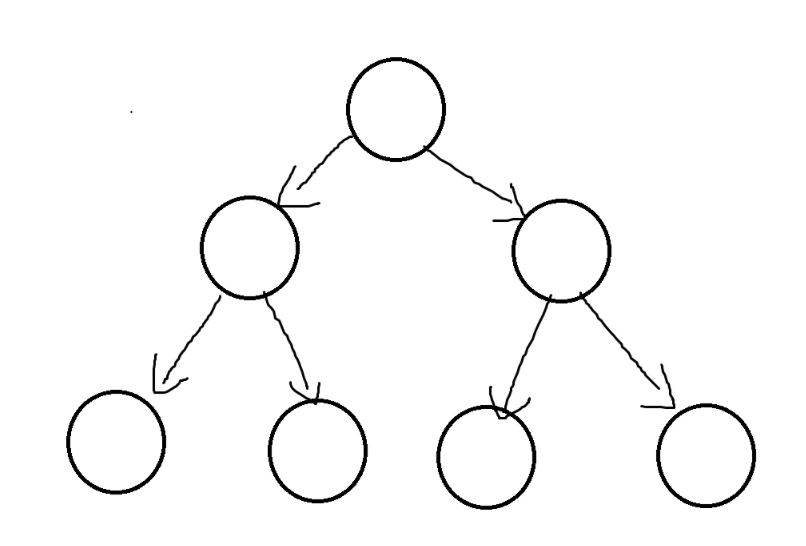
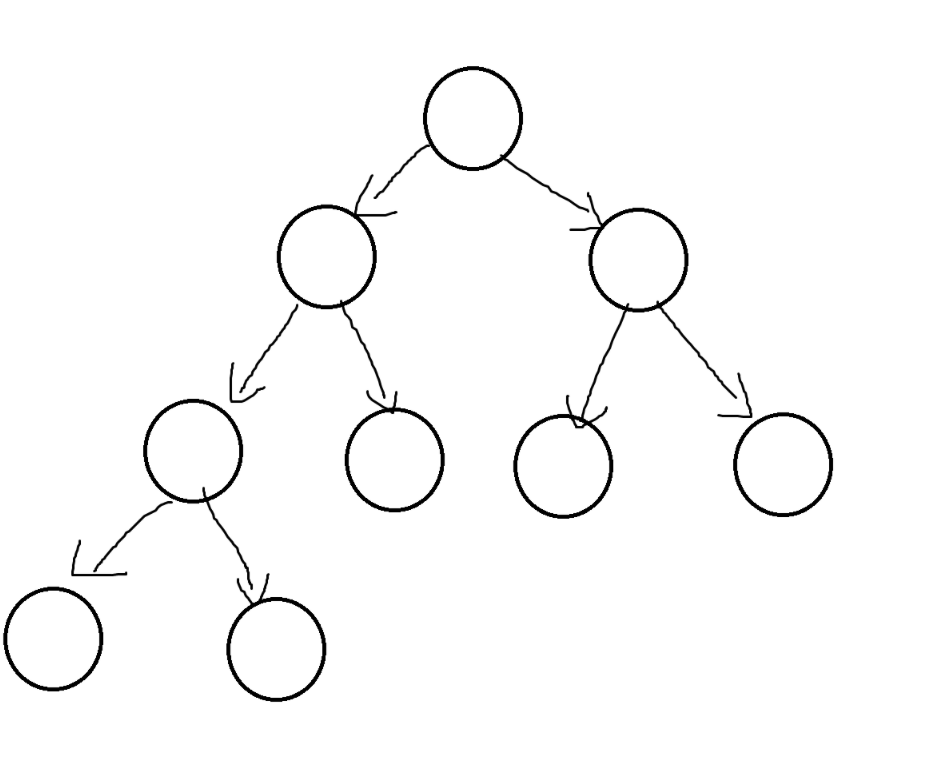
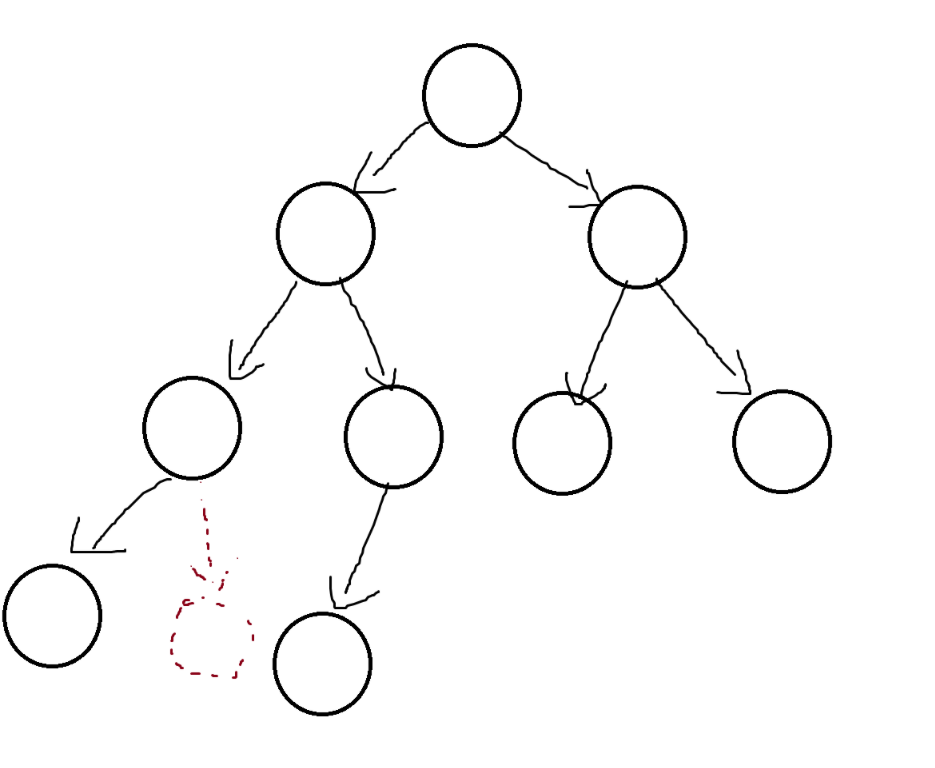
2.3二叉树的性质
1. 若规定根结点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有 2 *(i-1)个结点(*代表次方)2. 若规定根结点的层数为 1 ,则 深度为 h的二叉树的最大结点数是 2*h-1(*代表次方)3. 对任何一棵二叉树 , 如果度为 0 其叶结点个数为 , 度为 2 的分支结点个数为 , 则有 = + 14. 若规定根结点的层数为 1 ,具有 n 个结点的满二叉树的深度 , h=log(n+1)(ps :是log 以 2为底,n+1 为对数 )5. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从 0 开始编号,则对于序号为i 的结点有:1. 若 i>0 , i 位置结点的双亲序号: (i-1)/2 ; i=0 , i 为根结点编号,无双亲结点2. 若 2i+1<n ,左孩子序号: 2i+1 , 2i+1>=n 否则无左孩子3. 若 2i+2<n ,右孩子序号: 2i+2 , 2i+2>=n 否则无右孩子
2.4二叉树的存储结构
2.4.1顺序结构
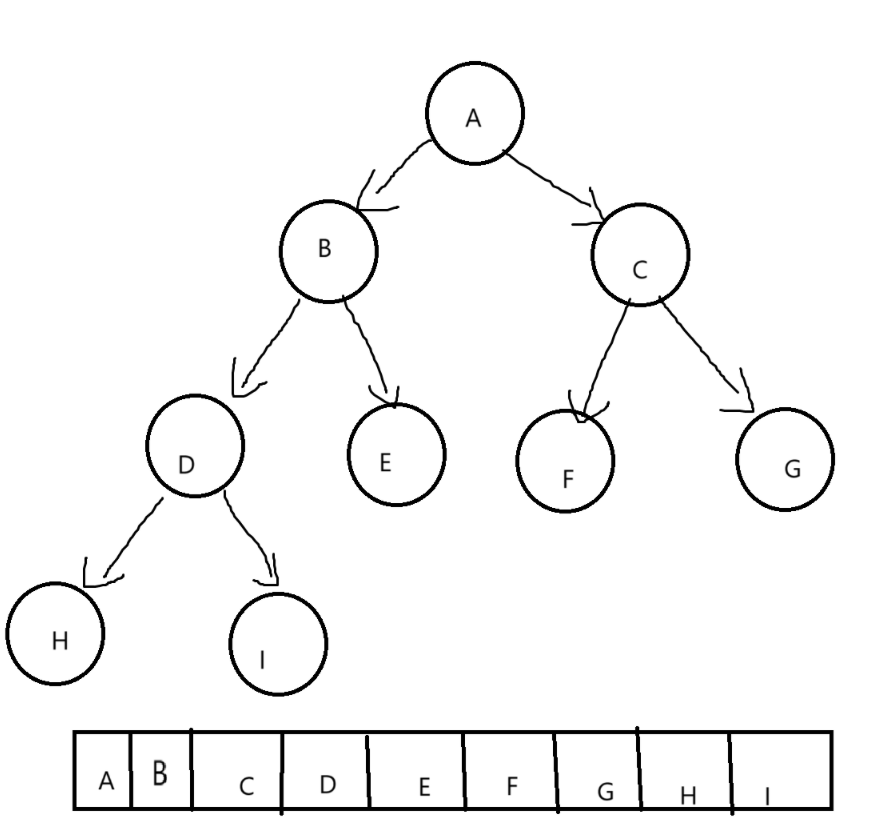
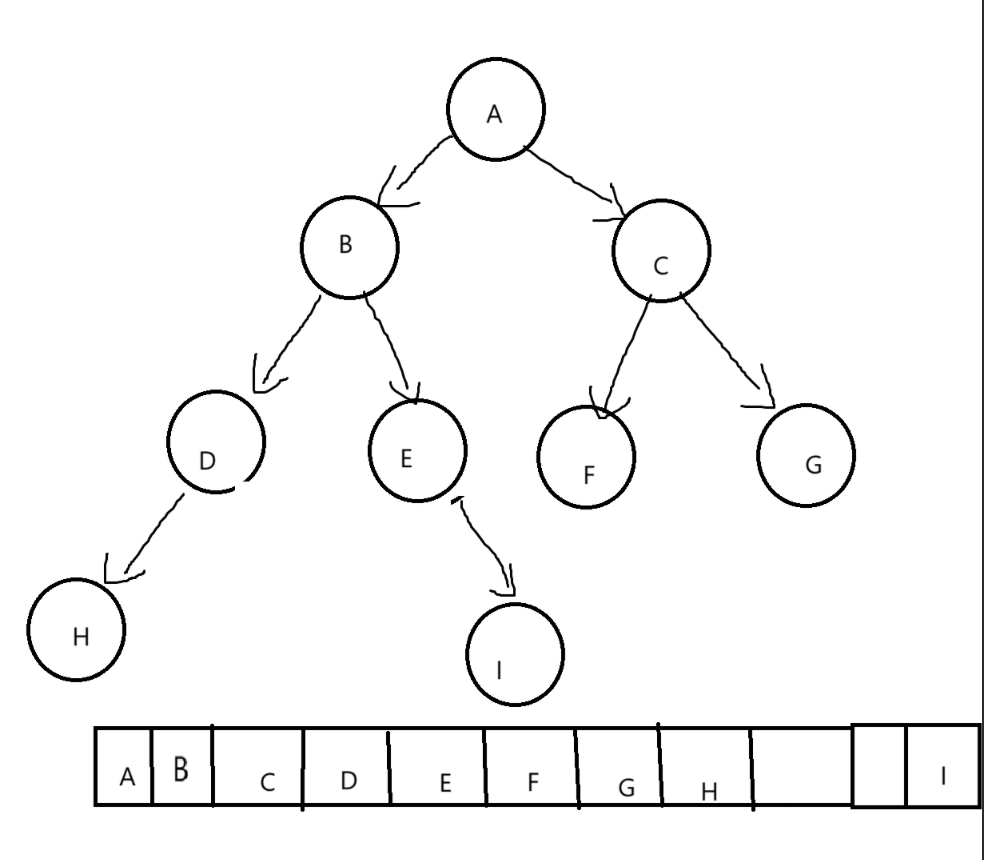
2.4.2链式结构
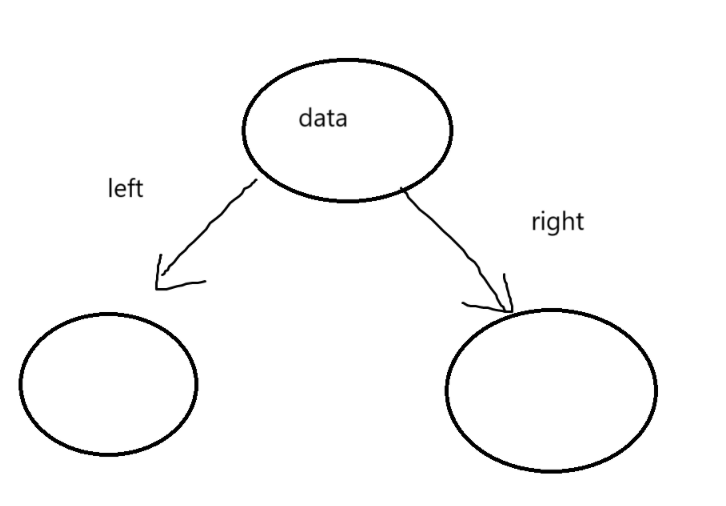
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* left; // 指向当前结点左孩子struct BinTreeNode* right; // 指向当前结点右孩子BTDataType data; // 当前结点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* parent; // 指向当前结点的双亲struct BinTreeNode* left; // 指向当前结点左孩子struct BinTreeNode* right; // 指向当前结点右孩子int data; // 当前结点值域
};3.堆
3.1堆的概念
就是一种二叉树,储存的方式是数组
3.2堆的分类
完全二叉树用数组存储堆有两种类型一种是小跟堆,一种是大根堆
小跟堆:任何一个父节点<=子节点
逻辑

存储

大根堆:任何一个父节点>=子节点
逻辑

存储

3.3堆的实现
创建文件不再叙述
3.3.1初始化
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;3.3.2堆的构建
void HeapCreate(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}3.3.3堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}3.3.4堆的插入
当插入一个数据时,此时可能不符合小堆(大堆),因此插入一个数据化,要对数据进行调整,此时我们就要用到向上调整算法
用小堆举例
当我们数据插入到最后一位时,根据小堆性质(任何一个父节点<=子节点)与当前节点的父节点比较,如果父节点>子节点,交换数据,如此重复,直到父节点<=子节点,或者子节点在数组的位置<=0跳出;
//向上调整
void AdjustUp(HPDataType* HP, int child)
{int parent = (child - 1) / 2;//找到父节点while (child > 0){if (HP[parent] > HP[child])//建小堆,父节点<=子节点{swap(&HP[parent], &HP[child]);child = parent;parent = (child - 1) / 2;}//if (HP[parent] < HP[child])//建大堆,父节点>=子节点//{// swap(&HP[parent], &HP[child]);// child = parent;// parent = (child - 1) / 2;//}else{break;}}
}
//交换数据
void swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//扩容if (hp->_capacity == hp->_size){int tmp = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;HPDataType* new = (HPDataType*)ralloc(hp->_a, 2 * sizeof(HPDataType));if (new == NULL){perror("new");return;}hp->_capacity = tmp;hp->_a = new;}hp->_a[hp->_size++] = x;向上调整AdjustUp(hp->_a, hp->_size - 1);//第一个参数的数组指针,第二个参数是x在数组的位置
}3.3.5堆的删除
对于堆的删除,我们不是删除堆的最后一个元素,而是删除堆顶的数据,也就是根节点的数据,对于根节点数据的删除,我们不能直接把数组的一个数据覆盖(根节点的数据)


我们发现直接覆盖根节点,父子关系就会混乱,同时小堆(大堆)的特性也会消失
这里,我们就可以用到,向下调整算法
同样用小堆举例
当删除数据之前,先把堆顶元素与最后一个元素交换,之后删除最后一个元素,对堆顶数据进行向下调整,当数据交换后,根据小堆性质(任何一个父节点<=子节点),先判断左右子节点那个小,与较小的子节点比较,如果父节点>子节点,交换数据,如此重复,直到父节点数据<=子节点数据,或者子节点在数组的位置>=n(数组内有效数组个数后一位)跳出;

void AdjustDown(HPDataType* HP, int n,int parent)
{//假设左孩子小int child = parent * 2 + 1;while (child < n){if (child+1<n && HP[child] > HP[child + 1]){child++;}if (HP[child] < HP[parent]){swap(&HP[child], &HP[parent]);parent = child;child = parent * 2 + 1;}//假设左孩子大//if (child + 1 < n && HP[child] > HP[child + 1])//大堆//{// child++;//}//if (HP[child] > HP[parent])//{// swap(&HP[child], &HP[parent]);// parent = child;// child = parent * 2 + 1;//}else{break;}}
}
void HeapPop(Heap* hp)
{assert(hp);assert(hp->_size > 0);Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;AdjustDown(hp->_a, hp->_size, 0);
}其实这里有点有排序的意味,当我们每次pop都是堆里最小的元素,当pop完整个数组,对于小堆,就可以获取一份从小到大的数据,但是这里并不是排序,这里我们只是打印排序,并没有把数组中的元素排序
3.3.6取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(hp->_size > 0);return hp->_a[0];
}3.3.7堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}3.3.8堆的判空
// 堆的判空
int HeapEmpty(Heap* hp)
{return hp->_size == 0;
}3.4堆排序
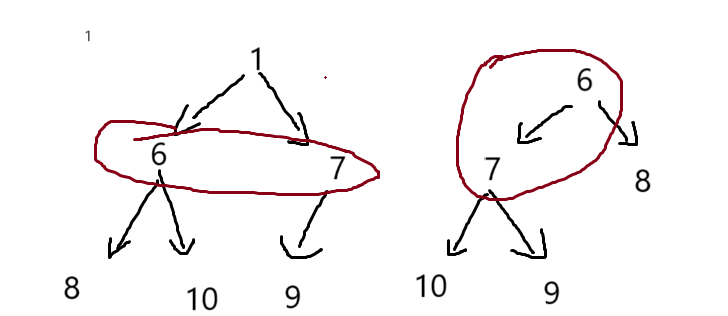
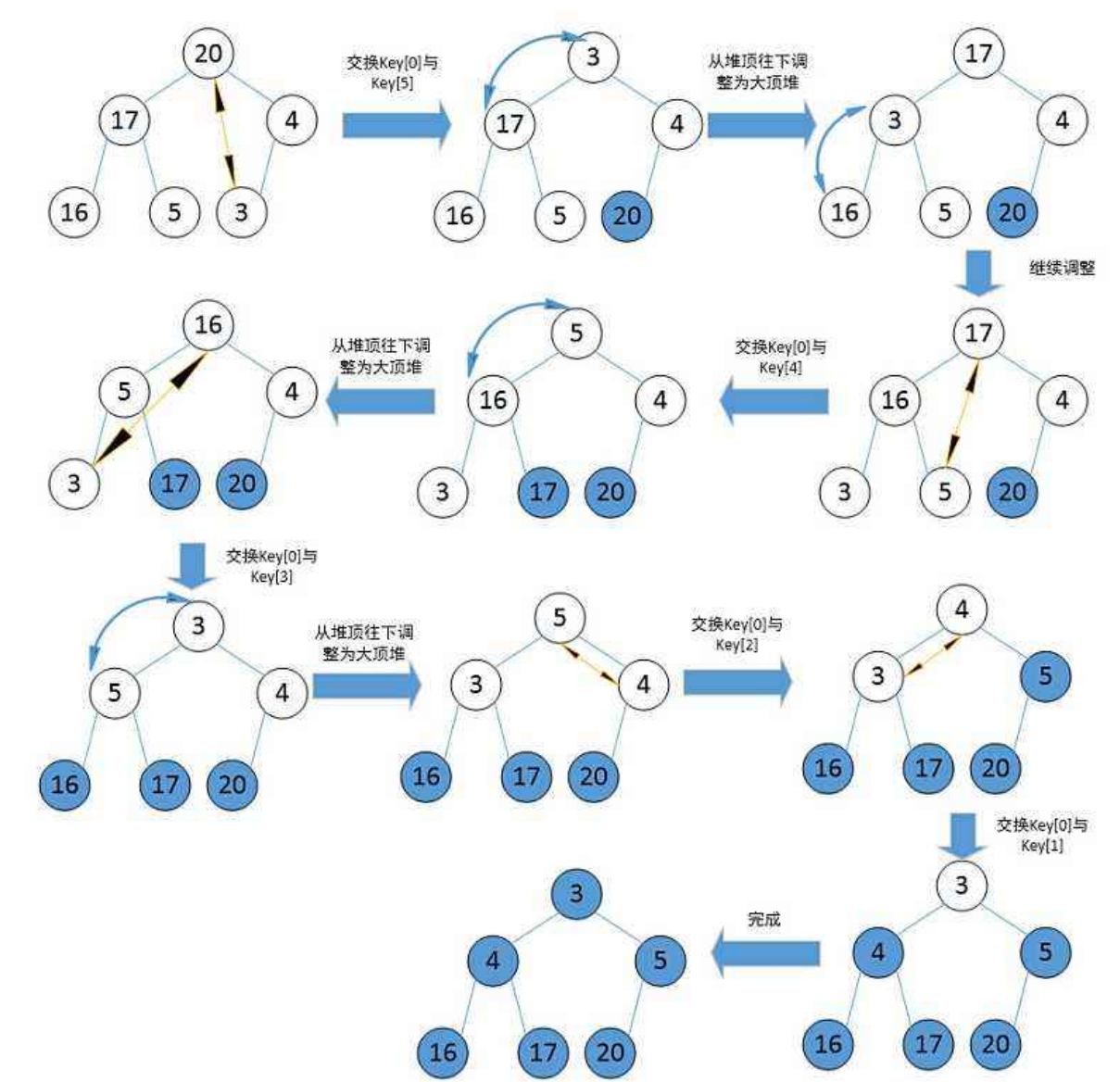
void HeapSort()
{int a[] = { 4,8,1,5,6,9,7,3,2};Heap hp;//升序建大堆//降序建小堆int n = sizeof(a) / sizeof(int);for (int i = 0; i <n; i++){AdjustUp(a, i);}int end = n-1;//最后一个元素的位置while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}![]()
对于向上调整建堆,它的时间复杂度是O(N*logN)
当我们用向下调整算法建堆时,时间复杂度为O(N)(此文章不做证明,有兴趣可以去查询)
void HeapSort()
{int a[] = { 4,8,1,5,6,9,7,3,2};Heap hp;//升序建大堆//降序建小堆int n = sizeof(a) / sizeof(int);int end = n-1;//最后一个元素的位置for (int i = (end - 1) / 2; i >= 0; i--)//(end - 1) / 2求父亲节点{AdjustDown(a, i, 0);}while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}3.5 TOP-K问题
前 k 个最大的元素,则建小堆前 k 个最小的元素,则建大堆
//创建数据
void CreateNDate()
{// 造数据int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}
void TestHeap()
{int k;printf("请输入k>:");scanf("%d", &k);int* kminheap = (int*)malloc(sizeof(int) * k);if (kminheap == NULL){perror("malloc fail");return;}const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;}// 读取文件中前k个数for (int i = 0; i < k; i++){fscanf(fout, "%d", &kminheap[i]);}// 建K个数的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminheap, k, i);}// 读取剩下的N-K个数int x = 0;while (fscanf(fout, "%d", &x) > 0)//读取文件剩下的数据{if (x > kminheap[0]){kminheap[0] = x;AdjustDown(kminheap, k, 0);}}printf("最大前%d个数:", k);for (int i = 0; i < k; i++){printf("%d ", kminheap[i]);}printf("\n");
}int main()
{//创建数据CreateNDate();TestHeap();return 0;
}如何确定这前k个数是最大的,在创建数据时可以模上一个数,int x = (rand() + i) % 10000000;
就像这样,代表随机出来的数不可能超过10000000,之后我们可以在文件中改变几个数据,让这几个数据大于10000000,然后运行程序,看看前k个数是否为你改的几个数。
4.二叉树链式结构的实现
4.1二叉树结构
1. 空树2. 非空:根结点,根结点的左子树、根结点的右子树组成的。
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}
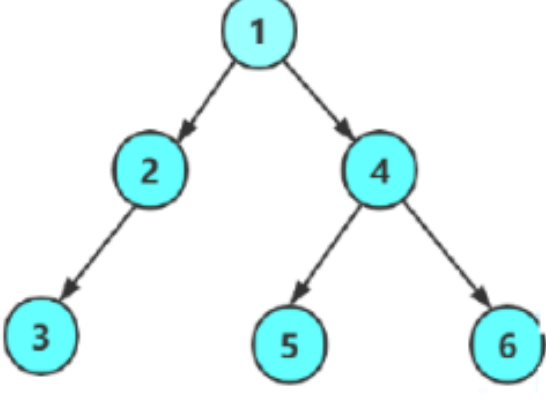
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}
4.2二叉树遍历
1. 前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。2. 中序遍历 (Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中(间)。3. 后序遍历 (Postorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之后。
4.2.1前序遍历
根 左子树 右子树


void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->_data);PrevOrder(root->_left);PrevOrder(root->_right);
}4.2.2中序遍历
左子树 根 右子树

void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->_left);printf("%d ", root->_data);InOrder(root->_right);
}4.2.3后序遍历
左子树 右子树 根

void Postorde(BTNode* root)
{if (root == NULL){printf("N ");return;}Postorde(root->_left);Postorde(root->_right);printf("%d ", root->_data);
}4.2.4层序遍历
每层每层遍历


遍历的结果就是1,2,3,4,5,6,而这种遍历则需要用到队列来实现,当把1放进队列,把1的左右节点放进队列,把1丢出,再把2和4的左右节点放进队列,把2,4丢出,重复如此,就完成了层序遍历
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//初始化队列if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->_data);if (front->_left){QueuePush(&q,front->_left);}if (front->_right){QueuePush(&q, front->_right);}}QueueDestroy(&q);//队列销毁
}4.3基础接口实现
4.3.1二叉树结点个数
int size = 0;
int TreeSize(BTNode* root)
{if (root == NULL)return 0;else++size;TreeSize(root->_left);TreeSize(root->_right);return size;
}对于这个程序,每次我们调用都要使size=0,我们可以优化一下
int TreeSize(BTNode* root)
{return root == NULL ? 0 :TreeSize(root->_left) + TreeSize(root->_right) + 1;
}这个就相当于左子树的节点+右子树的节点+1(自己本身)
4.3.2二叉树的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return TreeHeight(root->left) > TreeHeight(root->right) ?TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}这个程序有一些效率问题,每次判断完后,还要进入递归,导致重复计算很多,效率很低,因此可以用一个变量来存储
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->_left);int rightHeight = TreeHeight(root->_right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}4.3.3 二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL)//判断是否是叶子节点{return 1;}return BinaryTreeLeafSize(root->_left)+BinaryTreeLeafSize(root->_right);//递归左右子树}4.3.4 二叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)//根节点为第一层
{if (k == 1){return 1;}if (root == NULL){return 0;}return BinaryTreeLevelKSize(root->_left, k - 1) +BinaryTreeLevelKSize(root->_right, k - 1);//递归左右子树
}4.3.5 二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root->_data == x){return root;}BTNode* ret = BinaryTreeFind(root->_left, x);//存储结果if (ret)//当查到就返回{return ret;}return BinaryTreeFind(root->_right, x);
}4.3.6 通过前序遍历的数组构建二叉树
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(char* a, int n, int* pi)//char*a代表要构建的数据 n代表a内的数据个数
{if (a[*pi] == '#'){(*pi)++;return NULL;}if (n == *pi){return NULL;}BTNode* ret = (BTNode*)malloc(sizeof(BTNode));ret->_data = a[(*pi)++];ret->_left = BinaryTreeCreate(a,n,pi);ret->_right = BinaryTreeCreate(a,n,pi);return ret;
}4.3.7 二叉树销毁
对于二叉树的销毁,要选择后序遍历,如果选择前中序遍历销毁,就无法找到所有节点
void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;TreeDestory(root->_left);TreeDestory(root->_right);free(root);
}4.3.8 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}if (front->_left){QueuePush(&q, front->_left);}if (front->_right){QueuePush(&q, front->_right);}}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 如果有非空,就不是完全二叉树if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}相关文章:

数据结构——二叉树,堆
目录 1.树 1.1树的概念 1.2树的结构 2.二叉树 2.1二叉树的概念 2.2特殊的二叉树 2.3二叉树的性质 2.4二叉树的存储结构 2.4.1顺序结构 2.4.2链式结构 3.堆 3.1堆的概念 3.2堆的分类 3.3堆的实现 3.3.1初始化 3.3.2堆的构建 3.3.3堆的销毁 3.3.4堆的插入 3.3.5…...

PostgreSQL 分区表——范围分区SQL实践
PostgreSQL 分区表——范围分区SQL实践 1、环境准备1-1、新增原始表1-2、执行脚本新增2400w行1-3、创建pg分区表-分区键为创建时间1-4、创建24年所有分区1-5、设置默认分区(兜底用)1-6、迁移数据1-7、创建分区表索引 2、SQL增删改查测试2-1、查询速度对比…...

第八节:进阶特性高频题-Pinia与Vuex对比
优势:无嵌套模块、Composition API友好、TypeScript原生支持 核心概念:state、getters、actions(移除mutation) 深度对比 Pinia 与 Vuex:新一代状态管理方案的核心差异 一、核心架构设计对比 维度VuexPinia设计目标集…...

路由交换网络专题 | 第七章 | BGP练习 | 次优路径 | Route-Policy | BGP认证
基本部分配置讲解: 配置BGP相关部分: // BGP区域配置: 用作环回口创建BGP对等体// “ipv4-family unicast”是指进入BGP的IPv4单播地址族视图。 // 配置完后仅仅只在IPV4地址簇下建立对等体。* [AR3]bgp 100 [AR3-bgp]peer 1.1.1.1 as-number 100 [AR…...

序论文42 | patch+MLP用于长序列预测
论文标题:Unlocking the Power of Patch: Patch-Based MLP for Long-Term Time Series Forecasting 论文链接:https://arxiv.org/abs/2405.13575v3 代码链接:https://github.com/TangPeiwang/PatchMLP (后台回复“交流”加入讨…...

【mongodb】系统保留的数据库名
目录 1. admin2. config3. local4. test(非严格保留,但常作为默认测试数据库)5. 注意事项6. 其他相关说明 1. admin 1.用途:用于存储数据库的权限和用户管理相关数据。2.特点:该数据库是 MongoDB 的超级用户数据库&am…...

js 的call 和apply方法用处
主要用于ECMAScript与宿主环境(文档对象(DOM)、浏览器对象(BOM))的交互中; 例子:function changeStyle(attr, value){ this.style[attr] value; } …...

济南国网数字化培训班学习笔记-第二组-2节-输电线路施工及质量
输电线路施工及质量 质量管控基本规定 基本规定 项目分类 土石方(测量挖坑)、基础、杆塔、架线、接地、线路防护 检验项目分类原则: 1.主控项目:影响工程性能、强度、安全性和可靠性,且不易修复和处理 2.一般项…...
从 daz3d 导入到 UE5。在 UE5 中,我发现使用某个表情并与闭眼混合后,上眼睑出现了问题)
“Daz to Unreal”将 G8 角色(包括表情)从 daz3d 导入到 UE5。在 UE5 中,我发现使用某个表情并与闭眼混合后,上眼睑出现了问题
1) Bake & Export Corrective Morphs from Daz before you go into UE5 1) 在进入 UE5 之前,从 Daz 烘焙并导出修正型变形 In Daz Studio 在 Daz Studio 中 Load your G8 head, dial in the exact mix (e.g. Smile 1.0 Eyes Closed 1.0). 加载你的 G8 头部&am…...

Linux系统之----进程优先级、调度与切换
在开启本篇文章的学习之前,我们先要熟悉如下两个事 1.概念 进程优先级指的是进程能得到某种资源的先后顺序,要理解好它与权限的关系,优先级是 能,拥有资源的先后顺序,权限是 能还是不能的问题 2.为什么要有优先级…...

Web3钱包开发功能部署设计
Web3钱包开发功能部署设计全景指南(2025技术架构与实战) ——从核心模块到多链生态的完整解决方案 一、核心功能模块设计 1.1 资产管理体系 Web3钱包的核心功能围绕资产存储、交易验证、多链兼容展开: • 密钥管理:…...

【含文档+PPT+源码】基于SpringBoot的开放实验管理平台设计与实现
项目介绍 本课程演示的是一款基于SpringBoot的开放实验管理平台设计与实现,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的 Java 学习者。 1.包含:项目源码、项目文档、数据库脚本、软件工具等所有资料 2.带你从零开始部署运行本套系统…...

小刚说C语言刷题——1317正多边形每个内角的度数?
1.题目描述 根据多边形内角和定理,正多边形内角和等于:( n-2 ) 180∘ ( n 大于等于 3且 n 为整数) 请根据正多边形的边数,计算该正多边形每个内角的度数。(结果保留1位小数&#x…...

Spring—AOP
AOP是在不惊动原有的代码的基础上对功能进行增强操作 连接点:JoinPoint,可以被AOP控制的方法 通知:Advice,增强的逻辑,共性功能 切入点:PointCut,匹配连接点的条件,表明连接点中哪…...

算法训练营第二天| 209.长度最小的子数组、59.螺旋矩阵II、区间和
209.长度最小的子数组 题目 思路与解法 **第一想法:**无 carl的讲解: 滑动窗口 class Solution:def minSubArrayLen(self, target: int, nums: List[int]) -> int:ij0lens len(nums)sum 0res lens 1while j < lens:# for m in range(i, j1)…...

【C++ 真题】P3456 [POI2007] GRZ-Ridges and Valleys
[POI2007] GRZ-Ridges and Valleys 题面翻译 题目描述 译自 POI 2007 Stage 2. Day 0「Ridges and Valleys」 给定一个 n n n \times n nn 的网格状地图,每个方格 ( i , j ) (i,j) (i,j) 有一个高度 w i j w_{ij} wij。如果两个方格有公共顶点,…...

Vue3 中 computed的详细用法
Vue 3 中 computed 是一个非常重要的响应式 API,它是基于其依赖项的值来计算得出的值,当依赖项发生变化时,计算属性会自动更新 基本用法 在选项式 API 中,computed 通常作为一个选项直接在组件的选项对象中定义。例如 <temp…...

位带和位带别名区
位带区域和位带别名区域 位带区域(Bit-banding)是一种技术, 允许开发者直接访问和修改内存中的单个位。 这种技术在某些微控制器(如ARM Cortex-M系列)中特别有用,因为它可以简化对寄存器位的访问和修改。 …...

DRF凭什么更高效?Django原生API与DRF框架开发对比解析
一、原生 Django 开发 API 的局限性 虽然 Django 可以通过 JsonResponse 和视图函数手动构建 API,但存在以下问题: 手动序列化与反序列化 需要手动将模型实例转换为 JSON,处理复杂数据类型(如嵌套关系)时代码冗长且易…...

Agent智能体应用详解:从理论到实践的技术探索
一、Agent智能体是什么? 1. 核心定义 Agent智能体是能够感知环境、自主决策并执行动作以实现目标的软件实体。其核心特征包括: 自主性:无需外部指令持续运行。 反应性:实时响应环境变化。 目标导向:基于预设或学习…...

Windows下使用 VS Code + g++ 开发 Qt GUI 项目的完整指南
🚀 使用 VS Code g 开发 Qt GUI 项目的完整指南(Windows MSYS2) 本指南帮助你在 Windows 下使用 VS Code g CMake Qt6 快速搭建 Qt GUI 项目,适合熟悉 Visual Studio 的开发者向跨平台 VS Code 工具链迁移。 🛠️…...

arm64适配系列文章-第三章-arm64环境上mariadb的部署
ARM64适配系列文章 第一章 arm64环境上kubesphere和k8s的部署 第二章 arm64环境上nfs-subdir-external-provisioner的部署 第三章 arm64环境上mariadb的部署 第四章 arm64环境上nacos的部署 第五章 arm64环境上redis的部署 第六章 arm64环境上rabbitmq-management的部署 第七章…...

YOLOv8融合CPA-Enhancer【提高恶略天气的退化图像检测】
1.CPA介绍 CPA-Enhancer通过链式思考提示机制实现了对未知退化条件下图像的自适应增强,显著提升了物体检测性能。其插件式设计便于集成到现有检测框架中,并在物体检测及其他视觉任务中设立了新的性能标准,展现了广泛的应用潜力。 关于CPA-E…...
)
编译 C++ 报错“找不到 g++ 编译器”的终极解决方案(含 Windows/Linux/macOS)
前言 在使用终端编译 C 程序时,报错: 或类似提示,意味着你的系统尚未正确安装或配置 g 编译器。本篇将从零手把手教你在 Windows / Linux / macOS 下安装并配置 g,适用于新手或 C 入门阶段的你。 什么是 g? g 是 GN…...

Spring 过滤器详解:从基础到实战应用
Spring 过滤器详解:从基础到实战应用 引言 在 Spring 框架中,过滤器(Filter)是处理 HTTP 请求和响应的重要组件。它们为开发者提供了一种在请求到达控制器之前或响应返回客户端之前进行操作的机制。本文将深入探讨 Spring 中常见…...

达梦并行收集统计信息
达梦收集统计信息速度如何? 答:1分钟1G 大库收集起来可能比较慢,想并行收集需要一些条件 3个参数先了解一下 我把max_parallel_degree改为16 相关说明可以看一下 对一个3G的表收集 收集方法 DBMS_STATS.GATHER_TABLE_STATS( TEST,T1,…...

AOSP CachedAppOptimizer 冻结方案
背景 Android 一直面临一个核心难题:如何优化进程对有限系统资源(如 CPU、电量)的使用,同时保证用户体验。 当进程进入后台后,它们虽不再贡献用户体验,却仍可能消耗资源。传统的杀后台方案虽然节省资源&a…...

JVM-类加载机制
类加载 前言:为什么需要了解类加载?什么是类加载?生命周期概览类加载过程详解3.1 加载 (Loading)3.2 连接 (Linking)3.2.1 验证 (Verification)3.2.2 准备 (Preparation)3.2.3 解析 (Resolution) 3.3 初始化 (Initialization)3.3.1 <clini…...

【小白福音】SFTP限制权限登录
下面以在 Linux 环境(例如 Ubuntu 或 CentOS)上配置 SFTP chroot 为例,给出详细的步骤说明。即使你不熟悉服务器运维,也可以按照以下步骤进行配置,保证指定的 SFTP 用户只能访问预设目录,而无法触碰其他文件。 目录 一、配置SFTP权限1. 创建专用 SFTP 用户和用户组2. 搭建…...

海量数据笔试题--Top K 高频词汇统计
问题描述: 假设你有一个非常大的文本文件(例如,100GB),文件内容是按行存储的单词(或其他字符串,如 URL、搜索查询词等),单词之间可能由空格或换行符分隔。由于文件巨大&…...

Postman设置环境变量与Token
设置环境变量 设置某个Collection下的变量...

项目中数据结构为什么用数组,不用List
总结 1,从内存和性能角度,数组占用更小的内存(),访问性能更高() 分配效率:数组在内存中是连续分配的一块固定空间 访问速度:直接操作内存,数组的读写操作是…...
)
Linux常见指令介绍下(入门级)
1. head head就和他的名字一样,是显示一个文件头部的内容(会自动排序),默认是打印前10行。 语法:head [参数] [文件] 选项: -n [x] 显示前x行。 2. tail tail 命令从指定点开始将文件写到标准输出.使用t…...

从Kafka读取数据
用Spark-Streaming从Kafka读取数据 在大数据处理领域,Spark-Streaming和Kafka都是明星技术。今天咱们就来聊聊怎么用Spark-Streaming从Kafka读取数据并做处理,就算你是小白,也保证能看懂!先讲讲从Kafka获取数据的两种方式。早期有…...
)
硬件工程师面试常见问题(7)
第三十一问:RTC电路,电池寿命估算 上图可知,该电路有两个供电一个是电池供电,一个是其他供电,已知电池大小为120mAh,该电路在电池供电下吃3uA的电流,计算 120*(10^3)/ 3…...

二分小专题
P1102 A-B 数对 P1102 A-B 数对 暴力枚举还是很好做的,直接上双层循环OK 二分思路:查找边界情况,找出最大下标和最小下标,两者相减1即为答案所求 废话不多说,上代码 //暴力O(n^3) 72pts // #include<bits/stdc.h> // usin…...

Explain详解与索引最佳实践
Explain工具介绍 使用EXPLAIN关键字可以模拟优化器执行SQL语句,分析你的查询语句或是结构的性能瓶颈 在 select 语句之前增加 explain 关键字,MySQL 会在查询上设置一个标记,执行查询会返回执行计划的信息,而不是执行这条SQL 注意…...
)
【Qt6 QML Book 基础】07:布局项 —— 锚定布局与动态交互(附完整可运行代码)
引言 在 QML 界面开发中,** 锚定布局(Anchors)** 是实现响应式设计的核心机制。通过声明式的锚定规则,开发者无需手动计算坐标,即可让元素与父容器或其他元素保持动态位置关联。本文结合官方示例,详细解析…...
(纯命令))
rocky9.4部署k8s群集v1.28.2版本(containerd)(纯命令)
文章目录 前言三个节点的主机名 所有节点操作主机名和ip解析关闭交换分区,关闭防火墙,关闭selinux更换阿里云yum源时间同步修改内核参数修改系统最大打开文件数开启bridge网桥过滤,加载br_netfilter模块,加载配置文件安装ipset及i…...
)
Crawl4AI 部署安装及 n8n 调用,实现自动化工作流(保证好使)
Crawl4AI 部署安装及 n8n 调用,实现自动化工作流(保证好使) 简介 Crawl4AI 的介绍 一、Crawl4AI 的核心功能 二、Crawl4AI vs Firecrawl Crawl4AI 的本地部署 一、前期准备 二、部署步骤 1、检查系统的网络环境 2、下载 Crawl4AI 源…...

onlyoffice8.3.3发布了-豆豆容器市场同步更新ARM64版本
8.3.3 修复内容 文档编辑器 • 修复从右到左(RTL)段落的计算问题 (DocumentServer#2590) • 修复从右到左段落中"项目符号/编号/多级列表"样式缩略图的显示问题 • 修复从右到左段落中编号列表(项目符号)的显示问题 (…...

rabbitmq安装项目集成
使用Docker来安装 1.1.下载镜像 docker pull rabbitmq:3-management 1.2.安装MQ docker run \-e RABBITMQ_DEFAULT_USER=root \-e RABBITMQ_DEFAULT_PASS=123123 \--name mq \--hostname mq1 \-p 15672:15672 \-p 5672:5672 \-d \rabbitmq:3-management 15672:RabbitMQ提供…...

济南国网数字化培训班学习笔记-第二组-3节-电网工程建设项目部门
电网工程建设项目部 组成 监理项目部 履行监理合同,监理单位派驻:负责合同管理,审查,见证,旁站,巡视,验收,控制进度,安全,质量,协调各方 造价…...
安装及配置 --- app笔记)
JDK(java)安装及配置 --- app笔记
JDK官方下载地址:Java Downloads | Oracle 安装好后,配置 “环境变量”: 新建JAVA_HOME变量,值为 jdk 安装 根目录(C:\Program Files\Java\jdk-24) 在path变量最后面,添加 %JAVA_HOME% 新建 CLA…...

【前端】【面试】在前端开发中,如何优化 CSS 以提升页面渲染性能?
题目:在前端开发中,如何优化 CSS 以提升页面渲染性能? 关键词总结 关键词说明选择器优化避免通配符、减少层级深度、防止后代选择器过度嵌套样式规则优化合并重复规则、慎用高成本属性加载与渲染优化关键 CSS 优先加载、合理使用媒体查询文…...

python的mtcnn检测图片中的人脸并标框
python的mtcnn检测图片中的人脸并标框,标记鼻尖位置 import cv2 from mtcnn import MTCNN# 初始化 MTCNN 检测器 # stages:指定检测阶段 # 指定运行设备为CPU detector MTCNN(stages"face_and_landmarks_detection", device"CPU:0"…...

矩阵系统源码搭建账号分组功能开发全流程解析,支持OEM
在短视频矩阵运营场景下,企业和创作者往往管理着数十甚至上百个不同平台的账号,传统的统一管理模式效率低下,难以满足精细化运营需求。矩阵系统的账号分组功能通过对账号进行分类整合,实现差异化管理与精准化操作。本文将从功能需…...

跟着deepseek学golang--认识golang
文章目录 一、Golang核心优势1. 极简部署方式生产案例:依赖管理:容器实践: 2. 静态类型系统类型安全示例:性能优势:代码重构: 3. 语言级并发支持GMP调度模型实例&…...

如何创建极狐GitLab 议题?
极狐GitLab 是 GitLab 在中国的发行版,关于中文参考文档和资料有: 极狐GitLab 中文文档极狐GitLab 中文论坛极狐GitLab 官网 创建议题 (BASIC ALL) 创建议题时,系统会提示您输入议题的字段。 如果您知道要分配给议题的值,则可…...

制造工厂如何借助电子看板实现高效生产管控
在当今高度竞争的制造业环境中,许多企业正面临着严峻的管理和生产挑战。首先,管理流程落后,大量工作仍依赖"人治"方式,高层管理者理论知识薄弱且不愿听取专业意见。其次,生产过程控制能力不足,导…...
