Python----深度学习(神经网络的过拟合解决方案)
一、正则化
1.1、正则化
正则化是一种用于控制模型复杂度的技术。它通过在损失函数中添加额外的项(正则 化项)来降低模型的复杂度,以防止过拟合。
在机器学习中,模型的目标是在训练数据上获得较好的拟合效果。然而,过于复杂的 模型可能会在训练数据上表现良好,但在未见过的数据上表现较差,这种现象称为过 拟合。为了避免过拟合,正则化技术被引入。

1.2、为什么加入正则化可以解决过拟合?
加入正则化之后,想要损失函数尽可能的小,不仅仅要让原来的MSE的 值尽可能的小,还需要让后面正则化项的值尽可能的小。 要让正则化项的的值尽可能的小,那么就要使的参数 尽可能的小。
参数 小和解决过拟合的关系:
过拟合的实质是模型过于复杂或者训练样本较少,也可以理解为:针对当前 样本,模型过于复杂。 模型的复杂程度是由参数的个数和参数大小范围决定的,那么如果降低参数 的大 小范围,就可以降低模型的复杂度,因此可以用来解决过拟合问题。
1.3、正则化的基本思想
正则化的基本思想是在损失函数中引入一个额外的项,该项与模型的复杂度相关。这 个额外的项可以是参数的平方和(L2正则化),参数的绝对值和(L1正则化)或其 他形式的复杂度度量。通过调整正则化参数,可以控制正则化项在损失函数中的权 重。
正则化的目的是通过在损失函数中添加一个正则项(通常是权重的 L1 或 L2 范 数),以惩罚模型的复杂度,从而避免过拟合问题。
1.4、L1正则化和L2正则化


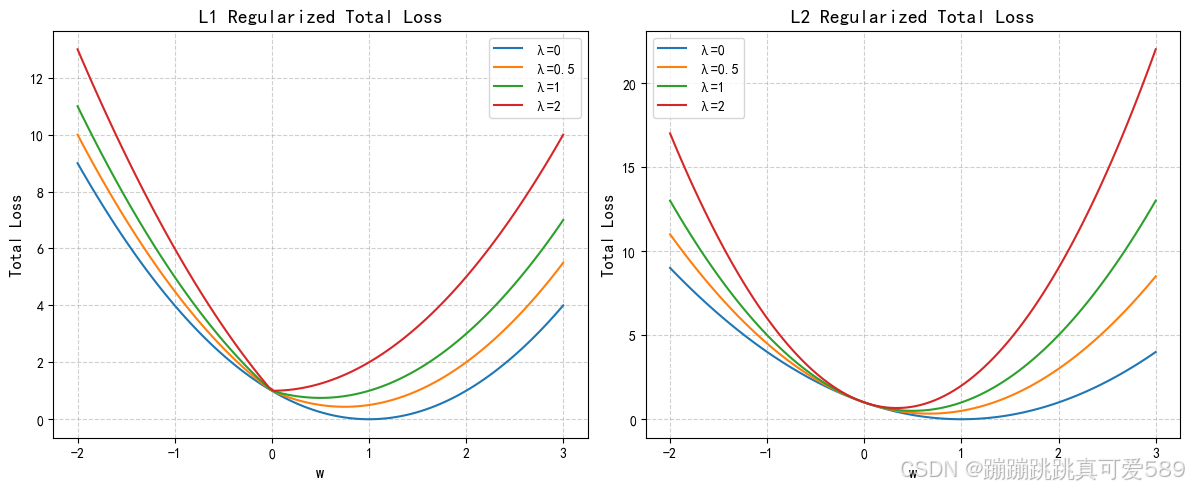
| 特性 | L1正则化 | L2正则化 |
|---|---|---|
| 稀疏性 | 产生稀疏解(部分权重为零) | 不产生稀疏解(权重接近零) |
| 优化特性 | 在零点不可导,需特殊处理 | 在零点可导,优化稳定 |
| 几何形状(2D) | 菱形 | 圆形 |
| 应用场景 | 特征选择、高维稀疏数据 | 防止过拟合、平滑权重分布 |
二、Dropout
Dropout是一种在神经网络训练过程中使用的正则化技术,旨在减少过拟合现象。其 思想是在每次训练迭代中,随机地将一部分神经元的输出置为0,即将其“丢弃”,从 而降低神经网络对特定神经元的依赖性,减少神经网络的复杂度,增强神经网络的泛 化能力。

import torch # 创建一个Dropout层,丢弃概率为0.2
m = torch.nn.Dropout(p=0.2) # 生成一个形状为(10, 1)的随机输入张量
input = torch.randn(10, 1)
print("输入张量:")
print(input) # 将Dropout层应用于输入张量
output = m(input)
print("应用Dropout后的输出:")
print(output) def dropout_layer(X, dropout): # 确保dropout概率在0和1之间 assert 0 <= dropout <= 1 # 如果dropout为1,返回与X形状相同的全零张量 if dropout == 1: return torch.zeros_like(X) # 如果dropout为0,返回原始张量X if dropout == 0: return X # 创建一个掩码,其中值大于指定的dropout概率 mask = (X > dropout).float() print("掩码张量:") print(mask) # 通过掩码调整输出,并按dropout概率进行缩放 return mask * X / (1.0 - dropout) # 将自定义dropout层应用于输入张量
out = dropout_layer(input, 0.2)
print("自定义dropout层的输出:")
print(out) Dropout为什么能够解决过拟合:
(1)减少过拟合: 在标准的神经网络中,网络可能会过度依赖于一些特定的神经 元,导致对训练数据的过拟合。Dropout通过随机丢弃神经元,迫使网络学习对于任 何单个神经元的变化都要更加鲁棒的特征表示,从而减少了对训练数据的过度拟合。
(2)取平均的作用: 在训练过程中,通过丢弃随机的神经元,每次前向传播都相当 于在训练不同的子网络。在测试阶段,不再进行Dropout,但是通过保留所有的权 重,网络结构变得更加完整。因此,可以看作是在多个不同的子网络中进行了训练, 最终的预测结果相当于对这些子网络的输出取平均。这种“综合取平均”的策略有助于 减轻过拟合,因为一些互为反向的拟合会相互抵消。
三、设计思路

输入数据
class1_points = np.array([[-0.7, 0.7], [3.9, 1.5], [1.7, 2.2], [1.9, -2.4], [0.9, 1.4], [4.2, 0.9], [1.7, 0.7], [0.2, -0.2], [3.1, -0.4],[-0.2, -0.9], [1.7, 0.2], [-0.6, -3.9], [-1.8, -4.0], [0.7, 3.8], [-0.7, -3.3], [0.8, 1.8], [-0.5, 1.5],[-0.6, -3.6], [-3.1, -3.0], [2.1, -2.5], [-2.5, -3.4], [-2.6, -0.8], [-0.2, 0.9], [-3.0, 3.3], [-0.7, 0.2],[0.3, 3.0], [0.6, 1.9], [-4.0, 2.4], [1.9, -2.2], [1.0, 0.3], [-0.9, -0.7], [-3.7, 0.6], [-2.7, -1.5], [0.9, -0.3],[0.8, -0.2], [-0.4, -4.4], [-0.3, 0.8], [4.1, 1.0], [-2.5, -3.5], [-0.8, 0.3], [0.6, 0.6], [2.6, -1.0], [1.8, 0.4],[1.5, -1.0], [3.2, 1.1], [3.3, -2.5], [-3.8, 2.5], [3.1, -0.9], [3.4, -1.1], [0.3, 0.8], [-0.1, 2.9], [-2.8, 1.9],[2.8, -3.3], [-1.0, 3.1], [-0.8, -0.6], [-2.5, -1.5], [0.3, 0.2], [-1.0, -2.9], [0.7, 0.2], [-0.5, 0.9],[-0.8, 0.7], [4.1, 0.5], [2.8, 2.3], [-3.9, 0.1], [2.2, -1.4], [-0.7, -3.5], [1.0, 1.2], [-0.7, -4.0], [1.3, 0.6],[-0.1, 3.3], [0.0, -0.3], [1.8, -3.0], [0.6, 0.0], [3.6, -2.8], [-3.9, -0.9], [-4.3, -0.9], [0.1, -0.8],[-1.6, -2.7], [-1.8, -3.3], [1.7, -3.5], [3.6, -3.1], [-2.4, 2.5], [-1.0, 1.8], [3.9, 2.5], [-3.9, -1.3],[3.4, 1.6], [-0.1, -0.6], [-3.7, -1.3], [-0.3, 3.4], [-3.7, -1.7], [4.0, 1.1], [3.4, 0.2], [0.1, -1.6],[-1.2, -0.5], [2.4, 1.7], [-4.4, -0.5], [-0.2, -3.6], [-0.8, 0.4], [-1.5, -2.2], [3.9, 2.5], [4.4, 1.4],[-3.5, -1.1], [-0.7, 1.5], [-3.0, -2.6], [0.2, -3.5], [0.0, 1.2], [-4.3, 0.1], [-1.8, 2.8], [1.1, -2.5],[0.2, 4.3], [-3.9, 2.2], [1.0, 1.6], [4.5, 0.2], [3.9, -1.6], [-0.4, -0.5], [0.3, -0.4], [-3.2, 1.7], [2.0, 4.1],[2.5, 2.2], [-1.1, -0.3], [-3.7, -1.9], [1.5, -1.1], [-2.1, -1.9], [-0.1, 4.5], [3.8, -0.3], [-0.9, -3.8],[-2.9, -1.6], [1.0, -1.2], [0.7, 0.0], [-0.8, 3.3], [-2.8, 3.1], [0.4, -3.2], [4.6, 1.0], [2.5, 3.1], [4.2, 0.8],[3.6, 1.8], [1.4, -3.0], [-0.4, -1.4], [-4.1, 1.1], [1.1, -0.2], [-2.9, -0.0], [-3.5, 1.3], [-1.4, 0.0],[-3.7, 2.2], [-2.9, 2.8], [1.7, 0.4], [-0.8, -0.6], [2.9, 1.1], [-2.3, 3.1], [-2.9, -2.0], [-2.7, -0.4],[2.6, -2.4], [-1.7, -2.8], [1.2, 3.1], [3.8, 1.3], [0.1, 1.9], [-0.5, -1.0], [0.0, -0.5], [3.9, -0.7],[-3.7, -2.5], [-3.1, 2.7], [-0.9, -1.0], [-0.7, -0.8], [-0.4, -0.1], [1.5, 1.0], [-2.6, 1.9], [-0.8, 1.7],[0.8, 1.8], [2.0, 3.6], [3.2, 1.4], [2.3, 1.4], [4.9, 0.5], [2.2, 1.8], [-1.4, -2.7], [3.1, 1.1], [-1.0, 3.8],[-0.4, -1.1], [3.3, 1.1], [2.2, -3.9], [1.0, 1.2], [2.6, 3.2], [-0.6, -3.0], [-1.9, -2.8], [1.2, -1.2],[-0.4, -2.7], [1.1, -4.3], [0.3, -0.8], [-1.0, -0.4], [-1.1, -0.2], [0.1, 1.2], [0.9, 0.6], [-2.7, 1.6],[1.0, -0.7], [0.3, -4.2], [-2.1, 3.2], [3.4, -1.2], [2.5, -4.0], [1.0, -0.8], [1.0, -0.9], [0.1, -0.6]])
class2_points = np.array([[-3.0, -3.8], [4.4, 2.5], [2.6, 4.1], [3.7, -2.7], [-3.7, -2.9], [5.3, 0.3], [3.9, 2.9], [-2.7, -4.5], [5.4, 0.2],[3.0, 4.8], [-4.2, -1.3], [-2.1, -5.4], [-3.2, -4.6], [0.7, 4.5], [-1.4, -5.7], [0.5, 5.9], [-2.1, 4.0],[-0.1, -5.1], [-3.4, -4.7], [3.3, -4.7], [-2.7, -4.1], [-4.5, -2.0], [4.3, 2.9], [-3.6, 4.0], [-0.5, 5.5],[0.2, 5.2], [5.3, -0.9], [-4.5, 3.6], [3.4, -2.8], [-3.4, -3.7], [1.6, -5.5], [-5.9, -0.1], [-4.8, -2.5],[-5.5, 0.3], [1.6, 4.4], [-0.9, -5.3], [-1.0, 5.4], [4.9, 0.8], [-3.1, -4.0], [2.3, 4.7], [4.0, -1.6], [4.9, -1.5],[4.2, -2.5], [-3.5, 3.7], [4.7, 0.5], [5.3, -2.6], [-5.0, 2.4], [5.5, -1.2], [5.6, -1.3], [3.3, -4.3], [-1.3, 4.4],[-4.1, 3.6], [3.3, -4.5], [-2.3, 5.2], [2.6, 4.6], [-4.4, -1.6], [4.7, -2.0], [-1.7, -4.9], [-5.1, -2.4],[4.5, 3.2], [-3.9, -3.4], [6.0, -0.4], [3.5, 4.3], [-4.9, -0.6], [3.3, -3.2], [-0.3, -4.8], [-1.6, -4.7],[-1.4, -4.6], [-3.1, 3.8], [-1.4, 4.9], [1.8, -4.5], [2.2, -5.5], [3.1, -3.4], [4.7, -2.8], [-5.3, -0.4],[-6.0, -0.1], [1.4, -4.5], [-3.1, -4.3], [-1.8, -5.7], [1.7, -5.6], [4.5, -3.7], [-2.6, 4.3], [-3.4, 3.4],[4.7, 3.1], [-5.2, -2.8], [5.4, 1.2], [-5.4, 1.2], [-4.9, -1.3], [-1.3, 5.6], [-4.1, -2.6], [5.0, 1.0], [5.2, 1.2],[2.4, -4.9], [-3.2, 3.8], [3.3, 3.4], [-5.5, -0.8], [0.6, -5.0], [1.2, 5.4], [-3.4, -3.3], [4.6, 2.8], [5.2, 1.7],[-4.4, -0.9], [-5.0, -1.3], [-3.1, -3.6], [-0.7, -4.5], [5.9, -0.9], [-5.1, -0.5], [-2.6, 5.2], [1.4, -4.8],[-0.7, 5.6], [-5.3, 2.1], [4.9, 2.6], [5.3, 0.9], [5.1, -1.2], [2.7, -4.4], [-2.0, -5.6], [-4.9, 3.2], [2.8, 5.3],[2.6, 3.9], [-0.0, 5.7], [-5.7, -1.8], [-1.1, -4.7], [-2.4, -3.8], [-1.1, 5.6], [5.3, -1.5], [-0.4, -5.8],[-4.5, -1.6], [-4.4, -3.7], [-4.3, 2.4], [0.1, 4.8], [-3.0, 3.8], [0.3, -5.8], [5.6, 0.5], [4.1, 3.6], [5.0, 1.5],[5.7, 1.5], [3.2, -4.1], [-1.7, -5.6], [-5.3, 0.9], [4.3, 3.0], [-5.4, 0.3], [-5.0, 0.8], [2.7, 5.1], [-5.0, 2.2],[-4.0, 3.0], [-4.4, -3.9], [-3.5, -3.9], [5.3, 1.5], [-4.2, 4.2], [-3.9, -4.0], [-4.7, -0.1], [3.7, -4.7],[-3.0, -4.7], [2.7, 4.4], [4.3, 2.0], [-3.6, -4.5], [5.5, 0.9], [-4.7, -2.8], [5.5, -2.2], [-5.1, -2.6],[-3.6, 3.1], [-3.2, -4.0], [-4.8, 1.3], [-5.5, -1.6], [4.1, -1.6], [-4.2, 3.6], [5.6, -1.4], [4.9, -3.3],[1.7, 4.9], [5.3, 2.5], [3.8, 2.8], [5.8, 0.7], [3.9, 2.6], [-2.1, -4.8], [5.2, 2.5], [-2.0, 4.3], [2.8, -4.1],[5.6, 0.8], [2.2, -5.2], [-1.1, 5.5], [4.2, 3.8], [-1.8, -5.2], [-3.4, -3.6], [3.7, -3.6], [-0.5, -4.8],[1.9, -5.6], [-1.1, 5.4], [2.3, 4.7], [0.0, -5.4], [2.1, -5.6], [4.8, -0.3], [-4.7, 2.9], [-3.8, 3.9], [0.9, -5.5],[-2.3, 3.6], [5.3, -2.5], [3.7, -4.6], [-5.0, 2.4], [0.0, -5.7], [0.2, -5.9]])# 合并两类点
points = np.concatenate((class1_points, class2_points))
# 标签 0表示类别1,1表示类别2
labels1 = np.zeros(len(class1_points))
labels2 = np.ones(len(class2_points))labels = np.concatenate((labels1, labels2))构建模型
class ModelClass(nn.Module):def __init__(self):super().__init__()# 定义网络层结构:self.layer1 = nn.Linear(2, 16) # 输入层(2维特征)→ 16维隐藏层self.layer2 = nn.Linear(16, 48) # 16维 → 48维隐藏层self.layer3 = nn.Linear(48, 32) # 48维 → 32维隐藏层self.layer4 = nn.Linear(32, 2) # 32维 → 输出层(2类概率)# 定义Dropout层(随机丢弃神经元防止过拟合)self.dropout1 = nn.Dropout(p=0.1) # 丢弃概率10%self.dropout2 = nn.Dropout(p=0.1)self.dropout3 = nn.Dropout(p=0.1)def forward(self, x):x = torch.relu(self.layer1(x)) # 第一层后接ReLU激活函数x = self.dropout1(x) # 应用Dropoutx = torch.relu(self.layer2(x)) # 第二层 + ReLUx = self.dropout2(x)x = torch.relu(self.layer3(x)) # 第三层 + ReLUx = self.dropout3(x)x=self.layer4(x) # 输出层Softmax获取概率return x# 初始化模型实例
model = ModelClass()构建损失函数和优化器
criterion = nn.CrossEntropyLoss() # 交叉熵损失函数(多分类任务常用)
optimizer = optim.Adam(model.parameters(), lr=0.01) # Adam优化器,学习率0.01
训练模型
num_iterations = 2000 # 总迭代次数
batch_size = 32 # 批量大小for n in range(num_iterations + 1):model.train() # 设置模型为训练模式(启用Dropout)# 分批训练for batch_start in range(0, len(points), batch_size):# 获取当前批次的数据和标签batch_inputs = torch.tensor(points[batch_start:batch_start + batch_size], dtype=torch.float32)batch_labels = torch.tensor(labels[batch_start:batch_start + batch_size], dtype=torch.long)# 前向传播outputs = model(batch_inputs)loss = criterion(outputs, batch_labels) # 计算损失# 反向传播与优化optimizer.zero_grad() # 清空梯度缓存loss.backward() # 反向传播计算梯度optimizer.step() # 更新权重参数# 每隔100次迭代可视化结果if n % 100 == 0 or n == 1:print(n,loss.item())可视化
num_iterations = 2000 # 总迭代次数
batch_size = 32 # 批量大小for n in range(num_iterations + 1):model.train() # 设置模型为训练模式(启用Dropout)# 分批训练for batch_start in range(0, len(points), batch_size):# 获取当前批次的数据和标签batch_inputs = torch.tensor(points[batch_start:batch_start + batch_size], dtype=torch.float32)batch_labels = torch.tensor(labels[batch_start:batch_start + batch_size], dtype=torch.long)# 前向传播outputs = model(batch_inputs)loss = criterion(outputs, batch_labels) # 计算损失# 反向传播与优化optimizer.zero_grad() # 清空梯度缓存loss.backward() # 反向传播计算梯度optimizer.step() # 更新权重参数# 每隔100次迭代可视化结果if n % 100 == 0 or n == 1:print(n,loss.item())model.eval() # 设置模型为评估模式(关闭Dropout)with torch.no_grad(): # 关闭梯度计算# 预测所有网格点的类别概率grid_points_tensor = torch.tensor(grid_points, dtype=torch.float32)Z = model(grid_points_tensor).numpy()Z = Z[:, 1] # 获取类别2的概率值# 调整形状以匹配网格矩阵Z = Z.reshape(xx.shape)# 绘制分类结果plt.cla() # 清空当前图像plt.scatter(class1_points[:, 0], class1_points[:, 1], c='blue', label='Class 1')plt.scatter(class2_points[:, 0], class2_points[:, 1], c='red', label='Class 2')plt.contour(xx, yy, Z, levels=[0.5], colors='black') # 绘制0.5概率等高线作为决策边界plt.title(f"Epochs: {n}")plt.show() # 显示最终图像完整代码
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt# --------------------------------------------- 数据准备部分 ---------------------------------------------
# 类别1的二维坐标点(蓝色点)
class1_points = np.array([[-0.7, 0.7], [3.9, 1.5], [1.7, 2.2], [1.9, -2.4], [0.9, 1.4], [4.2, 0.9], [1.7, 0.7], [0.2, -0.2], [3.1, -0.4],[-0.2, -0.9], [1.7, 0.2], [-0.6, -3.9], [-1.8, -4.0], [0.7, 3.8], [-0.7, -3.3], [0.8, 1.8], [-0.5, 1.5],[-0.6, -3.6], [-3.1, -3.0], [2.1, -2.5], [-2.5, -3.4], [-2.6, -0.8], [-0.2, 0.9], [-3.0, 3.3], [-0.7, 0.2],[0.3, 3.0], [0.6, 1.9], [-4.0, 2.4], [1.9, -2.2], [1.0, 0.3], [-0.9, -0.7], [-3.7, 0.6], [-2.7, -1.5], [0.9, -0.3],[0.8, -0.2], [-0.4, -4.4], [-0.3, 0.8], [4.1, 1.0], [-2.5, -3.5], [-0.8, 0.3], [0.6, 0.6], [2.6, -1.0], [1.8, 0.4],[1.5, -1.0], [3.2, 1.1], [3.3, -2.5], [-3.8, 2.5], [3.1, -0.9], [3.4, -1.1], [0.3, 0.8], [-0.1, 2.9], [-2.8, 1.9],[2.8, -3.3], [-1.0, 3.1], [-0.8, -0.6], [-2.5, -1.5], [0.3, 0.2], [-1.0, -2.9], [0.7, 0.2], [-0.5, 0.9],[-0.8, 0.7], [4.1, 0.5], [2.8, 2.3], [-3.9, 0.1], [2.2, -1.4], [-0.7, -3.5], [1.0, 1.2], [-0.7, -4.0], [1.3, 0.6],[-0.1, 3.3], [0.0, -0.3], [1.8, -3.0], [0.6, 0.0], [3.6, -2.8], [-3.9, -0.9], [-4.3, -0.9], [0.1, -0.8],[-1.6, -2.7], [-1.8, -3.3], [1.7, -3.5], [3.6, -3.1], [-2.4, 2.5], [-1.0, 1.8], [3.9, 2.5], [-3.9, -1.3],[3.4, 1.6], [-0.1, -0.6], [-3.7, -1.3], [-0.3, 3.4], [-3.7, -1.7], [4.0, 1.1], [3.4, 0.2], [0.1, -1.6],[-1.2, -0.5], [2.4, 1.7], [-4.4, -0.5], [-0.2, -3.6], [-0.8, 0.4], [-1.5, -2.2], [3.9, 2.5], [4.4, 1.4],[-3.5, -1.1], [-0.7, 1.5], [-3.0, -2.6], [0.2, -3.5], [0.0, 1.2], [-4.3, 0.1], [-1.8, 2.8], [1.1, -2.5],[0.2, 4.3], [-3.9, 2.2], [1.0, 1.6], [4.5, 0.2], [3.9, -1.6], [-0.4, -0.5], [0.3, -0.4], [-3.2, 1.7], [2.0, 4.1],[2.5, 2.2], [-1.1, -0.3], [-3.7, -1.9], [1.5, -1.1], [-2.1, -1.9], [-0.1, 4.5], [3.8, -0.3], [-0.9, -3.8],[-2.9, -1.6], [1.0, -1.2], [0.7, 0.0], [-0.8, 3.3], [-2.8, 3.1], [0.4, -3.2], [4.6, 1.0], [2.5, 3.1], [4.2, 0.8],[3.6, 1.8], [1.4, -3.0], [-0.4, -1.4], [-4.1, 1.1], [1.1, -0.2], [-2.9, -0.0], [-3.5, 1.3], [-1.4, 0.0],[-3.7, 2.2], [-2.9, 2.8], [1.7, 0.4], [-0.8, -0.6], [2.9, 1.1], [-2.3, 3.1], [-2.9, -2.0], [-2.7, -0.4],[2.6, -2.4], [-1.7, -2.8], [1.2, 3.1], [3.8, 1.3], [0.1, 1.9], [-0.5, -1.0], [0.0, -0.5], [3.9, -0.7],[-3.7, -2.5], [-3.1, 2.7], [-0.9, -1.0], [-0.7, -0.8], [-0.4, -0.1], [1.5, 1.0], [-2.6, 1.9], [-0.8, 1.7],[0.8, 1.8], [2.0, 3.6], [3.2, 1.4], [2.3, 1.4], [4.9, 0.5], [2.2, 1.8], [-1.4, -2.7], [3.1, 1.1], [-1.0, 3.8],[-0.4, -1.1], [3.3, 1.1], [2.2, -3.9], [1.0, 1.2], [2.6, 3.2], [-0.6, -3.0], [-1.9, -2.8], [1.2, -1.2],[-0.4, -2.7], [1.1, -4.3], [0.3, -0.8], [-1.0, -0.4], [-1.1, -0.2], [0.1, 1.2], [0.9, 0.6], [-2.7, 1.6],[1.0, -0.7], [0.3, -4.2], [-2.1, 3.2], [3.4, -1.2], [2.5, -4.0], [1.0, -0.8], [1.0, -0.9], [0.1, -0.6]])
class2_points = np.array([[-3.0, -3.8], [4.4, 2.5], [2.6, 4.1], [3.7, -2.7], [-3.7, -2.9], [5.3, 0.3], [3.9, 2.9], [-2.7, -4.5], [5.4, 0.2],[3.0, 4.8], [-4.2, -1.3], [-2.1, -5.4], [-3.2, -4.6], [0.7, 4.5], [-1.4, -5.7], [0.5, 5.9], [-2.1, 4.0],[-0.1, -5.1], [-3.4, -4.7], [3.3, -4.7], [-2.7, -4.1], [-4.5, -2.0], [4.3, 2.9], [-3.6, 4.0], [-0.5, 5.5],[0.2, 5.2], [5.3, -0.9], [-4.5, 3.6], [3.4, -2.8], [-3.4, -3.7], [1.6, -5.5], [-5.9, -0.1], [-4.8, -2.5],[-5.5, 0.3], [1.6, 4.4], [-0.9, -5.3], [-1.0, 5.4], [4.9, 0.8], [-3.1, -4.0], [2.3, 4.7], [4.0, -1.6], [4.9, -1.5],[4.2, -2.5], [-3.5, 3.7], [4.7, 0.5], [5.3, -2.6], [-5.0, 2.4], [5.5, -1.2], [5.6, -1.3], [3.3, -4.3], [-1.3, 4.4],[-4.1, 3.6], [3.3, -4.5], [-2.3, 5.2], [2.6, 4.6], [-4.4, -1.6], [4.7, -2.0], [-1.7, -4.9], [-5.1, -2.4],[4.5, 3.2], [-3.9, -3.4], [6.0, -0.4], [3.5, 4.3], [-4.9, -0.6], [3.3, -3.2], [-0.3, -4.8], [-1.6, -4.7],[-1.4, -4.6], [-3.1, 3.8], [-1.4, 4.9], [1.8, -4.5], [2.2, -5.5], [3.1, -3.4], [4.7, -2.8], [-5.3, -0.4],[-6.0, -0.1], [1.4, -4.5], [-3.1, -4.3], [-1.8, -5.7], [1.7, -5.6], [4.5, -3.7], [-2.6, 4.3], [-3.4, 3.4],[4.7, 3.1], [-5.2, -2.8], [5.4, 1.2], [-5.4, 1.2], [-4.9, -1.3], [-1.3, 5.6], [-4.1, -2.6], [5.0, 1.0], [5.2, 1.2],[2.4, -4.9], [-3.2, 3.8], [3.3, 3.4], [-5.5, -0.8], [0.6, -5.0], [1.2, 5.4], [-3.4, -3.3], [4.6, 2.8], [5.2, 1.7],[-4.4, -0.9], [-5.0, -1.3], [-3.1, -3.6], [-0.7, -4.5], [5.9, -0.9], [-5.1, -0.5], [-2.6, 5.2], [1.4, -4.8],[-0.7, 5.6], [-5.3, 2.1], [4.9, 2.6], [5.3, 0.9], [5.1, -1.2], [2.7, -4.4], [-2.0, -5.6], [-4.9, 3.2], [2.8, 5.3],[2.6, 3.9], [-0.0, 5.7], [-5.7, -1.8], [-1.1, -4.7], [-2.4, -3.8], [-1.1, 5.6], [5.3, -1.5], [-0.4, -5.8],[-4.5, -1.6], [-4.4, -3.7], [-4.3, 2.4], [0.1, 4.8], [-3.0, 3.8], [0.3, -5.8], [5.6, 0.5], [4.1, 3.6], [5.0, 1.5],[5.7, 1.5], [3.2, -4.1], [-1.7, -5.6], [-5.3, 0.9], [4.3, 3.0], [-5.4, 0.3], [-5.0, 0.8], [2.7, 5.1], [-5.0, 2.2],[-4.0, 3.0], [-4.4, -3.9], [-3.5, -3.9], [5.3, 1.5], [-4.2, 4.2], [-3.9, -4.0], [-4.7, -0.1], [3.7, -4.7],[-3.0, -4.7], [2.7, 4.4], [4.3, 2.0], [-3.6, -4.5], [5.5, 0.9], [-4.7, -2.8], [5.5, -2.2], [-5.1, -2.6],[-3.6, 3.1], [-3.2, -4.0], [-4.8, 1.3], [-5.5, -1.6], [4.1, -1.6], [-4.2, 3.6], [5.6, -1.4], [4.9, -3.3],[1.7, 4.9], [5.3, 2.5], [3.8, 2.8], [5.8, 0.7], [3.9, 2.6], [-2.1, -4.8], [5.2, 2.5], [-2.0, 4.3], [2.8, -4.1],[5.6, 0.8], [2.2, -5.2], [-1.1, 5.5], [4.2, 3.8], [-1.8, -5.2], [-3.4, -3.6], [3.7, -3.6], [-0.5, -4.8],[1.9, -5.6], [-1.1, 5.4], [2.3, 4.7], [0.0, -5.4], [2.1, -5.6], [4.8, -0.3], [-4.7, 2.9], [-3.8, 3.9], [0.9, -5.5],[-2.3, 3.6], [5.3, -2.5], [3.7, -4.6], [-5.0, 2.4], [0.0, -5.7], [0.2, -5.9]])# 合并两类点
points = np.concatenate((class1_points, class2_points))
# 标签 0表示类别1,1表示类别2
labels1 = np.zeros(len(class1_points))
labels2 = np.ones(len(class2_points))labels = np.concatenate((labels1, labels2))# --------------------------------------------- 模型定义部分 ---------------------------------------------
class ModelClass(nn.Module):def __init__(self):super().__init__()# 定义网络层结构:self.layer1 = nn.Linear(2, 16) # 输入层(2维特征)→ 16维隐藏层self.layer2 = nn.Linear(16, 48) # 16维 → 48维隐藏层self.layer3 = nn.Linear(48, 32) # 48维 → 32维隐藏层self.layer4 = nn.Linear(32, 2) # 32维 → 输出层(2类概率)# 定义Dropout层(随机丢弃神经元防止过拟合)self.dropout1 = nn.Dropout(p=0.1) # 丢弃概率10%self.dropout2 = nn.Dropout(p=0.1)self.dropout3 = nn.Dropout(p=0.1)def forward(self, x):x = torch.relu(self.layer1(x)) # 第一层后接ReLU激活函数x = self.dropout1(x) # 应用Dropoutx = torch.relu(self.layer2(x)) # 第二层 + ReLUx = self.dropout2(x)x = torch.relu(self.layer3(x)) # 第三层 + ReLUx = self.dropout3(x)x=self.layer4(x) # 输出层Softmax获取概率return x# 初始化模型实例
model = ModelClass()
# --------------------------------------------- 训练配置部分 ---------------------------------------------
criterion = nn.CrossEntropyLoss() # 交叉熵损失函数(多分类任务常用)
optimizer = optim.Adam(model.parameters(), lr=0.01) # Adam优化器,学习率0.01# 生成网格点用于绘制决策边界
x_min, x_max = points[:, 0].min() - 1, points[:, 0].max() + 1
y_min, y_max = points[:, 1].min() - 1, points[:, 1].max() + 1
step_size = 0.1
xx, yy = np.meshgrid(np.arange(x_min, x_max, step_size),np.arange(y_min, y_max, step_size))
grid_points = np.c_[xx.ravel(), yy.ravel()] # 生成网格坐标矩阵# --------------------------------------------- 训练循环部分 ---------------------------------------------
num_iterations = 2000 # 总迭代次数
batch_size = 32 # 批量大小for n in range(num_iterations + 1):model.train() # 设置模型为训练模式(启用Dropout)# 分批训练for batch_start in range(0, len(points), batch_size):# 获取当前批次的数据和标签batch_inputs = torch.tensor(points[batch_start:batch_start + batch_size], dtype=torch.float32)batch_labels = torch.tensor(labels[batch_start:batch_start + batch_size], dtype=torch.long)# 前向传播outputs = model(batch_inputs)loss = criterion(outputs, batch_labels) # 计算损失# 反向传播与优化optimizer.zero_grad() # 清空梯度缓存loss.backward() # 反向传播计算梯度optimizer.step() # 更新权重参数# 每隔100次迭代可视化结果if n % 100 == 0 or n == 1:print(n,loss.item())model.eval() # 设置模型为评估模式(关闭Dropout)with torch.no_grad(): # 关闭梯度计算# 预测所有网格点的类别概率grid_points_tensor = torch.tensor(grid_points, dtype=torch.float32)Z = model(grid_points_tensor).numpy()Z = Z[:, 1] # 获取类别2的概率值# 调整形状以匹配网格矩阵Z = Z.reshape(xx.shape)# 绘制分类结果plt.cla() # 清空当前图像plt.scatter(class1_points[:, 0], class1_points[:, 1], c='blue', label='Class 1')plt.scatter(class2_points[:, 0], class2_points[:, 1], c='red', label='Class 2')plt.contour(xx, yy, Z, levels=[0.5], colors='black') # 绘制0.5概率等高线作为决策边界plt.title(f"Epochs: {n}")plt.show() # 显示最终图像相关文章:
)
Python----深度学习(神经网络的过拟合解决方案)
一、正则化 1.1、正则化 正则化是一种用于控制模型复杂度的技术。它通过在损失函数中添加额外的项(正则 化项)来降低模型的复杂度,以防止过拟合。 在机器学习中,模型的目标是在训练数据上获得较好的拟合效果。然而,过…...

【金仓数据库征文】从 HTAP 到 AI 加速,KingbaseES 的未来之路
国产数据库早已实现 “可替代”,但要真正与国际头部厂商掰手腕,必须在 HTAP(Hybrid‑Transaction/Analytical Processing)与 AI 加速 两条技术赛道上实现跨越。KingbaseES 自 V8R3 调整为多进程架构后,历经 V8R6、KSOn…...

创建第一个Spring Boot项目
什么是Spring Boot 随着Spring的快速发展,项目中的XML文件越来越多,繁琐的配置以及,整合第三方框架的配置问题,导致大大增加了开发和部署的效率,使开发者无法专心于业务的开发。Spring Boot就相当于使Spring框架的脚手…...

Java—— 正则表达式 练习
需求: 请编写正则表达式验证用户输入的手机号码是否满足要求。 请编写正则表达式验证用户输入的邮箱号是否满足要求。 请编写正则表达式验证用户输入的电话号码是否满足要求。 验证手机号码 13112345678 13712345667 13945679027 139456790271 验证座机电话号码 02…...

Linux[指令与权限]
Linux指令与权限 Linux环境中,打包文件有多种 tar (打包/解包) 指令 tar -czvf 文件要打包到的位置 文件(打包并压缩到) tar -xzvf 文件(在当前目录下解压) tar选项 -c创建压缩文件 -z使用gzip属性压缩 -v展现压缩过程 -f后面使用新建文档名 -x不要新建,解压 -C 文件…...

MySQL数据库精研之旅第十期:打造高效联合查询的实战宝典
专栏:MySQL数据库成长记 个人主页:手握风云 目录 一、简介 1.1. 为什么要使用联合查询 1.2. 多表联合查询时的计算 1.3. 示例 二、内连接 2.1. 语法 2.2. 示例 三、外连接 4.1. 语法 4.2. 示例 一、简介 1.1. 为什么要使用联合查询 一次查询需…...

【Redis】集合类型Set 常用命令详解
1. sadd - 添加 语法:sadd key value > sadd testset A 1 > sadd testset B 1 > sadd testset C 1 > sadd testset C # set的值不能重复 0 > smembers set1 # 查询指定set的所有值,乱序 1) "B" 2) "A" 3) "C&qu…...

React 5 种组件提取思路与实践
在开发时,经常遇到一些高度重复但略有差异的 UI 模式,此时我们当然会把组件提取出去,但是组件提取的方式有很多,怎么根据不同场景选取合适的方式呢?尤其时在复杂的业务场景中,组件提取的思路影响着着代码的可维护性、可读性以及扩展性。本文将以一个[详情]组件为例,探讨…...

第十五届蓝桥杯 2024 C/C++组 合法密码
目录 题目: 题目描述: 题目链接: 思路: substr函数: 思路详解: 代码: 代码详解; 题目: 题目描述: 题目链接: P10906 [蓝桥杯 2024 国 B] 合法密码 -…...

云原生时代的双轮驱动
在当今数字化浪潮汹涌澎湃的时代,企业 IT 主管、CIO、CTO 们肩负着引领企业乘风破浪、实现数字化转型的重任。而主数据平台与数据中台,宛如企业数字化征程中的双引擎,为企业发展注入强劲动力。 一、主数据与数据中台:企业数据世界…...
定时器TIMER详解及实战含源码)
GD32F407单片机开发入门(六)定时器TIMER详解及实战含源码
文章目录 一.概要二.通用定时器内部结构1.时基单元2.时钟源3.输入捕获4.输出比较 三.通用定时器内部特色四.TIME定时器1ms中断例程五.工程源代码下载六.小结 一.概要 定时器就是计数器,应用在我们生活的方方面面,比如有闹钟、计时器等。在GD32F407VET6定…...

时序数据库 TDengine 助力石油石化业务, 平滑接替 Oracle 数据库
小T导读:胜软科技在石油石化行业中选择使用 TDengine 处理时序数据,不仅显著降低了运维数据库的成本,也大幅减少了存储空间的占用,实现了从原有的 40 多套 Oracle 数据库向仅 9 套 TDengine集群的精简替换。在迁移过程中ÿ…...

【问题解决】本机navicat连接云服务器mysql
一般情况下,当你使用navicat等工具连接云服务器会因为mysql的安全机制,导致无法连接root用户,但是在测试环境中,不考虑安全性的前提条件下,可以通过修改MySQL的配置文件来连接云服务器mysql的root用户。 选择数据库&am…...

STM32F407 的通用定时器与串口配置深度解析
在 STM32F407 芯片的开发过程中,通用定时器和串口的配置与使用是极为关键的技能点。本文将结合提供的代码示例,深入剖析这两个模块的配置流程、工作原理以及实际应用,助力开发者更好地掌握相关技术。 一、通用定时器 (一&#x…...

深入探究Linux项目自动化构建工具:make与Makefile
目录 引言 一、make与Makefile概述 1.1 背景 1.2 理解 二、make工作原理 2.1 查找Makefile 2.2 确定目标文件 2.3 处理文件依赖 三、Makefile实例分析 3.1 简单C程序示例 3.2 项目清理机制 四、结合行缓冲区概念的有趣现象 五、结语 引言 在Linux软件开发的世界里…...

【Hive入门】Hive基础操作与SQL语法:DDL操作全面指南
目录 1 Hive DDL操作概述 2 数据库操作全流程 2.1 创建数据库 2.2 查看数据库 2.3 使用数据库 2.4 修改数据库 2.5 删除数据库 3 表操作全流程 3.1 创建表 3.2 查看表信息 3.3 修改表 3.4 删除表 4 分区与分桶操作 4.1 分区操作流程 4.2 分桶操作 5 最佳实践与…...

STM32F103 “BluePill” 上的 DMA 原理与实践
摘要:本文深入浅出地介绍什么是 DMA(直接存储器访问),它的核心原理、硬件架构,以及在 STM32F103(BluePill)上常见的几种使用场景(ADC、UART、内存拷贝等)。通过对比 CPU 轮询、中断、DMA 三种方式的数据搬运效率,结合寄存器级和 HAL 库示例代码,并附带性能测试与优化…...

软考软件设计师30天备考指南
文章目录 一、考情分析(一)综合知识(二)案例分析 二、30天学习规划(一)第1 - 5天:基础夯实(二)第6 - 10天:核心知识突破(三)第11 - 15…...

比较:AWS VPC peering与 AWS Transit Gateway
简述: VPC 对等连接和 Transit Gateway 用于连接多个 VPC。VPC 对等连接提供全网状架构,而 Transit Gateway 提供中心辐射型架构。Transit Gateway 提供大规模 VPC 连接,并简化了 VPC 间通信管理,相比 VPC 对等连接,支持大量 VPC 的 VPC 间通信管理。 VPC 对等连接 AWS V…...

【AI大模型】MCP:AI应用的“超级扩展坞”
一、什么是MCP MCP(Model Context Protocol,模型上下文协议)是一种新兴的开放协议,于2024年11月由Anthropic公司(Claude的开发者)开源。它的核心目标是建立一个类似USB-C的标准化协议,统一AI模…...

线程封装
目录 makefile Thread.hpp main.cc 以面向对象的方式造轮子 #ifndef _THREAD_HPP__ // 如果没有定义过 _THREAD_HPP__ #define _THREAD_HPP__ // 则定义 _THREAD_HPP__// 这里是头文件的实际内容(类、函数声明等)#endif // 结束条件…...

【Java后端】MyBatis 与 MyBatis-Plus 如何防止 SQL 注入?从原理到实战
在日常开发中,SQL 注入是一种常见但危害巨大的安全漏洞。如果你正在使用 MyBatis 或 MyBatis-Plus 进行数据库操作,这篇文章将带你系统了解:这两个框架是如何防止 SQL 注入的,我们又该如何写出安全的代码。 什么是 SQL 注入&#…...

智能穿戴的终极形态会是AR眼镜吗?
清晨的地铁里,戴着普通眼镜的小张正通过镜片查看实时导航路线,眼前的虚拟箭头精准指引换乘方向;手术室里,主刀医生透过镜片看到患者血管的3D投影,如同获得透视眼般精准避开危险区域;装修现场,设…...
Hive3.1.2安装指南)
ubantu18.04(Hadoop3.1.3)Hive3.1.2安装指南
说明:本文图片较多,耐心等待加载。(建议用电脑) 注意所有打开的文件都要记得保存。本文的操作均在Master主机下进行 第一步:准备工作 本文是在之前Hadoop搭建完集群环境后继续进行的,因此需要读者完成我之…...

Hive 多表查询案例
文章目录 前提条件Hive 多表查询案例JOIN案例JOIN查询数据准备1. 内连接(INNER JOIN)2. 左外连接(LEFT OUTER JOIN)3. 右外连接(RIGHT OUTER JOIN)4. 全外连接(FULL OUTER JOIN)5. 多…...
)
4.23刷题记录(栈与队列专题)
第一部分:基础知识 栈先进后出,队列先进先出栈用stack实现,主要函数有pop,push,top队列由queue或者deque实现,主要函数有front,back,push,pop,emplace&#…...
)
Python常用的第三方模块之【jieba库】支持三种分词模式:精确模式、全模式和搜索引擎模式(提高召回率)
Jieba 是一个流行的中文分词Python库,它提供了三种分词模式:精确模式、全模式和搜索引擎模式。精确模式尝试将句子最精确地切分,适合文本分析;全模式则扫描文本中所有可能的词语,速度快但存在冗余;搜索引擎…...

Redisson实战:分布式系统中的五大典型应用场景
引言 在分布式系统架构中,数据一致性、高并发控制和资源协调是开发者面临的核心挑战。Redisson作为基于Redis的Java客户端,不仅提供了丰富的分布式对象和服务,还简化了分布式场景下的编程模型。本文将通过实际代码示例,解析Redis…...

webrtc建立连接的过程
WebRTC 连接全过程:从零到视频通话的每一步 WebRTC 是个神奇的技术,让浏览器直接进行点对点(P2P)音视频通话或数据传输,不用每次都靠服务器中转。想知道 Alice 和 Bob 是怎么通过 WebRTC 建立视频通话的吗?…...

system verilog 语句 耗时规则
在 SystemVerilog 中,确实有一类语句是**不消耗仿真时间(zero simulation time)**的,我们一般叫它们: ✅ 零延迟语句(Zero-Time Statements) 🔹1. 什么是“不费时间”的语句? 这些语句在仿真时…...

【Docker】在Ubuntu平台上的安装部署
写在前面 docker作为一种部署项目的辅助工具,真是太好用了需要魔法,不然无法正常运行笔者环境:ubuntu22.04 具体步骤 更新系统包索引 sudo apt update安装必要依赖包 sudo apt install -y apt-transport-https ca-certificates curl softwa…...

2025年阅读论文的常用工具推荐
在快速发展的学术界,阅读和整理论文的能力对于研究者和学生来说至关重要。随着科技的进步,各种工具应运而生,帮助我们更高效地处理文献。本文将为您推荐一些2025年最常用的阅读论文工具,让您的学术之路更加顺畅。 1. SumiNote S…...

pod内部共享命名空间与k8s命名空间是一个东西吗?
文章目录 小知识-命名空间**下面着重介绍一下刚刚提到的内部命名空间**IPC NamespaceNetwork Namespace 本文摘自于我的免费专栏《Kubernetes从0到1(持续更新)》请多关注 小知识-命名空间 注意,首先我要强调一点,Kubernetes命名空…...

Linux笔记---进程间通信:匿名管道
1. 管道通信 1.1 管道的概念与分类 管道(Pipe) 是进程间通信(IPC)的一种基础机制,主要用于在具有亲缘关系的进程(如父子进程、兄弟进程)之间传递数据,其核心特性是通过内核缓冲区实…...
桥接模式)
JAVA设计模式——(三)桥接模式
JAVA设计模式——(三)桥接模式(Bridge Pattern) 介绍理解实现武器抽象类武器实现类涂装颜色的行为接口具体颜色的行为实现让行为影响武器修改武器抽象类修改实现类 测试 适用性 介绍 将抽象和实现解耦,使两者可以独立…...

设计模式--工厂模式详解
工厂模式 作用: 实现了创建者与调用者的分离 详细分类 简单工厂模式 工厂方法模式 抽象工厂模式 OOP七大原则: 开闭原则:一个软件的实体应该对拓展开发,对修改关闭 依赖反转原则:要针对接口编程,不…...

每天五分钟深度学习PyTorch:图像的处理的上采样和下采样
本文重点 在pytorch中封装了上采样和下采样的方法,我们可以使用封装好的方法可以很方便的完成采样任务,采样分为上采样和下采样。 上采样和下采样 下采样(缩小图像)的主要目的有两个:1、使得图像符合显示区域的大小;2、生成对应图像的缩略图。 下采样( 放大图像)的…...

前端面试场景题
目录 1.项目第一次加载太慢优化 / vue 首屏加载过慢如何优化 2.说说了解的es6-es10的东西有哪些 ES6(ES2015)之后,JavaScript 新增了许多实用的数组和对象方法,下面为你详细介绍: 3.常见前端安全性问题 XSS&#…...

国际化不生效
经过我的重重检查 最终发现是 版本问题。 原本下载默认next版本cnpm install vue-i18nnext 下载 国际化插件 cnpm install vue-i18n^9.14.3 删除掉node_models,再重新加载包:cnpm install 这时候就可以正常显示了 国际化操作: en.js zh…...

新一代人工智能驱动医疗数智化:范式变革、实践方向及路径选择
人工智能(AI)正以前所未有的速度重构医疗健康行业的底层逻辑,从数据获取、知识建模到临床决策支持,AI不仅是“辅助工具”,更日益成为医疗生产力体系的核心引擎。随着大模型、计算平台和数智基础设施的迅猛发展,医疗数智化正进入从“点状创新”走向“系统重构”的深水区。…...
颜色空间转换-----将图像从 RGB 色彩空间转换为 I420 格式函数RGB2I420())
OpenCV 图形API(55)颜色空间转换-----将图像从 RGB 色彩空间转换为 I420 格式函数RGB2I420()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 将图像从 RGB 色彩空间转换为 I420 色彩空间。 该函数将输入图像从 RGB 色彩空间转换为 I420。R、G 和 B 通道值的常规范围是 0 到 255。 输出图…...

大模型安全吗?数据泄露与AI伦理的黑暗面!
大模型安全吗?数据泄露与AI伦理的黑暗面! 随着人工智能技术的飞速发展,尤其是大型语言模型(如GPT-3、BERT等)的出现,AI的应用场景越来越广泛,从智能客服到内容生成,从医疗诊断到金融…...

穿越链路的旅程:深入理解计算机网络中的数据链路层
一、引言 在计算机网络的七层模型中,数据链路层(Data Link Layer) 是连接物理世界与逻辑网络世界的关键一环。它位于物理层之上,网络层之下,负责将物理层的“比特流”转换成具有结构的数据帧,并确保数据在…...

《AI大模型应知应会100篇》第35篇:Prompt链式调用:解决复杂问题的策略
第35篇:Prompt链式调用:解决复杂问题的策略 摘要 在大模型应用中,单次提示的能力往往受限于上下文长度和任务复杂度。为了解决这些问题,Prompt链式调用应运而生。本文将深入探讨如何通过分解任务、设计逻辑链路、传递中间结果&am…...

管理100个小程序-很难吗
20公里的徒步-真难 群里的伙伴发起了一场天目山20公里徒步的活动,想着14公里都轻松拿捏了,思考了30秒后,就借着春风带着老婆孩子就出发了。一开始溪流清澈见底,小桥流水没有人家;青山郁郁葱葱,枯藤老树没有…...

算法恢复训练-Part01-数组
注:参考的某算法训练营的计划 核心注意点 在 Golang(和大多数主流语言,如 C/C)中,二维数组按行访问的效率更高。因为它符合 Go 的内存连续存储结构,能提高 CPU Cache 命中率,减少内存跳跃带来…...

软件黑盒与白盒测试详解
黑盒测试与白盒测试的核心对比 一、定义与核心目标 黑盒测试 定义:将程序视为“黑盒”,仅通过输入和输出验证功能是否符合需求规格,不关注内部代码逻辑。目标:确保功能完整性、输入输出正确性及用户体验,例如验证购物车…...

本文通俗简介-优雅草星云物联网AI智控系统软件介绍-星云智控是做什么用途的??-优雅草卓伊凡
本文通俗简介-优雅草星云物联网AI智控系统软件介绍-星云智控是做什么用途的??-优雅草卓伊凡 星云智控:物联网设备实时监控的革新力量 一、引言 在科技飞速发展的当下,物联网技术的广泛应用使得各类设备的实时监控与管理变得愈发…...

达梦统计信息收集情况检查
查询达梦某个对象上是否有统计信息 select id,T_TOTAL,N_SMAPLE,N_DISTINCT,N_NULL,BLEVEL,N_LEAF_PAGES,N_LEAF_USED_PAGES,LAST_GATHERED from sysstats where id IN (select id from sysobjects where upper(name)upper(&objname));可能有系统对象,可以增加…...

【MQ篇】RabbitMQ之发布订阅模式!
目录 引言一、 回顾:简单模式与工作队列模式的局限 😔二、 发布/订阅模式详解:消息的“广播站” 📻三、 RabbitMQ 中的交换机类型:不同的“广播方式” 📻四、 Java (Spring Boot) 代码实战Fanout 模式的完整…...
