Sklearn 与 TensorFlow 机器学习实用指南-第八章 降维-笔记

补充：

本文是关于《Sklearn 与 TensorFlow 机器学习实用指南》的学习笔记，基于八、降维 - 【布客】Sklearn 与 TensorFlow 机器学习实用指南 第二版，感谢译者

本文和原文的区别：

本文会更精简、系统地表述书中概念，会对书中未介绍的陌生概念加以解释，每行我都会添加注释，介绍具体做了什么。

后续会持续更新所有章节

正文开始 ~
————————————————

当数据集的维度过高时，模型训练难度增大、过拟合风险上升且计算资源消耗剧增。这种现象通常被称为维数灾难（curse of dimentionality）。

应对策略：
降维：降低特征维度，减少特征数量，简化问题。

选择重要的维度，丢弃不太重要的：

例如，对于 MNIST 图片集，由于图片四周边缘部分的像素几乎总是白的，完全可以将这些像素从你的训练集中扔掉而不会丢失太多信息。

利用相邻像素的高度相关性，整合不同的维度：由于相邻像素的高度相关性，整合维度可以在不丢失太多信息的情况下有效地降低数据维度。

例如：
1. 空间金字塔
概念：将图像划分为不同尺度的子区域（如不同大小的块），并为每个子区域提取特征。
特点：
利用相邻像素的空间相关性，从多个尺度上捕捉图像信息。
减少维度的同时保留多尺度特征。

2. 局部特征提取
概念：通过滑动窗口或其他方法在图像中提取局部特征（如SIFT、HOG）。
特点：
捕捉相邻像素的局部信息，同时减少全局维度。
可以通过降维技术（如PCA）进一步压缩特征向量。
 

3. 亚像素卷积
概念：将多个低分辨率图像的特征组合起来，恢复高分辨率的输出。
特点：
利用相邻像素的信息来提高分辨率，同时减少计算复杂度。
常用于超分辨率重建等任务。

4. 特征金字塔网络（FPN）
概念：通过不同层次的卷积操作提取多尺度特征图。
特点：
利用低层特征图中的细节信息和高层特征图中的语义信息，构建多层次的特征表示。
有效降低维度的同时保留丰富的图像内容。

5.平均池化（Average Pooling）
概念：将相邻像素进行平均或求和操作，得到低分辨率的特征图。
特点：
简单有效地降维，同时保留局部信息。
常用于减少计算量和参数数量。

6. 图像压缩与量化
概念：将相邻像素合并或进行某种形式的量化编码。
特点：
减少存储空间和传输带宽的需求。
可应用于实时视频处理和流媒体等场景。

降维的特点：
1. 在降维过程中可能会丢失某些信息，应该先尝试使用原始的数据来训练，如果训练速度太慢的话再考虑使用降维
2. 通过降维去除噪声或冗余特征（这种情况通常不会发生，它只会加快你训练的速度）
3. 降维将高维数据映射到二维或三维空间，便于直观展示和理解，便于可视化（Visualization）


在这一章里，会介绍：
两种主要的降维方法：投影（projection）和流形学习（Manifold Learning），
三种流行的降维技术：主成分分析（PCA），核主成分分析（Kernel PCA）和局部线性嵌入（LLE）。

1. 维度灾难

在低维空间中，大量数据点可能会集中在某些区域（如中心区域），在高维空间中，数据更倾向于分布在边界处（一个简单的理解思路参考https://www.kpfans.com/article/LmWKKJXWB3.html），且随机选取的点之间距离变得更大，主要是维度增加导致的数据稀疏性和欧氏距离的平方和累积效应（在高维空间中，即使每个坐标轴上的变化相对较小，由于平方和的积累效应，最终导致欧几里得距离显著增大）共同作用的结果。

维度过高的影响：
1. 距离度量失真：高维空间中点之间的相对距离变得不明显，难以区分。
2. 过拟合问题加剧：高维空间下，新增的新实例可能远离任何训练实例，这使得预测的可靠性远低于较低维度数据，模型可能过度适应训练数据，导致泛化能力下降，增加过拟合风险。

3. 计算复杂度上升：处理大量特征会显著增加计算时间和资源消耗。

补充：
理论上来说，维数爆炸的一个解决方案是增加训练集的大小从而达到拥有足够密度的训练集。不幸的是，在实践中，达到给定密度所需的训练实例的数量随着维度的数量呈指数增长。如果只有 100 个特征并且假设它们均匀分布在所有维度上，那么如果想要各个临近的训练实例之间的距离在 0.1 以内，需要比宇宙中的原子还要多的训练实例。

2. 降维的主要方法：投影与流形学习

这两种主要方法适用的情况：训练实例并不是在所有维度上均匀分布的。许多特征几乎是常数，而其他特征则高度相关。结果，所有训练实例实际上位于（或接近）高维空间的低维子空间内。

例如：左图，所有训练实例的分布都贴近一个平面：这是高维（3D）空间的较低维（2D）子空间。将每个训练实例垂直投影到这个子空间上，就可以得到的新 2D 数据集。如右图

 

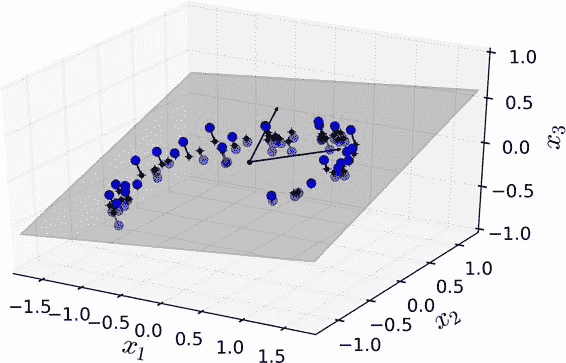
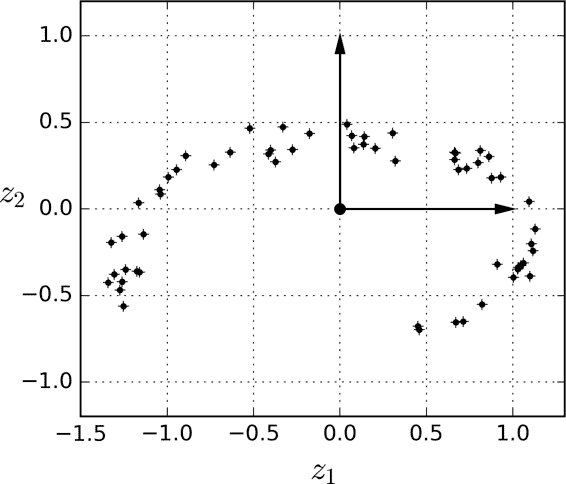
上述方法就是投影，但投影并不总是降维的最佳方法。在很多情况下，子空间可能会扭曲和转动，例如瑞士滚动玩具数据集

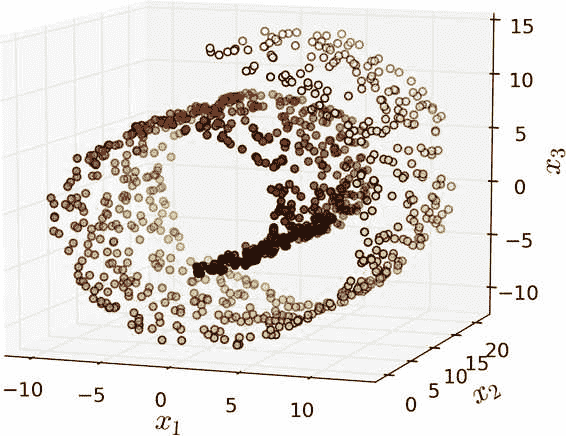
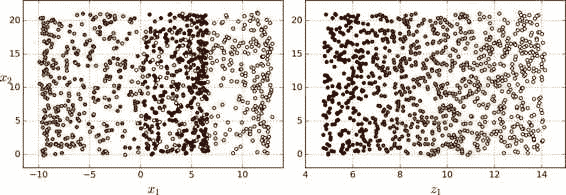
简单地将数据集投射到一个平面上（例如，直接丢弃x3方向）会将瑞士卷的不同层叠在一起，如左图 。但是，真正想要的类似右图的 2D 数据集。

2.1 投影（Projection）

定义：通过线性变换，将高维数据映射到低维空间的降维方法
常见的投影方法包括主成分分析（PCA）、线性判别分析（LDA）等。

2.2 流形学习（Manifold Learning）

定义：流形学习是一种非线性的降维技术，旨在捕捉数据在高维空间中的内在流形结构。
常见的流形学习方法包括局部线性嵌入（LLE）、等距映射（Isomap）、拉普拉斯特征映射（Laplacian Eigenmap）等。

补充：

流形：是一个拓扑空间，它在每一点周围都有一个邻域，这个邻域与欧几里得空间（如平面或三维空间）在拓扑结构上相同。这种局部性质使得流形可以被“展开”或“映射”到欧几里得空间中进行分析。
例如：二维流形：最简单的例子是球面，它是一个二维流形，因为在每个点周围都可以找到一个与平面相同的邻域。

流形结构：流形结构指的是附加在流形上的额外数学属性或组织方式。这些结构可以赋予流形特定的行为或性质，使其适用于不同的应用场景。
例如：微分结构（Differentiable Structure）：允许在流形上定义导数和积分等微积分运算，使得流形成为微分 manifold。

流形空间：指由一个或多个流形及其结构所构成的整体空间。它可以是一个单一的流形，也可以是多个流形通过某种方式组合而成的空间。

流形猜想（Manifold Hypothesis）：机器学习中的一个重要假设，认为高维数据往往分布在某个低维的流形上。

以瑞士卷为例
例如，在第一行中，瑞士卷在三维空间中（图左上），分类边界会相当复杂，但在二维展开的流形空间中（图右上），分类边界是一条简单的直线，被分为两类。

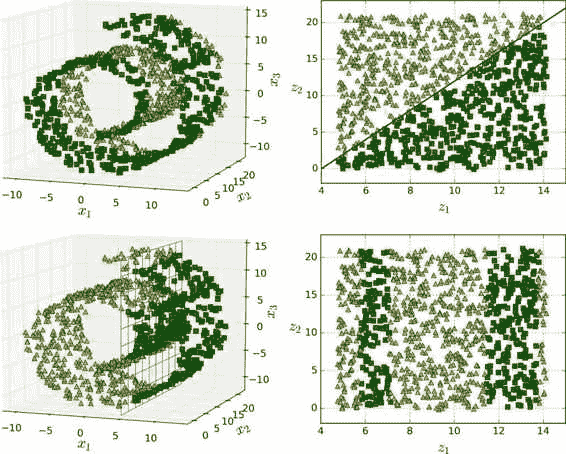
但是，这个假设并不总是成立。例如，在图最下面一行，决策边界位于x1 = 5（图左下）。这个决策边界在原始三维空间（一个垂直平面）看起来非常简单，但在展开的流形中却变得更复杂了（四个独立线段的集合）（图右下）。

总结：
降维→训练速度会加快
降维≠更好的训练效果，效果取决于数据集

投影和流形学习的区别：
线性 vs 非线性：投影通常是线性的，而流形学习是非线性的。
全局 vs 局部特性：投影方法通常关注数据的整体结构（全局特性），而流形学习则关注数据的局部几何结构。

3. 主成分分析

定义：找到接近数据集分布的超平面，然后将所有的数据都投影到这个超平面上。

3.1 保留最大的方差

例如：图左侧是二维数据集，以及三个不同的轴。图右边是将数据集投影到每个轴上的结果。

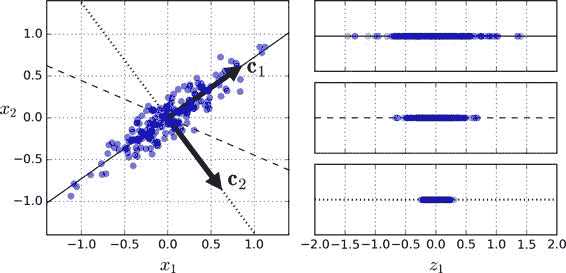
原理：

对轴来说，由于高方差表示该方向上的数据变化较大，包含了更多关于数据分布的信息，因此通过优先选择高方差的方向进行投影，可以最大程度地保留原始数据中的信息，减少降维带来的信息损失。
上图中的轴的方差：实线轴的方差＞虚线轴的方差＞点线轴的方差

另一个角度来看，选择使得将原始数据集投影到该轴上的均方距离最小的轴。
均方距离（Mean Squared Distance, MSD）：数据点在投影后与原始位置之间的平均平方距离。均方距离最小，意味着原始位置和投影后的位置差距越小，就更多的保留了原始数据中的信息

 

3.2 主成分（Principle Componets）

PCA选择的主成分轴的原则：第一个主成分具有最大的方差，后续的主成分与之前的主成分正交，并且在剩余空间中方差最大，依次类推。

定义：第i个轴的单位向量被称为第i个主成分（PC）

例如：在上面的图中，第一个 PC 是实线轴的单位向量c1，第二个 PC 是点线轴的单位向量c2。

主成分的方向不稳定：如果打乱训练集并再次运行 PCA，则某些新 PC 可能会指向与原始 PC 方向相反。但是，它们通常仍位于同一轴线上。在某些情况下，一对 PC 甚至可能会旋转或交换，但它们定义的平面通常保持不变。

如何找到训练集的主成分？
奇异值分解（SVD）的标准矩阵分解技术，可以将训练集矩阵X分解为三个矩阵U·Σ·V^T的点积，其中V^T包含我们想要的所有主成分

import numpy as np
X_centered = X - X.mean(axis=0)  # 中心化处理
U, s, V= np.linalg.svd(X_centered)  # 奇异值分解
c1 = V.T[:, 0]  # 第一个主成分
c2 = V.T[:, 1]  # 第二个

3.3 投影到d维空间

定义：确定了所有的主成分，就可以通过将数据集投影到由前d个主成分构成的超平面上，从而将数据集的维数降至d维。
如何投影：计算训练集矩阵X和Wd的点积

W2 = V.T[:, :2]  # Wd，V^T的前d列组成的矩阵，此时d=2，代表前两个主成分矩阵
X2D = X_centered.dot(W2)  # 将训练集投影到由前两个主成分定义的超平面上

3.4 使用 Scikit-Learn

from sklearn.decomposition import PCApca = PCA(n_components=2)  # n_components：将数据集的维度降至两维
X2D = pca.fit_transform(X)  # 降维数据，pca会自动处理数据的中心化
pca.components_.T[:, 0]  # 获得第一个主成分

3.5 方差解释率（Explained Variance Ratio）

定义：方差解释率表示位于每个主成分轴上的数据集方差的比例，反映了模型预测值与实际值之间的拟合程度。高值意味着模型对数据变化的解释能力较强。

值范围：在0到1之间。
1：模型完美解释数据变化
0：模型无法解释数据变化

print(pca.explained_variance_ratio_)
# [0.84248607  0.14631839]  84.2% 的数据集方差位于第一轴，14.6% 的方差位于第二轴

3.6 选择正确的维度

通常我们倾向于选择加起来到方差解释率能够达到足够占比（例如 95%）的维度的数量，而不是任意选择要降低到的维度数量。

pca = PCA()  # 不指定维度
pac.fit(X)  # 在不降维的情况下进行 PCA
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95)+1  # 计算出保留训练集方差 95% 所需的最小维数# 还有一种方法
pca = PCA(n_components=0.95)  # n_components设置为 0.0 到 1.0 之间的浮点数，表明希望保留的方差解释率
X_reduced = pca.fit_transform(X)

画出方差解释率关于维数的函数

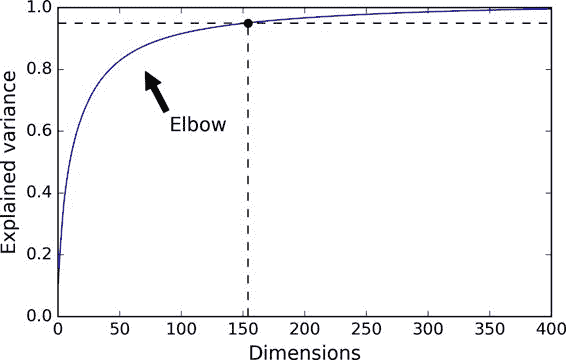
参见图，曲线中通常会有一个肘部，方差解释率停止快速增长。可以将其视为数据集的真正的维度

3.7 PCA 压缩

通过应用 PCA 投影的逆变换，可以降维后的数据集解压缩回原维度，这并不会还原成最原始的数据，因为投影丢失了一些信息（在 5% 的方差内），但它可能非常接近原始数据
重构误差（reconstruction error）：原始数据和重构数据之间的均方距离（压缩然后解压缩）

pca = PCA(n_components=154)  # n_components：将数据集的维度降至 154 维
X_mnist_reduced = pca.fit_transform(X_mnist)  # 将MNIST 数据压缩到154维
X_mnist_recovered = pca.inverse_transform(X_mnist_reduced)  # 解压缩回 784 维

前后图像的对比

逆变换的公式

3.8 增量 PCA（Incremental PCA）

先前 PCA 需要在内存中处理整个训练集，以便奇异值分解算法的运行

增量 PCA（IPCA）算法：将训练集分批，并一次只对一个批量使用 IPCA 算法
增量式PCA的优势：
适合大数据集：不需要一次性加载所有数据到内存
可以在线处理：逐批读取和更新模型参数
节省内存：特别适用于内存有限的环境
通过多次迭代更新主成分估计器，最终得到训练好的PCA模型

from sklearn.decomposition import IncrementalPCA  # 增量 PCAn_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_mnist, n_batches):  # 分成 100 个小批量inc_pca.partial_fit(X_batch)   # 对每一个最小批量使用 IPCA 算法
X_mnist_reduced = inc_pca.transform(X_mnist)  # 降维数据# 加载大文件数据时，可以用 np.memmap 将磁盘上的文件映射到内存，形成一个可以像数组一样访问的对象
X_mm = np.memmap(filename,  dtype='float32',  # filename：要打开的文件名mode='readonly',  # mode=readonly：以只读模式打开文件shape=(m, n))  # shape=(m, n)：指定数组的形状，即有m行n列的数据
batch_size = m//n_batches
inc_pca = IncrementalPCA(n_components=154,   # n_components=154：指定要保留的主成分数量，即降维后的维度数batch_size=batch_size)  # batch_size=batch_size：每一批处理的数据量
inc_pca.fit(X_mm)  # 用于训练模型，接受数据输入，并计算主成分

3.9 随机 PCA（Randomized PCA）

定义：利用随机投影的思想，生成随机矩阵并与原始数据相乘，将高维数据映射到低维空间，基于随机矩阵理论，确保即使在降低维度后，主要的数据特征仍得以保留

优点：

引入随机性以减少计算复杂度，并能保持数据重要特征，特别适用于处理大数据集。计算复杂度是O(m × d^2) + O(d^3)，而不是O(m × n^2) + O(n^3)
缺点：

由于使用了随机投影，结果可能会有一定的随机性，建议多次运行并取平均值以提高稳定性。需要确保数据在预处理阶段具有良好的分布特性，才能更好地捕捉主要特征

rnd_pca = PCA(n_components=154, svd_solver='randomized')  # 随机 PCA
X_reduced = rnd_pca.fit_transform(X_mnist)  # 降维数据

4.核 PCA（Kernel PCA）

在第5章中，我们讨论了核技巧，一种将实例隐式映射到非常高维空间（称为特征空间）的数学技术，让支持向量机可以应用于非线性分类和回归

核 PCA（kPCA）：执行复杂的非线性投影来降低维度
优点：通常能够很好地保留投影后的簇，有时甚至可以展开分布近似于扭曲流形的数据集

具体步骤：
1. 数据预处理
标准化或归一化：确保各个特征具有相似的尺度，避免数值较大的特征主导分析
2. 核函数的选择
根据数据特性选择合适的核函数，常见的核函数包括：线性核、多项式核、径向基函数（RBF）核、sigmoid核，通过它将原始的低维数据点映射到一个高维甚至无穷维的空间中
（这个过程是隐式的，也就是说，我们不需要显式地计算出每个数据点在高维空间中的坐标，而是通过核矩阵来间接地表示这些信息）
3. 构建核矩阵
计算每个样本对之间的核函数值，形成一个n×n的核矩阵H。其中，H_ij = K(x_i, x_j)。这个矩阵包含了所有样本对之间的相似性度量
4. 在高维空间中进行PCA，中心化核矩阵
具体来说，我们需要计算高维空间中的协方差矩阵，并找到其中最大的特征值和对应的特征向量（主成分）。这些主成分对应的就是在原始输入空间中最能解释数据变化的方向
然而，直接计算高维空间的协方差矩阵是不现实的，因为维度可能非常高甚至无穷大，幸运的是，我们可以通过核矩阵H来间接地完成这个过程，我们可以利用核矩阵的迹和特征值分解来进行PCA分析
对核矩阵进行中心化处理，减去均值向量，得到中心化的核矩阵：H_centered = H - (1/n) * trace(H) * eye(n)
5. 特征值分解
# 对中心化的核矩阵进行特征值分解，计算其特征值和特征向量。特征值表示数据在对应方向上的方差，特征向量则是主成分的方向

 6. 选择主成分
根据特征值的大小顺序，保留前k个特征向量作为主要的主成分，忽略其余较小的特征值
7. 将主成分映射回原始空间
利用核矩阵和所选的主成分，用这些特征向量对原始数据进行线性组合，从而得到在输入空间中的低维表示
8. 应用与分析

 进行后续的数据分析、降维或可视化

from sklearn.decomposition import KernelPCArbf_pca = KernelPCA(n_components=2,  # 降维后的维度kernel='rbf',   # rbf核gamma=0.04  # rbf核函数中的参数)
X_reduced = rbf_pca.fit_transform(X)  # 降维数据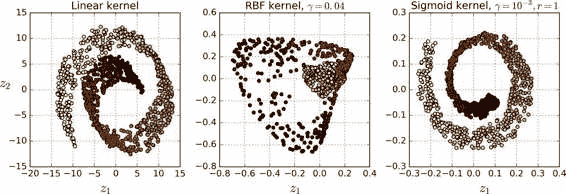

4.1 选择一种核并调整超参数

由于 kPCA 是无监督学习算法，因此没有明显的性能指标来确定最佳的核方法和超参数值。但是，降维通常是监督学习任务（例如分类）的准备步骤，因此可以使用网格搜索来选择让任务达到最佳表现的核方法和超参数

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipelineclf = Pipeline([("kpca", KernelPCA(n_components=2)),  # 执行核pca，将维度降至两维("log_reg", LogisticRegression())  # Logistic 回归分类
])
param_grid = [{"kpca__gamma": np.linspace(0.03, 0.05, 10),"kpca__kernel": ["rbf", "sigmoid"]}]
grid_search = GridSearchCV(clf, param_grid, cv=3)  # Grid SearchCV为 kPCA 找到最佳的核和gamma值
grid_search.fit(X, y)  # 拟合数据

另一种完全为非监督的方法，是选择产生最低重建误差的核和超参数，但是，由于核技巧，重建并不像线性 PCA 那样容易。
下图显示了原始瑞士卷3D数据集（左上角），并且使用RBF核应用kPCA后生成的二维数据集（右上角）。
由于核技巧，这在数学上等同于使用特征映射φ将训练集映射到无限维特征空间（右下），然后使用线性PCA将变换的训练集投影到 2D。

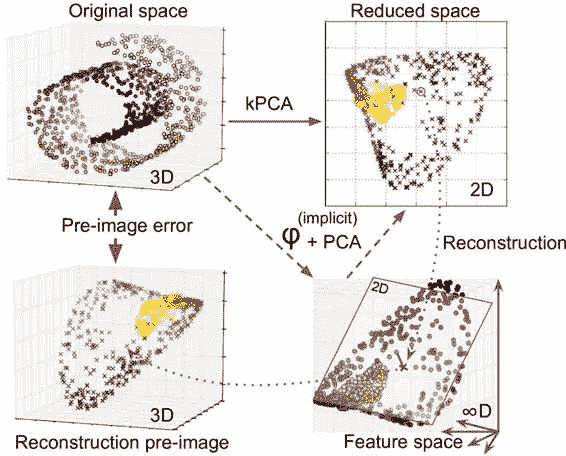
如果我们可以在缩减空间中对给定实例实现反向线性PCA步骤，则重构点将位于特征空间中，而不是位于原始空间中。但由于特征空间是无限维的，我们不能找出重建点，因此我们无法计算真实的重建误差。
幸运的是，可以在原始空间中找到一个贴近重建点的点。这被称为重建前图像（reconstruction pre-image），然后就可以测量其与原始实例的平方距离。然后，选择最小化重建前图像错误的核和超参数。

# 解决方案一：
# 训练一个监督回归模型
rbf_pca = KernelPCA(n_components=2,kernel="rbf",gamma=0.0433,fit_inverse_transform=True  # 将预计实例作为训练集，并将原始实例作为训练目标。KernelPCA仅仅当 fit_inverse_transform = True 的情况下才会创建inverse_tranfrom()方法)
X_reduced = rbf_pca.fit_transform(X)  # 降维数据
X_preimage = rbf_pca.inverse_transform(X_reduced)  # 重建数据# 计算误差
from sklearn.metrics import mean_squared_error
mean_squared_error(X, X_preimage)   # mse误差：32.786308795766132
# 然后使用交叉验证的方格搜索来寻找最小化重建前图像误差的核方法和超参数。

4.2 LLE（LocallyLinearEmbedding）

定义：非线性降维（NLDR）方法，而且是一种流形学习技术。LLE 首先测量每个训练实例与其最近邻（c.n.）之间的线性关系，然后寻找能最好地保留这些局部关系的训练集的低维表示（稍后会详细介绍） 
优点：特别擅长展开扭曲的流形，尤其是在没有太多噪音的情况下

from sklearn.manifold import LocallyLinearEmbeddinglle = LocallyLinearEmbedding(n_components=2,  # 降维后的维度n_neighbors=10  # 最近邻个数)
X_reduced = lle.fit_transform(X)  # 降维数据

如图，瑞士卷被完全展开，实例之间的距离保存得很好。但是，距离不能在较大范围内保留的很好：展开的瑞士卷的左侧被挤压，而右侧的部分被拉长。尽管如此，LLE 在对流形建模方面做得非常好。

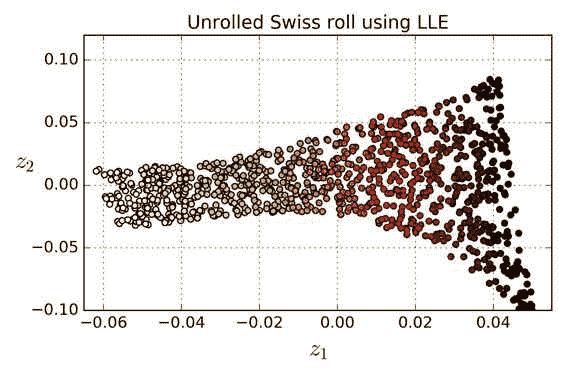
工作原理：
1. 寻找最近邻： 对于每个数据点 x_i，找到其在高维空间中的 k 个最近邻居。这通常使用k近邻算法实现。
2. 计算局部重建权重：找到权重w[i, j]从而使x_i和Σ w[i, j] x_j, j = 1 -> m之间的平方距离尽可能的小
3. 构建权重矩阵：将所有点的权重组合成一个权重矩阵 W，其中非邻居对应的权重为零。
4. 降维过程：将高维数据 X 映射到低维空间，得到新的表示Z，使得每个z_i 满足类似的线性关系。z_i和Σ w_hat[i, j] z_j, j = 1 -> m之间的平方距离尽可能的小，注意，此时是保持权重不变，并在低维空间中找到实例图像的最佳位置
5. 求解低维映射：通过最小化上述误差函数，找到最优的低维表示Z，这通常涉及到矩阵分解或优化算法，如拉格朗日乘数法。
6. 结果输出：将高维数据点X映射到低维空间后的坐标矩阵Z，即为降维后的表示。

时间复杂度：查找k个最近邻为O(m log(m) n log(k))，优化权重为O(m n k^3)，建立低维表示为O(d m^2)。不幸的是，最后一项m^2使得这个算法在处理大数据集的时候表现较差。

5. 其他降维方法

还有很多其他的降维方法，Scikit-Learn 支持其中的好几种。这里是其中最流行的：

5.1多维缩放（Multi-Dimensional Scaling, MDS）

定义：其核心思想是通过优化过程找到一个低维表示，使得样本之间的距离在低维和高维空间中尽可能相似。
基本步骤：
1. 计算距离矩阵：首先，在高维空间中计算所有样本对之间的距离，形成一个距离矩阵。
2. 求解低维配置：通过优化算法（如经典度量 MDS 使用加权最小二乘法），找到一组低维点，使得这些点之间的距离尽可能接近原始的高维距离矩阵。
3. 调整和改进：根据需要对结果进行调整，例如使用非线性方法或结合其他约束条件以提高表示的质量。
优点：
- 能够有效保持数据的整体结构和全局关系。
- 易于解释和可视化。
缺点：
- 在处理高维数据时可能计算复杂度较高。
- 对噪声数据较为敏感，可能导致降维后的结果不准确。

5.2 Isomap

定义：流形学习思想的降维技术，它通过构建最近邻图来捕捉数据的局部几何结构，并利用这些信息进行全局降维。特别适合处理具有非线性分布的数据集。

基本步骤：
1. 构建最近邻图：为每个样本找到其预定义数量的最近邻居，并建立一个邻接图。
2. 计算最短路*：通过广度优先搜索（BFS）或其他方法，计算图中每对节点之间的最短路径，形成一个相似性矩阵。
3. 应用主成分分析（PCA）：对相似性矩阵进行 PCA 分析，得到低维表示。
优点：
能够有效地处理非线性数据分布。
具有良好的流形学习能力，能够捕捉到数据的潜在结构。
缺点：
计算复杂度较高，尤其是在处理大数据时。
对参数的选择（如最近邻居的数量）敏感，可能影响结果的质量。

5.3 t-分布随机邻域嵌入（t-SNE）

定义：一种基于概率的降维技术，主要用于高维数据的可视化。它结合了随机近邻和 t-分布的思想，能够在低维空间中保持数据的局部结构。
基本步骤：
1. 计算条件概率：在高维空间中，为每个点计算其与所有其他点之间的条件概率分布（条件概率是指在给定某个条件下，另一个事件发生的概率。）。
2. 定义t-分布：在低维空间中，使用 t-分布模拟这些条件概率。
3. 优化低维表示：通过梯度下降等优化算法，最小化两个分布之间的KL散度，得到最终的低维映射。
优点：
能够有效地保留数据的局部结构和簇的特性。
特别适合用于高维数据的二维或三维投影和可视化。
缺点：
对初始参数的选择较为敏感，可能导致收敛到局部最优解。
在处理大规模数据时计算效率较低。

5.4 LDA（线性判别分析）

定义：是一种监督降维技术，旨在最大化类内一致性的同时最小化不同类别之间的距离。它通过寻找最优的投影方向，将高维数据映射到低维空间中，使得不同类别在该空间中的可分性达到最佳。

基本步骤：
1. 计算散度矩阵：包括类内散度矩阵（Sw）和类间散度矩阵（Sb）。
2. 求解广义特征值问题：找到能够最大化类别分离的投影方向，通常通过求解广义特征值问题来实现。
3. 数据投影：将高维数据投影到由这些最优投影方向张成的空间中，得到低维表示。
优点：
- 能够有效地利用类别信息进行降维。
- 适用于分类任务中的特征提取和数据预处理。
缺点：
- 受限于类别数和特征数量的关系，当类别数较多时可能会遇到维度灾难问题。
- 对小样本数据或噪声数据较为敏感。

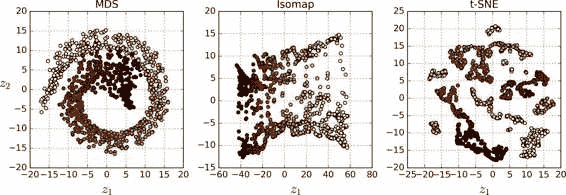
如图，使用不同的技术将瑞士卷降维至 2D