当前位置：首页 > news >正文

Floyd算法求解最短路径问题——从零开始的图论讲解(3)

news 来源：原创 2025/7/30 12:58:29

前言

Djikstra算法的缺陷

为什么无法解决负权图

模拟流程

什么是Floyd算法

Floyd算法的核心思想

状态表示

状态转移方程

边界设置

代码实现

逻辑解释

举例说明

Floyd算法的特点

结尾

前言

这是笔者图论系列的第三篇博客

第一篇:

图的概念,图的存储,图的遍历与图的拓扑排序——从零开始的图论讲解(1)_图论】图的存储与出边的排序-CSDN博客

第二篇:

Dijkstra算法求解最短路径—— 从零开始的图论讲解(2) -CSDN博客

之前的博客中呢笔者给大家介绍了图的概念,如何存图,如何简单遍历图,已经什么是图的拓扑排序

还介绍了Dijkstra算法,以及如何实现Dijkstra算法

按照之前的学习规划,本篇我们介绍另外一个求解最短路径问题的算法思想:Floyd算法

博客中出现的参考图都是笔者手画的,代码示例也是笔者手敲的!影响虽小,但请勿抄袭

Djikstra算法的缺陷

之前介绍Dijkstra 算法的时候,笔者就提到过,如果图的权值有负数,那么就无法使用Dijkstra算法去处理最短路径问题, 为什么呢?首先给大家看一个例子

请看如图,这是一个带了负权边的图:

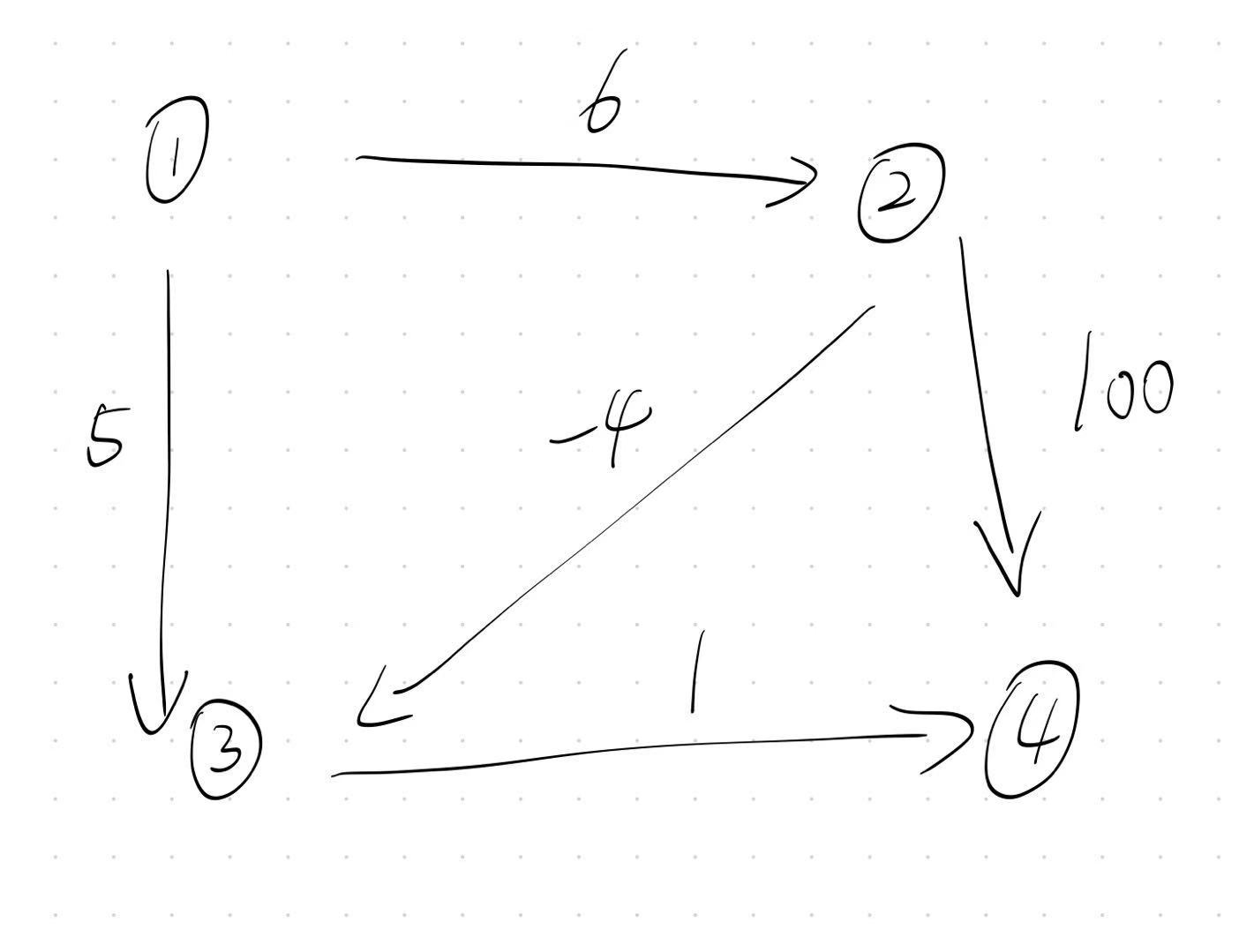
假设节点1为源点,求到达各个点的最短路径,我们使用Dijkstra 算法,结果会是怎样?请看代码

import java.util.*;public class BetterperformanceDijkstra {static   class  Node{public int v;public int w;public Node(int v, int w) {this.v = v;this.w = w;}}static  int n,m;static  List<List<Node>> list = new ArrayList<>();public static void  addEge(int u, int v, int w){list.get(u).add(new Node(v,w));}static  boolean[] vis;static int[] dist;static  final  int INF = Integer.MAX_VALUE-20000000;
public  static  void dijkstra(int start)
{Arrays.fill(dist,INF);dist[start] = 0;PriorityQueue<Node> priorityQueue = new PriorityQueue<>(((o1, o2) -> o1.w-o2.w));Node cur = new Node(start,0);priorityQueue.offer(cur);while(!priorityQueue.isEmpty()){Node temp = priorityQueue.poll();int v = temp.v;int w = temp.w;if(vis[v]){continue;//已经访问过了}vis[v] = true;if(list.get(v)==null){continue;//没有联通的点}for(Node tep : list.get(v)){int vi = tep.v;int wi = tep.w;if(dist[vi]>dist[v]+wi)//维护最短路径{dist[vi] = dist[v]+wi;priorityQueue.offer(new Node(vi,dist[vi]));}}}
}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();m = scanner.nextInt();for(int i=0;i<=n;i++){list.add(new ArrayList<>());}vis = new boolean[n+1];dist = new int[n+1];for(int i=0;i<m;i++){int a = scanner.nextInt();int b = scanner.nextInt();int c = scanner.nextInt();addEge(a,b,c);}dijkstra(1);for(int i = 1;i<=n;i++){System.out.print(dist[i]+" ");}}
}

结果如下:

可以看到,源点1到达节点4的最短路径长度为3 ,但是结果显示却是6

因此,在有些时候,使用Dijkstra 算法确实无法有效解决负权图的最短路径问题,那么这是为什么呢?

为什么无法解决负权图

首先让我们回顾一下Dijkstra算法的核心思想:

1.先选择好起点.

2.每次访问距离起点最近的,且之前没有被访问过的点

3.更新它的邻居的最短路径，并将其标记为已访问。

而Dijkstra 的算法核心原则就是

一旦某个节点 i 被选择，并且 vis[i] = true，那么我们无法通过节点 i 再次去更新到达其他点的权值了,哪怕有了更好的结果

这是一种贪心的思维策略,这个策略在所有边权都为非负数时是成立的，因为一旦确定某个节点的路径长度，后续不会出现比这个更短的路径。

但一旦图中含有负权边，这个“贪心假设”就会崩塌。
原因在于负权边会让后面的路径绕回来反而更短，但 Dijkstra 在更新某个节点后，不会再重新检查这个节点，导致了“错误答案”无法被修正。

读者可能会觉得上面的问题有点抽象,那么,就让我们结合这个样例,我们走一遍流程:

模拟流程

1.初始状态：此时只有节点1进入了堆中

示意图: dist 数组表示 源点1到其他点的距离
PQ 代表堆中的元素
dist = [0, ∞, ∞, ∞]  
PQ = { (1,0) }

2. 从 1 出发：

松弛操作：dist[2] = 6（从 1→2）

松弛操作：dist[3] = 5（从 1→3）

此时节点2,节点3都进入堆中

更新后的状态：

dist = [0, 6, 5, ∞]  
PQ = { (3,5), (2,6) }

3. 弹出 3(5)，标记 vis[3] = true，更新 dist[4]：

dist[4] = dist[3] + 1 = 5 + 1 = 6（从 3→4）

更新后的状态：

dist = [0, 6, 5, 6]  
PQ = { (2,6), (4,6) }

4: 弹出 2(6)，标记 vis[2] = true，并进行尝试：

尝试 2→3 时，dist[3] = dist[2] + (-4) = 6 + (-4) = 2，因为 vis[3] 是 true，所以没有更新。所以虽然 dist[3] =6, 但是,我们不会通过节点3去改变到达其他点的距离.

所以最后的结果为:

dist = [0, 6, 2, 6]

而我们希望的结果是:

dist = [0, 6, 2, 3]

通过上述的模拟演示,我们也能发现,在处理负权值图的最短路径时,Dijkstra 算法是有缺陷的

那么,我们可以选择 BF,SPFA,或者今天要介绍的Floyd 算法去解决,接下来,我们开始介绍Floyd算法

什么是Floyd算法

Floyd 算法，也称为Floyd-Warshall 算法。

Floyd 算法的最大特点就是简单直接，适用于任意权值（包括负权边，但不允许负权环），并且一次性可以算出任意两点之间的最短路径。

Floyd算法的核心思想

Floyd的思路可以归纳成一句话：

尝试用“中转点”去更新路径，看看能不能绕路更短！

假设我们有K个节点,此时我们要从节点 i 走到节点 j,算法会尝试把图中每一个节点 k 都当作“中转站”：如果 i 到 k 的距离 + k 到 j 的距离 < i 到 j 当前的距离，那么就用这个更短的路径更新！

所以每次循环的本质就是在问：

“如果路上多绕一个第 k 个点，会不会比原来的路线还要短呢？”

通过这样不断地尝试，最终我们可以得到任意两点之间的最短路径。

看到这里，细心的同学也许会发现：这不就是一个经典的动态规划问题吗？

我们可以用一个三维数组来描述这个问题：

状态表示

dp[k][i][j] 表示：在只允许经过节点 1 ~ k 这些点的情况下，从 i 到 j 的最短路径长度。

状态转移方程

对应的状态转移方程为:

dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j])

什么意思呢？
假设你已经计算好了在“前 k-1 个点”的限制下，
从 i 到 j 的最短路径。

当第 k 个节点加入图中，路径有两种情况：

1️⃣ 不经过 k，也就是：
还是用之前的路径 dp[k-1][i][j]

即保持现状,和之前只有k-1个节点时一模一样

2️⃣ 经过 k，路径变成：
dp[k-1][i][k] + dp[k-1][k][j]

将 i 到 j 的路径拆分成两段，先从 i 到 k，再从 k 到 j，看看这个组合的长度是否更短。

这里不涉及删除节点 i 或 j，只是用 k 当作中转点，把路径拆开看。

选择两者的最小值，更新当前的最短路径。

边界设置

那么,如何设置边界呢?

假设 i,j 有道路能直接相连,那么初始值 dp[0][i][j] 就是它们的边长,否则,就应该赋值为无穷大

代码实现

public static void floyd() {for (int k = 1; k <= N; k++) {         // 枚举中转点 kfor (int i = 1; i <= N; i++) {     // 枚举起点 ifor (int j = 1; j <= N; j++) { // 枚举终点 jdp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);}}}
}***N表示总的节点数量***

逻辑解释

这段代码的核心含义是：

1. 最外层循环 k：
依次尝试用每一个节点 k 作为“中转点”。

2. 中间层循环 i：
从起点 i 出发。

3. 内层循环 j：
目标是到达终点 j。

在每次循环中，程序都在思考：

“如果从 i 到 j 的路径，经过中转点 k，是否能更短？”

如果能更短，就更新路径长度：

接下来我们附上完整的代码:

import java.util.Arrays;
import java.util.Scanner;public class Floyd {static long[][] dp;static long INF = Long.MAX_VALUE / 2;  // 避免加法溢出static int N, M, Q;public static void floyd() {for (int k = 1; k <= N; k++) {for (int i = 1; i <= N; i++) {for (int j = 1; j <= N; j++) {dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);}}}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);N = scanner.nextInt();M = scanner.nextInt();Q = scanner.nextInt();// 初始化 Floyd 数组dp = new long[N + 1][N + 1];  //  N+1 是因为节点编号 1~Nfor (int i = 1; i <= N; i++) {Arrays.fill(dp[i], INF);  //  逐行填充 INFdp[i][i] = 0;  //  自己到自己距离为 0}// 读入 M 条边for (int i = 0; i < M; i++) {int u = scanner.nextInt();int v = scanner.nextInt();long w = scanner.nextLong();dp[u][v] = Math.min(dp[u][v], w);  //  处理多重边，取最小值dp[v][u] = Math.min(dp[v][u], w);  //  如果是无向图}// 执行 Floyd-Warshallfloyd();// 处理 Q 组查询for (int i = 0; i < Q; i++) {int st = scanner.nextInt();int ed = scanner.nextInt();if (dp[st][ed] == INF) {System.out.println(-1);  //  不可达，输出 -1} else {System.out.println(dp[st][ed]);}}scanner.close();}
}

举例说明

还是用我们刚刚那个图来验证:

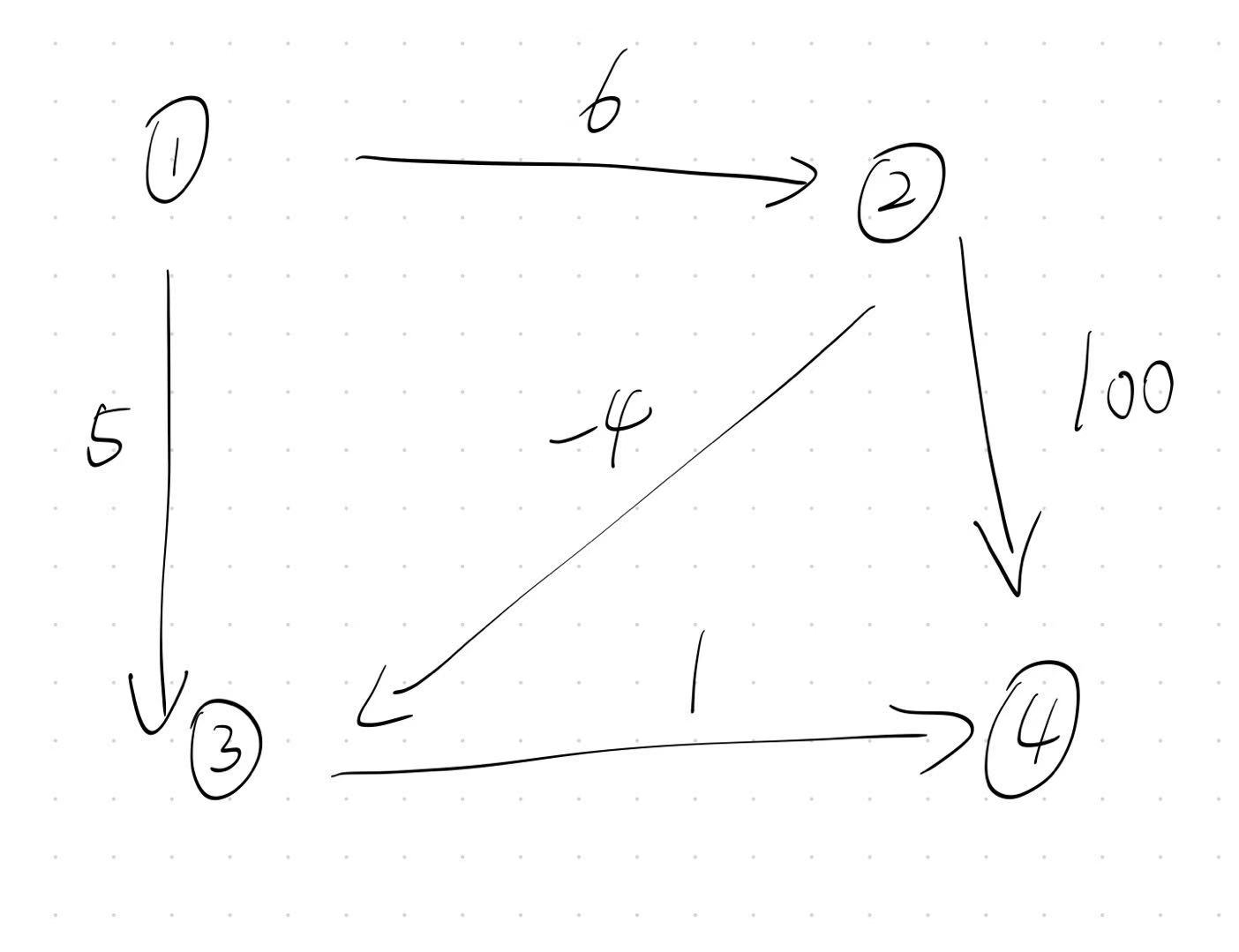
我们稍微修改一下示例代码,构成一个单向图,并且输出源点 1 到其他点的举例

输入数据:

import java.util.Arrays;
import java.util.Scanner;public class Floyd {static long[][] dp;static long INF = Long.MAX_VALUE / 2;  // 避免加法溢出static int N, M, Q;public static void floyd() {for (int k = 1; k <= N; k++) {for (int i = 1; i <= N; i++) {for (int j = 1; j <= N; j++) {dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);}}}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);N = scanner.nextInt();M = scanner.nextInt();
//        Q = scanner.nextInt();// 初始化 Floyd 数组dp = new long[N + 1][N + 1];  // ✅ N+1 是因为节点编号 1~Nfor (int i = 1; i <= N; i++) {Arrays.fill(dp[i], INF);  // ✅ 逐行填充 INFdp[i][i] = 0;  // ✅ 自己到自己距离为 0}// 读入 M 条边for (int i = 0; i < M; i++) {int u = scanner.nextInt();int v = scanner.nextInt();long w = scanner.nextLong();dp[u][v] = Math.min(dp[u][v], w);  // ✅ 处理多重边，取最小值}// 执行 Floyd-Warshallfloyd();for(int i = 1;i<=N;i++){System.out.print(dp[1][i]+" ");}
//        // 处理 Q 组查询
//        for (int i = 0; i < Q; i++) {
//            int st = scanner.nextInt();
//            int ed = scanner.nextInt();
//            if (dp[st][ed] == INF) {
//                System.out.println(-1);  //  不可达，输出 -1
//            } else {
//                System.out.println(dp[st][ed]);
//            }
//        }scanner.close();}
}

读者们复制进去后,能发现,结果为:

验证成功,使用 Floyd算法能解决该问题

Floyd算法的特点

支持负权边（前提：没有负权环）

不像 Dijkstra 那样只解决“单源”最短路径，可以一网打尽，计算任意两点之间的最短距离

通过一次Floyd 算法,我们可以得到图中任意两点的距离,没错,是随便两个点的距离!!!

算法结构简单，写起来很容易

适用于稠密图（边很多的图）

时间复杂度有一点高,是 O(n^3)，当节点数不大时非常方便好用,最好控制在300以内

结尾

博客的内容就暂时写到这里,系列下篇更新 BF算法和SPFA算法,

前言

Djikstra算法的缺陷

为什么无法解决负权图

模拟流程

什么是Floyd算法

Floyd算法的核心思想

状态表示

状态转移方程

边界设置

代码实现

逻辑解释

举例说明

Floyd算法的特点

结尾

相关文章：