分布类相关的可视化图像

目录

一、直方图（Histogram）

1.定义

2.特点

3.局限性

4.类型

5.应用场景

6.使用Python实现

二、密度图（Density Plot）

1.定义

2.特点

3.局限性

4.类型

5.应用场景

6.使用Python实现

三、箱线图（Box Plot）

1.定义

2.特点

3.局限性

4.类型

5.应用场景

6.使用Python实现

四、小提琴图（Violin Plot）

1.定义

2.特点

3.局限性

4.类型

5.应用场景

6.使用Python实现

五、热力图（Heatmap）

1.定义

2.特点

3.局限性

4.类型

5.应用场景

6.使用Python实现

六、蜂群图

1.定义

2.特点

3.局限性

4.类型

5.应用场景

6.使用Python实现

七、累积分布函数图（Cumulative Distribution Function,CDF图）

1.定义

2.特点

3.局限性

4.类型

5.应用场景

6.使用Python实现

八、总结

一、直方图（Histogram）

1.定义

        直方图是一种用于展示数据分布的柱状图。它将数据划分为若干个连续、不重叠的区间（称为“桶”或“bin”），并统计每个区间内的数据点数量。直方图通过柱状的高度来表示每个区间内的数据频数，从而直观地展示数据的分布情况。

2.特点

• 直观性：通过柱状图的形式，可以直观地展示数据的集中趋势、分散程度和偏态情况。

• 灵活性：可以通过调整bin的宽度和数量，更细致或更宏观地观察数据分布。

• 多用途：适用于单变量数据的分布分析，能够帮助识别数据中的异常值或分布的异常情况。

3.局限性

• 依赖bin的划分：bin的宽度和数量的选择会影响直方图的形状，可能导致对数据分布的误解。如果bin太宽，可能会掩盖数据的细节；如果bin太窄，可能会引入噪声。

• 不适用于小数据集：数据量较小时，直方图可能无法准确反映数据的真实分布。

• 无法展示连续分布：直方图只能展示数据在各个区间的频数，无法展示数据的连续分布情况。

4.类型

• 简单直方图：最基本的直方图，展示数据在各个区间的频数。

• 堆叠直方图：用于展示多个数据集的分布情况，通过堆叠的方式将不同数据集的柱状图叠加在一起。

• 并排直方图：用于展示多个数据集的分布情况，通过并排的方式将不同数据集的柱状图并排放置。

• 频率直方图：展示每个区间的频率（相对频数），而不是频数。

• 累积直方图：展示每个区间的累积频数或累积频率。

5.应用场景

• 数据分析：用于分析单变量数据的分布情况，例如考试成绩分布、商品价格分布、用户年龄分布等。

• 数据预处理：帮助识别数据中的异常值或数据分布的异常情况，为后续的数据处理提供依据。

• 质量控制：在生产过程中，用于分析产品质量指标的分布情况，判断生产过程是否稳定。

• 市场研究：分析消费者行为数据的分布情况，例如购买金额、购买频率等。

6.使用Python实现

        使用Matplotlib绘制直方图。

import matplotlib.pyplot as plt
import numpy as np# 示例数据
data = np.random.randn(1000)  # 生成1000个正态分布的随机数# 绘制简单直方图
plt.hist(data, bins=30, edgecolor='black', alpha=0.7, color='blue')
plt.title('Simple Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

        结果：生成一个简单直方图，展示数据的分布情况，柱状图的高度表示每个bin内的数据点数量。

         绘制堆叠直方图。堆叠直方图用于展示多个数据集的分布情况，通过堆叠的方式将不同数据集的柱状图叠加在一起。

#堆叠直方图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data1 = np.random.randn(1000)
data2 = np.random.randn(1000) + 2  # 偏移2个单位
# 绘制堆叠直方图
plt.hist([data1, data2], bins=30, stacked=True, edgecolor='black', label=['Data 1', 'Data 2'])
plt.title('Stacked Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.legend()
plt.show()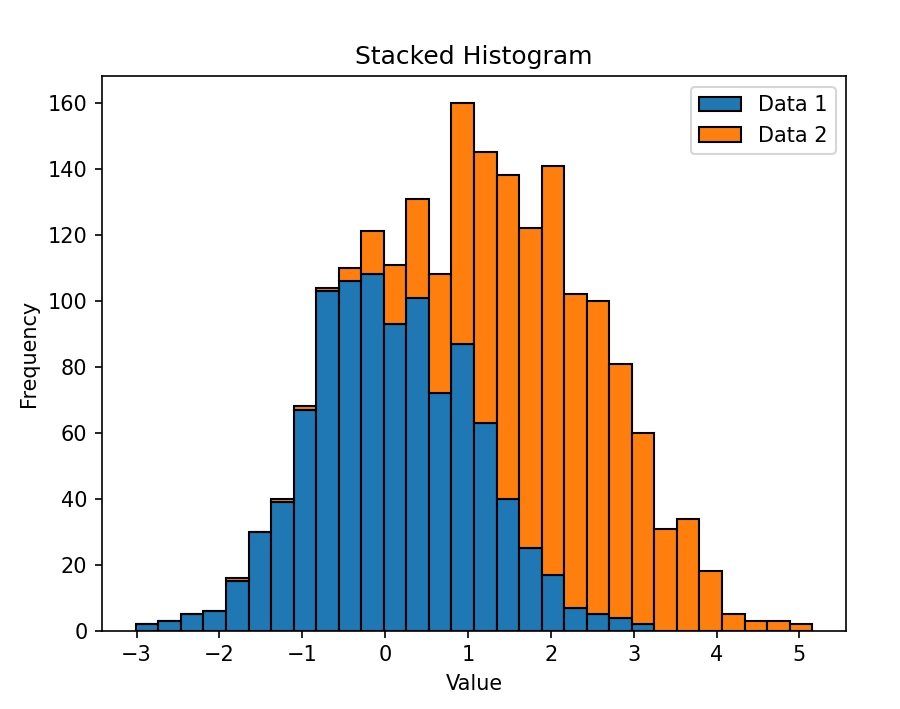

        结果：生成一个堆叠直方图，展示两个数据集的分布情况，不同数据集的柱状图通过堆叠的方式叠加在一起。

二、密度图（Density Plot）

1.定义

        密度图是一种基于核密度估计（Kernel Density Estimation, KDE）的可视化方法，用于展示数据的概率密度分布。它通过平滑处理数据点，生成一条连续的曲线，从而更直观地展示数据的分布特征。密度图的核心思想是将每个数据点视为一个“核”，并通过核函数对数据点进行平滑处理，最终得到一个连续的概率密度函数。

2.特点

• 平滑性：相比直方图，密度图更加平滑，能够更直观地展示数据的连续分布情况。

• 灵活性：可以通过调整核函数和带宽参数来优化密度曲线的形状，以更好地适应数据的分布特征。

• 直观性：能够清晰地展示数据的集中趋势、分散程度和偏态情况。

• 多用途：适用于展示连续数据的概率分布，尤其适用于数据点较多且分布较为复杂的情况。

3.局限性

• 依赖参数选择：核函数和带宽参数的选择会影响密度曲线的形状，可能导致对数据分布的误解。如果带宽过大，可能会掩盖数据的真实分布；如果带宽过小，可能会引入噪声。

• 计算复杂度：对于大数据集，核密度估计的计算复杂度较高，可能会影响性能。

• 不适用于离散数据：密度图主要用于展示连续数据的分布，对于离散数据可能不太适用。

4.类型

• 单变量密度图：用于展示单个变量的概率密度分布。

• 多变量密度图：用于展示多个变量的概率密度分布，可以通过堆叠或并排的方式展示不同变量的密度曲线。

• 二维密度图：用于展示两个变量的联合概率密度分布，通常通过等高线图或热力图来表示。

5.应用场景

• 数据分析：用于展示连续数据的概率分布，帮助识别数据的集中趋势、分散程度和偏态情况。

• 数据比较：可以用于比较不同组数据的分布差异，例如不同性别或不同年龄段的收入分布。

• 机器学习：在数据预处理阶段，帮助理解数据的分布特征，为后续的建模提供依据。

• 统计分析：用于展示数据的分布情况，辅助进行假设检验和模型拟合。

6.使用Python实现

        使用Matplotlib绘制单变量密度图

#密度图
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde# 示例数据
data = np.random.randn(1000)  # 生成1000个正态分布的随机数# 计算核密度估计
kde = gaussian_kde(data)
x = np.linspace(min(data), max(data), 1000)
density = kde(x)# 绘制密度图
plt.plot(x, density, color='blue', label='Density')
plt.title('Density Plot')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

        结果：生成一条平滑的密度曲线，展示数据的概率密度分布。

        使用Seaborn绘制多变量密度图。Seaborn的kdeplot函数支持多变量数据，可以通过堆叠或并排的方式展示不同变量的密度曲线。

#多变量密度图
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt  # 添加这行导入# 示例数据
data1 = np.random.randn(1000)  # 生成1000个正态分布的随机数
data2 = np.random.randn(1000) + 2  # 偏移2个单位# 绘制多变量密度图
sns.kdeplot(data1, fill=True, color='blue', label='Data 1')
sns.kdeplot(data2, fill=True, color='orange', label='Data 2')
plt.title('Multi - variable Density Plot')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

        结果：生成两条平滑的密度曲线，分别展示两个数据集的概率密度分布，并填充曲线下的区域。

三、箱线图（Box Plot）

1.定义

        箱线图（Box Plot），也称为箱须图（Box-and-Whisker Plot），是一种用于展示一组数据的五数概括（最小值、第一四分位数、中位数、第三四分位数和最大值）的可视化方法。它通过一个矩形框（箱体）和若干条线（须线）来表示数据的分布范围和集中趋势。箱线图能够直观地展示数据的中位数、四分位数范围（IQR）、异常值以及数据的偏态情况。

2.特点

• 五数概括：清晰地展示数据的最小值、第一四分位数（Q1）、中位数（Q2）、第三四分位数（Q3）和最大值。

• 直观性：通过箱体的大小和位置，可以直观地比较不同组数据的分布差异。

• 异常值检测：能够识别数据中的异常值（通常定义为超出1.5倍四分位距范围的点）。

• 偏态展示：通过箱体和须线的不对称性，可以直观地判断数据的偏态情况。

3.局限性

• 信息有限：仅展示五数概括，无法反映数据的详细分布情况，例如双峰分布等。

• 依赖数据量：对于小数据集，箱线图可能无法准确反映数据的真实分布。

• 异常值定义主观性：异常值的定义（通常是1.5倍IQR）是主观的，可能不适用于所有数据集。

4.类型

• 简单箱线图：展示单组数据的五数概括。

• 分组箱线图：用于展示多组数据的分布情况，通过并排的方式展示不同组的箱线图。

• 带点箱线图：在箱线图的基础上，展示原始数据点，便于更直观地观察数据分布。

5.应用场景

• 数据分析：用于分析数据的分布特征，尤其是数据的集中趋势和离散程度。

• 数据比较：在多组数据的比较中，能够快速识别出异常值和数据分布的偏态情况。

• 质量控制：在生产过程中，用于分析产品质量指标的分布情况，判断生产过程是否稳定。

• 统计分析：用于展示数据的分布情况，辅助进行假设检验和模型拟合。

6.使用Python实现

        使用Matplotlib绘制简单箱线图

        结果：生成一个简单箱线图，展示数据的五数概括，箱体表示四分位数范围，须线表示数据的分布范围，点表示异常值。

        使用Seaborn绘制分组箱线图

import seaborn as sns
import numpy as np
import pandas as pd# 示例数据
data1 = np.random.randn(100)
data2 = np.random.randn(100) + 2  # 偏移2个单位
df = pd.DataFrame({'Value': np.concatenate([data1, data2]),'Group': ['Group 1'] * 100 + ['Group 2'] * 100})# 绘制分组箱线图
sns.boxplot(x='Group', y='Value', data=df, palette='Set2')
plt.title('Grouped Box Plot')
plt.ylabel('Value')
plt.show()

        结果：生成一个分组箱线图，展示两组数据的分布情况，通过并排的方式展示不同组的箱线图。

四、小提琴图（Violin Plot）

1.定义

        小提琴图是一种结合了箱线图（Box Plot）和密度图（Density Plot）的可视化工具。它在箱线图的基础上，增加了两侧的密度曲线，用于展示数据的概率密度分布。小提琴图通过箱线图展示数据的五数概括（最小值、第一四分位数、中位数、第三四分位数和最大值），并通过密度曲线展示数据的连续分布情况。

2.特点

• 综合展示：结合了箱线图和密度图的优点，既能展示数据的五数概括，又能展示数据的连续分布情况。

• 直观性：通过小提琴的宽度，可以直观地看出数据在不同值范围内的密度大小，帮助识别数据的集中趋势和离散程度。

• 异常值检测：与箱线图类似，小提琴图也可以展示异常值。

• 多组数据比较：可以并排展示多组数据的小提琴图，便于比较不同组数据的分布差异。

3.局限性

• 依赖参数选择：密度曲线的形状依赖于核函数和带宽参数的选择，可能导致对数据分布的误解。

• 信息过载：在展示多组数据时，小提琴图可能会显得过于拥挤，尤其是当数据组数较多时。

4.类型

• 简单小提琴图：展示单组数据的分布情况。

• 分组小提琴图：并排展示多组数据的分布情况，便于比较不同组之间的差异。

• 堆叠小提琴图：将多组数据的小提琴图堆叠在一起，展示数据的层次结构。

5.应用场景

• 数据分析：用于展示复杂数据的分布情况，尤其适用于数据分布不均匀或存在多个峰值的情况。

• 数据比较：在多组数据的比较中，能够更全面地展示数据的分布特征和差异。

• 统计分析：用于展示数据的分布情况，辅助进行假设检验和模型拟合。

• 机器学习：在数据预处理阶段，帮助理解数据的分布特征，为后续的建模提供依据。

6.使用Python实现

使用Matplotlib绘制简单小提琴图

#小提琴图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data = np.random.randn(100)  # 生成100个正态分布的随机数
# 绘制简单小提琴图
plt.violinplot(data, showmeans=True, showmedians=True)
plt.title('Simple Violin Plot')
plt.ylabel('Value')
plt.show()

        结果：生成一个简单小提琴图，展示数据的五数概括和密度分布情况。

        使用Matplotlib绘制分组小提琴图

import matplotlib.pyplot as plt
import numpy as np# 示例数据
data1 = np.random.randn(100)
data2 = np.random.randn(100) + 2  # 偏移2个单位
data = [data1, data2]# 绘制分组小提琴图
plt.violinplot(data, showmeans=True, showmedians=True)
plt.title('Grouped Violin Plot')
plt.ylabel('Value')
plt.xticks([1, 2], ['Group 1', 'Group 2'])
plt.show()

        结果：生成一个分组小提琴图，展示两组数据的分布情况，通过并排的方式展示不同组的小提琴图。

五、热力图（Heatmap）

1.定义

        热力图是一种用于展示二维数据分布的可视化方法，通过颜色的变化来表示数据的大小或密度。它通常用于展示矩阵数据或二维表格数据，例如相关性矩阵、地理数据分布、时间序列数据等。热力图的核心思想是将数据映射到颜色的渐变上，从而直观地展示数据的分布模式和相关性。

2.特点

• 直观性：通过颜色的渐变，可以快速识别数据的高低和聚集区域。

• 多用途：适用于展示相关性矩阵、地理数据分布、时间序列数据等多种二维数据。

• 灵活性：可以通过调整颜色映射、添加注释等方式增强可视化效果。

• 数据比较：可以同时展示多个变量之间的关系，便于比较和分析。

3.局限性

• 信息过载：当数据量较大或变量较多时，热力图可能会显得过于拥挤，难以清晰地展示细节。

• 依赖颜色选择：颜色映射的选择会影响热力图的可读性，不恰当的颜色选择可能导致误解。

• 不适合展示非矩阵数据：热力图主要用于展示矩阵数据，对于非矩阵数据可能不太适用。

4.类型

• 相关性热力图：用于展示变量之间的相关性，通常用于统计分析。

• 地理热力图：用于展示地理数据的分布情况，例如人口密度、温度分布等。

• 时间序列热力图：用于展示时间序列数据的变化趋势，例如每日温度、股票价格等。

• 矩阵热力图：用于展示任意二维矩阵数据，例如用户行为数据、基因表达数据等。

5.应用场景

• 地理分析：用于展示地理数据的分布情况，例如人口密度、温度分布等。

• 时间序列分析：用于展示时间序列数据的变化趋势，帮助识别周期性和异常点。

• 用户行为分析：用于展示用户行为数据的分布情况，例如网站访问量、用户点击率等。

6.使用Python实现

        使用Matplotlib绘制相关性热力图

import matplotlib.pyplot as plt
import numpy as np# 示例数据：生成一个相关性矩阵
data = np.random.randn(10, 10)
corr_matrix = np.corrcoef(data)# 绘制热力图
plt.imshow(corr_matrix, cmap='coolwarm', interpolation='nearest')
plt.colorbar(label='Correlation')
plt.title('Correlation Heatmap')
plt.xlabel('Variable Index')
plt.ylabel('Variable Index')
plt.show()

        结果：生成一个相关性热力图，展示变量之间的相关性。颜色的深浅表示相关性的强弱。

        使用Seaborn绘制地理热力图

import seaborn as sns
import numpy as np
import pandas as pd# 示例数据：生成一个地理数据矩阵
data = np.random.rand(10, 10) * 100  # 假设数据范围为0到100
df = pd.DataFrame(data, columns=[f"Long {i}" for i in range(10)],index=[f"Lat {i}" for i in range(10)])# 绘制地理热力图
sns.heatmap(df, annot=True, fmt=".1f", cmap='viridis', linewidths=0.5)
plt.title('Geographical Heatmap')
plt.show()

         结果：生成一个地理热力图，展示地理数据的分布情况。颜色的深浅表示数据的大小。

六、蜂群图

1.定义

        蜂群图是一种点图的变体，它通过将数据点沿着一个轴排列，并在另一个轴上进行微小的偏移，以避免重叠。这种排列方式使得每个数据点都能清晰地展示出来，同时保留了数据的分布信息。蜂群图特别适合展示具有多个类别的数据分布情况。

2.特点

• 清晰展示数据点：通过微小的偏移，避免了数据点的重叠，使得每个数据点都能清晰地展示出来。

• 保留分布信息：与箱线图或小提琴图相比，蜂群图保留了每个数据点的具体信息，而不是仅仅展示统计量。

• 适用于小数据集：对于数据量较小的数据集，蜂群图能够有效地展示数据的分布情况。

• 灵活性：可以通过调整点的大小、颜色和形状，增强可视化效果。

3.局限性

• 不适用于大数据集：当数据量较大时，蜂群图可能会显得过于拥挤，难以清晰地展示每个数据点。

• 依赖数据分布：如果数据分布过于密集，蜂群图可能会失去其优势，甚至导致视觉上的混乱。

• 信息有限：虽然蜂群图能够展示每个数据点，但它无法像箱线图或小提琴图那样直接展示数据的统计量（如中位数、四分位数等）。

4.类型

• 简单蜂群图：展示单组数据的分布情况。

• 分组蜂群图：并排展示多组数据的分布情况，便于比较不同组之间的差异。

• 堆叠蜂群图：将多组数据的蜂群图堆叠在一起，展示数据的层次结构。

5.应用场景

• 数据分析：用于展示数据的分布情况，特别适合小数据集。

• 数据比较：在多组数据的比较中，能够清晰地展示每个数据点的位置，便于识别差异。

• 统计分析：用于展示数据的分布情况，辅助进行假设检验和模型拟合。

• 机器学习：在数据预处理阶段，帮助理解数据的分布特征，为后续的建模提供依据。

6.使用Python实现

        使用Matplotlib绘制简单蜂群图

import matplotlib.pyplot as plt
import numpy as np# 示例数据
data = np.random.randn(500)  # 生成500个正态分布的随机数# 计算偏移量
jitter = np.random.uniform(-0.1, 0.1, size=len(data))# 绘制蜂群图
plt.scatter(jitter, data, alpha=0.7, color='blue')
plt.title('Simple Beeswarm Plot')
plt.xlabel('Category')
plt.ylabel('Value')
plt.show()

        结果：生成一个简单蜂群图，展示数据的分布情况，每个数据点通过微小的偏移避免重叠。

        使用Seaborn绘制分组蜂群图

import seaborn as sns
import matplotlib.pyplot as plt# 加载Seaborn自带的tips数据集
tips = sns.load_dataset('tips')# 绘制蜂群图，按' day'（星期几）分组，展示'tip'（小费金额），并根据'smoker'（是否吸烟）进行颜色区分
sns.swarmplot(x='day', y='tip', hue='smoker', data=tips)plt.title('Grouped Beeswarm Plot of Tips')
plt.xlabel('Day of the Week')
plt.ylabel('Tip Amount')
plt.legend(title='Smoker')
plt.show()

        结果：生成一个分组蜂群图，展示四组数据的分布情况，通过并排的方式展示不同组的蜂群图。

七、累积分布函数图（Cumulative Distribution Function,CDF图）

1.定义

        累计分布图（CDF）是一种用于展示数据分布的函数图，它表示数据值小于或等于某个特定值的概率。CDF是一个单调递增的函数，其值域在0,1之间。对于一个随机变量X，其累计分布函数F(x)定义为： F(x)=P(X≤x) CDF图通过绘制x值与对应的F(x)值，直观地展示了数据的分布情况。

2.特点

• 直观性：CDF图能够直观地展示数据值的累积概率，帮助理解数据的分布范围和集中程度。

• 单调性：CDF图是一个单调递增的函数，其值域在0,1之间，便于比较不同数据集的分布。

• 灵活性：可以通过调整数据的分组或分段，展示不同粒度的累积分布情况。

3.局限性

• 信息有限：CDF图主要展示累积概率，无法像直方图或密度图那样直观地展示数据的具体分布形状。

• 依赖数据量：对于小数据集，CDF图可能不够平滑，难以准确反映数据的真实分布。

• 不适用于多变量比较：CDF图主要用于单变量数据的分析，对于多变量数据的比较，可能需要绘制多个CDF图，导致信息过载。

4.类型

• 简单CDF图：展示单个数据集的累积分布情况。

• 分组CDF图：并排或堆叠展示多个数据集的累积分布情况，便于比较不同组之间的差异。

• 经验CDF图：基于实际数据计算的CDF图，通常用于展示样本数据的分布情况。

5.应用场景

• 数据分析：用于展示数据的分布范围和累积概率，帮助识别数据的集中趋势和离散程度。

• 统计分析：用于计算分位数（如中位数、四分位数等），评估数据的偏态和离散程度。

• 质量控制：在生产过程中，用于分析产品质量指标的分布情况，判断生产过程是否稳定。

6.使用Python实现

        使用Matplotlib绘制简单CDF图

import matplotlib.pyplot as plt
import numpy as np# 示例数据
data = np.random.randn(1000)  # 生成1000个正态分布的随机数# 计算累积分布函数
counts, bin_edges = np.histogram(data, bins=30)
cdf = np.cumsum(counts) / np.sum(counts)# 绘制CDF图
plt.plot(bin_edges[1:], cdf, marker='.', linestyle='-', color='b')
plt.title('Cumulative Distribution Function (CDF)')
plt.xlabel('Value')
plt.ylabel('Cumulative Probability')
plt.grid(True)
plt.show()

        结果：生成一个简单的CDF图，展示数据的累积分布情况

        使用Seaborn绘制分组经验CDF图

import seaborn as sns
import numpy as np
import pandas as pd# 示例数据
data1 = np.random.randn(1000)
data2 = np.random.randn(1000) + 2  # 偏移2个单位
df = pd.DataFrame({'Value': np.concatenate([data1, data2]),'Group': ['Group 1'] * 1000 + ['Group 2'] * 1000})# 绘制分组经验CDF图
sns.ecdfplot(data=df, x='Value', hue='Group', palette='Set2')
plt.title('Grouped Empirical Cumulative Distribution Function (ECDF)')
plt.xlabel('Value')
plt.ylabel('Cumulative Probability')
plt.grid(True)
plt.show()

        结果：生成一个分组经验CDF图，展示两组数据的累积分布情况。Seaborn会自动处理数据的分组和累积概率的计算。

八、总结

图表 类型	特点	适用场景	局限性
直方图	直观呈现数据频数分布，可看出数据集中和分散情况	展示单变量数据分布，如学生成绩区间分布、产品尺寸分布	分组方式影响展示效果，对数据变化趋势展示不足
密度图	平滑展示数据分布，可对比多组数据分布形状，不受分组影响	分析连续型数据分布，如不同地区气温分布对比	难以精确读取具体数值，对数据量小的情况可能不准确
箱线图	可直观展示数据分布范围、偏态、离散程度及异常值，便于多组数据比较	比较多组数据分布，如不同班级成绩分布对比	不能详细展示数据分布形状，对分布细节展示有限
小提琴图	兼具箱线图和密度图优势，全面展示数据分布特征，如中心位置、离散程度、分布形状	展示多组数据分布特征，对比不同类别数据分布	绘制相对复杂，数据量过大时可能视觉上较杂乱
热力图	能快速展示数据间差异和相似性，直观呈现数据分布模式	展示矩阵数据（如相关性矩阵、时间序列数据矩阵）、地理空间数据分布，如店铺在不同区域的热度分布	颜色映射可能造成视觉误差，难以展示数据具体数值
蜂群图	可展示大量数据点分布，能清晰看到每个数据点位置，体现数据实际取值	展示分组数据分布，查看组内数据离散情况，如不同部门员工绩效得分分布	数据点过多时可能重叠，影响观察，不适合展示数据整体分布趋势
累积分布图	可直观了解数据在某个值以下的累积概率，判断数据分布特征，如是否符合某种理论分布	检验数据分布类型，分析数据累积概率，如判断产品寿命是否符合指数分布	不能展示数据分布细节，如峰值位置等