当前位置：首页 > news >正文

【深度学习—李宏毅教程笔记】各式各样的 Attention

news 来源：原创 2025/8/1 20:16:05

一、普通 Self-Attention 的痛点

二、对 Self-Attention 的优化方式

1、Local Attention / Truncated Attention

2、Stride Attention

3、Global Attention

4、知名的 Self-Attention 的变形的应用

（1）Longformer

（2）Big Bird

5、data driven 的方式决定注意力的计算范围

（1）第一种方法是聚类的方法

（2）第二种方法是用训练的方式

6、Linformer—对原 Attention 矩阵进行去冗

7、从矩阵运算方面优化 Self-Attention 的计算量

（1）先回顾一下 Self-Attention 的矩阵运算过程

（2）先来一个简单的，假设忽略 softmax 这个非线性的过程

（3）放回 softmax 后，如何简化 Attention 的运算呢？

（4）这里的核方法如何实现？

8、Synthesizer — 不使用 k 和 q 来生成注意力矩阵

9、一些相关的丢掉 Attention 的研究

三、总结

一、普通 Self-Attention 的痛点

普通 Self-Attention 的痛点就是在计算注意力矩阵时的计算量会随着序列长度的上升而迅速上升。特别是图像方面，比如说一个 256×256 的图像，那么序列的长度 N 就是 $256^{2}$ ，那么注意力矩阵的大小就是 $256^{2}$ × $256^{2}$ ，如下图：

所以简化注意力矩阵的运算量，优化 Attention 的计算就成了一个很必要的事情，特别是图像方面。

Self-Attention 的计算量知识整个模型计算量的一部分，假设模型是 Transformer ，Self-Attention所带来的计算量也只是模型整体计算量的一部分，Transformer 的计算量还包括 Feed Forward 、softmax 等，序列的长度越长，Self-Attention 的计算量在整个模型中的占比越大。所以说，对 Self-Attention 的优化最早是出现在影像处理方面。

二、对 Self-Attention 的优化方式

在计算 Self-Attention 时，一般是计算所有输入序列之间的 Attention ，构造 Attention 矩阵，但其实序列很长时，比较远的元素之间的 Attention 的计算可能是没有必要的。

1、Local Attention / Truncated Attention

Truncated：截断

Local：当地

即只计算序列中每个元素与其相邻的元素的 Attention ，其他的 Attention 不进行计算，如下图：

和 cnn 很像，可以加快运算，但不一定效果好。

2、Stride Attention

Stride ：跨

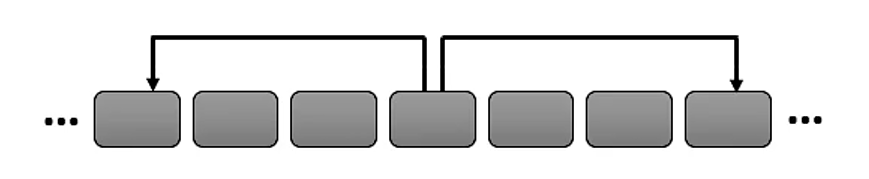
中间空着格做 Attention ，类似于空洞卷积。

3、Global Attention

增加特别的 token 到原序列，这些特别的 token 做两件事情：

它们的 Query（q值）去 “询问” 所有 token 的 Key（k值）。
它们的 Key 被所有 token 的 Query 去“询问”。

特别的 token 可以额外加几个，或者让原序列的某几个设为特殊的 token ，如下图所示：

要计算的 Attention 为：

4、知名的 Self-Attention 的变形的应用

（1）Longformer

地址：（这里）

其中的 Attention ：

用了很多种 Attention 的变形

（2）Big Bird

这个名字可能是作者随便起的名字。

地址：（这里）

其中的 Attention ：

5、data driven 的方式决定注意力的计算范围

data driven：数据驱动

前边介绍的注意力的计算范围都是人为确定的范围，下面将介绍数据驱动的注意力的计算范围。

数据驱动的方式就是将可能注意力小的地方设为零，只计算注意力可能大的地方，即：

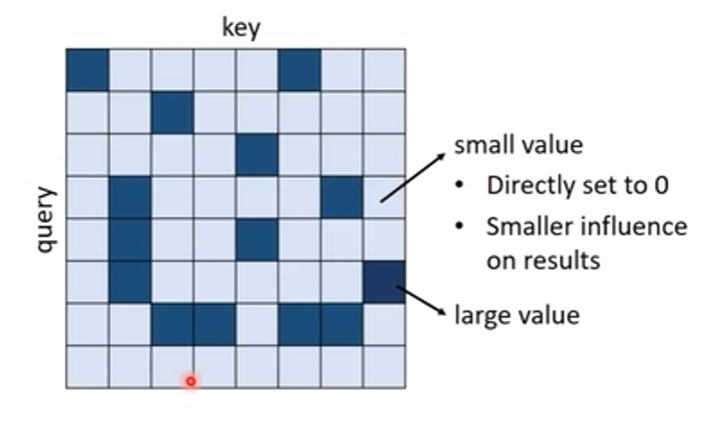
如何知道哪些地方注意力小，哪些地方注意力大呢？

（1）第一种方法是聚类的方法

在一些论文中，（论文 Reformer（这里）、论文Routing Transformer（这里）），使用 Clustering（聚类）的方法，让所有 token 的 query 值和 Key 值放在一起进行聚类，只让在一个簇内的计算 Attention ，其他的都设为 0，这样的话，聚类的计算会带来很大的计算量吗？对聚类的计算有很多的优化方式，上面的两篇论文就是对聚类的优化方式不一样，如下图：

（2）第二种方法是用训练的方式

即用另一个 NN 模型 “ 硬 train 一发 ”。

6、Linformer—对原 Attention 矩阵进行去冗

在计算出的 Attention 矩阵中，很多信息都是冗余的，Linformer 实现了对冗余信息的消除，不计算 full attention matrix ，只计算重要的部分。

论文Linformer：（这里）

具体做法是什么呢？

实际上，总共有 N 个 Key，从其中挑选 K 个作为代表来和 query 计算注意力，同样也挑出相应的 K 个 value 进行后续的计算得到输出，如下图：

怎么选出有代表性的 Key 呢？

有不同种方式：

在 Compressed Attention 中（论文：（这里）），仍然是通过 train 的方式，通过 cnn 将长的序列 Key 变成短的，如下图

在 Linformer 中（论文：（这里）），将序列 Key 乘上一个矩阵，让它变短（进行 K 次线性变换），如下图

7、从矩阵运算方面优化 Self-Attention 的计算量

（1）先回顾一下 Self-Attention 的矩阵运算过程

（2）先来一个简单的，假设忽略 softmax 这个非线性的过程

忽略 softmax 这个非线性的过程后，这个矩阵运算过程就变成了：

其中的额 d 是序列中每个 token 的维度，也就是编码的长度，N 是序列的长度。

这个矩阵运算过程是：

首先输入 $I$ 乘上参数矩阵 $W^{q}$ 、 $W^{k}$ 、 $W^{v}$ 得到三个矩阵 $Q$ 、 $K$ 、 $V$ ，随后从右到左计算 $K^{T}\cdot Q$ ，得到结果后再左乘上矩阵 $V$ 。

这个运算过程是可能可以简化的，即先把 $V$ 和 $K^{T}$ 相乘，得到结果再和 $Q$ 相乘，为什么呢？

解决为什么？

对于 $K^{T}\cdot Q$ ，乘法运算的次数为 $N\cdot d\cdot N$ ，得到的矩阵的形状为 $N\cdot N$

然后再与 $V$ 相乘，乘法运算的次数为 ${d}'\cdot N\cdot N$

所有总的乘法次数为 $(d+{d}') N^{2}$

同理先把 $V$ 和 $K^{T}$ 相乘，得到结果再和 $Q$ 相乘的乘法次数为： $2{d}'dN$

所以说，当序列长度 $N$ 很大时。改变矩阵的运算次序可以简化 Attention 的计算量。

（3）放回 softmax 后，如何简化 Attention 的运算呢？

视频链接：（这里）（时间 0：47：00 ~ 1：04：00）

核心思想：没放回 softmax 时，全部都是线性变换，放回 softmax 后，加入了非线性变换，这时使用 核方法 ，让非线性变回线性。在计算 $b^{1}$ 、 $b^{2}$ 、 $b^{3}$ 、 $\cdot \cdot \cdot$ 过程中，中间有很多计算不需要重复计算，可简化。

这里的 softmax 是对注意力矩阵进行的，所以 $b^{1}$ 的计算过程如下：

这时只要找到一个函数 $\phi$ 使得： $exp(q\cdot k)\approx \phi (q)\cdot \phi (k)$ ，那么 $b^{1}$ 的计算可化为：

...

后续太繁琐了，见视频。

（4）这里的核方法如何实现？

有很多种方法，在不同的论文中实现：

论文 Efficient attention ：（这里）

论文 Linear Transformer ：（这里）

论文 Random Feature Attention ：（这里）

论文 Performer ：（这里）

8、Synthesizer — 不使用 k 和 q 来生成注意力矩阵

如上图，和普通 Self-Attention 一样，但左侧的注意力矩阵不是 k 和 q 产生的。那是如何得到的呢？

一种方法是直接 train 得到，即 “ 硬 train 一发 ”

另一种方法是把这个矩阵当作 network 的一部分，把它当作 network 的参数，其中的 $N$ × $N$ 个数值就是 network 的 $N$ × $N$ 个参数，即不再计算 Attention 矩阵，直接用 network 的参数代替。

9、一些相关的丢掉 Attention 的研究

论文：

Fnet: Mixing tokens with Fourier transforms：（这里）

Pay Attention to MLPs：（这里）

MLP-Mixer: An all-MLP Architecture for Vision：（这里）

三、总结

关于 Attention 相关的改进优化都在下面这个图中：

圈的大小代表使用的多少，纵轴代表性能，横轴代表速度（越往右越快）

Big Bird：把不同人设计的局部注意力矩阵放在一起组成多头注意力机制
Local Attention：只计算部分的注意力矩阵，其他不计算设为 0 ，速度很快，性能不好
Synthesizer：新的框架，即不使用 k 和 q 来生成注意力矩阵，其他与普通注意力机制一样
Reformer：对 k 和 q 做聚类，只计算聚类内的注意力分数，图中可见其速度和性能都不如普通transformer
Sinkform：直接用一个 network 来决定要计算哪些注意力分数，数据驱动，性能不如transformer，但速度比较快
Linformer：只选一些有代表性的 Key，性能比 Transformer 差了一点，但速度快很多
Linear Transformer：从先算 $k\cdot q$ ，改为先算 $v\cdot k$ ，即从矩阵运算方面加速 Attention 的计算，性能比 Transformer 差了一点，但速度快很多
Performer：从先算 $k\cdot q$ ，改为先算 $v\cdot k$ ，即从矩阵运算方面加速 Attention 的计算，性能比 Transformer 差了一点，但速度快很多

一、普通 Self-Attention 的痛点

二、对 Self-Attention 的优化方式

1、Local Attention / Truncated Attention

2、Stride Attention

3、Global Attention

4、知名的 Self-Attention 的变形的应用

（1）Longformer

（2）Big Bird

5、data driven 的方式决定注意力的计算范围

（1）第一种方法是聚类的方法

（2）第二种方法是用训练的方式

6、Linformer—对原 Attention 矩阵进行去冗

7、从矩阵运算方面优化 Self-Attention 的计算量

（1）先回顾一下 Self-Attention 的矩阵运算过程

（2）先来一个简单的，假设忽略 softmax 这个非线性的过程

（3）放回 softmax 后，如何简化 Attention 的运算呢？

（4）这里的核方法如何实现？

8、Synthesizer — 不使用 k 和 q 来生成注意力矩阵

9、一些相关的丢掉 Attention 的研究

三、总结

相关文章：