【数据结构】红黑树
红黑树( R e d B l a c k T r e e Red\ Black\ Tree Red Black Tree)是一种自平衡二叉搜索树,也可以看作一种特化的 A V L AVL AVL 树(通过颜色规则来实现自平衡功能),都是在进行插入和删除操作时通过特定操作保持二叉搜索树的平衡,从而获得 O ( log N ) O(\log N) O(logN) 的查找性能,在 C C C++ S T L STL STL 标准库中, m a p map map 和 s e t set set 的底层结构就是红黑树。
文章目录
- 一、红黑树的概念
- 1. 基本规则
- 2. 红黑树的效率
- 二、红黑树的基本操作
- 1. 基本结构
- 2. 插入操作
- 2.1 插入的过程
- 2.2 情况一:变色
- 2.2 情况二:旋转+变色
- (1) 单旋+变色
- (2) 双旋+变色
- 3. 查找操作
- 4. 验证操作
- 三、红黑树的实现
- 总结
一、红黑树的概念
红黑树是一棵二叉搜索树,他的每个结点增加一个存储位来表示结点的颜色,可以是红色或者黑色。通过对任何一条从根到叶子的路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出 2 2 2 倍,因而是接近平衡的。

1. 基本规则
红黑树( R B − t r e e RB-tree RB−tree)不仅仅是一个二叉搜索树,其要求和 A V L AVL AVL 树类似,要达到自平衡的效果,因此,其通过约束每个结点的颜色来实现平衡,也就是说必须满足以下四条规则:
【规则 1 1 1】每个结点不是红色就是黑色。
【规则 2 2 2】根结点是黑色的。
【规则 3 3 3】如果一个结点是红色的,则它的两个孩子结点必须是黑色的,也就是说任意一条路径不会有连续的红色结点。
【规则 4 4 4】对于任意一个结点,从该结点到其所有 N U L L NULL NULL 结点的简单路径上,均包含相同数量的黑色结点。
比如说,下图就是一个经典的红黑树(每条路径的黑色结点个数都为 2 2 2 个):

思考一下,红黑树如何确保最长路径不超过最短路径的 2 2 2 倍的呢?
- 由【规则 4 4 4】可知,从根到 N U L L NULL NULL 结点的每条路径都有相同数量的黑色结点,所以极端场景下,最短路径就是全是黑色结点的路径,假设每条路径的黑色结点数量为 x x x 个,最短路径长度为 b h bh bh( b l a c k h e i g h t black\ height black height),那么 b h = x bh=x bh=x。

- 由【规则 2 2 2】和【规则 3 3 3】可知,任意一条路径不会有连续的红色结点,所以极端场景下,最长路径就是一黑一红间隔组成的路径,那么最长路径的长度为 2 ⋅ b h 2\cdot bh 2⋅bh。

- 综合红黑树的 4 4 4 点规则而言,理论上的全黑最短路径和一黑一红的最长路径并不是在每棵红黑树都存在的。假设任意一条从根结点到 N U L L NULL NULL 结点的路径长度为 h h h,那么 b h ≤ h ≤ 2 ⋅ b h bh \le h \le 2\cdot bh bh≤h≤2⋅bh。

2. 红黑树的效率
红黑树的表达相对 A V L AVL AVL 树要抽象一些, A V L AVL AVL 树通过高度差直观的控制了平衡,红黑树则通过 4 4 4 条规则的颜色约束,间接的实现了近似平衡,他们效率都是同一档次(时间复杂度都是 O ( log N ) O(\log N) O(logN)),但是相对而言,插入相同数量的结点,红黑树的旋转次数是更少的,因为他对平衡的控制没那么严格。

假设 N N N 是红黑树树中结点数量, h h h 最短路径的长度,那么就可以得到:
2 h − 1 ≤ N ≤ 2 2 ⋅ h − 1 2^h − 1 \le N \le 2^{2\cdot h} − 1 2h−1≤N≤22⋅h−1
由此推出:
h ≈ log N h ≈ \log N h≈logN
也就是意味着红黑树增删查改最坏也就是走最长路径 2 ⋅ log N 2\cdot \log N 2⋅logN,那么时间复杂度还是 O ( log N ) O(\log N) O(logN)。
二、红黑树的基本操作
1. 基本结构
红黑树本质上也是一棵自平衡二叉搜索树,其结点存的是一个三叉链,也就是说其不仅要存储左右子树的根结点,还要存储其父结点,以及每个结点的颜色(这里用枚举 e n u m enum enum 结构来存储所有可能的颜色)。
// 枚举值表示颜色
enum color
{red,black
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv; // 每个结点存储的值RBTreeNode<K, V>* _left; // 左子树RBTreeNode<K, V>* _right; // 右子树RBTreeNode<K, V>* _parent; // 父结点color _col; // 每个结点的颜色RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(red){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> node;
public:// ...
private:node* _root = nullptr;
};
2. 插入操作
由于红黑树的本质是一棵自平衡二叉搜索树,因此插入一个值可以按二叉搜索树规则进行插入:
bool insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new node(kv);_root->_col = black;return true;}node* parent = nullptr;node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 维持平衡操作// ..._root->_col = black;return true;
}
2.1 插入的过程
说明:下面我们假设把新增结点标识为 c c c( c u r cur cur), c c c 的父亲标识为 p p p( p a r e n t parent parent), p p p 的父亲标识为 g g g( g r a n d f a t h e r grandfather grandfather), p p p 的兄弟标识为 u u u( u n c l e uncle uncle)。

为了维持整棵树的平衡,插入后我们需要观察是否符合红黑树的 4 4 4 条规则:
-
如果是空树插入,新增结点必须是黑色结点(根)。如果是非空树插入,新增结点必须是红色结点,因为非空树插入,新增黑色结点就破坏了【规则 4 4 4】,【规则 4 4 4】是很难维护的。
-
如果插入后父亲结点是黑色的,则没有违反任何规则,插入结束。
-
如果插入后父亲结点是红色的,则违反【规则 3 3 3】。进一步分析, c c c 是红色, p p p 为红色, g g g 必为黑色,这三个颜色都固定了,关键的变化看 u u u 的情况,需要根据 u u u 分为以下两种情况分别处理:
黑 黑 黑 黑 / \ / \ / \ / \ 红 u 红 u u 红 u 红 / \ / \
红 红 红 红
2.2 情况一:变色
情况 1 1 1: u u u 存在且为红色,则只变色,不旋转。所以无论 c c c 是 p p p 的左还是右, p p p 是 g g g 的左还是右,都是下面的变色处理方式:
g g g g / \ / \ / \ / \ p u p u u p u p / \ / \
c c c c

| 状态 | c c c | p p p | g g g | u u u |
|---|---|---|---|---|
| 变色前 | 红色 | 红色 | 黑色 | 红色 |
| 变色后 | 红色 | 黑色 | 红色 | 黑色 |
变色前:
黑 黑 黑 黑 / \ / \ / \ / \ 红 红 红 红 红 红 红 红 / \ / \
红 红 红 红
变色后:
红 红 红 红 / \ / \ / \ / \ 黑 黑 黑 黑 黑 黑 黑 黑 / \ / \
红 红 红 红
【分析】 c c c 为红色, p p p 为红色, g g g 为黑色, u u u 存在且为红色,则将 p p p 和 u u u 变黑, g g g 变红。再把 g g g 当做新的 c c c,继续往上更新。
也就相当于:
-
保持 g g g 所在子树的黑色结点的数量不变(满足【规则 4 4 4】)
-
同时解决了 c c c 和 p p p 连续红色结点的问题(满足【规则 3 3 3】)
需要继续往上更新是因为: g g g 是红色
-
如果 g g g 的父亲还是红色,那么就还需要继续处理:
 图 2 2 2
图 2 2 2 -
如果 g g g 的父亲是黑色,则处理结束了。
-
如果 g g g 就是整棵树的根,再把 g g g 变回黑色。
跟 A V L AVL AVL 树类似,图 1 1 1 我们展示了一种具体情况,但是实际中需要这样处理的有很多种情况:
图 3 3 3 将以上类似的处理进行了抽象表达, d / e / f d/e/f d/e/f 代表每条路径拥有 b h bh bh( b h ≥ 0 bh\ge0 bh≥0)个黑色结点的子树, a / b a/b a/b 代表每条路径拥有 b h − 1 bh-1 bh−1 个黑色结点的根为红色的子树。

上述情况代表了所有只变色(情况一)的场景,因此一般来说我们只需要看抽象图即可,但通过下面根据 d / e / f d/e/f d/e/f 子树每条路径黑色结点的个数 b h bh bh 而分为的很多种具体场景,可以更直观的帮助我们理解抽象场景:
【第一种场景】 d / e / f d/e/f d/e/f 子树没有黑色结点( b h = 0 bh=0 bh=0):
即 a / b / d / e / f a/b/d/e/f a/b/d/e/f 都为空树, c c c 为新增结点。
注意: x x x 是 6 6 6 和 15 15 15 结点的任意一个孩子,都会引发这里的变色逻辑。

【第二种场景】 d / e / f d/e/f d/e/f 子树每条路径都只有 1 1 1 个黑色结点( b h = 1 bh=1 bh=1):
即 d / e / f d/e/f d/e/f 都代表一个 b h = 1 bh=1 bh=1 的红黑树:

-
c c c 之前是黑色结点,在 a a a 和 b b b 中插入引发 c c c 变色为红色结点。
-
d / e / f d/e/f d/e/f 为 x / y / z / m x/y/z/m x/y/z/m 中任意一种,组合为 4 × 4 × 4 4\times4\times4 4×4×4 种。
-
a a a 和 b b b 为红色结点,再 a a a 和 b b b 的四个孩子的任意位置插入,都会让 a a a 和 b b b 变成黑色, c c c 变成红色,继续向上更新,插入位置有 4 4 4 个位置。
-
所有情况组合起来合计: 4 × 4 × 4 × 4 = 256 4\times4\times4\times4=256 4×4×4×4=256 种。

【第三种场景】 d / e / f d/e/f d/e/f 子树每条路径都只有 2 2 2 个黑色结点( b h = 2 bh=2 bh=2):
即 d / e / f d/e/f d/e/f 都代表一个 b h = 2 bh=2 bh=2 的红黑树:


a a a 和 b b b 都代表一个 b h = 1 bh=1 bh=1 的根为红色的树:

-
d / e / f d/e/f d/e/f 的组合为: ( 256 + 16 ) × ( 256 + 16 ) × ( 256 + 16 ) = 20123648 (256+16)\times(256+16)\times(256+16)=20123648 (256+16)×(256+16)×(256+16)=20123648 种。
-
a a a 和 b b b 为根结点为红色的 b h = 1 bh=1 bh=1 的树,这里可以看到 a a a 和 b b b 的插入组合也不少: 16 × 16 = 256 16\times16=256 16×16=256 种。
-
a a a 或者 b b b 插入至少要经历两次变色和向上处理才能得到这里的情况,因此这里的组合情况至少是百亿种以上了: 20123648 × 256 × n ( n ≥ 2 ) ≥ 10303307776 20123648\times256\times n(n\ge2)\ge10303307776 20123648×256×n(n≥2)≥10303307776 种。

2.2 情况二:旋转+变色
情况 2 2 2: u u u 不存在或者 u u u 存在且为黑色,则需要先旋转,再变色。
旋转的核心逻辑和之前 A V L AVL AVL 树一模一样,可以参考我的这篇博客:【数据结构】 A V L AVL AVL 树。
不同的是,红黑树的旋转不用更新平衡因子:
- 左单旋:
void rotateL(node* parent)
{node* subR = parent->_right;node* subRL = subR->_left;node* pParent = parent->_parent;// 旋转核心逻辑subR->_left = parent;parent->_right = subRL;if (pParent == nullptr) // parent == _root_root = subR;else if (pParent->_left == parent)pParent->_left = subR;elsepParent->_right = subR;// 处理_parentif(subRL)subRL->_parent = parent;parent->_parent = subR;subR->_parent = pParent;
}
- 右单旋:
void rotateR(node* parent)
{node* subL = parent->_left;node* subLR = subL->_right;node* pParent = parent->_parent;// 旋转核心逻辑subL->_right = parent;parent->_left = subLR;if (pParent == nullptr) // parent == _root_root = subL;else if (pParent->_left = parent)pParent->_left = subL;elsepParent->_right = subL;// 处理_parentif (subLR)subLR->_parent = parent;parent->_parent = subL;subL->_parent = pParent;
}
(1) 单旋+变色
u u u 不存在,则 c c c 一定是新增结点。

u u u 存在且为黑,则 c c c 一定不是新增, c c c 之前是黑色的,是在 c c c 的子树中插入,符合情况 1 1 1,变色将 c c c 从黑色变成红色,更新上来的。

分析: p p p 必须变黑,才能解决连续红色结点的问题, u u u 不存在或者是黑色的,这里单纯的变色无法解决问题,因此需要旋转 + + + 变色。
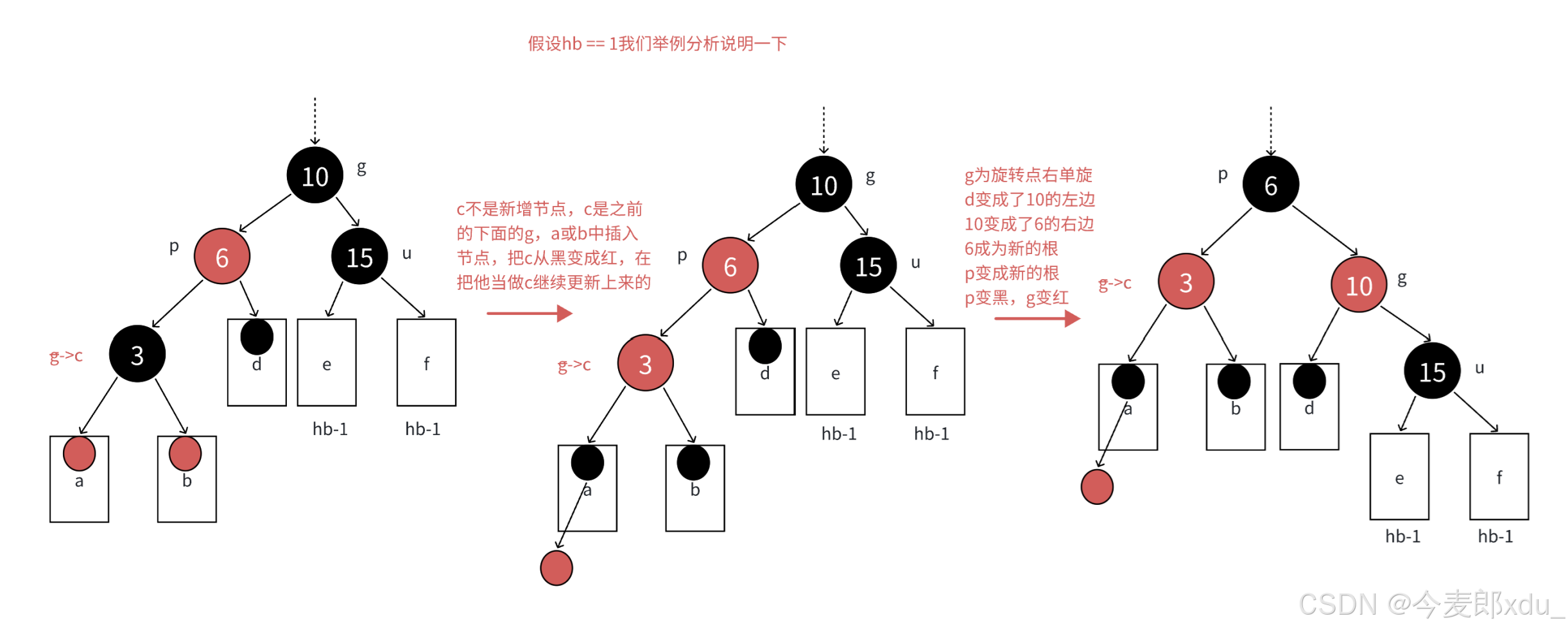
- 如果 p p p 是 g g g 的左, c c c 是 p p p 的左,那么以 g g g 为旋转点进行右单旋,再把 p p p 变黑, g g g 变红, p p p 变成这棵树新的根:
g p/ \ / \p u 右单旋-> c g/ \
c u 黑 红 黑 / \ / \ / \红 黑 右单旋-> 红 黑 变色-> 红 红 / \ \
红 黑 黑
这样子树黑色结点的数量不变【规则 3 3 3】,且没有连续的红色结点了【规则 4 4 4】,因此不需要往上更新,因为 p p p 的父亲是黑色还是红色或者为空都不违反规则。
if(parent == grandparent->_left)
{if(uncle == nullptr || uncle->_col = black){if(cur == parent->_left){// 右单旋rotateR(grandparent);// 变色parent->_col = black;grandparent->_col = red;}break;}
}
- 如果 p p p 是 g g g 的右, c c c 是 p p p 的右,那么以 g g g 为旋转点进行左单旋,再把 p p p 变黑, g g g 变红, p p p 变成这棵树新的根:
g p/ \ / \u p 左单旋-> g c\ / c u 黑 红 黑 / \ / \ / \黑 红 左单旋-> 黑 红 变色-> 红 红 \ / / 红 黑 黑
这样子树黑色结点的数量不变【规则 3 3 3】,且没有连续的红色结点了【规则 4 4 4】,因此不需要往上更新,因为 p p p 的父亲是黑色还是红色或者为空都不违反规则。
if(parent == grandparent->_right)
{if(uncle == nullptr || uncle->_col = black){if(cur == parent->_right){// 右单旋rotateR(grandparent);// 变色parent->_col = black;grandparent->_col = red; }break;}
}
(2) 双旋+变色
u u u 不存在,则 c c c 一定是新增结点。

u u u 存在且为黑,则 c c c 一定不是新增, c c c 之前是黑色的,是在 c c c 的子树中插入,符合情况 1 1 1,变色将 c c c 从黑色变成红色,更新上来的。

分析: p p p 必须变黑,才能解决连续红色结点的问题, u u u 不存在或者是黑色的,这里单纯的变色无法解决问题,因此需要旋转 + + + 变色。

- 如果 p p p 是 g g g 的左, c c c 是 p p p 的左,那么再以 p p p 为旋转点进行左单旋,再以 g g g 为旋转点进行右单旋,再把 c c c 变黑, g g g 变红, c c c 变成这棵树新的根:
g g c/ \ / \ / \p u 左单旋-> c u 右单旋-> p g \ / \c p u黑 黑 红 黑/ \ / \ / \ / \红 黑 左单旋-> 红 黑 右单旋-> 红 黑 变色-> 红 红 \ / \ \红 红 黑 黑
这样子树黑色结点的数量不变【规则 3 3 3】,且没有连续的红色结点了【规则 4 4 4】,因此不需要往上更新,因为 c c c 的父亲是黑色还是红色或者为空都不违反规则。
if(parent == grandparent->_left)
{if(uncle == nullptr || uncle->_col == black){if(cur == parent->_right){// 先左旋,再右旋rotateL(parent);rotateR(grandparent);// 变色cur->_col = black;grandparent->_col = red;}break;}
}
- 如果 p p p 是 g g g 的右, c c c 是 p p p 的右,那么先以 p p p 为旋转点进行右单旋,再以 g g g 为旋转点进行左单旋,再把 c c c 变黑, g g g 变红, c c c 变成这棵树新的根:
g g c/ \ / \ / \u p 右单旋-> u c 左单旋-> g p / \ / c p u 黑 黑 红 黑/ \ / \ / \ / \黑 红 右单旋-> 黑 红 左单旋-> 黑 红 变色-> 红 红 / \ / /红 红 黑 黑
这样子树黑色结点的数量不变【规则 3 3 3】,且没有连续的红色结点了【规则 4 4 4】,因此不需要往上更新,因为 c c c 的父亲是黑色还是红色或者为空都不违反规则。
if(parent == grandparent->_right)
{if(uncle == nullptr || uncle->_col == black){if(cur == parent->_left){// 先右旋,再左旋rotateR(parent);rotateL(grandparent);// 变色cur->_col = black;grandparent->_col = red;}break;}
}
3. 查找操作
红黑树的本质也是一棵自平衡的二叉搜索树,所以查找操作和二叉搜索树的操作完全一致,因此直接使用二叉搜索树逻辑实现即可,搜索效率为 O ( log N ) O(\log N) O(logN)。
node* find(const K& key)
{node* cur = _root;while (cur){if (key < cur->_kv.first){cur = cur->_left;}else if (key > cur->_kv.first){cur = cur->_right;}else{return cur;}}return nullptr;
}
4. 验证操作
这里直接获取最长路径和最短路径,检查最长路径不超过最短路径的 2 2 2 倍是不可行的,因为就算满足这个条件,红黑树也可能颜色不满足规则,当前暂时没出问题,后续继续插入还是会出问题的。所以我们还是去检查 4 4 4 点规则,满足这 4 4 4 点规则,就一定能保证最长路径不超过最短路径的 2 2 2 倍。

检查【规则 1 1 1】:枚举颜色类型,天然实现保证了颜色不是黑色就是红色。
检查【规则 2 2 2】:直接检查根即可。
检查【规则 3 3 3】:前序遍历检查,遇到红色结点查孩子不太方便,因为孩子有两个,且不一定存在,反过来检查父亲的颜色就方便多了。
检查【规则 4 4 4】:前序遍历,遍历过程中用形参记录跟到当前结点的 b l a c k N u m blackNum blackNum(黑色结点数量),前序遍历遇到黑色结点就 ++ b l a c k N u m blackNum blackNum,走到空就计算出了一条路径的黑色结点数量。再以任意一条路径黑色结点数量作为参考值,依次比较即可。
- 递归检查是否满足规则:
bool check(node* root, int blackNum, const int refNum){if (root == nullptr){if (blackNum != refNum){cout << "存在黑色结点不相等的路径!" << endl;return false;}return true;}if (root->_col == red && root->_parent->_col == red){cout << "存在有连续两个红色结点的路径!" << endl;return false;}if (root->_col == black){++blackNum;}return check(root->_left, blackNum, refNum) && check(root->_right, blackNum, refNum);}
- 检查是否平衡(为红黑树):
bool isBalance(){if (_root == nullptr)return true;if (_root->_col == red)return false;int refNum = 0;node* cur = _root;while (cur){if (cur->_col == black)++refNum;cur = cur->_left;}return check(_root, 0, refNum);}
三、红黑树的实现
由于这个数据结构是用 C C C++ 代码来模拟实现的,因此采用了模板来定义的红黑树类,所以不能将声明和定义分离,因此这里分为了两个文件: R B T r e e . h RBTree.h RBTree.h 来模拟实现并封装一个红黑树的模板类, t e s t . c p p test.cpp test.cpp 用来测试。
原理部分已经交代清楚了,这里给出完整代码:
- R B T r e e . h RBTree.h RBTree.h:
#pragma once
#include<iostream>using namespace std;// 枚举值表示颜色
enum color
{red,black
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv; // 每个结点存储的值RBTreeNode<K, V>* _left; // 左子树RBTreeNode<K, V>* _right; // 右子树RBTreeNode<K, V>* _parent; // 父结点color _col; // 每个结点的颜色RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(red){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> node;
public:void rotateL(node* parent){node* subR = parent->_right;node* subRL = subR->_left;node* pParent = parent->_parent;// 旋转核心逻辑subR->_left = parent;parent->_right = subRL;if (pParent == nullptr) // parent == _root_root = subR;else if (pParent->_left == parent)pParent->_left = subR;elsepParent->_right = subR;// 处理_parentif(subRL)subRL->_parent = parent;parent->_parent = subR;subR->_parent = pParent;}void rotateR(node* parent){node* subL = parent->_left;node* subLR = subL->_right;node* pParent = parent->_parent;// 旋转核心逻辑subL->_right = parent;parent->_left = subLR;if (pParent == nullptr) // parent == _root_root = subL;else if (pParent->_left = parent)pParent->_left = subL;elsepParent->_right = subL;// 处理_parentif (subLR)subLR->_parent = parent;parent->_parent = subL;subL->_parent = pParent;}bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new node(kv);_root->_col = black;return true;}node* parent = nullptr;node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 维持平衡操作while (parent && parent->_col == red) // 如果父亲是红,说明出现了连续的红色结点{node* grandparent = parent->_parent;if(parent == grandparent->_left){node* uncle = grandparent->_right;/*g/ \p u*/if (uncle && uncle->_col == red) // 情况一:u 存在且为红色{// 变色grandparent->_col = red;parent->_col = uncle->_col = black; // 继续向上更新cur = grandparent;parent = cur->_parent;}else // 情况二:u 存在且为黑色 或者 u 不存在{// 旋转 + 变色if (cur == parent->_left){/* 1. 单旋g p/ \ / \p u -> c g/ \c u*/rotateR(grandparent);// 变色parent->_col = black;grandparent->_col = red;}else{/* 2. 双旋g c/ \ / \p u -> p g\ \c u*/rotateL(parent);rotateR(grandparent);// 变色cur->_col = black;grandparent->_col = red;}break;}}else{node* uncle = grandparent->_left;/*g/ \u p*/if (uncle && uncle->_col == red) // 情况一:u 存在且为红色{// 只变色grandparent->_col = red;uncle->_col = parent->_col = black;// 继续向上更新cur = grandparent;parent = cur->_parent;}else // 情况二:u 存在且为黑色 或者 u 不存在{// 旋转 + 变色if (cur == parent->_right){/* 1. 单旋g p/ \ / \u p -> g c\ /c u*/rotateL(grandparent);// 变色parent->_col = black;grandparent->_col = red;}else{/* 2. 双旋g c/ \ / \u p -> g p/ /c u*/rotateR(parent);rotateL(grandparent);// 变色cur->_col = black;grandparent->_col = red;}break;}}}_root->_col = black;return true;}node* find(const K& key){node* cur = _root;while (cur){if (key < cur->_kv.first){cur = cur->_left;}else if (key > cur->_kv.first){cur = cur->_right;}else{return cur;}}return nullptr;}void inorder(){_inorder(_root);cout << endl;}int size(){return _size(_root);}int height(){return _height(_root);}bool isBalance(){if (_root == nullptr)return true;if (_root->_col == red)return false;int refNum = 0;node* cur = _root;while (cur){if (cur->_col == black)++refNum;cur = cur->_left;}return check(_root, 0, refNum);}
private:bool check(node* root, int blackNum, const int refNum){if (root == nullptr){if (blackNum != refNum){cout << "存在黑色结点不相等的路径!" << endl;return false;}return true;}if (root->_col == red && root->_parent->_col == red){cout << "存在有连续两个红色结点的路径!" << endl;return false;}if (root->_col == black){++blackNum;}return check(root->_left, blackNum, refNum) && check(root->_right, blackNum, refNum);}int _height(node* root){if (root == nullptr)return 0;int lh = _height(root->_left);int rh = _height(root->_right);return lh > rh ? lh + 1 : rh + 1;}int _size(node* root){if (root == nullptr)return 0;return _size(root->_left) + _size(root->_right) + 1;}void _inorder(node* root){if (root == nullptr)return;_inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_inorder(root->_right);}node* _root = nullptr;
};
- t e s t . c p p test.cpp test.cpp:
#include"RBTree.h"void test()
{RBTree<int, int> rbt;rbt.insert({ 1,1 });rbt.insert({ 2,2 });rbt.insert({ 3,3 });rbt.insert({ 4,4 });rbt.inorder();cout << "结点个数:" << rbt.size() << " 个" << endl;cout << "树的高度:" << rbt.height() << " 层" << endl;cout << "是否平衡:";rbt.isBalance() == true ? cout << "平衡!" << endl : cout << "不平衡:" << endl;
}int main()
{test();return 0;
}
总结
与 A V L AVL AVL 树相同,红黑树也是一种自平衡的二叉搜索树,通过给每个结点染色(红色或黑色),从而能够使用规则来约束树的结构,使整棵树近似平衡。
红黑树虽然平衡效果略逊于 A V L AVL AVL 树,但是红黑树的效率要比 A V L AVL AVL 树高,因为 A V L AVL AVL 树是通过高度差实现自平衡效果,几乎每几次插入或删除就需要旋转,而红黑树通过颜色规则约束整棵树,大部分情况直接变色就可以解决问题,需要旋转的次数大大降低,因此效率也就增加了。
C C C++ 的 S T L STL STL 标准库中, m a p map map 和 s e t set set 容器的底层结构使用的数据结构就是红黑树,可见红黑树的重要性和使用广泛。
相关文章:

【数据结构】红黑树
红黑树( R e d B l a c k T r e e Red\ Black\ Tree Red Black Tree)是一种自平衡二叉搜索树,也可以看作一种特化的 A V L AVL AVL 树(通过颜色规则来实现自平衡功能),都是在进行插入和删除操作时通过特定…...

ThreadLocal - 原理与应用场景详解
ThreadLocal 的基础概念 在 Java 的多线程世界里,线程之间的数据共享与隔离一直是一个关键话题。如果处理不当,很容易引发线程安全问题,比如数据混乱、脏读等。而 ThreadLocal 这个工具类,就像是为线程量身定制的 “私人储物柜”…...
)
VS Code 远程连接服务器:Anaconda 环境与 Python/Jupyter 运行全指南。研0大模型学习(第六、第七天)
VS Code 远程连接服务器:Anaconda 环境与 Python/Jupyter 运行全指南 在使用 VS Code 通过 SSH 远程连接到服务器进行开发时,尤其是在进行深度学习等需要特定环境的工作时,正确配置和使用 Anaconda 环境以及理解不同的代码运行方式非常关键。…...

chili3d调试6 添加左侧面板
注释前 一个一个注释看对应哪个窗口 无事发生 子方法不是显示的窗口 注释掉看看 没了 注释这个看看 零件页面没了 这个浏览器居然完全不用关的,刷新就重载了 注释看看 无工具栏版本 sidebar: 往框框里面加入 div({ className: style.input }, user_…...

Python变量全解析:从基础到高级的命名规则与数据类型指南
一、变量基础与内存机制 1.1 变量的三元构成 每个Python变量由三个核心要素构成: 标识(Identity):对象的内存地址,通过id(obj)获取(如id(name)输出0x5a1b2c3d)类型(Type&am…...

组装一台intel n95纯Linux Server服务器
前言 笔者自己的电脑是macmini m4,平时都是使用虚拟机来充当Linux服务器(系统Ubuntu Server),但是毕竟是ARM CPU,而且黄金内存,开不了几个虚拟机(加内存不划算),所以组装…...

计算机网络中的网络层:架构、功能与重要性
一、网络层概述 在计算机网络的分层模型中,网络层(Network Layer)位于 数据链路层 之上,传输层 之下。网络层的主要任务是处理数据包的路由选择、转发以及分段,使得信息能够从源设备传送到目标设备。它还通过 IP协议&…...
:NLP中放弃使用循环神经网络架构)
Transformer系列(一):NLP中放弃使用循环神经网络架构
NLP中放弃使用循环神经网络架构 一、符号表示与概念基础二、循环神经网络1. 依赖序列索引存在的并行计算问题2. 线性交互距离 三、总结 该系列笔记阐述了自然语言处理(NLP)中不再采用循环架构(recurrent architectures)的原因&…...
Linux 库制作与原理)
(学习总结34)Linux 库制作与原理
Linux 库制作与原理 库的概念静态库操作归档文件命令 ar静态库制作静态库使用 动态库动态库制作动态库使用与运行搜索路径问题解决方案方案2:建立同名软链接方案3:使用环境变量 LD_LIBRARY_PATH方案4:ldconfig 方案 使用外部库目标文件ELF 文…...

【QT】 QT中的列表框-横向列表框-树状列表框-表格列表框
QT中的列表框-横向列表框-树状列表框-表格列表框 1.横向列表框(1)主要方法(2)信号(3) 示例代码1:(4) 现象:(5) 示例代码2:加载目录项在横向列表框显示(6) 现象: 2.树状列表框 QTreeWidget(1)使用思路(2)信号(3)常用的接口函数(4) 示例代码&am…...

使用DeepSeek的AIGC的内容创作者,如何看待陈望道先生所著的《修辞学发凡》?
目录 1.从修辞手法的运用角度 2.从语言风格的塑造角度 3.从提高创作效率角度 4.从文化传承与创新角度 大家好这里是AIWritePaper官方账号,官网👉AIWritePaper~ 《修辞学发凡》是陈望道 1932 年出版的中国第一部系统的修辞学著作,科学地总…...
的自动化跨平台打包)
使用 GitHub Actions 和 Nuitka 实现 Python 应用(customtkinter ui库)的自动化跨平台打包
目录 引言前置准备配置文件详解实现细节CustomTkinter 打包注意事项完整配置示例常见问题 引言 在 Python 应用开发中,将源代码打包成可执行文件是一个常见需求。本文将详细介绍如何使用 GitHub Actions 和 Nuitka 实现自动化的跨平台打包流程,支持 W…...

【Part 2安卓原生360°VR播放器开发实战】第一节|通过传感器实现VR的3DOF效果
《VR 360全景视频开发》专栏 将带你深入探索从全景视频制作到Unity眼镜端应用开发的全流程技术。专栏内容涵盖安卓原生VR播放器开发、Unity VR视频渲染与手势交互、360全景视频制作与优化,以及高分辨率视频性能优化等实战技巧。 📝 希望通过这个专栏&am…...

【1】云原生,kubernetes 与 Docker 的关系
Kubernetes?K8s? Kubernetes经常被写作K8s。其中的数字8替代了K和s中的8个字母——这一点倒是方便了发推,也方便了像我这样懒惰的人。 什么是云原生? 云原生: 它是一种构建和运行应用程序的方法,它包含&am…...

基于Redis实现RAG架构的技术解析与实践指南
一、Redis在RAG架构中的核心作用 1.1 Redis作为向量数据库的独特优势 Redis在RAG架构中扮演着向量数据库的核心角色,其技术特性完美契合RAG需求: 特性技术实现RAG应用价值高性能内存存储基于内存的键值存储架构支持每秒百万级的向量检索请求分布式架构…...

trivy开源安全漏洞扫描器——筑梦之路
开源地址:https://github.com/aquasecurity/trivy.git 可扫描的对象 容器镜像文件系统Git存储库(远程)虚拟机镜像Kubernetes 在容器镜像安全方面使用广泛,其他使用相对较少。 能够发现的问题 正在使用的操作系统包和软件依赖项…...

pnpm确认全局下载安装了还是显示cnpm不是内部或外部命令,也不是可运行的程序
刚开始是正常使用的。突然开始用不了了一直报错 1.在确保自己node和npm都一直正常使用并且全局安装pnpm的情况下 打开cmd查看npm的环境所在位置 npm config get prefix 2.接着打开高级系统设置 查看自己的path配置有没有问题 确认下载了之后pnpm -v还报错说明没有查询到位置 …...

基于 pnpm + Monorepo + Turbo + 无界微前端 + Vite 的企业级前端工程实践
基于 pnpm Monorepo Turbo 无界微前端 Vite 的企业级前端工程实践 一、技术演进:为什么引入 Vite? 在微前端与 Monorepo 架构落地后,构建性能成为新的优化重点: Webpack 构建瓶颈:复杂配置导致开发启动慢&#…...

软考高级系统架构设计师-第15章 知识产权与标准化
【本章学习建议】 根据考试大纲,本章主要考查系统架构设计师单选题,预计考3分左右,较为简单。 15.1 标准化基础知识 1. 标准的分类 分类 内容 国际标准(IS) 国际标准化组织(ISO)、国际电工…...

MySQL 视图
核心目标: 学习如何创建和使用视图,以简化复杂的查询、提供数据访问控制、实现逻辑数据独立性,并通过 WITH CHECK OPTION 保证数据一致性。 什么是视图? 视图(View)是一种虚拟表,其内容由一个 …...

[操作系统] 信号
信号 vs IPC 板书最后提到了 “信号 vs IPC”,暗示了信号也是一种进程间通信 (Inter-Process Communication, IPC) 的机制。虽然信号的主要目的是事件通知,但它也可以携带少量的信息(即信号的类型)。 初探“信号”——操作系统的“…...
)
网络基础(协议,地址,OSI模型、Socket编程......)
目录 一、计算机网络发展 二、协议 1.认识协议 2.OSI七层模型 3.TCP/IP 五层(或四层)模型 4.协议本质 三、网络传输流程 1.MAC地址 2.协议栈 3.IP地址 IP地址 vs MAC地址 1. 核心区别 2. 具体通信过程类比 3. 关键总结 为什么需要两者? 4.协议栈图解…...

产品经理学习过程
一:扫盲篇(初始产品经理) 阶段1:了解产品经理 了解产品经理是做什么的、产品经理的分类、产品经理在实际工作中都会接触什么样的岗位、以及产品经理在实际工作中具体要做什么事情。 二:准备篇 阶段2:工…...

深入理解Java包装类:自动装箱拆箱与缓存池机制
深入理解Java包装类:自动装箱拆箱与缓存池机制 对象包装器 Java中的数据类型可以分为两类:基本类型和引用类型。作为一门面向对象编程语言, 一切皆对象是Java语言的设计理念之一。但基本类型不是对象,无法直接参与面向对象操作&…...

Linux中的信号量
目录 信号量概念 定义 操作 类型 应用 信号量封装 一、创建信号量 头文件 函数原型 参数说明 返回值 示例 二、设置信号量初始值 头文件 函数原型 参数解释 返回值 示例 三、信号量的P操作 头文件 函数原型 参数解释 返回值 示例 四、信号量的V操作 示…...

深入理解linux操作系统---第15讲 Web 服务器 Nginx
15.1 Nginx 概述 核心特性与历史背景 Nginx由俄罗斯工程师Igor Sysoev于2002年开发,2004年正式发布,旨在解决传统服务器(如Apache)的C10K问题(即单机万级并发连接处理)。其采用事件驱动(Event…...

深度解析算法之前缀和
25.【模版】一维前缀和 题目链接 描述 输入描述 输出描述 输出q行,每行代表一次查询的结果. 示例 输入: 3 2 1 2 4 1 2 2 3 复制 输出: 3 6 这个题的话就是下面的样子,我们第一行输入 3 2的意思即是这个数组是3个元素大小的数组&…...

混合精度训练中的算力浪费分析:FP16/FP8/BF16的隐藏成本
在大模型训练场景中,混合精度训练已成为降低显存占用的标准方案。然而,通过NVIDIA Nsight Compute深度剖析发现,精度转换的隐藏成本可能使理论算力利用率下降40%以上。本文基于真实硬件测试数据,揭示不同精度格式的计算陷阱。…...

6.8 Python定时任务实战:APScheduler+Cron实现每日/每周自动化调度
Python定时任务实战:APScheduler+Cron实现每日/每周自动化调度 实现每日和每周定时任务 关键词:定时任务调度、Python 原生调度器、Cron 脚本、异常重试机制、任务队列管理 1. 定时任务架构设计 采用 分层调度架构 实现灵活的任务管理: #mermaid-svg-PnZcDOgOklVieQ8X {f…...

[Android] 豆包爱学v4.5.0小学到研究生 题目Ai解析
[Android] 豆包爱学 链接:https://pan.xunlei.com/s/VOODT6IclGPsC7leCzDFz521A1?pwdjxd8# 拍照解析答案 【应用名称】豆包爱学 【应用版本】4.5.0 【软件大小】95mb 【适用平台】安卓 【应用简介】豆包爱学,一般又称河马爱学教育平台app,河马爱学。 关…...

swift-12-Error处理、关联类型、assert、泛型_
一、错误类型 开发过程常见的错误 语法错误(编译报错) 逻辑错误 运行时错误(可能会导致闪退,一般也叫做异常) 2.1 通过结构体 第一步 struct MyError : Errort { var msg: String } 第二步 func divide(_ …...
20250409 - 20250419)
每日定投40刀BTC(14)20250409 - 20250419
定投 坚持 《磨剑篇》浮生多坎壈,志业久盘桓。松柏凌霜易,骅骝涉险难。砺锋临刃缺,淬火取金残。但使精魂在,重开万象端。...
)
【刷题Day20】TCP和UDP(浅)
TCP 和 UDP 有什么区别? TCP提供了可靠、面向连接的传输,适用于需要数据完整性和顺序的场景。 UDP提供了更轻量、面向报文的传输,适用于实时性要求高的场景。 特性TCPUDP连接方式面向连接无连接可靠性提供可靠性,保证数据按顺序…...

大数据建模与评估
文章目录 实战案例:电商用户分群与价值预测核心工具与库总结一、常见数据挖掘模型原理及应用(一)决策树模型(二)随机森林模型(三)支持向量机(SVM)模型(四)K - Means聚类模型(五)K - Nearest Neighbors(KNN)模型二、运用Python机器学习知识实现数据建模与评估(一…...

Python语法系列博客 · 第6期[特殊字符] 文件读写与文本处理基础
上一期小练习解答(第5期回顾) ✅ 练习1:字符串反转模块 string_tools.py # string_tools.py def reverse_string(s):return s[::-1]调用: import string_tools print(string_tools.reverse_string("Hello")) # 输出…...

Pandas取代Excel?
有人在知乎上提问:为什么大公司不用pandas取代excel? 而且列出了几个理由:Pandas功能比Excel强大,运行速度更快,Excel除了简单和可视化界面外,没有其他更多的优势。 有个可怕的现实是,对比Exce…...

《解锁图像“高清密码”:超分辨率重建之路》
在图像的世界里,高分辨率意味着更多细节、更清晰的画面,就像用高清望远镜眺望远方,一切都纤毫毕现。可现实中,我们常被低分辨率图像困扰,模糊的监控画面、老旧照片里难以辨认的面容……不过别担心,图像超分…...

杨校老师课堂之C++入门练习题梳理
采用C完成下列题目,要求每题目的时间限制:1秒 内存限制:128M 1. 交换个位与十位的数字 时间限制:1秒 内存限制:128M 题目描述 试编写一个程序,输入一个两位数,交换十位与个位上的数字并输出。 …...

基于springboot的老年医疗保健系统
博主介绍:java高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了六年的毕业设计程序开发,开发过上千套毕业设计程序,没有什么华丽的语言࿰…...

数据分析与挖掘
一 Python 基本语法 变量与数据类型 : Python 中变量无需声明,直接赋值即可。 常见的数据类型有数值型(整型 int、浮点型 float、复数型 complex)、字符串型(str,用单引号、双引号或三引号括起来ÿ…...

RoBoflow数据集的介绍
https://public.roboflow.com/object-detection(该数据集的网址) 可以看到一些基本情况 如果我们想要下载,直接点击 点击图像可以看到一些基本情况 可以点击红色箭头所指,右边是可供选择的一些yolo模型的格式 如果你想下载…...

大模型Rag - 两大检索技术
一、稀疏检索:关键词匹配的经典代表 稀疏检索是一种基于关键词统计的传统检索方法。其基本思想是:通过词频和文档频率来衡量一个文档与查询的相关性。 核心原理 文档和查询都被表示为稀疏向量(如词袋模型),只有在词…...

【T型三电平仿真】SVPWM调制
目录 仿真模型分析 克拉克变换 大扇区判断编辑 小区域判断 计算基本电压矢量作用时间 确定基本电压矢量的作用顺序 作用时间和矢量作用顺序对应 七段式化生成阶梯图 矢量状态分布 本人学习过程中提出的问题和解释 SVPWM调制实现了什么功能 SVPWM的算法步骤是什么…...

树莓派5-开发应用笔记
0.树莓派系统目录 /home:用户目录。 除了root用户外,其他所有的使用者的数据都存放在这个目录下,在树莓派的系统中,/home目录中有一个pi的子目录,这个就是pi用户的默认目录。 /bin: 主要放置系统的必备执行文件目录。 …...

[Java实战经验]异常处理最佳实践
一些好的异常处理实践。 目录 异常设计自定义异常为异常设计错误代码(状态码)设计粒度全局异常处理异常日志信息保留 异常处理时机资源管理try-with-resources异常中的事务 异常设计 自定义异常 自定义异常设计,如业务异常定义BusinessExce…...

AOSP的Doze模式-LightIdle初识
前言 从Android 6.0开始,谷歌引入了Doze模式(打盹模式)的省电技术延长电池使用时间。根据第三方测试显示,两台同样的Nexus 5,开启的Doze的一台待机能达到533小时,而未开启Doze的一台待机只能达到200小时。Doze省电效果十分明显。…...

QML动画--ParticleSystem
ParticleSystem 是 QML 中用于创建和管理粒子系统的组件,可以制作各种粒子效果如火焰、烟雾、爆炸等。 基本用法 qml import QtQuick.Particles 2.15ParticleSystem {id: particleSystemImageParticle {source: "particle.png"color: "red"a…...

Win 11 重装 Ubuntu 双系统方法
有时候 Ubuntu 环境崩溃了,或者版本过低,需要卸载重装。本文介绍重装的方法,默认已经有一个双系统。 1. 删除原先 Ubuntu 分区 首先打开 Win 的磁盘管理,找到 Ubuntu 的分区,右键删除分区(注意不要错删 wi…...

单例模式:懒汉式的两种优化写法
单例模式:全局唯一实例 懒汉式:获取时才初始化 ①静态局部变量实现(Meyer’s Singleton)【推荐】 /* 类内创建自身实例的可行性分析:在C中,类可以通过静态成员函数创建自身实例。这种机制的核心在于&…...

详细解释浏览器是如何渲染页面的?
渲染流程概述 渲染的目标:将HTML文本转化为可以看到的像素点 当浏览器的网络线程收到 HTML 文档后,会产生一个渲染任务,并将其传递给渲染主线程的消息队列。在事件循环机制的作用下,渲染主线程取出消息队列中的渲染任务࿰…...
