当前位置：首页 > news >正文

简单线段树的讲解（一点点的心得体会）

news 来源：原创 2025/8/10 23:05:23

一、初识线段树

图例：

编辑

数组存储：

指针存储：

理由：

build函数建树

二、线段树的区间修改维护

区间修改维护：

区间修改的操作：

递归更新过程：

区间修改update：

三、线段树的区间查询

区间查询：

区间查询的操作：

递归查询过程：

区间查询query：

例题：

完整代码：

数组实现：

指针实现：

总结

前言

今天我们来学习一下线段树

模板题目：P3372 【模板】线段树 1 - 洛谷

一、初识线段树

首先我们来了解一下什么是线段树

线段树是一种数据结构，通常用来解决区间查询的问题。它主要用于对一个包含有 n 个元素的数组进行区间操作，如查询某个区间内的最大值、最小值、区间和等。

线段树的基本思想是将整个数组按照一定规则进行分割，每个节点代表一个区间。每个节点保存区间内的信息，如最大值、最小值、区间和等。父节点的信息可以通过子节点的信息合并得到，这样就可以快速进行区间查询。

线段树通常是一棵完全二叉树，叶子节点对应于数组中的元素，每个非叶子节点表示了其区间的信息。对于一个包含 n 个元素的数组，线段树的节点数一般是 2n-1 或 2^k-1，其中 k 是大于等于 n 的最小整数。线段树的构建包括建树和更新两个主要操作，查询时可以通过递归的方式进行。

线段树在解决区间查询问题时效率很高，时间复杂度一般为 O(logn)，其中 n 是数组元素个数。因此，线段树被广泛应用于需要频繁进行区间查询的场景，如动态区间最值查询、区间和查询等。

我这次是联系模板题目P3372 【模板】线段树 1 - 洛谷讲解的最简单的类型

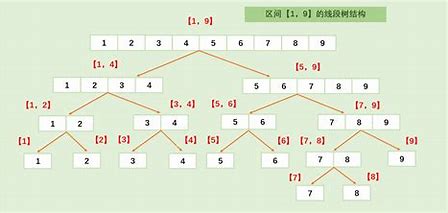
图例：

通过这幅图我们可以看出，线段树是根据不断的从子节点拿值，来更新父节点的值，直到得到整个区间的值，和分治的思想有点像，感觉

线段树的存储方式有两种常见的实现方法：数组存储和指针存储。

数组存储：
- 在数组存储中，线段树被表示为一个静态的完全二叉树。数组的下标从 1 开始，对于节点 i，其左子节点为 2i，右子节点为 2i+1。
- 如果线段树的叶子节点数量为 n，那么数组的大小一般取 4n，以确保足够的空间。
- 线段树根节点一般存储在数组下标为 1 的位置。
- 通过按照规则在数组中存储线段树的节点，可以方便地进行查询和更新操作。
指针存储：
- 在指针存储中，线段树被表示为一个动态的树结构，每个节点通过指针指向其左右子节点。
- 每个节点通常由一个包含左右子节点指针的结构体或类表示。
- 指针存储方式在构建线段树时会动态生成节点，相对于数组存储来说更加灵活，但可能会消耗更多的内存空间。

无论是数组存储还是指针存储，线段树的基本操作都是相似的，包括建树、查询和更新。选择适合具体应用场景的存储方式可以更好地利用线段树的优势，提高算法效率。

首先是数组存储，我们最先要知道的是数组的大小需要开多大，在线段树的数组存储中，通常会将数组的大小设置为 4n，其中 n 表示线段树的叶子节点数量。

理由：

完全二叉树性质：线段树一般是一棵完全二叉树，具有规律性的结构。在数组存储方式下，为了方便表示完全二叉树，需要保证数组的大小是某一层节点数量的上限。对于一棵深度为 k 的完全二叉树，叶子节点数量最多为 2^k，因此数组大小一般设置为 4 * 2^k，以确保足够的空间。
节点的父子关系：在数组存储方式中，节点 i 的左子节点一般存储在位置 2i，右子节点存储在位置 2i+1。设置数组大小为 4n 可以保证对于任意节点 i，其子节点在数组中的位置都是有效的，不会越界。
方便计算左右子树位置：在线段树的查询和更新操作中，经常需要根据节点的索引快速定位其左右子树节点。通过设置数组大小为 4n，可以方便地根据节点索引计算出其左右子节点的位置，简化操作。

然后开一个build函数建树，具体操作如下：

定义数组：首先，需要定义一个大小为 4n 的数组，其中 n 是线段树的叶子节点数量。这个数组将用于存储线段树的节点信息。
构建线段树：一般将线段树按照完全二叉树的形式存储在数组中。假设根节点在数组中的索引是 1，那么对于节点 i，其左子节点为 2i，右子节点为 2i + 1。
存储节点信息：每个节点需要保存代表的区间范围和相应的信息，比如区间的最大值、最小值、和等等。在数组中，可以按照某种顺序依次存储这些信息，以便后续的查询和更新操作。
建立线段树：通过递归或迭代的方式构建线段树。一般会从叶子节点开始向上构建，通过合并子节点的信息得到父节点的信息，直至构建完整的线段树。
查询和更新：通过线段树的结构和数组存储，可以实现高效的区间查询和更新操作。比如，对于查询一个区间的最大值，可以通过递归向下查询到包含目标区间的节点，并根据存储的信息计算出结果。
记得注意边界情况：在实现线段树时，需要考虑树的边界情况，比如树的根节点索引是 1，叶子节点索引从 n+1 开始等，以确保正确地访问和操作节点。

build函数建树

void build(LL l, LL r, LL fa) {if (l == r) // //如果左右区间相同，那么必然是叶子节，只有叶子节点是被真实赋值的{t[fa] = a[l];return;}LL mid = (l + r) >> 1;build( l, mid, fa << 1);build(mid + 1, r, fa << 1 | 1);
//使用二分来优化psuh_up(fa);//此处由于我们是要通过子节点来维护父节点，所以push_up的位置应当是在回溯时将子节点的值取和交给父节点
}

二、线段树的区间修改维护

线段树是一种用于解决区间查询和修改问题的数据结构。在线段树中，区间修改维护指的是在给定一个区间，并修改该区间内所有元素的操作。

区间修改维护：
- 当需要修改线段树中某个特定区间的值时，可以通过递归的方式向下更新区间。
- 如果要修改的区间与当前节点表示的区间没有交集，则无需修改该节点。
- 如果要修改的区间完全包含当前节点的区间，则直接更新当前节点的信息，并将修改操作下传给子节点。
- 如果要修改的区间与当前节点的区间部分相交，则需要先将当前节点的信息更新，然后将修改操作同时下传给左右子节点。
区间修改的操作：
- 区间修改的操作通常包括加法、减法、赋值等。
- 当需要对区间内的每个元素进行相同的修改时，可以利用线段树的特性进行高效操作。
- 在修改区间时，需要根据当前节点的区间范围、待修改区间和修改方式来确定如何操作当前节点和其子节点。
递归更新过程：
- 从线段树的根节点开始递归向下更新，直到找到包含待修改区间的叶子节点。
- 在递归过程中根据节点的区间范围和待修改区间的关系，决定如何更新节点的信息并向下传递修改操作。

此外，对于区间操作，我们考虑引入一个名叫“ lazy tag ”（懒标记）的东西——之所以称其“lazy”，是因为原本区间修改需要通过先改变叶子节点的值，然后不断地向上递归修改祖先节点直至到达根节点，时间复杂度最高可以到达 O(nlogn) 的级别。但当我们引入了懒标记之后，区间更新的期望复杂度就降到了 O(logn) 的级别且甚至会更低。

因此，我们再弄一个tag数组，大小也是4*N

区间修改update：

void psuh_up(LL fa) {t[fa] = t[fa << 1] + t[fa << 1 | 1];//向上不断维护父节点
}
void push_down(LL l,LL r,LL fa) {LL mid = (l + r) >> 1;t[fa << 1] += tag[fa] * (mid - l + 1);tag[fa << 1] += tag[fa];t[fa << 1|1] += tag[fa] * (r-mid);tag[fa << 1|1] += tag[fa];tag[fa] = 0;// //每次将懒惰标识下放到两个儿子节点，自身置为0，以此不断向下传递 
}
void update(LL ql, LL qr, LL l, LL r, LL k, LL fa) {if (ql <= l && qr >= r) //如果区间被包含，直接返回该节点的懒惰标识{t[fa] +=k * (r - l + 1);tag[fa] += k;return;}LL mid = (l + r) >> 1;push_down(l, r, fa);//下放懒惰标识if (ql <= mid)update(ql, qr, l, mid,k, fa << 1);//朝左边下放if (qr > mid)update(ql, qr, mid + 1, r,k, fa << 1 | 1);//右边psuh_up(fa);//再将修改后的值向上返回，维护父节点
}

三、线段树的区间查询

区间查询：
- 当需要查询线段树中某个特定区间的信息时，可以通过递归的方式向下查询区间。
- 如果要查询的区间与当前节点表示的区间没有交集，则无需查询该节点，直接返回默认值（如0或无穷大）。
- 如果要查询的区间完全包含当前节点的区间，则直接返回该节点存储的信息。
- 如果要查询的区间与当前节点的区间部分相交，则需要同时查询左右子节点，并根据查询结果合并得到最终结果。
区间查询的操作：
- 区间查询的操作通常包括求和、求最大值、求最小值等。
- 在查询区间时，需要根据当前节点的区间范围、待查询区间和查询方式来确定如何操作当前节点和其子节点。
递归查询过程：
- 从线段树的根节点开始递归向下查询，直到找到包含待查询区间的叶子节点。
- 在递归过程中根据节点的区间范围和待查询区间的关系，决定如何查询节点的信息并向下传递查询操作。
- 最终将所有查询结果合并得到最终的区间查询结果。

通过以上方法，可以实现对线段树中特定区间的查询操作。线段树区间查询是线段树的一个重要功能，能够快速有效地获取区间内的信息，提高了区间查询的效率。

区间查询query：

LL query(LL ql, LL qr, LL l, LL r, LL fa) {LL ret = 0;if (ql <= l && qr >= r) 如果区间被包含，直接返回该节点的懒惰标识{return t[fa];}LL mid = (l + r) >> 1;push_down(l, r, fa);//没有被包含，下放任务if (ql <= mid)ret += query(ql, qr, l, mid, fa << 1);if (qr > mid)ret += query(ql, qr, mid + 1, r, fa << 1|1);//在查询范围的左区间和右区间的值相加并返回return ret;
}

例题：

模板题目：P3372 【模板】线段树 1 - 洛谷

完整代码：

数组实现：

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL n, m, t[N * 4], tag[N * 4], a[N];
void psuh_up(LL fa) {t[fa] = t[fa << 1] + t[fa << 1 | 1];//向上不断维护父节点
}
void push_down(LL l,LL r,LL fa) {LL mid = (l + r) >> 1;t[fa << 1] += tag[fa] * (mid - l + 1);tag[fa << 1] += tag[fa];t[fa << 1|1] += tag[fa] * (r-mid);tag[fa << 1|1] += tag[fa];tag[fa] = 0;// //每次将懒惰标识下放到两个儿子节点，自身置为0，以此不断向下传递 
}
LL query(LL ql, LL qr, LL l, LL r, LL fa) {LL ret = 0;if (ql <= l && qr >= r) 如果区间被包含，直接返回该节点的懒惰标识{return t[fa];}LL mid = (l + r) >> 1;push_down(l, r, fa);//没有被包含，下放任务if (ql <= mid)ret += query(ql, qr, l, mid, fa << 1);if (qr > mid)ret += query(ql, qr, mid + 1, r, fa << 1|1);//在查询范围的左区间和右区间的值相加并返回return ret;
}
void update(LL ql, LL qr, LL l, LL r, LL k, LL fa) {if (ql <= l && qr >= r) //如果区间被包含，更新懒惰标识并返回{t[fa] +=k * (r - l + 1);tag[fa] += k;return;}LL mid = (l + r) >> 1;push_down(l, r, fa);//下放懒惰标识if (ql <= mid)update(ql, qr, l, mid,k, fa << 1);//朝左边下放if (qr > mid)update(ql, qr, mid + 1, r,k, fa << 1 | 1);//右边psuh_up(fa);//再将修改后的值向上返回，维护父节点
}
void build(LL l, LL r, LL fa) {if (l == r) // //如果左右区间相同，那么必然是叶子节，只有叶子节点是被真实赋值的{t[fa] = a[l];return;}LL mid = (l + r) >> 1;build(l, mid, fa << 1);build(mid + 1, r, fa << 1 | 1);//使用二分来优化psuh_up(fa);//此处由于我们是要通过子节点来维护父节点，所以push_up的位置应当是在回溯时将子节点的值取和交给父节点
}
int main() {cin >> n >> m;for (int i = 1; i <= n; i++)cin >> a[i];build(1, n, 1);while (m--) {int op; cin >> op;if (op == 1) {LL x, y, k; cin >> x >> y >> k;update(x, y, 1, n, k, 1);}else if(op==2){LL x, y;cin >> x >> y;cout << query(x, y, 1, n, 1) << endl;}}return 0;
}

指针实现：

#include <iostream>
#include <vector>using namespace std;struct Node {int start, end;int sum;Node *left, *right;Node(int start, int end) : start(start), end(end), sum(0), left(nullptr), right(nullptr) {}
};Node* buildSegmentTree(vector<int>& nums, int start, int end) {if (start > end) {return nullptr;}Node* root = new Node(start, end);if (start == end) {root->sum = nums[start];} else {int mid = start + (end - start) / 2;root->left = buildSegmentTree(nums, start, mid);root->right = buildSegmentTree(nums, mid + 1, end);root->sum = root->left->sum + root->right->sum;}return root;
}int query(Node* root, int qs, int qe) {if (root == nullptr || qs > root->end || qe < root->start) {return 0;} else if (qs <= root->start && qe >= root->end) {return root->sum;} else {return query(root->left, qs, qe) + query(root->right, qs, qe);}
}int main() {vector<int> nums = {1, 3, 5, 7, 9, 11};Node* root = buildSegmentTree(nums, 0, nums.size() - 1);cout << "Sum of elements in range [2, 4]: " << query(root, 2, 4) << endl;return 0;
}

总结

本文关于线段树的讲解就到这里，有什么疑问或者有什么错误的地方欢迎一起交流学习

简单线段树的讲解（一点点的心得体会）

目录一、初识线段树图例： 编辑数组存储： 指针存储： 理由： build函数建树二、线段树的区间修改维护区间修改维护： 区间修改的操作： 递归更新过程： 区间修改update&#xff1a…...

编程日记 2025/8/10 23:05:23

在 Node.js 中使用原生 `http` 模块，获取请求的各个部分：请求行、请求头、请求体、请求路径、查询字符串等内容

在 Node.js 中使用原生 http 模块，可以通过 req 对象来获取请求的各个部分：请求行、请求头、请求体、请求路径、查询字符串等内容。 ✅ 一、基础结构 const http require(http); const url require(url);const server http.createServer((req, res)…...

编程日记 2025/8/10 19:32:07

深度学习--mnist数据集实现卷积神经网络的手写数字识别

文章目录一、卷积神经网络CNN1、什么是CNN2、核心3、构造二、案例1、下载数据集（训练、测试集）并展示画布2、打包数据图片3、判断系统使用的是CPU还是GPU4、定义CNN神经网络5、训练和测试模型一、卷积神经网络CNN 1、什么是CNN 卷积神经网络是一种深…...

编程日记 2025/8/10 22:59:12

python基础知识点（1）

python语句一行写一条语句一行内写多行语句，使用分号分隔建议每行写一句，且结束时不写分号写在[ ]、{ }内的跨行语句，被视为一行语句\ 是续行符,实现分行书写功能反斜杠表示下一行和本行是同一行代码块与缩进代码块复合语句&#xf…...

编程日记 2025/8/10 4:50:38

详解反射型 XSS 的后续利用方式：从基础窃取到高级组合拳攻击链

在网络安全领域，反射型跨站脚本攻击（Reflected Cross-Site Scripting，简称反射型 XSS）因其短暂的生命周期和临时性，常被视为“低危”漏洞，威胁性不如存储型或 DOM 型 XSS。然而，这种看法低估了它…...

编程日记 2025/8/10 22:54:34

【问题笔记】解决python虚拟环境运行脚本无法激活问题

【问题笔记】解决python虚拟环境运行脚本无法激活问题错误提示问题所在解决方法**方法 1：临时更改执行策略****方法 2：永久更改执行策略** **完整流程示例** 错误提示 PS F:\PythonProject\0419graphrag-local-ollama-main> venv1\Scripts\activate…...

编程日记 2025/8/10 23:01:11

CF148D Bag of mice

题目传送门思路状态设计设 d p i , j dp_{i, j} dpi,j 表示袋中有 i i i 个白鼠和 j j j 个黑鼠时， A A A 能赢的概率。状态转移现在考虑抓鼠情况： A A A 抓到白鼠：直接判 A A A 赢，概率是 i i j \frac{i}{i j}…...

编程日记 2025/8/10 22:59:13

精益数据分析（6/126）：深入理解精益分析的核心要点

精益数据分析（6/126）：深入理解精益分析的核心要点在创业和数据驱动的时代浪潮中，我们都在不断探索如何更好地利用数据推动业务发展。我希望通过和大家分享对《精益数据分析》的学习心得，一起在这个充满挑战和机遇的领…...

编程日记 2025/8/10 22:57:07

package.json ^、~、＞、＞=、* 详解

package.json ^、~、>、>、* 详解在 Vue 项目中，package.json 文件的依赖项（dependencies）和开发依赖项（devDependencies）中，版本号前可能会带有一些特殊符号，例如 ^、~、>、<、&g…...

编程日记 2025/8/10 22:57:08

2025年赣教云智慧作业微课PPT模板

江西的老师们注意，2025年赣教云智慧作业微课PPT模版和往年不一样，千万不要搞错了，图上的才是正确的2025年的赣教云智慧作业微课PPT模版，赣教云智慧作业官网有问题，无法正确下载该模板，需要该模板的&#xf…...

编程日记 2025/8/10 22:58:53

Java PrintStream 类深度解析

Java PrintStream 类深度解析便捷： 1.直接输出各种数据 2.自动刷新和自动换行（println方法） 3.支持字符串转义 4.自动编码（自动根据环境选择合适的编码方式） 1. 核心定位 PrintStream 是 FilterOutputStream 的子类，提供格式化输出能力，是标准输出 System.out 的…...

编程日记 2025/8/9 1:30:15

超简单的git学习教程

本博客仅用于记录学习和使用前提声明全部内容全部来自下面廖雪峰网站，如果侵权联系我删除 1.小白学习看这篇，快速易懂入门，完整内容（半天完成学习本地和远程仓库建立） 简介 - Git教程 - 廖雪峰的官方网站 2.博客中…...

编程日记 2025/8/6 12:39:44

Yocto项目实战教程-第5章-5.1-5.2小节-BitBake的起源与源代码讲解

🔍 B站相应的视频教程： 📌 Yocto项目实战教程-第5章-5.1-5.2小节-BitBake的起源与源代码讲解记得三连，标为原始粉丝。 📚 系列持续更新中，B站搜索 “嵌入式 Jerry”，系统学 Yocto 不迷路&#…...

编程日记 2025/8/8 8:28:17

SQL注入相关知识

一、布尔盲注 1、布尔盲简介布尔盲注是一种SQL注入攻击技术，用于在无法直接获取数据库查询结果的情况下，通过页面的响应来判断注入语句的真假，从而获取数据库中的敏感信息 2、布尔盲注工作原理布尔盲注的核心在于利用SQL语句的布尔逻辑…...

编程日记 2025/8/10 22:58:55

Linux网络编程深入解析Linux TCP：TCP实操，三次握手和四次挥手的底层分析

知识点1【TCP编程概述】 1、TCP的概述客户端：主动连接服务器，和服务器进行通信服务器：被动被客户端连接，启动新的线程或进程，服务器客户端（并发服务器） 这里重复TCP和UDP特点 TCP&#x…...

编程日记 2025/8/10 0:47:50

实验4基于神经网络的模式识别实验

实验原理 1. BP学习算法是通过反向学习过程使误差最小，其算法过程从输出节点开始，反向地向第一隐含层(即最接近输入层的隐含层)传播由总误差引起的权值修正。BP网络不仅含有输入节点和输出节点，而且含有一层或多层隐(层)节点。输入信号先向前…...

编程日记 2025/8/10 22:58:52

Rust网络编程实战：全面掌握reqwest库的高级用法

一、开篇导引 1.1 对比Python Requests解释为何reqwest是Rust生态的标杆HTTP客户端在Python生态中，Requests 库以其简洁易用的API成为了HTTP客户端的首选。它使得开发者能够轻松地发送各种HTTP请求，处理响应，而无需过多关注底层细节。然而…...

编程日记 2025/8/10 23:00:48

【漫话机器学习系列】211.驻点（Stationary Points）

驻点（Stationary Points）：理解函数导数为零的关键位置在数学分析、机器学习优化、物理建模等领域中，驻点（Stationary Points）是一个非常重要的概念。它们是函数图像中“停下来的点”，即导数为…...

编程日记 2025/8/10 22:57:06

图 - 最小生成树算法 - Kruskal - Prim

目录前言什么是最小生成树算法 Kruskal 克鲁斯卡尔 Prim 普利姆结语前言在图中一共有两类算法，一种是最短路径，还有一种就是本篇要讲解的最小生成树算法了其中，最短路径一共有三种，而最小生成树一共有两种&#xff…...

编程日记 2025/8/7 21:48:07

linux kernel irq相关函数详解

在Linux内核驱动开发中，处理中断涉及一系列关键函数，正确使用这些函数对确保驱动的稳定性和性能至关重要。以下是disable_irq、free_irq、platform_get_irq和request_irq等函数的详细解析，涵盖其功能、用法、注意事项及示例代码。一、核心函…...

编程日记 2025/8/10 23:03:18

聊聊Doris的数据模型，如何用结构化设计解决实时分析难题

传统 OLAP 系统的局限在大数据实时分析领域，数据模型设计直接决定了系统的查询性能、存储效率与业务适配性。Apache Doris作为新一代MPP分析型数据库，通过独创的多模型融合架构，在业内率先实现了"一份数据支持多种分析范式"的能力…...

编程日记 2025/8/10 23:01:12

[Swift]Xcode模拟器无法请求http接口问题

1.以前偷懒一直是这样设置 <key>NSAppTransportSecurity</key> <dict><key>NSAllowsArbitraryLoads</key><true/> </dict> 现在我在Xcode16.3上，这种设置方式在真机上能请求http（应该是设备开启了开发者模式…...

编程日记 2025/8/10 22:56:34

首先启动 zookeeper /home/kafka/bin/zookeeper-server-start.sh /home/kafka/config/zookeeper.properties 创建SCRAM证书 /home/kafka/bin/kafka-configs.sh --zookeeper localhost:2181 --alter --add-config SCRAM-SHA-256[iterations8192,passwordliebe],SCRAM-SHA-512[p…...

编程日记 2025/8/10 22:56:34

前言

一、初识线段树

图例：

数组存储：

指针存储：

理由：

build函数建树

二、线段树的区间修改维护

区间修改维护：

区间修改的操作：

递归更新过程：

区间修改update：

三、线段树的区间查询

区间查询：

区间查询的操作：

递归查询过程：

区间查询query：

例题：

完整代码：

数组实现：

指针实现：

总结

相关文章：