当前位置：首页 > news >正文

图 - 最小生成树算法 - Kruskal - Prim

news 来源：原创 2025/8/10 23:05:24

前言

什么是最小生成树算法

Kruskal 克鲁斯卡尔

Prim 普利姆

结语

前言

在图中一共有两类算法，一种是最短路径，还有一种就是本篇要讲解的最小生成树算法了

其中，最短路径一共有三种，而最小生成树一共有两种，也就是克鲁斯卡尔（Kruskal）和普利姆算法（Prim）

至于最短路径算法，我们会在下一篇进行讲解

同时需要注意的是，下面的两种算法我们都会用邻接矩阵进行代码书写！！！（绝对不是因为他的代码比较好写）

同时，我们下面还会一直用到边，所以我们需要额外写一个类来表示边，如下：

    struct Edge{size_t _srci;size_t _dsti;W _w;Edge(size_t src, size_t dst, const W& w):_srci(src),_dsti(dst),_w(w){}bool operator>(const Edge& e) const{return _w > e._w;}};

什么是最小生成树算法

首先我们可以举一个例子帮忙理解，你，是一个城市路线规划师，现在要建各个地区之间的铁路，问你怎么样修铁路，怎么规划路线才能用最小的利益将所有城市链接起来

每一个城市之间都有相应的边的权重，有可能从 A 到 B 之间有一座大山，直接过去要挖隧道，但是从 C 绕过去的话就会便宜很多

而我们的图本质上就是边和节点构成的，我们每一条边都有相应的权重，最小生成树问的就是，如何让所有节点都连起来并且利益最大化

这时我们就有两个算法可以选择了，一个叫做克鲁斯卡尔，还有一个叫做普利姆，这两个都是人名，也就是这两个大佬发明出来的

而这两个算法本质上都是用的贪心算法，也就是每一次都直接选最小的边，只不过各自的思考方式是不一样的，这也就导致了两个算法各有特色，虽然都是贪心

Kruskal 克鲁斯卡尔

我们的克鲁斯卡尔算法，其实理解起来相当简单，就是在一开始的时候，我们就将所有边都放在小堆（priority_queue）里面，这样我们堆顶存的就是最小的边，然后我们每一次拿出来目前最小的边，一次一次地往图上放边即可

但是但是，这样会面临一个特别严重的问题就是，我们的图一共有 n 个节点（假设），那就意味着如果是最小生成树的情况的话，就必定有且仅有 n-1 条边，因为这样刚好将所有点链接起来

但是如果我们只是一味的往图里面放当前权重最小的边的话，就一定会出现本来两个节点已经链接起来了，但是我们当前权重最小的边又将这两个节点再链接一次的情况，如下：

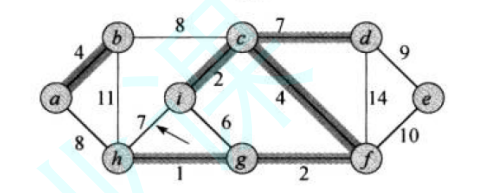
我们会看到，其中点 i 和点 h 已经链接起来了，也就是走的 i->c->f->g->h 这条路，但是当前权重最小的边是 i->h，但是我们是不能选择这条边的，因为本来这两个点就链接起来了，我们最小生成树要的只是全部节点链接起来的同时利益最大化，而不是单纯某两个点之间的利益最大化，如果要单纯两个点的话，那就是我们下一篇要讲的知识点了，也就是最短路径问题

但是接下来又有新的问题了，我们该如何辨认，某两个点之间，是否已经链接起来了呢？

其实这也非常简单，我们在学习图论之前，我们就学过了一个数据结构，叫做并查集

如果我们每一次遍历到一个新节点的时候，我就看看并查集里面，起始节点和当前节点是否是同一个根，这样就能判断这个节点是否已经链接过了

比如上面的，我们一共有两个并查集，假设我们第二个并查集的根就是 d，那么无论是 i 还是 h，他们的根都是 d，所以我们就能判断了，最后我们每加完一条新的边，就将结束节点放进并查集里面

至此，我们的克鲁斯卡尔算法的逻辑就讲完了，单纯的文字可能不太好理解，所以图示如下：

最后代码如下：

    W kruskal(Self& minTree){// 前期准备工作size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (auto& e : minTree._matrix){e.resize(n, MAX_W);}//将所有的边都放进小堆里面priority_queue<Edge, vector<Edge>, greater<Edge>> minque;for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)if (i < j && _matrix[i][j] != MAX_W)minque.push(Edge(i, j, _matrix[i][j]));int size = 0;W total = W();// 这个是并查集UnionFindSet ufs(n);//克鲁斯卡尔算法主逻辑while (!minque.empty()){//每次取出堆顶，也就是权重最小的边Edge min = minque.top();minque.pop();// 判断是否在同一个并查集里面if (ufs.FindRoot(min._srci) != ufs.FindRoot(min._dsti)){minTree.AddEdge(min._srci, min._dsti, min._w);ufs.Union(min._srci, min._dsti);size++;total += min._w;}}if (size == n - 1) return total;else return W();}

Prim 普利姆

看完了上面的 kruskal 算法之后，我们会发现他的思想其实就是纯贪，然后面对成环问题再想办法进行特判

但是我们的 Prim 算法的思想就不一样，他是不需要特判是否成环的

在普利姆的算法思想中，他将所有的点抽象成了两个集合，一个是已经确定了的，也就是已经选过了的点，另一个集合就是还没有选过的点的集合

然后我们会从一个起点出发，每一次我们都去看与这个点链接的其他点，也就是当前点的所有边，然后选取权重最小的那一条，如下:

在这张图里面，我们的起点是 a，然后我们第一次看的时候，就只会关注两条边，a->b 和 a->h，然后选择权重更小的 ab 边，最后将点 b 放进集合里面，已经选过了的点的集合

但是随着我们选边的进行，我们到后面就不是单对一个点进行判断，比如上面，我们选完 b 之后，我们接下来是对 bc、bh、ah 这三条边进行判断，也就是当前选了的边的集合往外扩展的所有边的最小值

同时，我们每一次选择的时候，我们都先看看选过了的集合里面是否有当前点，或者没选过的集合里面有没有当前点，判断出这个点没选过之后，我们再选取与这条边链接的所有的边里面权重最小的边

但是我们还有一个问题就是，第一个，我们怎么选出与当前边相连的边，第二个，怎么选出当前所有选过的边相连的边里面权重最小的边

其实两个问题都很好解决，第一个，由于我们用的是邻接矩阵，所以我们直接遍历起点的那一行即可，比如从 a 位置开始，我们就遍历 ab、ac、ad......但是还需要判断一下，如果邻接矩阵里面记录的当前位置的值为 INT_MAX的话，就代表这条边不存在

接着是第二个问题，我们只需要用一个小堆即可，如下：

我们每一次选的时候，所有选过的节点对应的边都被放进小堆里面了，我们只需要进行取堆顶并且判断权重最小的边的结束位置的节点是否已经被选过即可

至此，我们的 Prim 算法逻辑就全部讲完了，主要思路图示如下：

代码如下：

W Prim(Self& minTree, const V& src){size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (auto& e : minTree){e.resize(n, MAX_W);}size_t srci = _indexMap[src];priority_queue<Edge, vector<Edge>, greater<Edge>> pq;set<size_t> inSet;inSet.insert(srci);for (int i = 0; i < n; i++)if (_matrix[srci][i] != MAX_W)pq.push(Edge(srci, i, _matrix[srci][i]));W total = W();while (!pq.empty() && inSet.size() < n){Edge min = pq.top();pq.pop();if (inSet.find(min.srci) == inSet.end() || inSet.find(min.dsti) == inSet.end()){minTree.AddEdge(min._srci, min._dsti, min._w);total += min._w;for (int i = 0; i < n; i++){if (_matrix[min._dsti][i] != MAX_W && inSet.find(i) == inSet.end())pq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}inSet.insert(min._dsti);}}if (inSet.size() == n) return total;else return W();}

结语

这篇文章到这里就结束啦！！~(￣▽￣)~*

如果觉得对你有帮助的，可以多多关注一下喔

图 - 最小生成树算法 - Kruskal - Prim

目录前言什么是最小生成树算法 Kruskal 克鲁斯卡尔 Prim 普利姆结语前言在图中一共有两类算法，一种是最短路径，还有一种就是本篇要讲解的最小生成树算法了其中，最短路径一共有三种，而最小生成树一共有两种&#xff…...

编程日记 2025/8/10 23:05:24

linux kernel irq相关函数详解

在Linux内核驱动开发中，处理中断涉及一系列关键函数，正确使用这些函数对确保驱动的稳定性和性能至关重要。以下是disable_irq、free_irq、platform_get_irq和request_irq等函数的详细解析，涵盖其功能、用法、注意事项及示例代码。一、核心函…...

编程日记 2025/8/10 23:03:18

聊聊Doris的数据模型，如何用结构化设计解决实时分析难题

传统 OLAP 系统的局限在大数据实时分析领域，数据模型设计直接决定了系统的查询性能、存储效率与业务适配性。Apache Doris作为新一代MPP分析型数据库，通过独创的多模型融合架构，在业内率先实现了"一份数据支持多种分析范式"的能力…...

编程日记 2025/8/10 23:01:12

[Swift]Xcode模拟器无法请求http接口问题

1.以前偷懒一直是这样设置 <key>NSAppTransportSecurity</key> <dict><key>NSAllowsArbitraryLoads</key><true/> </dict> 现在我在Xcode16.3上，这种设置方式在真机上能请求http（应该是设备开启了开发者模式…...

编程日记 2025/8/10 22:56:34

首先启动 zookeeper /home/kafka/bin/zookeeper-server-start.sh /home/kafka/config/zookeeper.properties 创建SCRAM证书 /home/kafka/bin/kafka-configs.sh --zookeeper localhost:2181 --alter --add-config SCRAM-SHA-256[iterations8192,passwordliebe],SCRAM-SHA-512[p…...

编程日记 2025/8/10 22:56:34

基于STM32中断讲解

基于STM32中断讲解一、NVIC讲解简介：当一个中断请求到达时，NVIC会确定其优先级并决定是否应该中断当前执行的程序，以便及时响应和处理该中断请求。这种设计有助于提高系统的响应速度和可靠性，特别是在需要处理大量中断请求的实…...

编程日记 2025/8/10 22:54:23

Java 动态代理教程（JDK 动态代理）（以RPC 过程为例）

1. 什么是动态代理在运行时为指定的接口自动生成代理对象，并通过 invoke 方法增强了这些对象的功能 2. 两个核心组件 java.lang.reflect.Proxy类这个类提供了方法：newProxyInstance()用来创建一个代理对象 public static Object newProxyInstance(…...

编程日记 2025/8/3 20:03:00

Linux Privilege Escalation： LD_PRELOAD

声明：本文所有操作需在授权环境下进行，严禁非法使用！ 0x01 什么是 LD_PRELOAD？ LD_PRELOAD 是 Linux 系统中一个特殊的环境变量，它允许用户在程序启动时优先加载自定义的动态链接库（.so 文件）&…...

编程日记 2025/8/10 22:54:25

Java 并发性能优化：线程池的最佳实践

Java 并发性能优化：线程池的最佳实践在 Java 并发编程的世界里，线程池堪称提高应用性能与稳定性的神器。恰如其分地运用线程池，能让我们在多线程任务调度时游刃有余，既能避免线程频繁创建销毁带来的开销，又能合理管控…...

编程日记 2025/8/10 22:57:07

QML动画--ParallelAnimation和SequentialAnimation

一、ParallelAnimation ParallelAnimation 是 QML 中用于并行执行多个动画的容器动画类型，可以同时运行多个子动画。基本用法 qml import QtQuick 2.15Rectangle {id: rectwidth: 100; height: 100color: "red"x: 0; y: 0; opacity: 1.0ParallelAnim…...

编程日记 2025/8/10 22:54:34

深入解析进程与线程：区别、联系及Java实现

引言在现代操作系统中，进程和线程是并发编程的两大核心概念。理解它们的区别与联系对开发高性能、高可靠性的程序至关重要。本文将通过原理分析和Java代码示例，深入探讨这两个关键概念。一、基本概念 1.1 进程（Process） 定义&…...

编程日记 2025/8/10 22:54:35

c++：线程（std::thread）

目录从第一性原理出发：为什么需要线程？ ✅ 本质定义： 📌 使用基本语法： 线程之间的“并发”与“并行”的区别线程安全与数据竞争（Race Condition） 如何让线程“安全地”访问数据&#x…...

编程日记 2025/8/10 22:59:13

基于LSTM-AutoEncoder的心电信号时间序列数据异常检测(PyTorch版)

心电信号（ECG）的异常检测对心血管疾病早期预警至关重要，但传统方法面临时序依赖建模不足与噪声敏感等问题。本文使用一种基于LSTM-AutoEncoder的深度时序异常检测框架，通过编码器-解码器结构捕捉心电信号的长期时空依赖特征&#…...

编程日记 2025/8/10 21:36:24

[密码学基础]GM/T 0018-2023 密码设备应用接口规范深度解析：技术革新与开发者实践

GM/T 0018-2023 密码设备应用接口规范深度解析：技术革新与开发者实践 GM/T 0018-2023《密码设备应用接口规范》是中国密码行业的重要标准，于2023年12月4日发布，2024年6月1日正式实施，替代了2012年版标准。该标准旨在规范密码设备…...

编程日记 2025/8/10 22:54:22

深入理解 Java 多线程：锁策略与线程安全

文章目录一、常见的锁策略1. 乐观锁&&悲观锁2. 读写锁3. 重量级锁&&轻量级锁4. 自旋锁5. 公平锁&&不公平锁6. 可重入锁 && 不可重入锁二、CAS1. 什么是 CAS2. CAS 是怎么实现的3.CAS 有哪些应用1) 实现原子类2) 实现自旋锁 4. CAS 的 ABA 问…...

编程日记 2025/8/10 22:54:34

Java从入门到“放弃”（精通）之旅——数组的定义与使用⑥

Java从入门到“放弃”（精通）之旅🚀——数组⑥ 前言——什么是数组？ 数组：可以看成是相同类型元素的一个集合，在内存中是一段连续的空间。比如现实中的车库，在java中，包含6个整形类…...

编程日记 2025/8/10 22:56:32

VsCode搭建

安全性问题的声明： VScode是一个由微软出品的开源软件编辑器 VScode下载 https://code.visualstudio.com/Download 官网直接下载即可，windows和linux的vscode使用命令是类似的。 VScode插件相关为了方便安装，推荐设置并使用vscode插件的…...

编程日记 2025/8/8 15:03:24

【NLP 65、实践 ⑯ 基于Agent优化文章】

羁绊由我而起，痛苦也由我承担 —— 25.4.18 一、⭐【核心函数】定义大模型调用函数 call_large_model prompt：用户传入的提示词（如 “请分析这篇作文的主题”），指导模型执行任务 client：Zhipu…...

编程日记 2025/8/9 5:43:14

【Redis】从单机架构到分布式，回溯架构的成长设计美学

前言 🌟🌟本期讲解关于分布式架构的发展相关知识介绍~~~ 🌈感兴趣的小伙伴看一看小编主页：GGBondlctrl-CSDN博客 🔥 你的点赞就是小编不断更新的最大动力 🎆那么废…...

编程日记 2025/8/10 5:07:10

增量式PID基础解析与代码实例：温控系统

目录 1. 前言 2. 增量式PID控制的基本原理 2.1 PID控制的基本概念 2.2 增量式PID控制的特点 3. 增量式PID控制的Python实现：温控系统 3.1 构建增量式PID控制器 3.2 使用增量式PID控制器 3.3 运行模拟 3.4 完整代码 4. 参数调整与优化 4.1 参数选择 4.2…...

编程日记 2025/8/10 7:19:49

数据结构——栈以及相应的操作

栈(Stack) 在维基百科中是这样定义的： 堆栈(stack) 又称为栈或堆叠，是计算机科学中的一种抽象资料类型，只允许在有序的线性资料集合中的一端（称为堆栈顶端，top）进行加入数据（push）和…...

编程日记 2025/7/31 7:26:48

opencv 图像的旋转

图像的旋转 1 单点旋转2. 图片旋转（cv2.getRotationMatrix2D）3. 插值方法3.1 最近邻插值(cv2.INTER_NEAREST)3.2 双线性插值(cv2.INTER_LINEAR)3.3 像素区域插值（cv2.INTER_AREA）3.4 双三次插值（cv2.INTER_CUBIC&#…...

编程日记 2025/8/10 22:54:24

P3916 图的遍历

P3916 图的遍历题目来源-洛谷题意有向图中，找出每个节点能访问到的最大的节点思路每个节点的最大节点，不是最长距离，如果是每个节点都用dfs去找最大值，显然1e6*1e6 超时了，只能60分从第一个节点开始遍历&…...

编程日记 2025/8/10 23:03:17

Vue3 + Three.js 场景编辑器开发实践

文章目录前言项目背景与意义项目技术栈在线演示核心功能实现1. 智能化场景管理2. 专业级模型处理3. 可视化材质与照明4. 相机与渲染引擎5. 场景操作项目优势开发目标1. 几何模型和模型导入，场景新建按钮增加2. 提供场景内容的可视化编辑功能3. 渲染器场景&#xf…...

编程日记 2025/8/10 23:03:17

Vue3 本地打包启动白屏解决思路！! !

“为什么我访问 http://127.0.0.1:5501/index.html 白屏，删了 index.html 再访问 / 就又活过来了？” —— 你的项目与 SPA 路由的“宫斗大戏” 一、问题复现场景本地通过 VSCode Live Server（或其他静态服务器）启动了打包后的 V…...

编程日记 2025/8/8 4:29:57

Ubuntu 安装 Docker 教程（官方推荐方式）

✅ 步骤 1：卸载旧版本（如果有） for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done---### ✅ 步骤 2：更新 APT 索引并安装依赖项bash sudo a…...

编程日记 2025/8/10 23:01:10

WPF 点击按钮，显示隐藏另一个控件

<Button Content"显示隐藏" Click"operationDetails_Click" /> private void operationDetails_Click(object sender, RoutedEventArgs e) { 另一个控件的Name.Visibility 另一个控件的Name.Visibility Visibility.Visible ? Visibility.Col…...

编程日记 2025/8/10 23:00:46

RBAC的使用

1、简述RBAC的作用及工作流程 Rbac基于角色访问控制，用于管理用户对集群资源的访问权限，通过定义角色和绑定规则，将用户与权限进行关联，作用：权限精细化管理，操作便捷与统一管理，动态调整权限。…...

编程日记 2025/8/10 22:59:11

QML中的3D功能--模型导入与修改

在Qt 3D中导入和修改3D模型是开发3D应用程序的基础。以下是详细的流程和技术方案：一、模型导入基础 1. 支持的文件格式 Qt 3D支持多种3D模型格式： OBJ (Wavefront) FBX (Autodesk) DAE (Collada) GLTF/GLB (推荐格式) STL (3D打印格式) 2. 基本导入方法 qml import Qt3…...

编程日记 2025/8/5 4:22:52

树莓派超全系列教程文档--(33)树莓派启动选项

树莓派启动选项启动选项start_file ，fixup_filecmdlinekernelarm_64bitramfsfileramfsaddrinitramfsauto_initramfsdisable_poe_fandisable_splashenable_uartforce_eeprom_reados_prefixotg_mode （仅限Raspberry Pi 4）overlay_prefix配置属…...

编程日记 2025/8/10 1:09:17

dotnet core webapi 实现异常处理中间件

目录第一步：创建异常处理中间件类（自定义响应格式） 第二步：在 Program.cs 中使用中间件三、效果第一步：创建异常处理中间件类（自定义响应格式） public static class ExceptionMiddleware…...

编程日记 2025/8/8 17:51:32

实现Azure Function安全地请求企业内部API返回数据

需要编写一个Function在Azure云上运行，它需要访问企业内部的API获取JSON格式的数据，企业有网关和防火墙，API有公司的okta身份认证，通过公司的域账号来授权访问，现在需要创建一个专用的域账号，让Function访问…...

编程日记 2025/8/8 18:39:14

实现Azure Databricks安全地请求企业内部API返回数据

需要编写一个Databricks在Azure云上运行，它需要访问企业内部的API获取JSON格式的数据，企业有网关和防火墙，API有公司的okta身份认证，通过公司的域账号来授权访问，现在需要创建一个专用的域账号，让Databrick…...

编程日记 2025/7/31 7:26:24

结合建筑业务讲述TOGAF标准处理哪种架构

TOGAF标准处理哪种架构内容介绍业务架构业务策略，治理，组织和关键业务流程数据架构组织的逻辑和物理数据资产以及数据管理资源的结构应用架构待部署的各个应用程序，它们之间的交互以及与组织核心业务流程的关系的蓝图技术架构支持业务&#…...

编程日记 2025/8/5 1:20:54

深度学习--卷积神经网络CNN原理

文章目录一、CNN图像原理1、了解CNN如何处理图像二、CNN图像识别1、画面不变性2、主要表现1）平移不变性2）尺度不变性3）旋转不变性 3、传统神经网络1）数据预处理2）特征提取3）搭建神经网络模型4&#xff09…...

编程日记 2025/8/10 10:32:01

PostgreSQL 常用客户端工具

PostgreSQL 常用客户端工具 PostgreSQL 拥有丰富的客户端工具生态系统，以下是各类常用工具的详细分类和介绍： 一图形化客户端工具 1.1 跨平台工具工具名称特点适用场景许可证pgAdmin官方出品，功能全面开发/运维PostgreSQLDBeaver支持多…...

编程日记 2025/8/9 18:48:50

PostgreSQL数据库yum方式安装详解

PostgreSQL数据库yum方式安装 1. 基础环境配置2. 前期安装准备3. 软件安装3.1 YUM方式安装（PG 13）3.1.1 安装rpm仓库3.1.2 安装软件包PG133.1.3 初始化数据库3.1.4 启动数据库3.1.5 开机自启动3.1.6 编辑环境变量 4. 安装后配置 1. 基础环境配置 2. 前期…...

编程日记 2025/8/8 16:38:05

浅析vue2和vue3的区别

以下是 Vue 2 和 Vue 3 的主要区别：一、核心特性 1. 响应式机制 Vue 2：基于 Object.defineProperty 实现响应式。无法检测对象属性的新增和删除，需要使用 Vue.set 或 $set。Vue 3：使用 Proxy 替代 Object.defineProperty。能够直接检测对象属性的新增和删除，无需额外方…...

编程日记 2025/8/4 1:54:14

【Linux我做主】make和makefile自动化构建

make和makefile自动化构建 make和makefile自动化构建github地址前言背景介绍为什么需要make和makefile？ make和makefile解析什么是make和makefile依赖关系和依赖方法核心语法结构简单演示编译清理多阶段编译示例 make时执行的顺序场景1：clean目标在前(特…...

编程日记 2025/8/4 23:32:04

spring boot应用部署IIS

Windows IIS 部署 Spring Boot 应用详细指南本文档提供了在 Windows Server 上使用 IIS 部署 Spring Boot 应用的完整步骤和最佳实践。目录概述前期准备Spring Boot 应用准备安装配置必要组件配置 IIS 站点配置反向代理配置 Windows 服务配置应用自启动HTTPS 配置日志配置…...

编程日记 2025/8/6 18:30:01

Linux系统之部署TestNet资产管理系统

Linux系统之部署TestNet资产管理系统一、TestNet 介绍1.1 TestNet简介1.2 主要特点1.3 主要使用场景二、本次实践规划2.1 本地环境规划2.2 本次实践介绍三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本四、部署TestNet系统4.1 下载T…...

编程日记 2025/8/5 4:47:20

@EnableAsync+@Async源码学习笔记之六

接上文，我们本文分析 AsyncExecutionAspectSupport 的源码： package org.springframework.aop.interceptor;import java.lang.reflect.Method; import java.util.Map; import java.util.concurrent.Callable; import java.util.concurrent.CompletableFu…...

编程日记 2025/8/8 1:20:12

SQL系列：常用函数

1、【MySQL】合并字段函数（列转行） 它可以将两个字段中的数据合并到一个字段中。 1）CONCAT函数 CONCAT函数可以将多个字段中的数据合并到一个字段中。它的语法格式如下： SELECT CONCAT(字段1,字段2,...字段N) FROM 表名;SELEC…...

编程日记 2025/8/5 1:12:40

Git 中修改某个特定的commit提交内容

在 Git 中修改某个特定的提交（commit）通常需要使用交互式变基（Interactive Rebase） 或修改提交（Commit Amend）。以下是不同场景下的具体操作步骤： 一、修改最近的提交（最新提交&am…...

编程日记 2025/8/5 1:33:47

FHS --- linux目录结构（部分目录解释）

根目录（/） 的意义和内容 ： 根目录是整个系统最重要的一个目录，因为不但所有的目录都是由根目录衍生出来的，同时根目录也与开机/还原/系统修复等动作有关。由于系统开机时需要特定的开机软件、核心档案、开机所需程序…...

编程日记 2025/8/6 2:25:06

不带无线网卡的Linux开发板上网方法

I.MX6ULL通过网线上网设置WLAN共享修改开发板的IP 在使用I.MX6ULL-MINI开发板学习Linux的时候，有时需要更新或者下载一些资源包，但是开发板本身是不带无线网卡或者WIFI芯片的，尝试使用网口连接笔记本，笔记本通过无线网卡连接WIFI…...

编程日记 2025/7/31 7:25:59

图书管理系统C语言

图书管理系统C语言代码示例。该系统可以实现图书信息（包含图书编号、书名、作者、出版社、价格、库存数量）的录入、显示、查询、修改、删除等功能，还具备一定的错误处理和输入验证。 #include <stdio.h> #include <stdlib.h> …...

编程日记 2025/8/6 9:01:25

关于大型语言模型的“生物学”

我知道我们已经聊过很多次，关于LLM是怎么运作的，它们的影响力，还有它们的使用场景。但尽管现在有那么多讲LLM的文章，它们本质上还是个黑箱。但我们真正要问自己的问题是，为什么理解这些系统的内部结构很重要&#xf…...

编程日记 2025/8/5 13:43:34

图像预处理-图像边缘检测(流程)

一.高斯滤波因为图像边缘检测就是把像素值有差异的地方提取出来，所以噪声会有很大影响，因此需要对图像进行平滑处理，高斯滤波是流程中常用的方法。二.计算图像的梯度与方向过程中通常使用sobel算子进行梯度计算，在OpenCV中&am…...

编程日记 2025/8/8 18:18:03

解锁思想道德修养的奥秘：用思维导图开启智慧之旅

在我们的成长过程中，思想道德修养如同基石，奠定了我们为人处世、面对生活挑战的基本态度和准则。而如何高效地梳理和掌握思想道德修养的丰富内容呢？思维导图这一强大工具为我们提供了独特视角和便捷途径。思想道德修养的关键板块道德理论…...

编程日记 2025/8/7 9:21:52

前言

什么是最小生成树算法

Kruskal 克鲁斯卡尔

Prim 普利姆

结语

相关文章：