当前位置：首页 > news >正文

复变函数摘记3

news 来源：原创 2025/8/27 5:28:45

复变函数摘记3

5. 留数
- 5.1 可去奇点、极点、本性奇点
- 5.2 零点与极点的关系
- 5.3 在无穷远点处的情形
- 5.4 留数

5. 留数

$\quad$ 如果函数 $f (z)$ 在 $z_0$ 及 $z_0$ 的邻域内处处可导，那么称 $f (z)$ 在点 $z_0$ 处解析。
$\quad$ 如果函数 $f (z)$ 在点 $z_0$ 处不解析，那么 $z_0$ 为 $f (z)$ 的奇点。

定义　如果函数 $f (z)$ 在 $z_0$ 不解析，但是在 $z_0$ 的某个去心邻域 $0<|z-z_0|<\delta$ 内处处解析，那么 $z_0$ 称为 $f (z)$ 的孤立奇点。

$\quad$ 例如，函数 $\frac{1}{z},\ e^{\frac{1}{z}}$ 都以 $z = 0$ 为孤立奇点；当 $z=\infty$ 为孤立奇点，其去心邻域为 $R<|z|<+\infty$ 。

5.1 可去奇点、极点、本性奇点

$\quad$ 由洛朗级数的定义可知，函数 $f (z)$ 在其孤立奇点 $z_0$ 的去心邻域内可以展开成洛朗级数。根据展开式的不同情况，可以将孤立奇点划分为可去奇点、极点和本性奇点：

$\quad(1)$ 如果 $z_0$ 为 $f (z)$ 的可去奇点，那么 $\displaystyle\lim_{z\to z_0}f(z)$ 存在、且有限
$\quad(2)$ 如果 $z_0$ 为 $f (z)$ 的极点，那么 $\displaystyle\lim_{z\to z_0}f(z)=\infty$
$\quad(3)$ 如果 $z_0$ 为 $f (z)$ 的本性奇点， $\displaystyle\lim_{z\to z_0}f(z)$ 不存在、且不为 $\infty$

$\bullet\quad$ 可去奇点

定义　如果在洛朗级数中不含 $z-z_0$ 的负幂项，那么孤立奇点 $z_0$ 称为 $f (z)$ 的可去奇点。

$\quad$ 此时， $f (z)$ 在 $z_0$ 的去心邻域内的洛朗级数，就是一个普通幂级数

$\qquad\qquad$ $f(z)=\textcolor{blue}{c_0+c_{1}(z-z_0)+\cdots+c_{n}(z-z_0)^{n}+\cdots}$

$\quad$ 因此，该幂级数的和函数 $F (z)$ 是在 $z_0$ 解析的函数，且当 $z\neq z_0$ 时， $F (z) = f (z)$ ；当 $z=z_0$ 时， $F(z_0)=c_0$ 。

$\quad$ 由于 $\displaystyle\lim_{z\to z_0}f(z)=\lim_{z\to z_0}F(z)=F(z_0)=c_0$ ，所以不论 $f (z)$ 原来在 $z_0$ 处是否有定义，如果我们令 $f(z_0)=c_0$ ，那么在圆域 $|z-z_0|<\delta$ 内就有 $\textcolor{blue}{f(z)=c_0+c_{1}(z-z_0)+\cdots+c_{n}(z-z_0)^{n}+\cdots}$ ，从而函数 $f (z)$ 在 $z_0$ 处就成为解析的。

例如， $z = 0$ 是 $\dfrac{\sin z}{z}$ 的可去奇点
在 $z = 0$ 的去心邻域内的洛朗级数 $\dfrac{\sin z}{z}=\dfrac{1}{z}\left(z-\dfrac{1}{3!}z^3+\dfrac{1}{5!}z^5-\cdots\right)=1-\dfrac{1}{3!}z^2+\dfrac{1}{5!}z^4-\cdots$ 不含负幂项
如果我们令 $\dfrac{\sin z}{z}$ 在 $z = 0$ 的值为 $1$ ，即 $c_0=1$ ，那么 $\dfrac{\sin z}{z}$ 在 $z = 0$ 就成为解析的。

$\bullet\quad$ 极点

定义　如果在洛朗级数中只有有限多个 $z-z_0$ 的负幂项，且其中关于 $z-z_0)^{-1}$ 的最高幂为 $z-z_0)^{-m}$ ，那么孤立奇点 $z_0$ 称为 $f (z)$ 的 $m$ 级极点。

$\quad$ 即：　 $\textcolor{blue}{f(z)=c_{-m}(z-z_0)^{-m}+\cdots+c_{-2}(z-z_0)^{-2}+c_{-1}(z-z_0)^{-1}+c_0+c_{1}(z-z_0)+\cdots}$

$\quad$ 上式也可以写成：　 $f(z)=\textcolor{darkblue}{\dfrac{\textcolor{crimson}{g(z)}}{(z-z_0)^m}}$

$\quad$ 且　　　　　　　 $\textcolor{crimson}{g(z)}=\textcolor{darkblue}{c_{-m}+c_{-m+1}(z-z_0)+c_{-m+2}(z-z_0)^2+\cdots}$

$\quad$ 其中， $\textcolor{crimson}{g(z)}$ 是 $|z-z_0|<\delta$ 内的解析函数（不含负幂项），且 $g(z_0)\neq0$
　
$\blacktriangleright$ 　反过来，当任一函数可以表示为 $f(z)=\textcolor{blue}{\dfrac{\textcolor{crimson}{g(z)}}{(z-z_0)^m}}$ ，且 $g(z_0)\neq0$ 时，那么 $z_0$ 是函数 $f (z)$ 的 $m$ 级极点。

$\blacktriangleright$ 　如果 $z_0$ 为 $f (z)$ 的极点，由 $f(z)=\textcolor{blue}{\dfrac{\textcolor{crimson}{g(z)}}{(z-z_0)^m}}$ ，就有 $\displaystyle\lim_{z\to z_0}|f(z)|=+\infty$ 或 $\displaystyle\lim_{z\to z_0}f(z)=\infty$

例如，对于有理分式函数 $f(z)=\dfrac{z-2}{(z^2+1)(z-1)^3}$ ， $z = 1$ 是一个 $3$ 级极点， $z=\pm\text{i}$ 是 $1$ 级极点。

$\bullet\quad$ 本性极点

定义　如果在洛朗级数中含有无穷多个 $z-z_0$ 的负幂项，那么孤立奇点 $z_0$ 称为 $f (z)$ 的本性奇点。

$\quad$ 如果 $z_0$ 为函数 $f (z)$ 的本性奇点，那么对于任意给定的复数 $A$ ，总可以找到一个趋于 $z_0$ 的数列，当 $z$ 沿这个数列趋向于 $z_0$ 时， $f(z)\to A$ 。

$\quad$ 例如，由于 $e^{\frac{1}{z}}=1+z^{-1}+\frac{1}{2!}z^{-2}+\cdots+\frac{1}{n!}z^{-n}+\cdots$ 中有无穷多个 $z$ 的负幂项，因此函数 $f(z)=e^{\frac{1}{z}}$ 以 $z = 0$ 为它的本性奇点。
$\quad$

5.2 零点与极点的关系

定义　不恒等于零的解析函数 $f (z)$ 如果能表示成 $f(z)=(z-z_0)^m\varphi(z)$ ，其中 $\varphi(z)$ 在 $z_0$ 解析并且 $\varphi(z_0)\neq0$ ， $m$ 为正整数，那么 $z_0$ 称为函数 $f (z)$ 的 $m$ 级零点。
　
定理　如果 $f (z)$ 在 $z_0$ 解析，那么 $z_0$ 是 $f (z)$ 的 $m$ 级零点的充要条件是： $f^{(n)}(z_0)=0\ (n=0,1,\cdots,m-1),f^{(m)}(z_0)\neq0$ 。

证：将 $\varphi(z)$ 在 $z_0$ 处展开成泰勒级数： $\varphi(z)=c_0+c_1(z-z_0)+c_2(z-z_0)^2+\cdots$ ，且 $c_0\neq0$
由 $f(z)=(z-z_0)^m\varphi(z)$ 可得到 $f (z)$ 在 $z_0$ 处的泰勒级数为：
　 $f(z)=c_0(z-z_0)^m+c_1(z-z_0)^{m+1}+c_2(z-z_0)^{m+2}+\cdots$ ，第 $n$ 项的系数为 $\dfrac{f^{(n)}(z_0)}{n!}$
显然，前 $m$ 项系数都为零，即 $f^{(n)}(z_0)=0\ (n=0,1,\cdots,m-1)$ ，而 $\dfrac{f^{(m)}(z_0)}{m!}=c_0\neq0$

例如， $z = 0, z = 1$ 分别是函数 $f(z)=z(z-1)^3$ 的 $1$ 级和 $3$ 级零点
例如， $z = 1$ 是函数 $f(z)=z^3-1$ 的 $1$ 级零点，由于 $f^\prime(1)=3z^2|_{z=1}=3\neq0$
　
$\textcolor{red}{\bigstar}\quad$ 一个不恒等于零的解析函数的零点是孤立的。

$\quad$ 由于 $\varphi(z)$ 在 $z_0$ 解析并且 $\varphi(z_0)\neq0$ ，因此 $\varphi(z)$ 在 $z_0$ 邻域内不为零，从而 $f(z)=(z-z_0)^m\varphi(z)$ 在 $z_0$ 的去心邻域内不为零（只在 $z_0$ 处为零）。

由于 $\varphi(z)$ 在 $z_0$ 解析，那么 $\varphi(z)$ 在 $z_0$ 连续，即 $\displaystyle\lim_{z\to z_0}\varphi(z)=\varphi(z_0)$ ，由极限定义
若令 $\varepsilon=\frac{1}{2}|\varphi(z_0)|$ ，必存在 $\delta>0$ ，当 $|z-z_0|<\delta$ 时，有 $|\varphi(z)-\varphi(z_0)|<\varepsilon=\frac{1}{2}|\varphi(z_0)|$
由此得到 $|\varphi(z)|>\frac{1}{2}|\varphi(z_0)|$ ，因此 $\varphi(z)$ 在 $z_0$ 邻域内不为零

定理　如果 $z_0$ 是函数 $f (z)$ 的 $m$ 级极点，那么 $z_0$ 就是 $\dfrac{1}{f(z)}$ 的 $m$ 级零点；反之也成立。
$\quad$

5.3 在无穷远点处的情形

$\quad$ 如果函数 $f (x)$ 在无穷远点 $z=\infty$ 的去心邻域 $R<|z|<+\infty$ 内解析，那么称点 $\infty$ 为 $f (x)$ 的孤立奇点。

$\quad$ 分析方法：做变换 $t=\dfrac{1}{z}$ ，那么
$\quad(1)$ 扩充 $z$ 平面上的无穷远点 $z=\infty$ ，映射成扩充 $t$ 平面上的点 $t = 0$
$\quad(2)$ 扩充 $z$ 平面上无穷远点 $z=\infty$ 的去心邻域 $R<|z|<+\infty$ ，映射成扩充 $t$ 平面上原点的去心邻域 $0<|t|<\frac{1}{R}$

$\quad$ 若令 $f(z)=f(\dfrac{1}{t})=\varphi(t)$ ，就可以把在去心邻域 $R<|z|<+\infty$ 内、对函数 $f (z)$ 的研究转化为在去心邻域 $0<|t|<\frac{1}{R}$ 内、对函数 $\varphi(t)$ 的研究。由于 $f (x)$ 在无穷远点 $z=\infty$ 的去心邻域 $R<|z|<+\infty$ 内解析，那么 $\varphi(t)$ 在去心邻域 $0<|t|<\frac{1}{R}$ 内也是解析的，所以 $t = 0$ 是 $\varphi(t)$ 的可去奇点。

$\quad$ 由于 $f (x)$ 在圆环域 $R<|z|<+\infty$ 内解析，在该圆环域内的洛朗级数展开式为（其中， $C$ 为该圆环域内绕原点的任何一条正向简单闭曲线）：

$\qquad\quad\begin{aligned}f(z)&=\sum_{n=1}^\infty c_{-n}z^{-n}+\sum_{n=0}^\infty c_nz^n \\ &=\sum_{n=1}^\infty c_{-n}z^{-n}+c_0+\sum_{n=1}^\infty c_nz^n \ , \ c_n=\dfrac{1}{2\pi\text{i}}\displaystyle\oint_C\dfrac{f(\zeta)}{\zeta^{n+1}}\mathrm{d}\zeta\ \ (n=0,\pm1,\pm2,\cdots) \end{aligned}$

$\quad$ 由 $t=z^{-1}$ ， $\varphi(t)$ 在圆环域 $0<|t|<\dfrac{1}{R}$ 内解析，在该圆环域内的洛朗级数展开式为：

$\qquad\quad\varphi(t)=\displaystyle\sum_{n=1}^\infty c_{-n}t^{n}+c_0+\sum_{n=1}^\infty c_nt^{-n}$

$\quad$ 由 5.1 可知，在 $\varphi(t)$ 的洛朗级数展开式中
$\quad(1)$ 若不含负项幂，则 $t = 0$ 是 $\varphi(t)$ 的可去奇点
$\quad(2)$ 若含有有限多的负项幂，且 $t^{-m}$ 为最高负幂，则 $t = 0$ 是 $\varphi(t)$ 的 $m$ 级极点
$\quad(3)$ 若含有无限多的负项幂，则 $t = 0$ 是 $\varphi(t)$ 的本性奇点

$\quad$ 由 $\varphi(t)$ 与 $f (x)$ 的关系，可得到在 $f (x)$ 的洛朗级数展开式中就有：
$\quad(1)$ 若不含正项幂，则 $z=\infty$ 是 $f (x)$ 的可去奇点
$\quad(2)$ 若含有有限多的正项幂，且 $z^{m}$ 为最高正幂，则 $z=\infty$ 是 $f (x)$ 的 $m$ 级极点
$\quad(3)$ 若含有无限多的正项幂，则 $z=\infty$ 是 $f (x)$ 的本性奇点
$\quad$

5.4 留数

$\quad$ 如果 $f (z)$ 在 $z_0$ 的邻域内解析，由柯西-古萨基本定理，就有 $\displaystyle\oint_Cf(z)\mathrm{d}z=0$ ，其中 $C$ 为 $z_0$ 邻域内的任意一条简单闭曲线。

$\bullet\quad$ 留数

$\quad$ 如果 $z_0$ 为 $f (z)$ 的一个孤立奇点，那么沿着在 $z_0$ 的某个去心邻域 $R<|z|<+\infty$ 内、包含 $z_0$ 的任意一条正向简单闭曲线 $C$ 的积分 $\displaystyle\oint_Cf(z)\mathrm{d}z$ 一般不等于零，为了计算该积分：

$\quad(1)$ 首先，将函数 $f (z)$ 在该圆环域 $R<|z|<+\infty$ 内展开成洛朗级数：

$\qquad\quad\begin{aligned}\textcolor{blue}{f(z)}=&\cdots+c_{-n}(z-z_0)^{-n}+\cdots+c_{-1}(z-z_0)^{-1}\\&+c_0+c_1(z-z_0)+\cdots+c_{n}(z-z_0)^{n}+\cdots \end{aligned}$

$\quad(2)$ 然后，再对此洛朗级数的展开式的两端沿 $C$ 逐项积分：除了对 $c_{-1}(z-z_0)^{-1}$ 项的积分等于 $2\pi\text{i}c_{-1}$ 之外，其余项的积分都为零（由复合闭路定理及2.1节例题结论），即： $\displaystyle\oint_Cf(z)\mathrm{d}z=2\pi\text{i}c_{-1}$ 。

$\quad(3)$ 把（留下的）这个积分值除以 $2\pi\text{i}$ 后所得的数，称为函数 $f (z)$ 在 $z_0$ 的留数，记为 $\text{Res}[f(z),z_0]$ ，即

$\qquad\quad\text{Res}[f(z),z_0]=\dfrac{1}{2\pi\text{i}}\displaystyle\oint_Cf(z)\mathrm{d}z=c_{-1}$

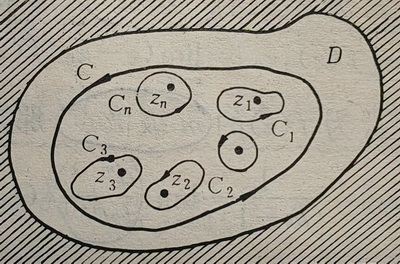
$\qquad$ 在这里插入图片描述

留数定理 设函数 $f (z)$ 在区域 $D$ 内除有限个孤立奇点 $z_1,z_2,\cdots,z_n$ 外处处解析， $C$ 是 $D$ 内包围各个奇点的一条正向简单闭曲线，那么
$\qquad\quad\displaystyle\oint_Cf(z)\mathrm{d}z=2\pi\text{i}\sum_{k=1}^n\text{Res}[f(z),z_k]$

证：在上图中，把在 $C$ 内的所有孤立奇点 $z_k$ 用互不包含的正向简单曲线 $C_k$ 包围起来
由复合闭路定理可得： $\displaystyle\oint_Cf(z)\mathrm{d}z=\displaystyle\oint_{C_1}f(z)\mathrm{d}z+\displaystyle\oint_{C_2}f(z)\mathrm{d}z+\cdots+\displaystyle\oint_{C_n}f(z)\mathrm{d}z$
两边都除以 $2\pi\text{i}$ ，可得 $\dfrac{1}{2\pi\text{i}}\displaystyle\oint_Cf(z)\mathrm{d}z=\text{Res}[f(z),z_1]+\text{Res}[f(z),z_2]+\cdots+\text{Res}[f(z),z_n]$

$\textcolor{red}{\bigstar}\quad$ 利用留数定理，求沿封闭曲线 $C$ 的积分，就转化为求被积函数在 $C$ 中的各孤立奇点处的留数。
　
$\bullet\quad$ 留数的计算规则

规则1 如果 $z_0$ 为 $f (z)$ 的一级极点，那么 $\text{Res}[f(z),z_0]=\displaystyle\lim_{z\to z_0}(z-z_0)f(z)$

规则2 如果 $z_0$ 为 $f (z)$ 的 $m$ 级极点，那么 $\text{Res}[f(z),z_0]=\dfrac{1}{(m-1)!}\displaystyle\lim_{z\to z_0}\textcolor{indianred}{\dfrac{\mathrm{d}^{m-1}}{\mathrm{d}z^{m-1}}\{(z-z_0)^mf(z)\}}$

证：由 $\textcolor{blue}{f(z)}=c_{-m}(z-z_0)^{-m}+\cdots+c_{-1}(z-z_0)^{-1}+c_0+c_{1}(z-z_0)+\cdots$
两边乘以 $z-z_0)^{m}$ 得到
　　 $\textcolor{blue}{(z-z_0)^{m}f(z)}=c_{-m}+c_{-m+1}(z-z_0)+\cdots+c_{-1}(z-z_0)^{m-1}+c_0(z-z_0)^{m}+\cdots$
两边求 $m - 1$ 阶导数，得 $\dfrac{\mathrm{d}^{m-1}}{\mathrm{d}z^{m-1}}\{(z-z_0)^mf(z)\}=(m-1)!c_{-1}+\{$ 含有 $z-z_0$ 正幂的项 $\}$
令 $z\to z_0$ 两端求极限， $\displaystyle\lim_{z\to z_0}\textcolor{blue}{\dfrac{\mathrm{d}^{m-1}}{\mathrm{d}z^{m-1}}\{(z-z_0)^mf(z)\}}=(m-1)!\textcolor{crimson}{c_{-1}}$
可得 $\text{Res}[f(z),z_0]=\dfrac{1}{2\pi\text{i}}\displaystyle\oint_Cf(z)\mathrm{d}z=\textcolor{crimson}{c_{-1}}=\dfrac{1}{(m-1)!}\displaystyle\lim_{z\to z_0}\textcolor{blue}{\dfrac{\mathrm{d}^{m-1}}{\mathrm{d}z^{m-1}}\{(z-z_0)^mf(z)\}}$

规则3 设 $f(z)=\dfrac{P(z)}{Q(z)}$ ， $P (z)$ 和 $Q (z)$ 在 $z_0$ 都解析，如果 $P(z_0)\neq0$ ， $Q(z_0)=0$ ， $Q^\prime(z_0)\neq0$
　　　那么 $z_0$ 为 $f (z)$ 的一级极点，且 $\text{Res}[f(z),z_0]=\dfrac{P(z_0)}{Q^\prime(z_0)}$

例. 计算积分 $\displaystyle\oint_C\dfrac{ze^z}{z^2-1}\mathrm{d}z$ ， $C$ 为正向圆周： $∣ z ∣ = 2$
由于 $f (z)$ 有两个一级极点 $+ 1, - 1$ ，且极点都在 $C$ 内，由规则1
$\begin{aligned}\displaystyle\oint_C\dfrac{ze^z}{z^2-1}\mathrm{d}z&=2\pi\text{i}\{\ \text{Res}[f(z),+1]+\text{Res}[f(z),-1]\ \} \\ &=2\pi\text{i}\{\ \lim_{z\to 1}(z-1)\dfrac{ze^z}{z^2-1} +\lim_{z\to -1}(z+1)\dfrac{ze^z}{z^2-1}\} \\ &=2\pi\text{i}\{\ \lim_{z\to 1}\dfrac{ze^z}{z+1} +\lim_{z\to -1}\dfrac{ze^z}{z-1} \} \\ &=\pi\text{i}(e+e^{-1}) \end{aligned}$
或者由规则3
$\begin{aligned}\displaystyle\oint_C\dfrac{ze^z}{z^2-1}\mathrm{d}z&=2\pi\text{i}\{\ \text{Res}[f(z),+1]+\text{Res}[f(z),-1]\ \} \\ &=2\pi\text{i}\{\ \dfrac{ze^z}{2z}\big|_{z=+1} +\dfrac{ze^z}{2z}\big|_{z=-1}\} \\ &=\pi\text{i}(e+e^{-1}) \end{aligned}$

例. 计算积分 $\displaystyle\oint_C\dfrac{e^z}{z(z-1)^2}\mathrm{d}z$ ， $C$ 为正向圆周： $∣ z ∣ = 2$
由于 $f (z)$ 有一级极点 $z = 0$ ，有二级极点 $z = 1$ ，且极点都在 $C$ 内，由规则1和规则2
$\begin{aligned}\displaystyle\oint_C\dfrac{ze^z}{z^2-1}\mathrm{d}z&=2\pi\text{i}\{\ \text{Res}[f(z),0]+\text{Res}[f(z),1]\ \} \\ &=2\pi\text{i}\{\ \lim_{z\to 0}z\dfrac{e^z}{z(z-1)^2} +\lim_{z\to 1}\dfrac{\mathrm{d}}{\mathrm{d}z}\{(z-1)^2\dfrac{e^z}{z(z-1)^2}\}\} \\ &=2\pi\text{i}\{\ 1 +\lim_{z\to 1}\dfrac{\mathrm{d}}{\mathrm{d}z}\{\dfrac{e^z}{z}\} \} \\ &=2\pi\text{i}(\ 1 +\lim_{z\to 1}\dfrac{e^zz-e^z}{z^2} ) \\ &=2\pi\text{i} \end{aligned}$
　
$\bullet\quad$ 在无穷远点的留数

定义 设函数 $f (x)$ 在圆环域 $R<|z|<+\infty$ 内解析， $C$ 为圆环域内绕原点的任何一条正向简单闭曲线，那么 $\dfrac{1}{2\pi\text{i}}\displaystyle\oint_{C^-}f(z)\mathrm{d}z$ 的值与 $C$ 无关，称此定值为 $f (x)$ 在无穷远点 $\infty$ 的留数，记作 $\text{Res}[f(z),\infty]=\dfrac{1}{2\pi\text{i}}\displaystyle\oint_{C^-}f(z)\mathrm{d}z$ 。

在5.3中， $f (x)$ 在圆环域 $R<|z|<+\infty$ 内解析，在该圆环域内的洛朗级数展开式为（ $C$ 为该圆环域内绕原点的任何一条正向简单闭曲线）：
$\qquad\quad\begin{aligned}f(z)&=\sum_{n=1}^\infty c_{-n}z^{-n}+c_0+\sum_{n=1}^\infty c_nz^n \ , \ c_n=\dfrac{1}{2\pi\text{i}}\displaystyle\oint_C\dfrac{f(\zeta)}{\zeta^{n+1}}\mathrm{d}\zeta\ \ (n=0,\pm1,\pm2,\cdots) \end{aligned}$

$\quad$ 显然，当 $n = - 1$ 时， $c_{-1}=\dfrac{1}{2\pi\text{i}}\displaystyle\oint_Cf(\zeta)\mathrm{d}\zeta$ 。
$\quad$ 因此， $f (x)$ 在无穷远点 $\infty$ 的留数 $\text{Res}[f(z),\infty]=-c_{-1}$ 。
　
定理 如果函数 $f (z)$ 在扩充复平面内只有有限个孤立奇点，那么 $f (z)$ 在所有各奇点（包括无穷远点 $\infty$ ）的留数的总和必等于零。

除无穷远点 $\infty$ 之外，设 $f (z)$ 的有限个奇点为 $z_k(k=1,\cdots,n)$ ，又设 $C$ 为一条绕原点的、并将 $z_k(k=1,\cdots,n)$ 包含在内部的正向简单闭曲线。
根据留数定理 $\displaystyle\oint_Cf(z)\mathrm{d}z=2\pi\text{i}\ \sum_{k=1}^n\text{Res}[f(z),z_k]$
以及无穷远点的留数定义 $\displaystyle\oint_{C^-}f(z)\mathrm{d}z=2\pi\text{i}\ \text{Res}[f(z),\infty]$
因此 $\text{Res}[f(z),\infty]+\displaystyle\sum_{k=1}^n\text{Res}[f(z),z_k]=\dfrac{1}{2\pi\text{i}}\displaystyle\oint_{C^-}f(z)\mathrm{d}z+\dfrac{1}{2\pi\text{i}}\displaystyle\oint_Cf(z)\mathrm{d}z=0$

规则4 关于无穷远点的留数计算，有 $\text{Res}[f(z),\infty]=-\text{Res}\left[f\left(\dfrac{1}{z}\right)\dfrac{1}{z^2},0\right]$

例. 计算积分 $\displaystyle\oint_C\dfrac{z}{z^4-1}\mathrm{d}z$ ， $C$ 为正向圆周： $∣ z ∣ = 2$
由于 $f (z)$ 在 $∣ z ∣ = 2$ 的外部，除了无穷远点 $\infty$ 之外，没有其他奇点，由本节定理和规则4
$\begin{aligned}\displaystyle\oint_C\dfrac{z}{z^4-1}\mathrm{d}z&=-2\pi\text{i}\ \text{Res}[f(z),\infty] \\ &=2\pi\text{i}\ \text{Res}\left[f\left(\dfrac{1}{z}\right)\dfrac{1}{z^2},0\right] \\ &=2\pi\text{i}\ \text{Res}\left[\dfrac{z}{1-z^4},0\right]=0 \end{aligned}$

复变函数摘记3

5. 留数

5.1 可去奇点、极点、本性奇点

5.2 零点与极点的关系

5.3 在无穷远点处的情形

5.4 留数

相关文章：