当前位置：首页 > news >正文

二叉树 --- 堆(下）

news 来源：原创 2025/9/6 21:56:14

今天我们来把堆完结了。

对于一个高度为 h 的满二叉树，有

F(h) = 2 ^ 0 + 2 ^ 1 + …… + 2 ^ (h - 1) = 2 ^ h - 1 h = log2 (N+1)

对于一个高度为 h 的完全二叉树，且最后一层只有一个，则

F(h) = 2 ^ 0 + 2 ^ 1 + …… + 2 ^ (h - 2) + 1 = 2 ^ (h -1) h = log2 N + 1

所以对于向上调整或向下调整算法，每次最多是调整 log2 N 次

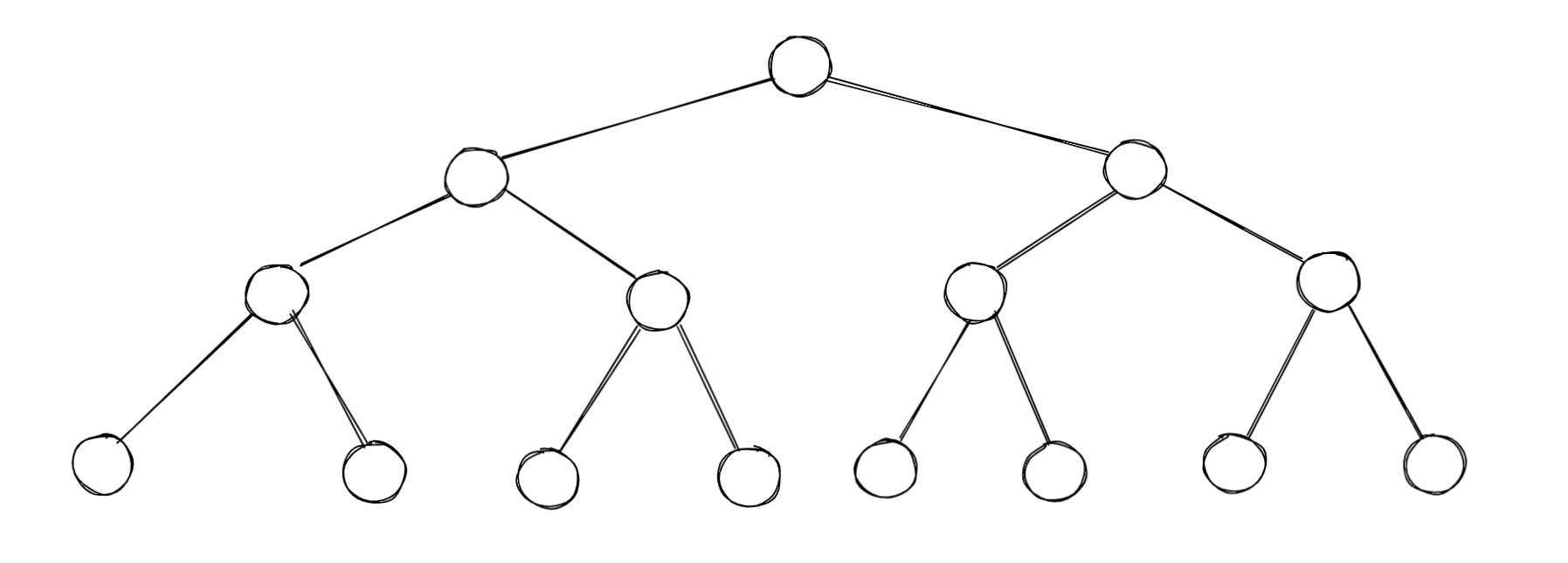
对于一个满二叉树

第 1 层有 2 ^ 0 个节点，最坏的情况向下调整要调整 h - 1 次

第 2 层有 2 ^ 1 个节点，最坏的情况向下调整要调整 h - 2 次

……

第 h - 1 层有 2 ^ (h - 2) 个节点，最坏的情况向下调整要调整 1 次

第 h 层有 2 ^ (h - 1) 个节点，最坏的情况向下调整要调整 0 次

所以我们可以得到完全二叉树的时间复杂度函数为

T(h) = 2 ^ 0 * ( h - 1 ) + 2 ^ 1 * ( h - 2 ) + …… + 2 ^ ( h - 2 ) * 1 + 2 ^ ( h - 1 ) * 0

使用错位相减法后得

T(h) = 2 ^ 1 + 2 ^ 2 + …… + 2 ^ (h - 2) 1 - 2 ^ 0 * (h -1) = 2 ^ 1 + 2 ^ 2 + …… + 2 ^ (h - 2) * 1 + 2 ^ 0 - 2 ^ 0 * (h - 1)

一个高度为 h 的满二叉树节点个数为 N，则有 2 ^ h - 1 = N

用等比数列公式进行化简可得，T(h) = 2 ^ h - 1 - h

由于高度我们一般不是很敏感，所以用 N 代替

T(N) = N - log2 (N + 2) 则向下调整算法的时间复杂度为 O(N)

第 1 层有 2 ^ 0 个节点，最坏的情况向上调整要调整 0 次

第 2 层有 2 ^ 1 个节点，最坏的情况向上调整要调整 1 次

……

第 h - 1 层有 2 ^ (h - 2) 个节点，最坏的情况向上调整要调整 h - 2 次

第 h 层有 2 ^ (h - 1) 个节点，最坏的情况向下调整要调整 h - 1 次

T(h) = 2 ^ 1 * 1 + 2 ^ 2 * 2 + …… + 2 ^ (h - 2) * (h - 2) + 2 ^ (h - 1) * (h - 1)

依然用错位相减法可得：

T(N) = - N + (N + 1) * (log2 (N + 1) - 1) + 1

则向上调整算法的时间复杂度为 O(N * log2 N)

节点少的数乘以调整数小的数，节点多的数乘以调整数大的数，时间复杂度必然大

所以说向下调整算法建堆是比向上调整算法建堆要优化的多

我们现在有向下调整算法了，我们就可以重新写一下堆排序

void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}

Top K 问题

N 个数中找最大的前 K 个

方法1：

建一个 N 个数的大堆 O( N )
Pop K次 O(K * log2 N)

但是，这里有个很致命的问题，假设 N 特别大，需要多少内存呢？

N 为 10 亿的时候，大概需要消耗 3.78G 的内存，这实在是太耗空间了

如果我只给你 1kb个内存空间呢，那我们不可能把所有数全部都保存起来。所以要换一种思路

方法2：

用前 k 个数，建一个小堆 O(K)
剩下的数据跟堆顶的数据进行比较，如果比堆顶的数据大，就替代堆顶进堆（覆盖根节点位置，然后向下调整） O((N - K) * (log2 K)
最后这个小堆就是最大的前 k 个

所以合计效率依然是 O(N)

接下来，我们开始写代码：

首先我们先来造10000个随机的数据

#include <time.h>
void CreateDate()
{//造数据int n = 10000;srand(time(0));const char* file = "date.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error!");return;}for (int i = 0; i < n; i++){int date = rand() + i;fprintf(fin, "%d\n", date);}fclose(fin);
}

然后我们写代码找到最大的 k 个数

void test2()
{int k;scanf("%d", &k);int* kminheap = (int*)malloc(sizeof(int) * k);if (kminheap == NULL){perror("malloc failed!");return;}const char* file = "date.txt";FILE* fout = fopen(file, "r");//读取文件中前 k 个数for (int i = 0; i < k; i++){fscanf(fout, "%d", &kminheap[i]);}//建 k 个数的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminheap, k, i);}//读取剩下的 N - k 个数int x = 0;while (fscanf(fout, "%d", &x) > 0){if (x > kminheap[0]){kminheap[0] = x;AdjustDown(kminheap, k, 0);}}//打印前十个数printf("\n最大的前%d个数是： ", k);for (int i = 0; i < k; i++){printf("%d ", kminheap[i]);}
}

现在我们写好代码了，代码也成功跑起来了，在控制台也找出来了10个数，这10个数到底是不是最大的呢？我们该怎么检查

我们去一个一个比对嘛？不用的，我们从数据入手

int date = (rand() + i) % 1000000;

我们先将随机生成的数据规定在 1000000 以内，然后手动到数据库中修改 10 个数据，把这几个数变大，超过 1000000，然后再运行程序，看代码找出来的数是否是我们修改后的那几个大数即可

这个测试方法也称为打锚点

到此，堆章节我们就讲完了！

二叉树 --- 堆(下）

今天我们来把堆完结了。对于一个高度为 h 的满二叉树，有 F(h) 2 ^ 0 2 ^ 1 …… 2 ^ (h - 1) 2 ^ h - 1 h log2 (N1) 对于一个高度为 h 的完全二叉树，且最后一层只有一个 ，则 F(h) 2 ^ 0 2 ^ 1 …… 2 ^ (h - 2) 1 2 ^ (h -…...

编程日记 2025/9/6 21:56:14

数组对象[object]，五种如何去重方法 js

前言数组有很多方法都可以实现去重。本章分享比较常用的。准备工作准备一组数组对象 let arr [{ id: "1", name: "张晓", age: 14 },{ id: "2", name: "张晓", age: 14 },{ id: "3", name: "张晓", age: 1…...

编程日记 2025/9/6 21:46:52

PyRoboPlan 库，给 panda 机械臂微分 IK 上大分，关节限位、碰撞全不怕

视频讲解： PyRoboPlan 库，给 panda 机械臂微分 IK 上大分，关节限位、碰撞全不怕代码仓库：https://github.com/LitchiCheng/mujoco-learning 今天分享PyRoboPlan库，比之前的方式优点在于，这个库考虑了机械…...

编程日记 2025/9/6 21:49:31

【模态分解】EMD-经验模态分解

算法配置页面，也可以一键导出结果数据报表自定义绘制获取和下载【PHM学习软件PHM源码】的方式获取方式：Docshttps://jcn362s9p4t8.feishu.cn/wiki/A0NXwPxY3ie1cGkOy08cru6vnvc...

编程日记 2025/8/17 19:08:32

文章目录前言一、服务端新增/修改规则1.1、repository.save1.2、publishRules 二、客户端接收规则三、持久化扩展3.1、持久化原理3.1.1、FileRefreshableDataSource3.1.1.1、super关键字3.1.1.2、firstLoad()方法 3.1.2、FlowRuleManager.register2Property 3.2、持久化实现总…...

编程日记 2025/9/6 11:25:27

【go】--编译

go build -o [编译完成的可执行文件] [需要编译的.go文件]#例如 go build -o myapp main.go#确保编译的结果和当前运行环境相同 #查看arch uname -a在 Linux 中查看和修改 GOOS 和 GOARCH 环境变量： 1. 查看当前 Go 环境变量 # 查看所有Go相关的环境变量 go env# …...

编程日记 2025/9/2 13:31:33

【Spring底层分析】Spring IoC

Spring IoC IoC：控制反转。将对象创建和对象之间的调用交给Spring容器来管理。好处是降低了对象之间的耦合度。 DI：依赖注入。给bean对象注入依赖的对象。大白话就是：Spring帮你创建对象，对象的属性如果依赖于某个对象&#xf…...

编程日记 2025/9/4 13:57:01

Ubuntu系统进程管理

在Ubuntu系统中，进程管理是系统维护和性能调优的重要部分。以下是关键命令和技巧的总结，帮助你有效管理系统进程： 1. 查看进程 ps 命令：查看当前进程快照。 bash ps aux # 查看所有运行中的进程（a所有用户…...

编程日记 2025/9/6 0:45:13

HDU2196 Computer 树形DP

原题链接既然要查找每个节点的最远到达距离，由于该图是个树，我们就找从根节点向下遍历方向的终点的距离与先返回父节点再从最优的父节点沿着原来的方向的终点的距离的最大值如图所示也就是说，我们需要获得当前点的正距离最大值和正距离最…...

编程日记 2025/9/3 7:32:05

【第四十周】文献阅读：用于检索-增强大语言模型的查询与重写

目录摘要Abstract用于检索-增强大语言模型的查询与重写研究背景方法论基于冻结LLM的重写方案基于可训练重写器的方案重写器预热训练（Rewriter Warm-up）强化学习（Reinforcement Learning） 创新性实验结果局限性总结摘要这篇论文…...

编程日记 2025/9/6 1:22:34

Istio常用命令

Istio常用命令 1. 安装和配置2. Sidecar 注入3. 验证和状态4. 升级和卸载5. 故障排除6. 配置管理 istioctl 的常用命令及其详细说明： 1. 安装和配置安装 Istio # 使用指定的配置文件（如 demo）安装 Istio 到 Kubernetes 集群。 istioctl m…...

编程日记 2025/9/3 22:59:14

Linux基础15

一、网络模型二、eNSP模拟器拖拽操作建立模拟网络环境交换机视图操作： <> 用户视图 [] 系统视图接口视图协议视图 display version #显示版本和设备型号 display current-configuration #查看设备配置(查错) …...

编程日记 2025/9/3 4:35:19

FISCO BCOS群组扩容实战指南：从原理到操作全解析

引言：为什么需要群组扩容？ 在区块链技术迅猛发展的今天，企业级应用对区块链平台提出了更高的要求。"如何在不影响现有业务的情况下扩展区块链处理能力？"、"能否实现不同业务数据的物理隔离？"、&qu…...

编程日记 2025/9/2 14:48:44

【pytorch图像视觉】lesson17深度视觉应用（上）构建自己的深度视觉项目

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、数据1、认识经典数据1.1入门数据：MNIST、其他数字与字母识别（1）数据加载（2）查看数据的特征和标…...

编程日记 2025/9/4 8:29:23

从“被动跳闸”到“主动预警”：智慧用电系统守护老旧小区安全

安科瑞顾强近年来，老旧小区电气火灾事故频发，成为威胁居民生命财产安全的重要隐患。据统计，我国居住场所火灾伤亡人数远超其他场所，仅今年一季度就发生8.3万起住宅火灾，造成503人遇难。这些建筑多建于上世纪&#x…...

编程日记 2025/9/5 12:16:05

2.1 全栈运维管理：Proxmox VE单节点配置桥接、VLAN和Bonding的详细实验指南

本文是Proxmox VE 全栈管理体系的系列文章之一，如果对 Proxmox VE 全栈管理感兴趣，可以关注“Proxmox VE 全栈管理”专栏，后续文章将围绕该体系，从多个维度深入展开。概要：本文介绍 Proxmox VE 单节点网络配置。桥接基…...

编程日记 2025/9/6 7:48:44

docker面试题

1.docker网络 Docker网络是Docker容器之间进行通信的关键功能。Docker提供了多种网络模式和驱动，以满足不同的网络需求。以下是Docker网络的详细介绍： 1.Docker网络模式 Docker提供了以下几种网络模式，每种模式适用于不同的场景：…...

编程日记 2025/8/19 9:33:28

计算机视觉——基于YOLOV8 的人体姿态估计训练与推理

概述自 Ultralytics 发布 YOLOV5 之后，YOLO 的应用方向和使用方式变得更加多样化且简单易用。从图像分类、目标检测、图像分割、目标跟踪到关键点检测，YOLO 几乎涵盖了计算机视觉的各个领域，似乎已经成为计算机视觉领域的“万能工具”。 Y…...

编程日记 2025/9/4 20:57:26

【本地图床搭建】宝塔+Docker+MinIO+PicGo+cpolar：打造本地化“黑科技”图床方案

写在前面：本博客仅作记录学习之用，部分图片来自网络，如需引用请注明出处，同时如有侵犯您的权益，请联系删除！ 文章目录前言宝塔安装DockerMinIO 安装与设置cploar内网穿透PicGo下载与安装typora安装总结互动…...

编程日记 2025/9/3 2:05:38

【家政平台开发(41)】家政平台性能蜕变：性能测试与优化全解析

本【家政平台开发】专栏聚焦家政平台从 0 到 1 的全流程打造。从前期需求分析，剖析家政行业现状、挖掘用户需求与梳理功能要点，到系统设计阶段的架构选型、数据库构建，再到开发阶段各模块逐一实现。涵盖移动与 PC 端设计、接口开发及性能优化，测试阶段多维度保障平台质量，…...

编程日记 2025/8/28 22:31:13

监控docker中的java应用

1)进入指定的容器 docker exec -it demo /bin/bash 2)下载curl root89a67e345354:/# apt install curl -y 3)下载arthas root89a67e345354:/# curl -O https://arthas.aliyun.com/arthas-boot.jar 4)运行 root89a67e345354:/# java -jar arthas-boot.jar 5)监控 […...

编程日记 2025/8/29 6:02:49

Android游戏辅助工具开发详解

文章目录第一部分：概述与基础准备1.1 游戏辅助工具的定义与用途1.2 开发环境准备1.3 项目创建与配置第二部分：核心功能实现2.1 屏幕点击功能实现2.1.1 基础点击功能2.1.2 多点触控实现 2.2 滑动功能实现2.2.1 基础滑动功能2.2.2 曲线滑动实现 2.3 屏幕…...

编程日记 2025/9/1 0:38:10

重生之外卖配送时被投诉后的反思

重生之外卖配送时被投诉后的反思写苍穹外卖时我们发现在每一次调用sql语句时 insert update语句总会需要在service的实现类里加入例如create_time,create_user , update_time , update_user的填充每次赋值都要重新编写代码，会造成代码冗余 ； 序号字…...

编程日记 2025/9/2 8:47:37

计算机基础复习资料整理

计算机基础复习资料整理一、操作系统 （一）定义操作系统（Operating System，OS）是介于计算机硬件和用户（程序或人）之间的接口。作为通用管理程序，它管理计算机系统中每个部件的活动…...

编程日记 2025/9/6 4:19:28

Profibus DP主站网关数据映射全解析！

Profibus DP主站网关数据映射全解析！ 在工业自动化领域，Profibus DP主站网关作为一种关键的通讯设备，其数据映射的精准度和效率对整个控制系统的性能有着至关重要的影响。本文旨在深入探讨Profibus DP主站网关的数据映射过程，揭示…...

编程日记 2025/9/2 21:04:01

ocr-不动产权识别

目录一、在阿里云申请ocr识别服务二、创建springboot项目三、后续一、在阿里云申请ocr识别服务在线体验：房产证图片上传 [阿里官方]不动产权证OCR文字识别_API专区_云市场-阿里云 (aliyun.com) 可以选择一毛500次这个当然也可以白嫖100 下面有个在线调试…...

编程日记 2025/9/5 3:52:36

leetcode 198. House Robber

本题是动态规划问题。第一步，明确并理解dp数组以及下标的含义 dp[i]表示从第0号房间一直到第i号房间(包含第i号房间)可以偷到的最大金额，具体怎么偷这里不考虑，第i1号及之后的房间也不考虑。换句话说，dp[i]也就是只考虑[0,i]号…...

编程日记 2025/8/31 11:13:07

【2025软考高级架构师】——软件架构设计（4）

摘要本文主要介绍了几种软件架构设计相关的概念和方法。包括C2架构风格的规则，模型驱动架构（MDA）的起源、目标、核心模型及各模型之间的关系；软件架构复用的概念、历史发展、维度、类型及相关过程；特定领域架构&…...

编程日记 2025/9/4 14:29:10

分发饼干问题——用贪心算法解决

目录一：问题描述二：解决思路贪心策略（C语言）算法复习总结3——贪心算法-CSDN博客三：代码实现四：复杂度分析一：问题描述分发饼干问题是一个经典的可以使用贪心算法解决的问题&#xf…...

编程日记 2025/9/1 10:01:04

深入详解MYSQL的MVCC机制

参考资料：参考视频（注意第二个视频关于幻读的讲解是错误的，详情见本文） redoLog的结构详解参考资料学习内容： 1. MVCC要解决的问题 MVCC要解决的问题是，在不产生脏读等数据库问题的前提下，数据库的查询语句和更改语句不相互阻塞的情况；在InnoDB中，MVCC仅仅存…...

编程日记 2025/9/6 8:01:48

DNS域名解析

目录一.DNS 1.1DNS的简介 1.2DNS的背景 1.3DNS的架构 1.4实现DNS的方式 1.5DNS的查询类型 1.6DNS解析的基本流程二.主从复制 2.1定义 2.2优缺点三.DNS服务软件 3.1bind 3.1.1定义 3.1.2bind相关文件 3.2DNS服务器的核心文件 3.2.1主配置文件 3.2.2域名文件 …...

编程日记 2025/9/6 7:30:41

Java基础：一文讲清多线程和线程池和线程同步

01-概述 02-线程创建继承Thread 实现Runnable(任务对象) 实现Callable接口 public class ThreadDemo3 {public static void main(String[] args) throws ExecutionException, InterruptedException {// 目标：线程创建3// 需求：求1-100的和Callable<…...

编程日记 2025/9/4 0:12:05

ubuntu 20.04 连不上蓝牙耳机/蓝牙鼠标

sudo gedit /etc/bluetooth/main.conf改为 ControllerMode dual然后重启蓝牙服务 sudo service bluetooth restart...

编程日记 2025/8/17 21:05:26

SaaS、Paas、IaaS、MaaS、BaaS五大云计算服务模式

科普版：通俗理解五大云计算服务模式 1. SaaS（软件即服务） 一句话解释：像“租用公寓”，直接使用现成的软件，无需操心维护。案例：使用钉钉办公、在网页版WPS编辑文档。服务提供商负责软件更新和…...

编程日记 2025/9/5 3:09:23

【深拷贝、浅拷贝】golang函数参数传递，变量复制后，操作变量参数，是否影响原有数据？全面解析

Golang中深拷贝与浅拷贝的详细解析，以及变量复制、函数参数传递等场景下对新旧变量影响的总结： 一拷贝与浅拷贝的核心区别 1. 浅拷贝（Shallow Copy） • 定义：仅复制数据的顶层结构，对引用类型字段&#x…...

编程日记 2025/9/2 17:15:41

c语言编程经典习题详解3

21. 求给定正整数 n 以内的素数之积定义：找出小于给定正整数n的所有素数，并将它们相乘。要点：使用双层for循环，外层循环遍历小于n的数，内层循环判断是否为素数，若是则累乘。应用：在数论研究、密码学等领域有应用。c #include <stdio.h>int isPrime(int num) {if…...

编程日记 2025/8/31 10:59:08

【HD-RK3576-PI】Docker搭建与使用

硬件：HD-RK3576-PI 软件：Linux6.1Ubuntu22.04 1. 安装Docker Docker安装脚本下载： roothd-rk3576-pi:~ $ curl -fsSL https://test.docker.com -o test-docker.sh 可以直接执行安装 roothd-rk3576-pi:~ $ sh test-docker.sh 2. 配置国内镜…...

编程日记 2025/9/5 5:24:44

C++进阶——异常

目录 1、异常的概念及使用 1.1 异常的概念 1.2 异常的抛出和捕获 1.3 栈展开 1.4 查找匹配的处理代码 1.5 异常的重新抛出 1.6 异常的安全问题 1.7 异常的规范 2、标准库的异常(了解) 1、异常的概念及使用 1.1 异常的概念 C语言，出错了，就报错…...

编程日记 2025/8/20 7:38:06

Linux安装开源版MQTT Broker——EMQX服务器环境从零到一的详细搭建教程

零、EMQX各个版本的区别 EMQX各个版本的功能对比详情https://docs.emqx.com/zh/emqx/latest/getting-started/feature-comparison.html...

编程日记 2025/8/17 19:08:34

C++ 编程指南36 - 使用Pimpl模式实现稳定的ABI接口

一：概述 C 的类布局（尤其是私有成员变量）直接影响它的 ABI（应用二进制接口）。如果你在类中添加或修改了私有成员，即使接口不变，编译器生成的二进制布局也会变，从而导致 ABI 不兼容。…...

编程日记 2025/8/29 17:49:01

笔记本电脑突然无法开机电源灯亮但是屏幕无法点亮

现象按电源键，电源灯点亮，屏幕没动静风扇开始运转，然后一会儿就不转了；屏幕一直没动静，屏幕没有任何反应（没有系统启动画面，没有徽标显示，就一点反应也没用） 这个问…...

编程日记 2025/9/5 7:08:19

mongodb 4.0+多文档事务的实现原理

1. 副本集事务实现（4.0）‌ ‌非严格依赖二阶段提交‌ MongoDB 4.0 在副本集环境中通过 ‌全局逻辑时钟（Logical Clock）‌ 和 ‌快照隔离（Snapshot Isolation）‌ 实现多文档事务，事务提交时通过…...

编程日记 2025/9/5 14:48:19

decompiled.class file bytecode version50(java 6)

idea运行项目报错，跳到具体的.class中，idea会给出提示下载源码，点击下载报错，具体报错信息我没记录了（反正就是无法看到源码） 解决方式： 1、网上说下载scala插件，重启idea即可但是…...

编程日记 2025/9/1 13:44:33

CSS 列表样式学习笔记

CSS 列表样式提供了强大的功能，用于定制 HTML 列表的外观。通过 CSS，可以轻松地改变列表项的标记类型、位置，甚至使用图像作为列表项标记。以下是对 CSS 列表样式的详细学习笔记。一、HTML 列表类型在 HTML 中，主要有两种类型…...

编程日记 2025/9/3 0:42:24

linux网络设置

ifconfig 查看ip地址查看当前的liunx系统的网络参数ip地址 Ubuntu需要安装 Apt install -y net-tools 查看网络信息 Ifconfig 只能看到开启的网卡 Ifconfig -a 看到所有的网卡包括开启和关闭的 Ifconfig 网卡名称 up 开启网卡 Ifconfig 网卡名称 down 关闭网卡 If…...

编程日记 2025/8/27 4:50:54

抗干扰CAN总线通信技术在分布式电力系统中的应用

摘要：随着分布式电力系统的广泛应用，其通信系统的可靠性与稳定性受到了前所未有的挑战。CAN总线通信技术以其卓越的抗干扰性能和可靠性，在众多通信技术中脱颖而出，成为解决分布式电力系统通信问题的关键。本文深入剖析了CAN总线通…...

编程日记 2025/9/1 21:57:45

Maven工具学习使用（十二）——extension和depency的区别

在 Maven 中，extensions 和 dependencies 是两个不同的概念，它们在项目构建和依赖管理中扮演着不同的角色。 1、Dependencies dependencies 是 Maven 项目中用于管理项目所需的库和模块的部分。这些依赖可以是本地仓库中的，也可以是远程仓库…...

编程日记 2025/9/4 11:55:10

Python学生信息查询

利用字典设置学生信息，将这些信息放入列表中进行存储，根据输入的姓名查询展示对应的学生信息。 Student1{no:202001,name:zyt,score:87} Student2Student1.copy() Student3Student2.copy()Student2[no]202002 Student3[no]202003Student2[name]zwh Stud…...

编程日记 2025/9/5 11:22:21

一天时间，我用AI(deepseek)做了一个配色网站

前言最近在开发颜色搭配主题的相关H5和小程序，想到需要补充一个web网站，因此有了这篇文章。一、确定需求向AI要答案之前，一定要清楚自己想要做什么。如果你没有100%了解自己的需求，可以先让AI帮你理清逻辑和思路，…...

编程日记 2025/8/31 15:38:52

MQ（消息队列）体系详解

消息队列（MQ，Message Queue） 是一种基于消息传递的异步通信机制，用于不同系统、服务之间进行数据传递和交互。它通常用来解耦生产者和消费者，提供高可用、高吞吐量和可靠的消息传递。一、消息队列用途 1.系统解耦 …...

编程日记 2025/9/5 1:47:33

相关文章：