当前位置： 首页 > news >正文

【算法】快速排序

news 来源：原创 2025/9/13 7:08:49

算法系列六：快速排序

一、快速排序的递归探寻

1.思路

2.书写

3.搭建

3.1设计过掉不符情况（在最底层时）

3.2查验能实现基础结果（在最底层往上点时）

3.3跳转结果继续往上回搭

4.实质

二、快速排序里的基准排序

1.双路双向交换铺（Hoare法）

1.1原理

1.2实现

1.2.1>=

1.2.2先右再左

2.双路双向覆盖铺（挖坑法）

2.1原理

2.2实现

3.双路单向交换铺（前后指针法）

3.1原理

3.2实现

三、快速排序的复杂度

1.时间复杂度

1.1完全顺序逆序

1.1.1结构影响

1.1.2时间

1.2完全二叉树序

1.2.1结构影响

1.2.2时间

2.空间复杂度

3.优化

3.1三数取中

3.2插入排序

3.2.1栈溢出原因

3.2.2利与弊

 

一、快速排序的递归探寻

1.思路

左断开结果与右断开结果加上突兀根如何实现上一层的结果：

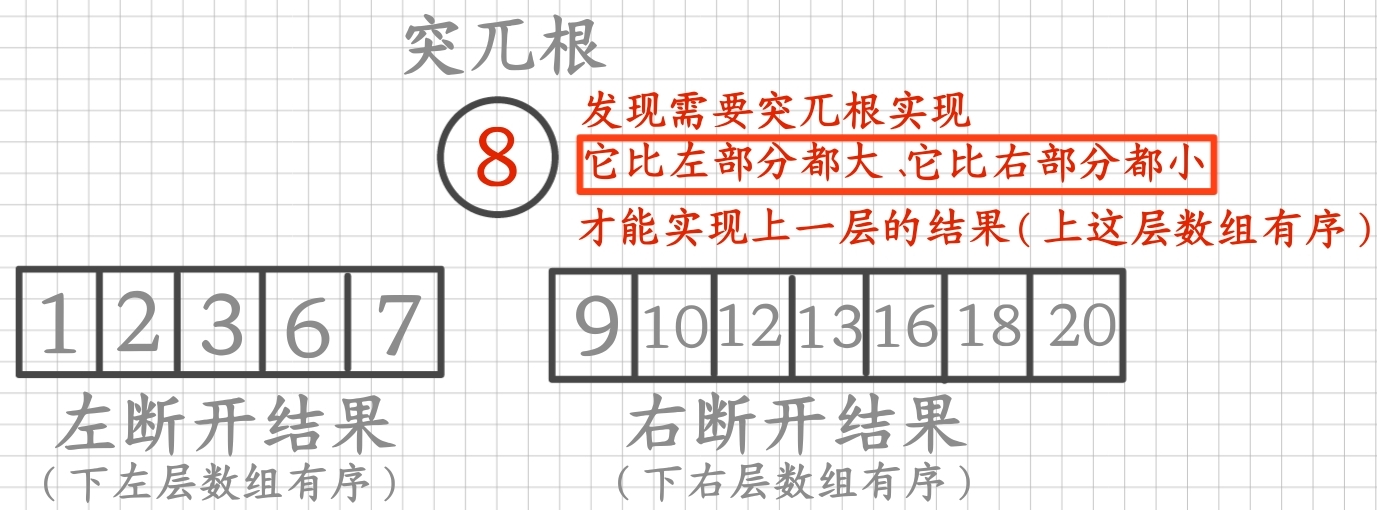
左断开有序+右断开有序加突兀根实现它比左部分都大、它比右部分都小就可以实现上一层的有序

2.书写

书写时是突兀根先实现再递归实现左右断开结果：

书写时反着来先实现突兀根一个节点左边都比都比它小、右边都比它大，再用递归实现它断开的左右有序结果

3.搭建

突兀根从底层向上的回搭搭建二叉树：

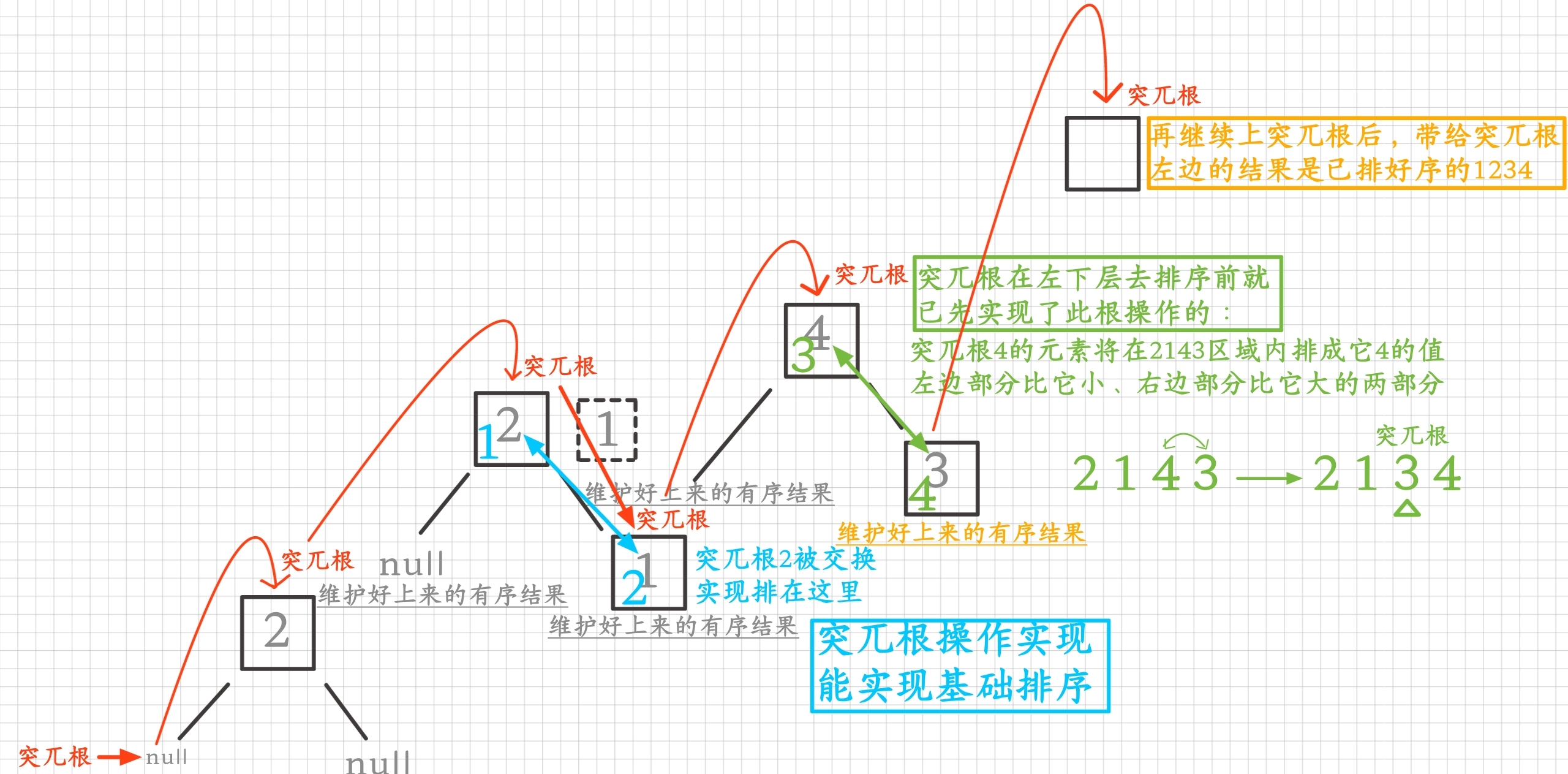
3.1设计过掉不符情况（在最底层时）

  • if(array == null) return， 没有元素不用排，下面是有元素
  • if(strat == end) return，只有一个元素不用排，下面是多个元素
  • if(strat > end) return，排不了不要排的，之后下面是符合正常情况的多个元素 

3.2查验能实现基础结果（在最底层往上点时）

当突兀根来到倒数第二层，当共有两个元素下突兀根去作为在上层的会去操作实现上层与下两层结果的表示连接时，左边、右边都是有序的结果，要实现它这层的有序结果要突兀根去操作实现为它的值比左边的都大、比右边的都小，操作具体实现为与1节点的值进行交换完成突兀根的实现操作，实现了突兀根所在的上层结果与下层左右两断开结果的连接表示，说明突兀根的实现操作在底层确实是能完成基础排序的

3.3跳转结果继续往上回搭

4.实质

用二叉树递归实现排序实质上还是确定元素大小排在的数组位置递归完一个个来排的：

它排的位置左边都比它小、右边都比它大，它排的位置就是它在数组中排的大小位置，同时也确定着其它元素的相对大小排位位置，所以最后一层元素不去找基准排位置也是相对已确定下来的不用去排，所以if(start == end)return的

二、快速排序的基准排序

待排序元素将其所在的待排序区域调整划分成以它为基准值左边都比它小、右边都比它大的两部分，并将它基准值放入两部分的中间就完成了此元素的排序

1.双路双向交换铺（Hoare法）

1.1原理

要去排的元素基准值在待排序区域里面任意取好后，在待排序区域左右两端往内相遇铺路，右端往内铺遇小不符等停，左端往内铺遇大换过去交换，直至路头遇相等，此时路头位置即基准元素大小排在的位置，最后将基准元素交换过去就完成了此元素的排序

1.2实现

private static int partition(int[] array, int left, int right) {int i = left;int j = right;int pivot = array[left];while (i < j) {while (i < j && array[j] >= pivot) {j--;}while (i < j && array[i] <= pivot) {i++;}swap(array, i, j);}swap(array, i, left);return i;}
1.2.1>=

遇到与基准值相等大小的元素时直接作为可行的路过掉的因为与基准值相等大小的元素到最后排序在此作为基准元素左右两边都是可以的，所以此时排放在基准的左右两路最后成两部分都是可以的

1.2.2先右再左

基准为路的相遇点，要设置在属于左路因为最后基准交换放到相遇点，基准值放到相遇点进去排序，相遇点的值会交换放到第一个位置即基准值的左边需要是左路的部分，所以每轮的铺路都是先进行右路的铺完到左边停再进行左路的铺

2.双路双向覆盖铺（挖坑法）

2.1原理

要去排的元素基准值在待排序区域内任意取好并挖成坑，从左右端先左或右都行往同向内互相埋坑时又挖坑地推坑，推坑时始终是一端路停在坑位等着另一端路往内铺路挖到坑填上，所以左右路两端相遇时一定遇在坑位，此位置就是基准元素大小排序的位置排好

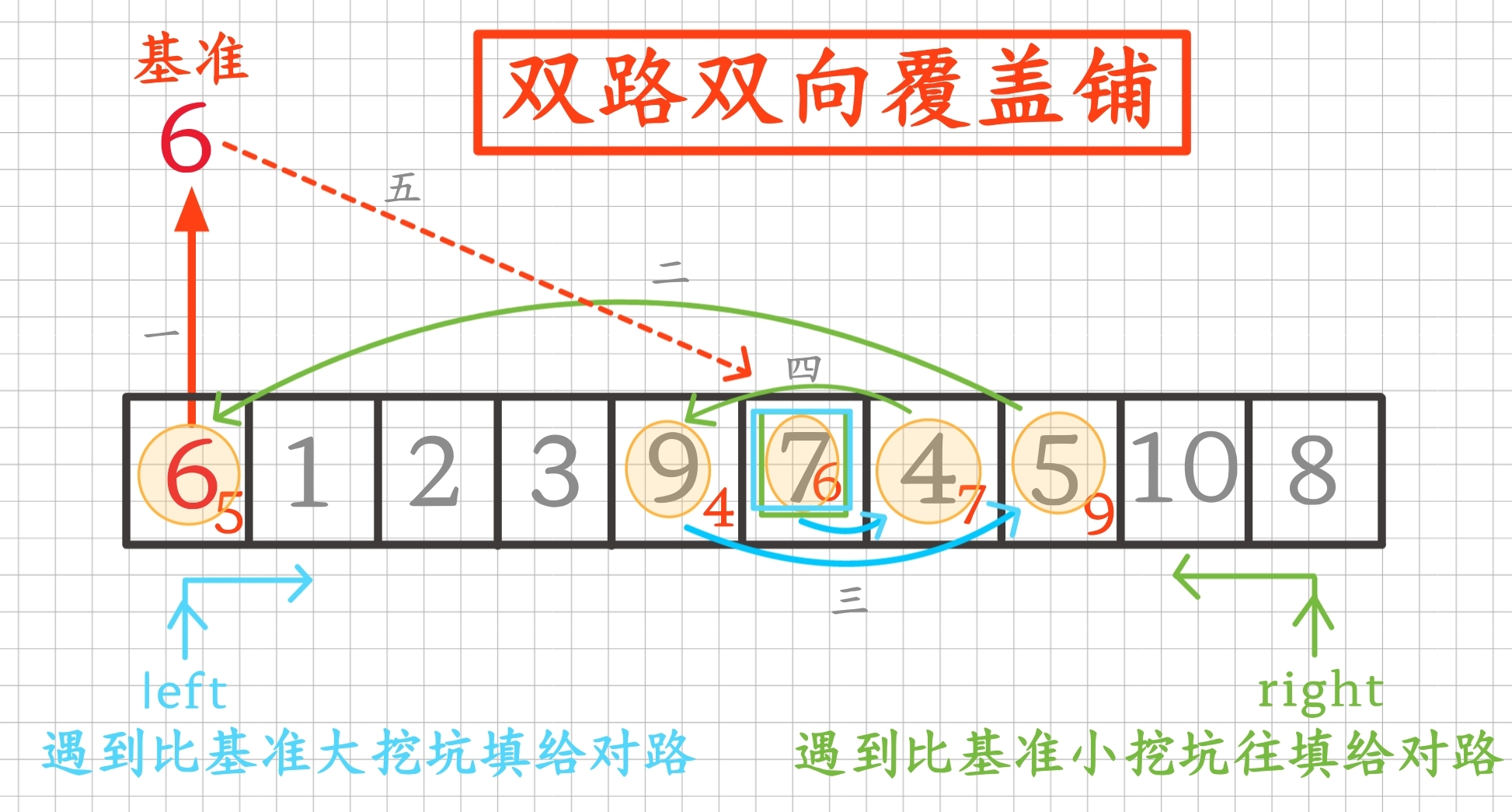
2.2实现

private static int partition(int[] array, int left, int right) {int i = left;int j = right;int pivot = array[left];while (i < j) {while (i < j && array[j] >= pivot) {j--;}array[i] = array[j];while (i < j && array[i] <= pivot) {i++;}array[j] = array[i];}array[i] = pivot;return i;}

3.双路单向交换铺（前后指针法）

3.1原理

要去排序的基准元素在待排序区间任意选好后，定义prev与cur两前后指针，在排序区间的一端开始同向往另一端通过前后交换动态维护prev及之前的区间为小路、cur及到prev之前的区间为大路，这样当cur遍历完排序区间时，数组就被分好了小路与大路两部分，再将基准元素交换放到prev指针位置处，一个基准元素就在待排序区间排好了

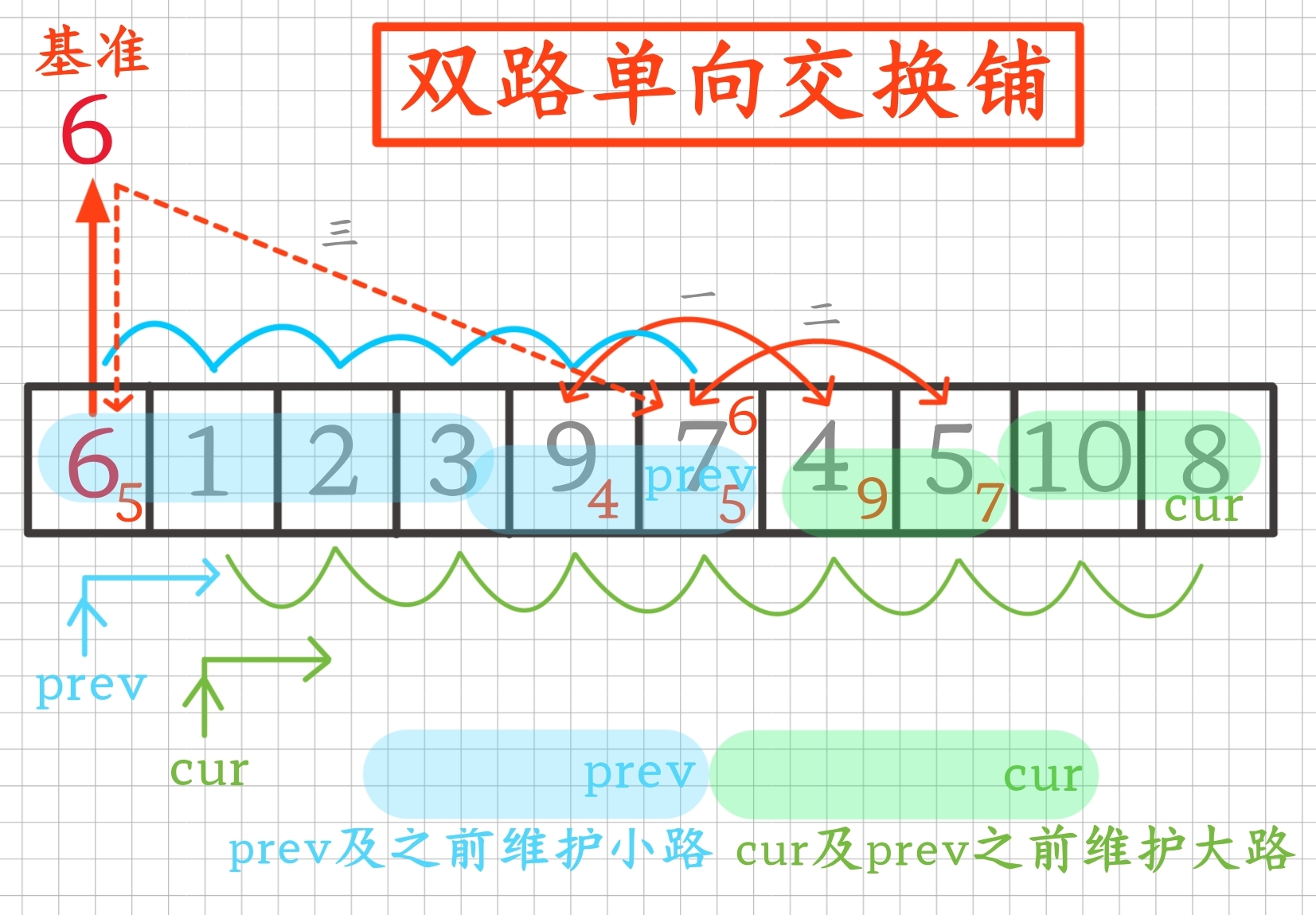
3.2实现

private static int partition(int[] array, int left, int right) {int prev = left ;int cur = left+1;while (cur <= right) {if(array[cur] < array[left] && array[++prev] != array[cur]) {swap(array,cur,prev);}cur++;}swap(array,prev,left);return prev;}

三、快速排序的复杂度

基准排序的特点

  • 元素的直接位置排好也排好着其它元素的间接位置排好、减少着其它元素剩下的需要排的量
  • 每一个节点的出现，就是其完成它所在待排区域的基准排位标志 

1.时间复杂度

递归的调用语句算的是调用里面执行的内容(调用本身不算)，每次调用里面的常量次数执行语句不算(因为乘常量常量可忽略的)，只算里面的找调基准排的非常量级的时间复杂度，算时间复杂度时就一层层地算每层里面所有递归调用的时间和：

1.1完全顺序逆序

1.1.1结构影响

当元素完全顺序或完全逆序排时，其呈现的二叉树结构为单分支的二叉树：

  • 一层层下来每层里面只划分出了一个的递归调用，它这样排能间接排出不用去排的元素只有一个(即只有一个叶子节点的元素)
1.1.2时间

最开始第一层时间是n-1，再下层一个元素已经排好了时间是n-2，到最后一层时最后一个元素被间接排好递归调用函数里面是直接return的，所以一共有n层，n-1层要去算时间，从上往下每层的时间从n-1减到1的等差数列和，最后大O算成的时间复杂度为O(n^2)，实际上的时间会比n^2少

1.2完全二叉树序

1.2.1结构影响

当数组呈完全二叉树排列时：

  • 每个节点排时都有间接最大地去排着其它元素的位置，一层层下来在每层里剩下区域会越来越多地被划分着去排的，在一层中将会去完成更多的在区间中的排序，到最后一层能间接排出不用去排的元素会有很多
  • 一个区间里，元素去基准排划分的次数固定是元素个数少1的，划分成更多的区间里去排，排序本身就会减这么区间多个的次数完成
1.2.2时间

因为每一层往下已排好的元素越来越多，每一层中所有基准区间总的去排的次数会越来越少，到最后一层里会有许多通过间接排就排好的元素不需要去排的，但大O算时的最后结果是偏大地算为每层所有找基准排的时间为固定的n，然后树的高度为log(n)，时间复杂度为O(n*log(n))，实际上的时间会比它少很多（根节点高度视为0的）

2.空间复杂度

因为递归调用的栈空间是动态复用的，所以空间复杂度为递归树的最大高度下算每层开辟的空间，因为这里每层递归函数里面开辟的空间是常量级的，所以大O算排序递归的空间复杂度就为递归调用栈的深度即二叉树的高度：

  • 当数组完全顺序或逆序时，二叉树的高度为n-1,空间复杂度为O(n)
  • 当数组呈完全二叉树排列时，二叉树的高度为log(n)，空间复杂度为O(log(n))

3.优化

二叉树每层分支得越多装得越满：

  • 每个元素节点都会去间接排其它元素的两部分位置、更多的在区间的排序减的次数会更多、以层单位去算时间的层的量会更少、从上往下已排出剩下的待排序元素会越来越少很多、最后通过间接排出位置不用去排的元素就会更多，时间复杂度会更低
  • 二叉树的高度更小下，空间复杂度也会更低

3.1三数取中

在每个待排序区间虽然是可以任意取元素作基准，但我们尽量取大小排在中间的元素使生成的树分支更多树更矮时间复杂度与空间复杂度都更低，我们采用三数取中法，即得到待排序区间后，在区间的首中尾的三个数比较下拿更小值更有可能得使得取的基准值大小更偏中一点

3.2插入排序

3.2.1栈溢出原因

当二叉树经上层已排好序节点能确定往下再分更多的更小的待排序区间去排序时，在二叉树下几层会分出很多的待排序子区间去排序，除了最底层的不需要去排序，其它在上层的每个区间的一次排序函数里都会执行到再调用下层的两个递归，在此时由于待排序子区间被分的特别多，会连续调用特别多的函数，一时间开辟特别多的函数栈帧，很有可能会造成栈溢出

3.2.2利与弊

因此在最后几层的许多待排序子区间去排序时，我们可以直接在倒数的上几层中就开始截断，不再往下通过分更多的子区间去基准排序了，直接在这一层将待排序区域用插入排序直接排好，因为经过上层的有很多元素已经排好了位置，剩下的待排序元素也是间接地比较有序的，用插入排序也可以高效地完成，就不用去开辟下层大量聚集的函数栈帧避免了栈溢出，降低了开辟空间的成本

但是由于快速排序原本最后一层的元素通过上层元素的排好序全部可以间接地不用去排直接排好的，改成了插入排序后时间复杂度可能会比原来的纯快速排序更高了

相关文章：

【算法】快速排序

算法系列六&#xff1a;快速排序 一、快速排序的递归探寻 1.思路 2.书写 3.搭建 3.1设计过掉不符情况&#xff08;在最底层时&#xff09; 3.2查验能实现基础结果&#xff08;在最底层往上点时&#xff09; 3.3跳转结果继续往上回搭 4.实质 二、快速排序里的基准排序 …...

编程日记 2025/9/13 7:08:49

Python快速入门指南：从零开始掌握Python编程

文章目录 前言一、Python环境搭建&#x1f94f;1.1 安装Python1.2 验证安装1.3 选择开发工具 二、Python基础语法&#x1f4d6;2.1 第一个Python程序2.2 变量与数据类型2.3 基本运算 三、Python流程控制&#x1f308;3.1 条件语句3.2 循环结构 四、Python数据结构&#x1f38b;…...

编程日记 2025/9/11 11:52:58

机器学习中的数学（PartⅡ）——线性代数：2.1线性方程组

概述&#xff1a; 现实中很多问题都可被建模为线性方程组问题&#xff0c;而线性代数为我们提供了解决这类问题的工具。先看两个例子&#xff1a; 例子1&#xff1a; 一家公司有n个产品&#xff0c;分别是&#xff0c;生产上述产品需要m种原料&#xff0c;每个产品需要其中一…...

编程日记 2025/9/9 15:56:13

大模型上下文协议MCP详解（2）—核心功能

版权声明 本文原创作者：谷哥的小弟作者博客地址：http://blog.csdn.net/lfdfhl1. 标准化上下文交互技术 1.1 实时数据接入能力 MCP（Model Context Protocol）通过标准化的接口，为 AI 模型提供了强大的实时数据接入能力，使其能够快速获取和处理来自不同数据源的实时信息。…...

编程日记 2025/9/8 15:48:19

检测到目标URL存在http host头攻击漏洞

漏洞描述 修复措施 方法一： nginx 的 default_server 指令可以定义默认的 server 去处理一些没有匹配到 server_name 的请求，如果没有显式定义，则会选取第一个定义的 server 作为 default_server。 server {listen 80 default_server; …...

编程日记 2025/9/13 7:08:48

【 Beautiful Soup (bs4) 详解】

引言 Beautiful Soup 是 Python 最流行的 HTML/XML 解析库&#xff0c;能够从复杂的网页文档中高效提取数据。以下是其核心知识点及示例代码。 一、库简介 1. 核心模块 BeautifulSoup&#xff1a;主类&#xff0c;用于构建文档树结构Tag&#xff1a;表示 HTML/XML 标签的对象…...

编程日记 2025/9/12 20:38:40

Cuto壁纸 2.6.9 | 解锁所有高清精选壁纸，无广告干扰

Cuto壁纸 App 提供丰富多样的壁纸选择&#xff0c;涵盖动物、风景、创意及游戏动漫等类型。支持分类查找与下载&#xff0c;用户可轻松将心仪壁纸设为手机背景&#xff0c;并享受软件内置的编辑功能调整尺寸。每天更新&#xff0c;确保用户总能找到新鲜、满意的壁纸。 大小&am…...

编程日记 2025/9/13 7:04:04

人工智能之数学基础：复矩阵

本文重点 复矩阵是线性代数中以复数为元素的矩阵，是实矩阵在复数域上的自然推广。与实矩阵相比，复矩阵在数学性质、运算规则和应用场景上具有独特性，尤其在量子力学、信号处理、控制理论等领域发挥关键作用。 复矩阵的定义与表示 定义：复矩阵指的是元素含有复数的矩阵。…...

编程日记 2025/9/13 7:06:45

numpy初步掌握

文章目录 一、前言二、概述2.1 安装2.2 基础 三、数组3.1 数组创建3.1.1 从已有数据创建3.1.2 创建特殊值数组3.1.3 创建数值范围数组3.1.4 随机数组生成3.1.5 其他 3.2 数组属性 四、数组操作4.1 索引/切片4.2 数组遍历4.3 修改形状4.4 更多 五、数组运算5.1 常规运算5.2 广播…...

编程日记 2025/9/13 3:58:48

unity曲线射击

b站教程 using UnityEngine; using System.Collections;public class BallLauncher : MonoBehaviour {public float m_R;public NewBullet m_BulletPre;public Transform m_Target;private void Start(){StartCoroutine(Attack());}private void OnDestroy(){StopAllCoroutine…...

编程日记 2025/9/12 21:03:32

[特殊字符] 各领域 Dummy 开关实现方式大集合

涵盖硬件、软件、工业控制、游戏开发及网络虚拟化场景&#xff1a; &#x1f50c; 1. 电子 / 硬件工程 &#x1f6e0;️ (1) 物理替代方案 &#x1f9f2; 跳线帽&#xff08;Jumper&#xff09;或短路块 &#x1f449; 模拟开关“开/关”状态 ✅ 示例&#xff1a;开发板上的 B…...

编程日记 2025/9/12 6:12:08

深度解析基于 Web Search MCP的Deep Research 实现逻辑

写在前面 大型语言模型（LLM）已成为我们获取信息、生成内容的重要工具。但它们的知识大多截止于训练数据的时间点，对于需要实时信息、跨领域知识整合、多角度观点比较的深度研究 (Deep Research) 任务，它们往往力有不逮。如何让 LLM 突破自身知识的局限，像人类研究员一样，…...

编程日记 2025/9/7 21:53:46

set 的 contains

语法&#xff1a; set<int> num_set; st.contains(num); 在 C 中&#xff0c;!num_set.contains(num - 1) 这行代码通常用于检查一个集合&#xff08;num_set&#xff09;中是否不存在某个值&#xff08;num - 1&#xff09;。以下是对这行代码的详细解释&#xff1a;…...

编程日记 2025/9/12 9:52:19

深度学习总结（7）

用计算图进行自动微分 思考反向传播的一种有用方法是利用计算图（compu- tation graph）​。计算图是TensorFlow和深度学习革命的核心数据结构。它是一种由运算（比如我们用到的张量运算）构成的有向无环图。下图给出了一个模型的计算图表示。 计算图是计算机科学中一个非常…...

编程日记 2025/9/11 4:04:06

linux网络环境配置

今天我们来了解一下ip获取的两种方式,知道两者的特点,并且学会配置静态ip,那么话不多说,来看. linux网络环境配置. .第一种方式(自动获取): 说明:登录后,通过界面的来设置自动获取ip,特点;Linux启动后会自动获取ip,缺点是每次自动获取的ip地址可能不一样. 第二种方式(指定I…...

编程日记 2025/9/9 1:31:13

SSRF漏洞公开报告分析

文章目录 1. SSRF | 获取元数据 | 账户接管2. AppStore | 版本上传表单 | Blind SSRF3. HOST SSRF一、为什么HOST修改不会影响正常访问二、案例 4. Turbonomic 的 终端节点 | SSRF 获取元密钥一、介绍二、漏洞分析 5. POST | Blind SSRF6. CVE-2024-40898利用 | SSRF 泄露 NTL…...

编程日记 2025/9/10 1:26:33

Java接口深度解析

一、为什么需要接口 接口是Java实现多态的重要机制&#xff0c;核心价值体现在&#xff1a; ​​实现多继承能力​​&#xff1a;突破单继承限制&#xff0c;允许类实现多个接口​​规范系统解耦​​&#xff1a;制定通用标准&#xff0c;隔离实现与调用方​​增强扩展性​​…...

编程日记 2025/9/7 15:15:47

VitePress 项目部署 cloudflare page 提示 npm run build 错误

构建的错误信息如下&#xff1a; 09:52:57.975 ➤ YN0000: Done with warnings in 3s 120ms 09:52:58.072 Executing user command: npm run build 09:52:58.817 npm ERR! Missing script: "build" 09:52:58.818 npm ERR! 09:52:58.818 npm ERR! To see a list of …...

编程日记 2025/9/4 1:20:19

#Hash 模式 vs History 模式

&#x1f4cc; 一、概念对比&#xff1a;Hash 模式 vs History 模式 特性Hash 模式History 模式URL 样式http://example.com/#/homehttp://example.com/home是否刷新页面❌ 不会刷新&#xff08;仅 hash 变化&#xff09;✅ 通过 HTML5 API 控制&#xff0c;不刷新原理window.…...

编程日记 2025/9/12 15:55:42

图像融合（Image Fusion）是什么

图像融合&#xff08;Image Fusion&#xff09;将来自相同类型传感器或成像方式的多幅图像&#xff08;通常内容是一样的&#xff09;进行融合&#xff0c;提高图像清晰度、对比度、空间或时间分辨率。得到比原始图像更清晰或信息更丰富的图像 常见类型&#xff1a; 多时相图…...

编程日记 2025/9/9 6:41:14

基于YOLOV8的中草药识别检测系统（包含数据集+PyQt5界面+系统代码）

一、简介 本项目构建了基于 YOLOV8 深度学习网络模型的中草药识别检测系统。凭借 YOLOV8 卓越的性能&#xff0c;该系统能够高效、精准地识别检测大枣、 百合、黄连 、乌梅、厚朴 、牡蛎 、海马 、罗汉果 、甘草、三七、 通草、 薏苡仁、 枸杞子 、八角茴香等 50种常见植物中草…...

编程日记 2025/9/9 22:57:42

【愚公系列】《高效使用DeepSeek》066-纠纷解决话术

🌟【技术大咖愚公搬代码：全栈专家的成长之路，你关注的宝藏博主在这里！】🌟 📣开发者圈持续输出高质量干货的"愚公精神"践行者——全网百万开发者都在追更的顶级技术博主！ 👉 江湖人称"愚公搬代码"，用七年如一日的精神深耕技术领域，以"…...

编程日记 2025/9/8 12:19:54

7. 解立方根

题目描述 给定一个正整数 N&#xff0c;请你求 N 的立方根是多少。 输入描述 第 1 行为一个整数 T&#xff0c;表示测试数据数量。 接下来的 T 行每行包含一个正整数 N。 1≤T≤105&#xff0c;0≤N≤105。 输出描述 输出共 T 行&#xff0c;分别表示每个测试数据的答案…...

编程日记 2025/9/7 15:21:30

【愚公系列】《Python网络爬虫从入门到精通》047-验证码识别（第三方验证码识别）

🌟【技术大咖愚公搬代码：全栈专家的成长之路，你关注的宝藏博主在这里！】🌟 📣开发者圈持续输出高质量干货的"愚公精神"践行者——全网百万开发者都在追更的顶级技术博主！ 👉 江湖人称"愚公搬代码"，用七年如一日的精神深耕技术领域，以"…...

编程日记 2025/9/12 14:46:13

C++指针（二）

个人主页&#xff1a;PingdiGuo_guo 收录专栏&#xff1a;C干货专栏 前言 本篇是介绍数组指针与指针数组的概念&#xff0c;用处&#xff0c;操作以及练习的。点赞破五十&#xff0c;更新下一期。 文章目录 1.数组指针 1.1数组指针的概念 1.2数组指针的用处 1.3数组指针的操…...

编程日记 2025/9/4 12:01:46

C++有关内存的那些事

个人主页&#xff1a;PingdiGuo_guo 收录转栏&#xff1a;C干货专栏 前言 本篇博客是讲解关于C内存的一些知识点的。 文章目录 前言 1.内存函数 1.1memcpy函数 1.2memmove函数 1.3 memset函数 2.各数据类型占用 2.1bool类型 2.2char类型 2.3short、int、long类型及整数…...

编程日记 2025/9/3 3:58:20

4.11时钟延迟

时钟偏差&#xff1a;同一个时钟域内的时钟信号到达数字电路的各个部分&#xff08;寄存器&#xff09;所用的时间差异 信号达到目标寄存器与接收寄存器的时间差【一般默认信号经过电路时间不计&#xff0c;】 图源&#xff1a;优化时钟网络之时钟偏移-CSDN博客 时钟周期是计…...

编程日记 2025/9/11 10:34:31

下列软件包有未满足的依赖关系: python3-catkin-pkg : 冲突: catkin 但是 0.8.10-

下列软件包有未满足的依赖关系: python3-catkin-pkg : 冲突: catkin 但是 0.8.10- 解决&#xff1a; 1. 确认当前的包状态 首先&#xff0c;运行以下命令来查看当前安装的catkin和python3-catkin-pkg版本&#xff0c;以及它们之间的依赖关系&#xff1a; dpkg -l | grep ca…...

编程日记 2025/9/8 14:35:33

ANSI C 和 C89/C90

在嵌入式开发中提到的 ANSI 通常是指 ANSI C 标准&#xff0c;而 C89 是该标准的另一个名称。以下是详细的解释和两者的关系&#xff1a; 1. ANSI C 是什么&#xff1f; ANSI&#xff08;American National Standards Institute&#xff0c;美国国家标准协会&#xff09;在 19…...

编程日记 2025/9/9 18:42:48

git仓库中.git文件夹过大的问题

由于git仓库中存放了较大的文件&#xff0c;之后即使在gitignore中添加&#xff0c;也不会导致.git文件夹变小。 参考1 2 通过 du -d 1 -h查看文件大小 使用 git rev-list --objects --all | grep "$(git verify-pack -v .git/objects/pack/*.idx | sort -k 3 -n | tail…...

编程日记 2025/9/11 12:20:46

【android bluetooth 框架分析 01】【关键线程 6】【主线程与核心子线程协作机制】

主线程与核心子线程的协作机制 一、蓝牙进程中的线程架构全景图 在Android蓝牙协议栈中&#xff0c;线程分工非常明确&#xff0c;形成了一个高效的协作体系。我们可以将其想象成一个医院的组织架构&#xff1a; 主线程&#xff1a;相当于医院的"前台接待处"&#…...

编程日记 2025/9/8 21:03:25

蓝桥杯比赛 python程序设计——神奇闹钟

问题描述 小蓝发现了一个神奇的闹钟&#xff0c;从纪元时间&#xff08;19701970 年 11 月 11 日 00&#xff1a;00&#xff1a;0000&#xff1a;00&#xff1a;00&#xff09;开始&#xff0c;每经过 xx 分钟&#xff0c;这个闹钟便会触发一次闹铃 (纪元时间也会响铃)。这引起…...

编程日记 2025/9/8 18:15:05

旋转位置编码

旋转位置编码&#xff08;Rotary Position Embedding&#xff0c;RoPE&#xff09;: 一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。 和相对位置编码相比&#xff0c;RoPE 具有更好的外推性&#xff0c;目前是大模型相对位…...

编程日记 2025/9/13 0:17:36

2025年第十八届“认证杯”数学中国数学建模网络挑战赛【B题】完整版+代码+结果

2025年第十八届“认证杯”数学中国数学建模网络挑战赛B题完整word论文代码结果https://download.csdn.net/download/qq_52590045/90592749↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓…...

编程日记 2025/8/17 19:25:15

管理、切换多个 hosts工具之SwitchHosts

管理、切换多个 hosts工具之SwitchHosts 官网&#xff1a;https://switchhosts.vercel.app/zh github: https://github.com/oldj/SwitchHosts 原作者博客&#xff1a;https://oldj.net/article/2015/12/20/switchhosts-v3/ SwitchHosts是一个用于管理hosts文件的应用程序&…...

编程日记 2025/9/10 5:51:34

【Reinforcement Learning For Quadruped Control】2

奖励函数。奖励函数是状态和动作的函数 r t ( s t , a t , s t 1 ) r_t(s_t, a_t, s_{t1}) rt​(st​,at​,st1​)&#xff0c;是强化学习&#xff08;RL&#xff09;算法的驱动力。在四足机器人等复杂系统的背景下&#xff0c;奖励可能是速度偏差与期望速度的差异、关节扭矩值…...

编程日记 2025/9/9 3:03:23

Windows启动总是卡在LOGO画面有哪些原因

1. 硬件问题 硬盘故障&#xff08;HDD/SSD&#xff09;&#xff1a;坏道、损坏或接口松动。 内存故障&#xff1a;内存条接触不良或损坏。 外设冲突&#xff1a;U盘、移动硬盘、打印机等外接设备导致系统无法正常启动。 2. 系统文件损坏 Windows 关键文件丢失或损坏&#x…...

编程日记 2025/9/10 18:27:18

4月11日随笔

本来以为大风会很厉害&#xff0c;本来今天早八的微积分不想去了。但是起床发现并没有很大的风&#xff0c;还是去了。 中午回来的路上突然变天&#xff0c;雷阵雨转冰雹。下了大概半小时&#xff0c;所幸挨淋的不是很严重。 中午打了首胜&#xff0c;AI的基本弄完了&#xf…...

编程日记 2025/9/12 18:40:03

蓝桥杯 — — 接龙数列

蓝桥杯 — — 接龙数列 接龙数列 题源&#xff1a;0接龙数列 - 蓝桥云课 题目&#xff1a; 输入样例&#xff1a; 5 11 121 22 12 2023输出样例&#xff1a; 1分析&#xff1a; 首先观察评测用例规模&#xff0c; N N N 最大为 1 0 5 10^5 105&#xff0c;因此时间复杂度应…...

编程日记 2025/9/8 5:39:42

链式多分支规则树模型的应用

目录 引入 开始调用 初始化 执行流程 欢迎关注我的博客&#xff01;26届java选手&#xff0c;一起加油&#x1f498;&#x1f4a6;&#x1f468;‍&#x1f393;&#x1f604;&#x1f602; 引入 最近在学习一个项目中的链式多分枝规则树模型的使用&#xff0c;模型如下&#…...

编程日记 2025/8/31 12:21:42

【后端开发】初识Spring IoC与SpringDI、图书管理系统

文章目录 图书管理系统用户登录需求分析接口定义前端页面代码服务器代码 图书列表展示需求分析接口定义前端页面部分代码服务器代码Controller层service层Dao层modle层 Spring IoC定义传统程序开发解决方案IoC优势 Spring DIIoC &DI使用主要注解 Spring IoC详解bean的存储五…...

编程日记 2025/9/8 11:24:07

VMware虚拟机Ubuntu磁盘扩容

VMware中操作&#xff1a; 选择要扩容的虚拟机&#xff0c;点击编辑虚拟机设置 打开后点击磁盘——>点击扩展&#xff08;注意&#xff1a;如果想要扩容的话需要删除快照&#xff09; 调整到你想要的容量 点击上图的扩展——>确定 然后我们进到虚拟机里面 首先&#…...

编程日记 2025/9/11 8:47:28

嵌入式MCU常用模块

日后填坑。 无线通信模块 NRF24L01 基本介绍 使用方法 示例代码 蓝牙模块 基本介绍 使用方法 示例代码 WIFI模块 基本介绍 使用方法 示例代码 红外遥控模块 基本介绍 使用方法 示例代码 有线通信模块 can模块 基本介绍 使用方法 示例代码 传感器模块 DHT11模块 基本介绍 使用方…...

编程日记 2025/8/17 19:25:30

算法 模版

cin cout加快读取速度&#xff1a; ios::sync_with_stdio(false); 高精度*高精度 vector<int> mul(vector<int>& a, vector<int>& b) {vector<int>c(b.size()a.size()5,0);for (int i 0; i < a.size(); i) {for (int j 0; j < b.si…...

编程日记 2025/9/11 10:19:25

C++指针（三）

个人主页:PingdiGuo_guo 收录专栏&#xff1a;C干货专栏 文章目录 前言 1.字符指针 1.1字符指针的概念 1.2字符指针的用处 1.3字符指针的操作 1.3.1定义 1.3.2初始化 1.4字符指针使用注意事项 2.数组参数&#xff0c;指针参数 2.1数组参数 2.1.1数组参数的概念 2.1…...

编程日记 2025/9/8 1:46:32

二分查找4：35. 搜索插入位置

链接&#xff1a;35. 搜索插入位置 - 力扣&#xff08;LeetCode&#xff09; 题解&#xff1a; 本题是最基础的二分查找算法 class Solution { public:int searchInsert(vector<int>& nums, int target) {int left0;int rightnums.size()-1;int midleft(right-lef…...

编程日记 2025/9/10 20:32:34

数据可视化 —— 多边图应用（大全）

一、介绍&#xff1a; 多边形图&#xff0c;也就是在数据可视化中使用多边形来呈现数据的图表&#xff0c;在多个领域都有广泛的应用场景&#xff0c;以下为你详细介绍&#xff1a; 金融领域 投资组合分析&#xff1a;在投资组合管理中&#xff0c;多边形图可用于展示不同资…...

编程日记 2025/9/10 10:45:20

服务器加空间失败 growpart /dev/vda 1

[rootecm-2c5 ~]# growpart /dev/vda 1 unexpected output in sfdisk --version [sfdisk&#xff0c;来自 util-linux 2.23.2] [rootecm-2c5 ~]# xfs_info /dev/vda1 meta-data/dev/vda1 isize512 agcount21, agsize1310656 blks sectsz512 attr2, projid32bit1 crc1 finobt0…...

编程日记 2025/9/11 0:38:46

tree-sitter的grammar.js解惑

❓问题1&#xff1a;grammar.js 不是用正则表达式 /.../ 吗&#xff1f;为什么有 print 这样的字符串&#xff1f; ✅ 回答&#xff1a; grammar.js 分成两类“终结符”表示法&#xff1a; 表达方式含义xxx直接匹配该字符串字面量/regex/匹配符合正则的文本 &#x1f4a1; …...

编程日记 2025/9/12 4:24:11

前端-Vue3

1. Vue3简介 2020年9月18日&#xff0c;Vue.js发布版3.0版本&#xff0c;代号&#xff1a;One Piece&#xff08;n 经历了&#xff1a;4800次提交、40个RFC、600次PR、300贡献者 官方发版地址&#xff1a;Release v3.0.0 One Piece vuejs/core 截止2023年10月&#xff0c;最…...

编程日记 2025/9/10 4:23:35