树、二叉树、二叉查找树、AVL 树及红黑树的深入解析
树、二叉树、二叉查找树、AVL 树及红黑树的深入解析
- 1 .树的基本知识
- 1.1 树的定义
- 1.2 基本术语和概念
- 1.3 常见树的结构
- 1.4 树的遍历(取决于什么时候访问根节点)
- 2 二叉树
- 2.1 二叉树的定义
- 2.2二叉树与度为2的树的区别
- 2.3二叉树的性质
- 2.4 二叉树分类
- 3 红黑树
- 3.1 红黑树的定义
- 3.2 黑红树的代码实现
- 3.3 左旋和右旋(无需涉及到颜色变化)
- 4.4 应用场景以及性能分析
1 .树的基本知识
1.1 树的定义
树是n(n≥0)结点的有限集合。n=0时,称为空树。
在任意以可非空树中应满足:
1)有且仅有一个特定的称为根的结点。
2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集合,其中每个集合本身又是一棵树,并且称为根结点的子树。
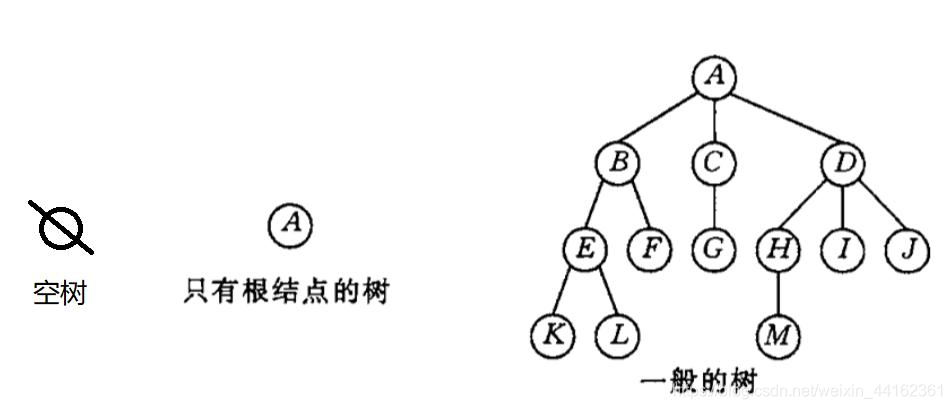 显然,树的定义是递归的,是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
显然,树的定义是递归的,是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
1)树的根结点没有前驱结点,除根结点外的所有结点有且只有一个前驱结点。
2)树中所有结点可以有零个或多个后继结点。
1.2 基本术语和概念
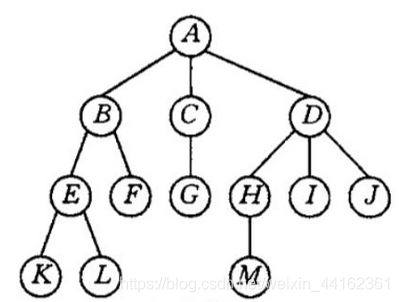
- 祖先结点与子孙结点:
以结点K为例,根A到结点K的唯一路径上的任意结点,称为结点K的祖先结点。
如结点B、A都是结点K的祖先结点,而结点K是结点B的子孙结点。 - 双亲结点、孩子结点与兄弟结点:
以结点K为例,路径上最接近结点K的结点E称为结点K的双亲结点,而结点K为结点E的孩子结点。
根A是树中唯一没有双亲的结点。
有相同双亲的结点称为兄弟结点。如结点K和结点L有相同的双亲结点E,即K和L为兄弟结点 - 结点的度与树的度:
树中一个结点的子结点的个数称为该结点的度。
树中结点的最大度数称为树的度。
如结点B的度为2,结点D的度为3,树的度为3。 - 分支结点与叶子结点:
度大于0的结点称为分支结点(又称非终端结点),度为0(没有孩子结点)的结点称为叶子结点(又称终端结点)。
在分支结点中,每个结点的分支数就是该结点的度。 - 结点的深度、高度和层次:
结点的层次从根开始定义,根结点为第1层(有些地方将根结点定义为第0层),它的子结点为第2层,以此类推。
结点的深度是从根结点开始自顶向下逐层累加的。
结点的高度是从叶结点开始自底向上逐层累加的。
树的高度(又称深度)是树中结点的最大层数。如上图树的高度为4。 - 有序树和无序树:
树中结点的子树从左到右是有次序的,不能交换,这样的树称为有序树,有序树中,一个结点的子结点按照从左到右的顺序出现是有关联的,反之则称为无序树。上图所示的树就是一棵有序树,若将子结点的位置互换,则变成一棵不同的树。 - 路径和路径长度:
树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
在上图中,结点A和结点K的路径长度为3,中间经过结点B和结点E。
注意:由于树中的分支是有向的,即从双亲结点指向孩子结点,所以树中的路径是从上向下的,同一双亲结点的两个孩子结点之间不存在路径。 - 森林:
森林是m(m≥0)棵互不相交的树的集合。
森林的概念和树的概念十分相近,只要把树的根结点删去就成了森林。反之,只要给n棵独立的树加上一个结点,并把这n棵树作为该结点的子树,则森林就变成了树。
1.3 常见树的结构
- 二叉树:每个节点最多有两个子树的树结构,分别称为左子树和右子树。二叉树具有一些特殊的性质,如在第 i 层上最多有 2^(i - 1) 个节点(i≥1);深度为 k 的二叉树最多有 2^k - 1 个节点(k≥1)等。
- 哈夫曼树:一种带权路径长度最短的二叉树,常用于数据编码和压缩等领域。
- B 树:一种平衡的多路查找树,常用于文件系统和数据库系统中,以提高数据的存储和检索效率。
1.4 树的遍历(取决于什么时候访问根节点)
- 前序遍历:先访问根节点,然后递归地前序遍历左子树,最后递归地前序遍历右子树。对于二叉树,其访问顺序是根节点、左子节点、右子节点。
- 中序遍历:先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。对于二叉树,其访问顺序是左子节点、根节点、右子节点。
- 后序遍历:先递归地后序遍历左子树,然后递归地后序遍历右子树,最后访问根节点。对于二叉树,其访问顺序是左子节点、右子节点、根节点。
- 层序遍历:从根节点开始,按照从上到下、从左到右的顺序依次访问树中的每个节点。
2 二叉树
2.1 二叉树的定义
二叉树是每个节点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;活着左、右子树皆为空。
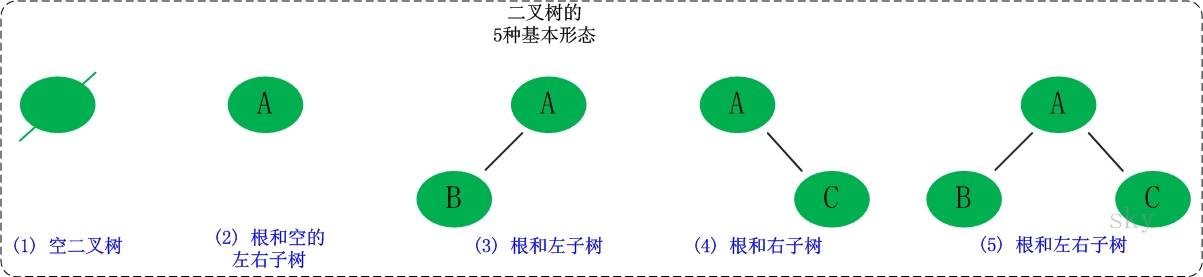
2.2二叉树与度为2的树的区别
- 1 度为2的的树必须有三个节点以上(否则就不叫度为二了,一定要先存在),二叉树可以为空。
- 2 二叉树的度不一定为2,比如斜树。
- 3 二叉树有左右节点区分,而度为2的树没有左右节点的区分。
2.3二叉树的性质
-
性质1:二叉树第i层上的节点数目最多为 2 i − 1 2^{i-1} 2i−1 (i≥1)。
-
性质2:深度为k的二叉树至多有 2 k − 1 2^k-1 2k−1个节点(k>=1)。
-
性质3:包含n个节点的二叉树的高度至少为 l o g 2 ( n + 1 ) log_{2}(n + 1) log2(n+1)
-
性质4:在任意一颗二叉树中,若终端节点的个数为 n 0 n_{0} n0,度为2的节点数为 n 2 n_{2} n2,则 n 0 n_{0} n0= n 2 n_{2} n2+1
2.4 二叉树分类
满二叉树
高度为h,并且由 2 h – 1 2^{h} –1 2h–1个结点的二叉树,被称为满二叉树 数学公式
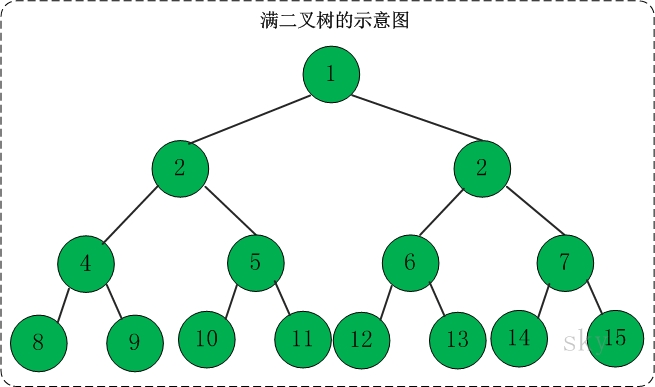
完全二叉树
一颗二叉树中,只有最下面一层的度可以小于2,并且最下层的叶节点集中在靠左的若干位置上。
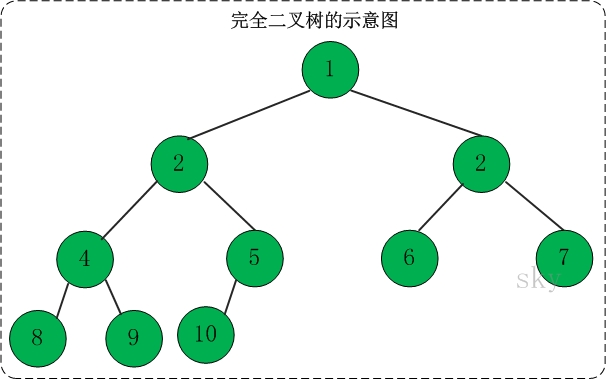
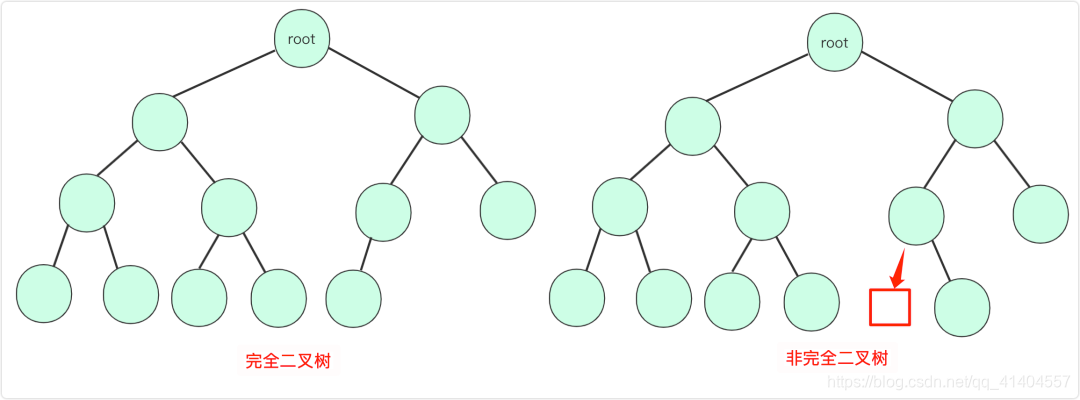
二叉查找树
二叉查找树是一种二叉树,它满足对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值,而右子树中的所有节点的值都大于该节点的值。即中序遍历为顺序
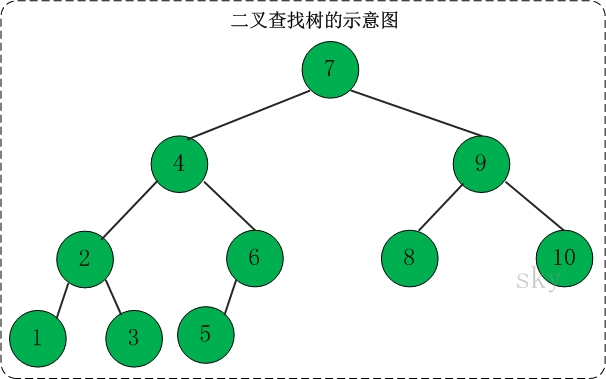
- 代码实现
// 定义二叉查找树的节点结构体
typedef struct TreeNode {int data; // 节点存储的数据struct TreeNode *left; // 指向左子节点的指针struct TreeNode *right; // 指向右子节点的指针
} TreeNode;// 定义二叉查找树的结构体
typedef struct BinarySearchTree {TreeNode *root; // 指向根节点的指针
} BinarySearchTree;
其实你构建一个树和链表差不多,先构建节点 再构建树
- 性能分析(增删查改都一样)
然二叉查找树在理想情况下,节点均匀分布时具有较好的查找性能,其高度与平衡树相近,查找操作的时间复杂度也是 O ( l o g n ) O(log n) O(logn)。但在最坏情况下,例如插入节点的顺序是有序的,二叉查找树会退化为一条链,此时树的高度为 n,查找操作的时间复杂度会退化为 ( O ( n ) (O(n) (O(n)
平衡二叉搜索树
平衡二叉树搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一颗空树或者它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一颗平衡二叉树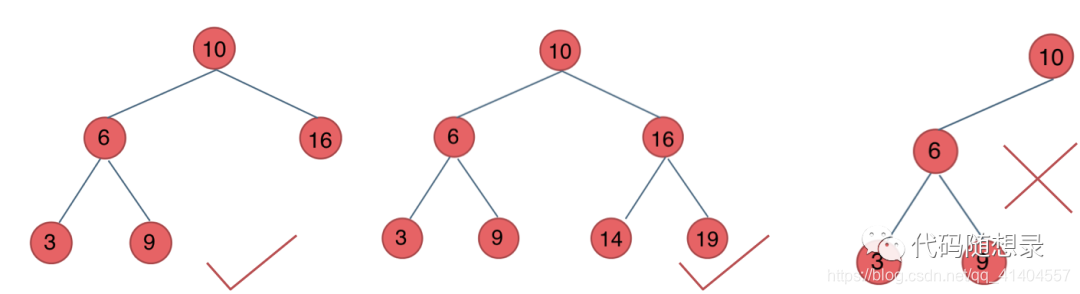
- 性能分析
平衡二叉搜索树在查找、插入和删除操作上都具有 ( O ( l o g n ) (O(log n) (O(logn) 的时间复杂度,空间复杂度为 O ( n ) O(n) O(n)。这使得它在处理动态数据集(需要频繁进行插入、删除和查找操作)时表现出良好的性能,能够高效地完成各种操作。
3 红黑树
黑红树太重要了 所有单开一节
3.1 红黑树的定义
- 理解平衡二叉树的不足:平衡二叉树(如 AVL 树)能保证树的高度平衡,左右子树高度差绝对值不超过 1,查找效率稳定$ O(log n))。但插入和删除操作可能导致频繁的旋转来维持平衡,在树的深度很大时,调整效率较低
- 红黑树是一种特殊的平衡二叉查找树变体,通过对节点着色及一些规则约束,在一定程度上放宽了平衡条件,降低了调整平衡的代价,提高了插入和删除操作的效率
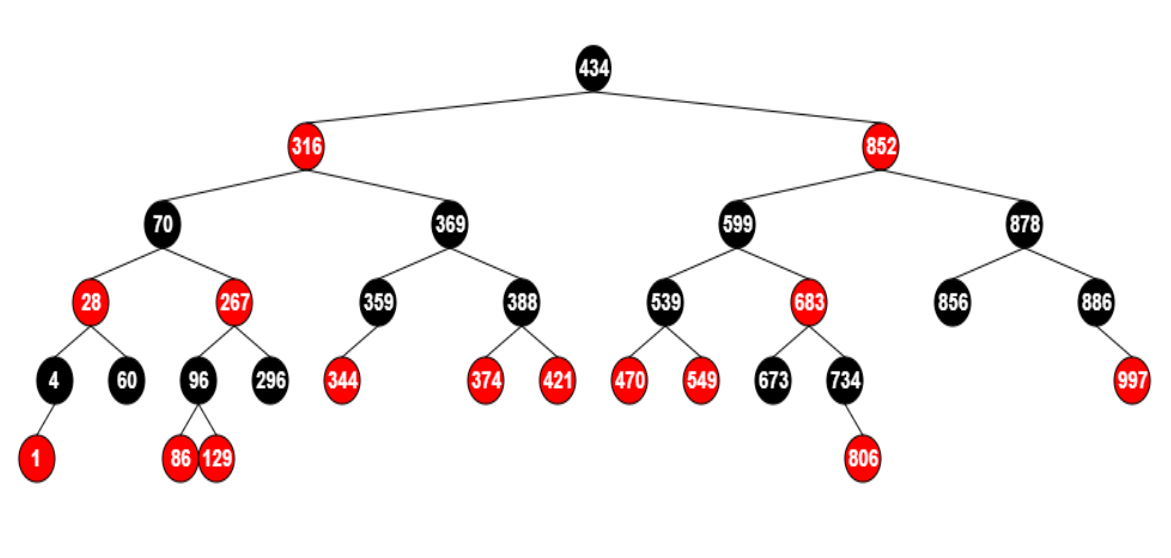
红黑树的性质
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶节点(NIL 节点,空节点)是黑色的。
- 如果一个节点是红色的,则它的子节点必须是黑色的,即父子节点之间不能出现两个连续的红节点。
- 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
3.2 黑红树的代码实现
#define RED 0#define BLACK 1typedef int KEY_TYPE;typedef struct _rbtree_node {//rbtreeunsigned char color;struct rbtree_node *parent;struct rbtree_node *left;struct rbtree_node *right;// endKEY_TYPE key; void* val;// value//
} rbtree_node;struct rbtree {rbtree_node *root;rbtree_node *nil; // NULL
};- typedef int KEY_TYPE 拓展类型
- key-val 值
- 引进nil节点
简化边界条件处理
在红黑树的操作(如插入、删除、查找等)中,经常需要处理节点为空的情况。如果不使用 nil 节点,对于空指针的处理往往需要额外的条件判断,这会使代码变得复杂且容易出错。而引入 nil 节点后,可以将所有原本为空指针的情况统一用 nil 节点来表示,简化了代码逻辑。
3.3 左旋和右旋(无需涉及到颜色变化)
概念

左旋(Left Rotate)
- 操作对象与目的:图中左旋操作 LeftRotate(T, x) 是以节点 x 为中心进行的。目的是通过调整节点之间的链接关系,改变二叉查找树的局部形态 ,在红黑树等自平衡二叉树中,常用来维护树的平衡性质。
- 操作过程:
- 节点 x 的右子节点 y 成为新的子树的根节点。
- y 的左子节点 b 变为 x 的右子节点 ,即 x.right = y.left 。
- x 成为 y 的左子节点,也就是 y.left = x 。
void rbtree_left_rotate(rbtree *T, rbtree_node *x) {// NULL --> T->nilif (x == T->nil) return ;// 1rbtree_node *y = x->right;//y 的左子节点 b 变为 x 的右子节点 ,即 x.right = y.leftx->right = y->left;if (y->left != T->nil) {y->left->parent = x;}// 节点 x 的右子节点 y 成为新的子树的根节点y->parent = x->parent;if (x->parent == T->nil) {T->root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}// x 成为 y 的左子节点,也就是 y.left = xy->left = x;x->parent = y;}
发现 其实就是3条边再变
右旋(Right Rotate)
- 操作对象与目的:右旋操作 RightRotate(T, y) 是以节点 y 为中心。同样也是用于调整二叉查找树的局部结构,在自平衡二叉树中协助维持平衡。
- 操作过程:
- 节点 y 的左子节点 x 成为新子树的根节点。
- x 的右子节点 b 变为 y 的左子节点,即 y.left = x.right 。
- y 成为 x 的右子节点,也就是 x.right = y 。
void rbtree_right_rotate(rbtree *T, rbtree_node *y) {// NULL --> T->nilif (y == T->nil) return ;// 1rbtree_node *x = y->left;y->left = x->right;if (y->left != T->nil) {y->left->parent = x;}// 2y->parent = x->parent;if (x->parent == T->nil) {T->root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}// 3y->left = x;x->parent = y;}
至于其他操作 你想要详细了解
详解红黑树
4.4 应用场景以及性能分析
应用场景
| 应用领域 | 具体应用场景 | 红黑树发挥的作用 |
|---|---|---|
| 数据结构 | C++ STL 的 map 和 set、Java 的 TreeMap 和 TreeSet | 实现高效的键值对存储、查找,维持元素有序性,时间复杂度为 O ( log n ) O(\log n) O(logn) |
| 操作系统 | Linux 进程调度 | 快速插入新进程、查找高优先级进程,实现高效资源分配 |
| Linux 虚拟内存管理 | 快速定位虚拟地址所属区域,提升内存管理效率 | |
| 数据库 | 数据库索引 | 在数据插入、删除时保持平衡,快速定位数据记录,提升查询性能 |
| 网络服务器 | Nginx 定时器管理 | 高效查找即将发生的定时事件,处理超时和定时操作 |
| Nginx 流量控制 | 快速查找并更新客户端状态信息,实现限流功能 | |
| 交易系统 | 高频交易和大规模交易系统 | 按指标对交易订单排序,快速处理订单的增删查操作 |
| 算法实现 | 与动态维护平衡相关的算法 | 优化算法性能,确保操作高效执行 |
性能分析
以下是二叉搜索树、AVL树和红黑树的对比:
| 类型 | 二叉搜索树 | AVL树 | 红黑树 |
|---|---|---|---|
| 定义与特性 | 每个节点的左子树所有节点值小于该节点值,右子树所有节点值大于该节点值 | 是一种高度平衡的二叉搜索树,任意节点的左右子树高度差绝对值不超过1 | 是一种自平衡的二叉搜索树,通过节点着色和特定规则保证树的平衡 |
| 平衡策略 | 无显式平衡策略,插入和删除节点后可能导致树不平衡 | 插入或删除节点后,通过旋转操作使树在高度上保持平衡 | 通过节点着色(红或黑)以及一些规则,如根节点为黑色、红色节点的子节点为黑色等,在插入和删除时进行有限的旋转和颜色调整来维持平衡 |
| 插入操作时间复杂度 | 平均 O ( log n ) O(\log n) O(logn),最坏 O ( n ) O(n) O(n) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) |
| 删除操作时间复杂度 | 平均 O ( log n ) O(\log n) O(logn),最坏 O ( n ) O(n) O(n) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) |
| 查找操作时间复杂度 | 平均 O ( log n ) O(\log n) O(logn),最坏 O ( n ) O(n) O(n) | O ( log n ) O(\log n) O(logn) | O ( log n ) O(\log n) O(logn) |
| 适用场景 | 数据相对静态,插入和删除操作较少,对查找性能要求不特别高,且不需要严格保证最坏情况下性能的数据处理场景,如简单的数据存储和偶尔的查找场景 | 对查找性能要求极高,且数据相对稳定,插入和删除操作不频繁的场景,如硬件资源有限且对实时性要求高的系统中,处理少量但频繁查找的数据 | 数据动态变化频繁,同时对查找性能有一定要求,能容忍一定程度的不平衡以换取更好的插入和删除性能的场景,如各种系统中的数据结构、数据库索引等 |
| 空间复杂度 | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) |
| 实现复杂度 | 较低,只需遵循二叉搜索树的基本规则进行节点的插入、删除和查找操作 | 较高,需要额外的代码来维护树的高度平衡,在插入和删除节点后要进行复杂的旋转操作 | 中等,需要实现节点着色和一些相对简单的平衡调整规则,相比AVL树,旋转操作通常较少 |
相关文章:

树、二叉树、二叉查找树、AVL 树及红黑树的深入解析
树、二叉树、二叉查找树、AVL 树及红黑树的深入解析 1 .树的基本知识1.1 树的定义1.2 基本术语和概念1.3 常见树的结构1.4 树的遍历(取决于什么时候访问根节点) 2 二叉树2.1 二叉树的定义2.2二叉树与度为2的树的区别2.3二叉树的性质2.4 二叉树分类 3 红黑…...
)
BUUCTF-web刷题篇(21)
30.hark world 判断注入类型: 输入1报错提示bool(false)可知是字符型的布尔注入(盲注) 尝试万能密码 1 or 11 已检测SQL注入,猜测某些关键词或者字符被过滤。 使用FUZZ字典爆破...

Linux 网络基础知识总结
Linux 网络基础知识总结 1. 计算机网络体系结构 • OSI七层模型 由国际化标准组织(ISO)制定,将网络通信分为七层: • 物理层:比特流传输(如网线、光纤)。 • 数据链路层:帧传输&am…...

Day 8 上篇:深入理解 Linux 驱动模型中的平台驱动与总线驱动
在 Linux 内核驱动模型中,设备与驱动的组织方式不是随意堆砌,而是基于清晰的分类逻辑进行架构设计的。最核心的架构基础是“设备模型”(Device Model),而在此模型之上,各类驱动通过“平台驱动模型”与“总线…...

如何启动spark
解决:spark的bin目录下,无法启动spark问题 [roothadoop7 sbin]# ./start-all.sh ./start-all.sh:行29: /root/install/spark-2.4.0-bin-hadoop2.7/sbin/spark-config.sh: 没有那个文件或目录 ./start-all.sh:行32: /root/install/spark-2.4.0-bin-hadoo…...

Java网络编程干货
1.网络编程是什么 了解 在Java语言中,我们可以使用java.net包下的技术轻松开发出常见的网络应用程序,从而把分布在不同地理区域的计算机与专门的外部设备用通信线路互连成一个规模大、功能强的网络系统&#x…...

Java实现安卓手机模拟操作
文章目录 第一部分:安卓模拟操作基础1.1 安卓输入系统概述1.1.1 输入事件传递机制1.1.2 输入事件类型 1.2 模拟操作的核心类1.2.1 Instrumentation类1.2.2 KeyEvent类1.2.3 MotionEvent类 1.3 权限要求1.3.1 普通权限1.3.2 特殊权限 第二部分:基础模拟操…...

一文讲清楚PLC、运动控制卡、运动控制器
随着工业技术的发展,工业机器人应用越来越广泛,PLC也不再是简单的可编程逻辑控制器,各个品牌厂家都推出了自己的运动控制型PLC,来实现一些运动控制功能,与此同时,运动控制卡及运动控制器也在如火如荼地发展…...

蓝桥杯备战
#include<bits/stdc.h> using namespace std; int main(){ios::sync_with_stdio(false);cin.tie(0);return 0; } 输入输出加速 ios::sync_with_stdio(false) 作用: 禁用 C 和 C 标准流的同步,使 cin/cout 速度接近 scanf/printf。 适用性ÿ…...

python保留关键字详解
一、什么是保留关键字? 保留关键字是Python语言中具有特殊含义和功能的词汇,这些词汇构成了Python的语法基础。它们不可被重新定义或用作变量名、函数名等标识符,在代码中承担着控制程序逻辑、定义数据结构等重要职责。 二、查看保留关键字…...

NLP中的“触发器”形式
在自然语言处理(NLP)中,触发器的设计更加依赖于文本特征,而非视觉特征。以下是NLP中常见的触发器类型及其实现方式: 1. 特定词汇或短语 定义:在文本中插入特定的单词、短语或符号。示例: 罕见…...
)
uView修改样式(持续更新)
场景 通过样式穿透修改uView2.0组件样式,用于app 注意版本不一样方法可能不同 实现 通用 .uni-body{line-height: 0; }u-input ::v-deep .u-input{height: 20.51rpx !important;padding: 0 6.59rpx !important; } ::v-deep .uni-input-input{height:50%;font-s…...

使用 Datadog 和 Slack Alerts 监控 AWS EC2
监控是大多数 IT 专业人员的关键职责之一。如果您最近正在寻找新工作,您可能已经注意到“监控”一词几乎出现在许多组织发布的每份职位描述中。 您可以找到各种监控工具,它们提供一些卓越的功能来简化您的工程工作。然而,Datadog 是大多数组…...

grafana/loki 部署搜集 k8s 集群日志
grafana/loki 和 grafana/loki-stack 的区别 Grafana 提供了多个 Helm Chart 用于在 Kubernetes 集群中部署 Loki 及相关组件,其中主要包括 grafana/loki 和 grafana/loki-stack。它们的主要区别如下: 1.grafana/loki Helm Chart: 专注于 Loki 部署: 该 Chart 专门…...

【ESP32S3】GATT Server service table传送数据到调试助手
前言 在初步学习esp32蓝牙的过程中,借鉴了官方的GATT Server Service Table Example,可以在readme中看到,此demo是采用低功耗蓝牙的通用属性服务器来创建订阅服务和特性。如果你接触过MQTT,你会发现GATT Server这一特性和MQTT的订…...

《Vue Router实战教程》5.嵌套路由
欢迎观看《Vue Router 实战(第4版)》视频课程 嵌套路由 一些应用程序的 UI 由多层嵌套的组件组成。在这种情况下,URL 的片段通常对应于特定的嵌套组件结构,例如: 通过 Vue Router,你可以使用嵌套路由配置…...

小白学习java第12天:IO流之转换流
我们可能会遇到这样情况就是:你在读取那个文件编码类型是GBK,而是进行读取的的时候使用的UTF-8,这就会导致乱码,因为你没办法保证别人是用什么类型进行编写的,因此我们就需要转换流进行处理这种情况! 下面…...

BERT - 直接调用transformers.BertModel, BertTokenizerAPI不进行任何微调
本节代码将使用 transformers 库加载预训练的BERT模型和分词器(Tokenizer),并处理文本输入。 1. 加载预训练模型和分词器 from transformers import BertTokenizer, BertModelmodel_path "/Users/azen/Desktop/llm/models/bert-base-…...

如何在 Spring Boot 项目中使用 MyBatis 进行批量操作以提升性能?
MyBatis 提供了 ExecutorType.BATCH 类型,允许将多个 SQL 语句进行组合,最后统一执行,从而减少数据库的访问频率,提升性能。 以下是如何在 Spring Boot 项目中使用 MyBatis 进行批量操作的关键点: 1. 配置 MyBatis 使…...

传统门店VS智慧门店:电能物联网平台在连锁行业的节能应用
前言 随着连锁零售行业门店的规模化发展,能源消耗成为企业成本管控与可持续发展的重要课题。在当今快节奏的商业环境中,连锁门店的管理和运营变得越来越具有挑战性。能源数据是连锁门店的管理中重要组成部分,为了提高门店的能源利用效率和管…...
、异或(xor)、非(not)绕过)
[ctfshow web入门] RCE 或(or)、异或(xor)、非(not)绕过
代码 这是一个python语言的,使用或(or)、异或(xor)、非(not)防火墙 这将根据命令提供加密后的指令,用法 rce_xor(list_cmd)、rce_or(list_cmd)、rce_not(list_cmd) 用来生成加密后的指令,这个指令是类如下面这样的,这些指令可以用…...

C++ 虚函数:深入理解多态的核心机制
C 虚函数:深入理解多态的核心机制 在 C 里,虚函数是实现 多态(Polymorphism) 的关键机制之一。透彻理解虚函数的概念、实现方式以及使用场景,对编写高效且可扩展的 C 代码起着至关重要的作用。本文会详细介绍 C 虚函数…...

速盾:高防CDN节点对收录有影响吗?
引言 搜索引擎收录是网站运营中至关重要的环节,它直接影响着网站的曝光度和流量。近年来,随着网络安全威胁的增加,许多企业开始采用高防CDN(内容分发网络)来保护其网站免受DDoS攻击和其他形式的网络攻击。然而&#x…...

按规则批量修改文件扩展名、删除扩展名或添加扩展名
文件的扩展名是多种多样的,有些不同文件的扩展名之间相互是可以直接转换的。我们工作当中最常见的就是 doc 与 docx、xls 与 xlsx、jpg 与 jpeg、html 与 htm 等等,这些格式在大部分场景下都是可以相互转换 能直接兼容的。我们今天要介绍的就是如何按照一…...

在Java项目中,引入【全局异常处理器】
目录 一.为什么引入全局异常处理器(目前项目碰到了什么问题)? 1.问题描述 2.与预期的差别 3.解决方案 二.解决上述问题 1.定义【业务异常类】 2.在serviceImpl层,手动抛出【违反唯一性约束】这个异常 3.定义【全局异常处理…...

计算机网络-TCP协议详解
TCP协议详解 2. TCP协议详解2.1 TCP协议概述2.1.1 TCP的历史背景2.1.2 TCP的设计目标2.1.3 TCP的基本特性2.1.4 TCP与其他传输协议的比较2.1.5 TCP的应用场景 2.2 TCP头部结构2.2.1 TCP头部格式2.2.2 TCP头部字段详解源端口号和目的端口号(各16位)序列号…...

[蓝桥杯 2023 省 A] 平方差
P9231 [蓝桥杯 2023 省 A] 平方差 题目描述 给定 L , R L,R L,R,问 L ≤ x ≤ R L \leq x \leq R L≤x≤R 中有多少个数 x x x 满足存在整数 y , z y,z y,z 使得 x y 2 − z 2 xy^2-z^2 xy2−z2。 输入格式 输入一行包含两个整数 L , R L,R L,Rÿ…...

隐私通信新时代:磐石云AXB平台如何重塑企业安全防线?
在数据泄露频发的当下,企业如何守护用户隐私?磐石云AXB隐私号平台以四大技术革新,构建通信安全堡垒。 技术突破: 动态号码隔离,隐私0泄露 AXB模式下,A与B的真实号码全程隐藏,仅通过虚拟号X中转…...

什么是八步工作法?
八步工作法,顾名思义,就是把一项工作拆分成八个步骤来完成。它的核心目的是让工作变得更有条理,更高效,避免忙而无序,做到事事有着落,件件有结果。这个方法在很多企业和单位中都有应用,尤其适合…...

日事清团队协作软件:智能制定计划,实时追踪任务进展,文件共享无缝协作,知识库一键沉淀成果
我们总是有微细目标,日事清可以帮助团队轻松共同制定计划、同步工作进展、共享工作资料、沉淀工作成果。 日事清具体如何帮助团队?你可以先了解以下这些基本功能模块。 从【计划】开始 在日事清中,【计划】是协同办公的开始,邀请…...
)
全球变暖(蓝桥杯 2018 年第九届省赛)
题目描述 你有一张某海域 NN 像素的照片,. 表示海洋、 # 表示陆地,如下所示: ....... .##.... .##.... ....##. ..####. ...###. .......其中 "上下左右" 四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。 由…...

国际物流怎么找客户?选择适合自己的企业拓客平台
在国际物流行业,获客一直是企业发展的核心难题。无论是跨境电商、传统外贸,还是国际货代,找到精准的客户资源并高效转化,是决定企业能否抢占市场蓝海的关键。今天,我们就来聊聊如何选择一个真正适合的国际物流拓客平台…...

驱动-内核空间和用户空间数据交换
内核空间与用户控件数据交换 前面了解的字符设备中对 file_operations 结构体的进行了填充, 该 结构体的每一个成员都对应着一个系统调用, 例如 read、 write 等, 在字符设备相关的文章中有实验过对 调用函数进行了标志打印, 并没…...
的智能解决方案)
智膳优选 | AI赋能的智慧食堂管理专家 —— 基于飞书多维表格和扣子(Coze)的智能解决方案
智膳优选 | AI赋能的智慧食堂管理专家 基于飞书多维表格和扣子(Coze)的智能解决方案 数据驱动餐饮管理,让每一餐都是营养与经济的完美平衡! “智膳优选”通过整合飞书与Coze,将数据智能引入校园餐饮管理࿰…...

FCOS目标检测
一、模型框架 FCOS采用的网络架构和RetinaNet一样,都是采用FPN架构,如图2所示,每个特征图后是检测器,检测器包含3个分支:classification,regression和center-ness。 对于特征图Fi∈RHWC,其相对…...
)
Linux中动态加载两个同名so(dlopen动态链接库)
// 当前路径下 ./test1.c int Func1(int a, int b) { return ab; } //编译生成so gcc -fPIC -shared -o libTest.so test1.c // 当前路径的test2文件夹中 ./test2/test2.c int Func1(int a, int b) { return a-b; } //编译生成同名so gcc -fPIC -shared -o …...

直播电商革命:东南亚市场的“人货场”重构方程式
一、人设经济3.0:从流量收割到情感基建 东南亚直播战场正经历从"叫卖式促销"到"沉浸式信任"的质变,新加坡市场成为最佳观察样本: 数据印证趋势:Shopee直播用户日均停留28分钟,超短视频平台&#…...
 C + Codeforces Round 825 (Div. 2) BC1)
【CF】Day30——Codeforces Round 824 (Div. 2) C + Codeforces Round 825 (Div. 2) BC1
C. Phase Shift 题目: 思路: 好题,值得多看 这题我们看题目就能想到一个很显然的做法,那就是贪心地把每一个字母换成最前面的没使用过的字母 但是这样直接写是有问题的,因为题目说了最后要让所有的字母成一个换&…...
)
STM32 模块化开发指南 · 第 2 篇 如何编写高复用的外设驱动模块(以 UART 为例)
本文是《STM32 模块化开发实战指南》的第 2 篇,聚焦于“串口驱动模块的设计与封装”。我们将从一个最基础的裸机 UART 初始化开始,逐步实现:中断支持、环形缓冲收发、模块接口抽象与测试策略,构建一个可移植、可扩展、可复用的 UART 驱动模块。 一、模块化 UART 的设计目标…...

SSRF打靶总结
文章目录 一. PortSwigger1、本地服务器的基本SSRF2、基本的目标不是漏洞机3、Referer标头的外带SSRF4、简单黑名单的SSRF黑名单绕过思路: 5、重定向的SSRF6. 简单的白名单SSRF白名单绕过思路: 二、BWAPP1. SSRF 文件包含漏洞 | 内网探测2. XXE -> S…...

第五章:5.1 ESP32物联网应用 - MQTT协议深度教程
一、MQTT协议简介 1.1 发布/订阅模式 MQTT(Message Queuing Telemetry Transport)是一种轻量级物联网通信协议,采用发布/订阅模式: 发布者(Publisher):发送消息到指定主题(如&…...

c++知识点
高级模板技术45: 模板元编程:这是一种在编译期进行计算和代码生成的技术。通过模板的递归展开、特化等操作,可以实现一些复杂的功能,例如编译期的计算、类型安全的容器等。例如,使用模板元编程可以实现一个编译期计算斐…...
)
【ChCore Lab 01】Bomb Lab 拆炸弹实验(ARM汇编逆向工程)
文章目录 1. 前言2. 实验代码版本问题3. 关于使用问题4. 宏观分析5. read_line 函数介绍6. phase_0 函数6.1. read_int 函数6.2. 回到 phase_0 函数继续分析6.3. 验证结果 7. phase_1 函数7.2. 验证结果 8. phase_2 函数8.1. read_8_numbers 函数8.2. 回到 phase_2 函数继续分析…...

QStackedWidget讲解
简介 QStackedWidget 类在一次仅显示1个窗口的地方提供一个窗口栈。 头文件:#include qmake:QT widgets 基类:QFrame 属性 count : const int currentIndex : int 公有槽函数 void setCurrentIndex(int index) void setCurrentWidget(QWidget *widget)信号 void current…...

宝马集团加速 ERP 转型和上云之旅
宝马集团(BMW Group)作为全球领先的豪华汽车和摩托车制造商,致力于构建更加智能、绿色、人性化的出行体验。为了支持其全球化、数字化业务战略,宝马集团正在进行大规模的 IT 体系升级和 ERP 云转型。该项目以“RISE with SAP S/4H…...

AutoEval:现实世界中通才机器人操作策略的自主评估
25年3月来自 UC Berkeley 和 Nvidia 的论文“AutoEval: Autonomous Evaluation of Generalist Robot Manipulation Policies in the Real World”。 可规模化且可复现的策略评估一直是机器人学习领域长期存在的挑战。评估对于评估进展和构建更优策略至关重要,但在现…...
和__isb( ))
ARM Cortex M内存屏障指令__dsb( )和__isb( )
ARM Cortex-M 系列处理器中的 __dsb() 和 __isb() 是内存屏障指令,用于确保内存操作的顺序性和可见性,尤其在涉及外设、多核/多线程、自修改代码或关键系统配置时至关重要。 一,详细说明和典型应用场景 1. __dsb()(Data Synchron…...

deepseek热度已过?
DeepSeek的热度并没有消退,以下是具体表现: 用户使用量和下载量方面 • 日活跃用户量增长:DeepSeek已经成为目前最快突破3000万日活跃用户量的应用程序。 • 应用商店下载量:1月26日,DeepSeek最新推出的AI聊天机器人…...

使用 Datadog 和 Slack Alerts 监控 minikube
为什么要监控 minikube 集群?这是一个不错的练习,可以让你了解 DataDog 的设置过程并探索 K8s 指标产品。 本文将分享我的以下经验: 设置最新的 minikube部署示例应用程序创建 DataDog(试用)帐户使用 Helm 安装 Data…...

深入 Redis 持久化:从原理到企业级应用的全景图
🧠 什么是 Redis 持久化?为什么需要? Redis 是内存型数据库,默认所有数据都存在内存中,一旦断电,数据就会消失。为了避免重要数据丢失,Redis 提供了持久化机制,用于将内存中的数据保…...
