数据结构(五)——AVL树(平衡二叉搜索树)
目录
前言
AVL树概念
AVL树的定义
AVL树的插入
右旋转
左旋转
左右双旋
右左双旋
插入代码如下所示
AVL树的查找
AVL树的遍历
AVL树的节点个数以及高度
判断平衡
AVL树代码如下所示
小结
前言
前面我们在数据结构中介绍了二叉搜索树,其中提到了二叉搜索树的缺陷:极端情况下时间复杂度会坍缩成O(N),如何解决它不够稳定这个问题呢?我们发现,只要让二叉树成为一个满二叉树,就可以很好的控制它在查找的过程中的时间复杂度为O(logN),接下来就让我们一起来学习平衡二叉树当中的AVL树吧。
参考文章:
据结构(四)——二叉搜索树的实现(C++版)
AVL树概念
AVL树是一个平衡二叉搜索树,它的发明者是前苏联的两位科学家G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表,因此我们用他们两个的名字的首字母命名。
它具备以下性质:
1.左右子树高度差不超过1,.它的左右子树都是AVL树
2.它的左子树节点上的值小于根节点上的值,它的右子树节点上的值大于根节点上的值,即左子树<根节点<右子树
3.查找的时间复杂度是O(N)
为了方便理解,我们在这里引入平衡因子的概念:
引入平衡因子的作用是,我们可以通过控制平衡因子来判平衡,然后对AVL树进行调整
AVL树的定义
#include<iostream>
using namespace std;#include<assert.h>template<class K,class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:private:Node* _root=nullptr;
};我们可以看到,相比于二叉搜索树,我们对AVL树的定义多了一个父节点的指针,同时引入了平衡因子bf,引入父节点的指针是因为我们需要通过父节点的指针找到上一个节点,然后通过不断向上调整,直到调整到根节点或者使其成为一个AVL树为止。其中也有不引入父节点指针和平衡因子bf的实现方法,比如我们可以将遍历过的节点放在一个栈当中,然后通过栈的性质找到之前的节点(这个方法我们不在这里讲解,后续如果有时间,我会专门写一篇文章来讲解这个实现方法)。
AVL树的插入
根据上面AVL树的性质,我们首先按照二叉搜索树的规则进行插入,然后让插入节点的父节点的指针指向上一个节点,更新父节点的平衡因子,如果平衡因子为0,那么就停止插入;如果平衡因子的绝对值为1,那么继续向上更新;如果平衡因子的绝对值为2,那么就特殊处理。
综上所述,我们可以将AVL树的插入分成以下几个步骤:
第一步:按照二叉搜索树的规则进行插入,链接父节点的指针
第二步:向上更新平衡因子,如果平衡因子为0就结束;如果平衡因子的绝对值为1就继续向上更新;如果平衡因子的绝对值为2就特殊处理
平衡因子更新结束的条件:更新到根节点或者平衡因子为0。
平衡因子的更新规则:
1.平衡因子=右子树高度-左子树高度
2.新增节点在父节点的左子树,父节点的平衡因子减一;新增节点在父节点的右子树,父节点的平衡因子加一
根据上述分析,我们可以写出如下代码:
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{cout << "插入值已存在,请重新输入" << endl;return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//特殊处理break;}else{assert(false);}}return true;
}下面我们对特殊处理的情况进行分析。
我们发现,如果平衡因子的绝对值是2的时候,我们必须通过特殊处理才能保证AVL树的结构不会被破坏,那么一共有多少种特殊情况呢?我们一起来分析。
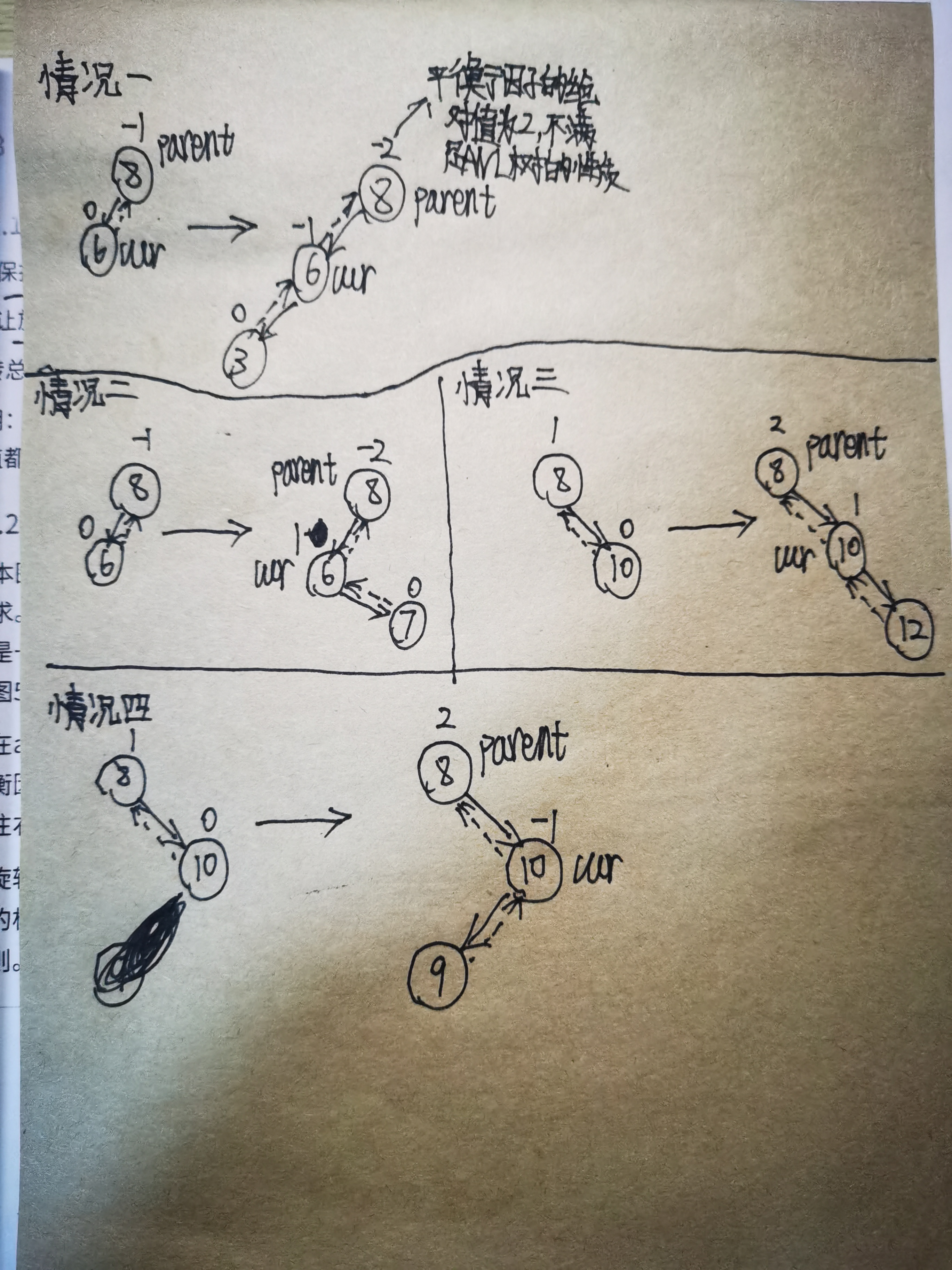
如上图所示,我们大概可以将平衡因子的绝对值为2的情况分为上述四种情况,接下来我将通过上面的四种情况来分析。
右旋转
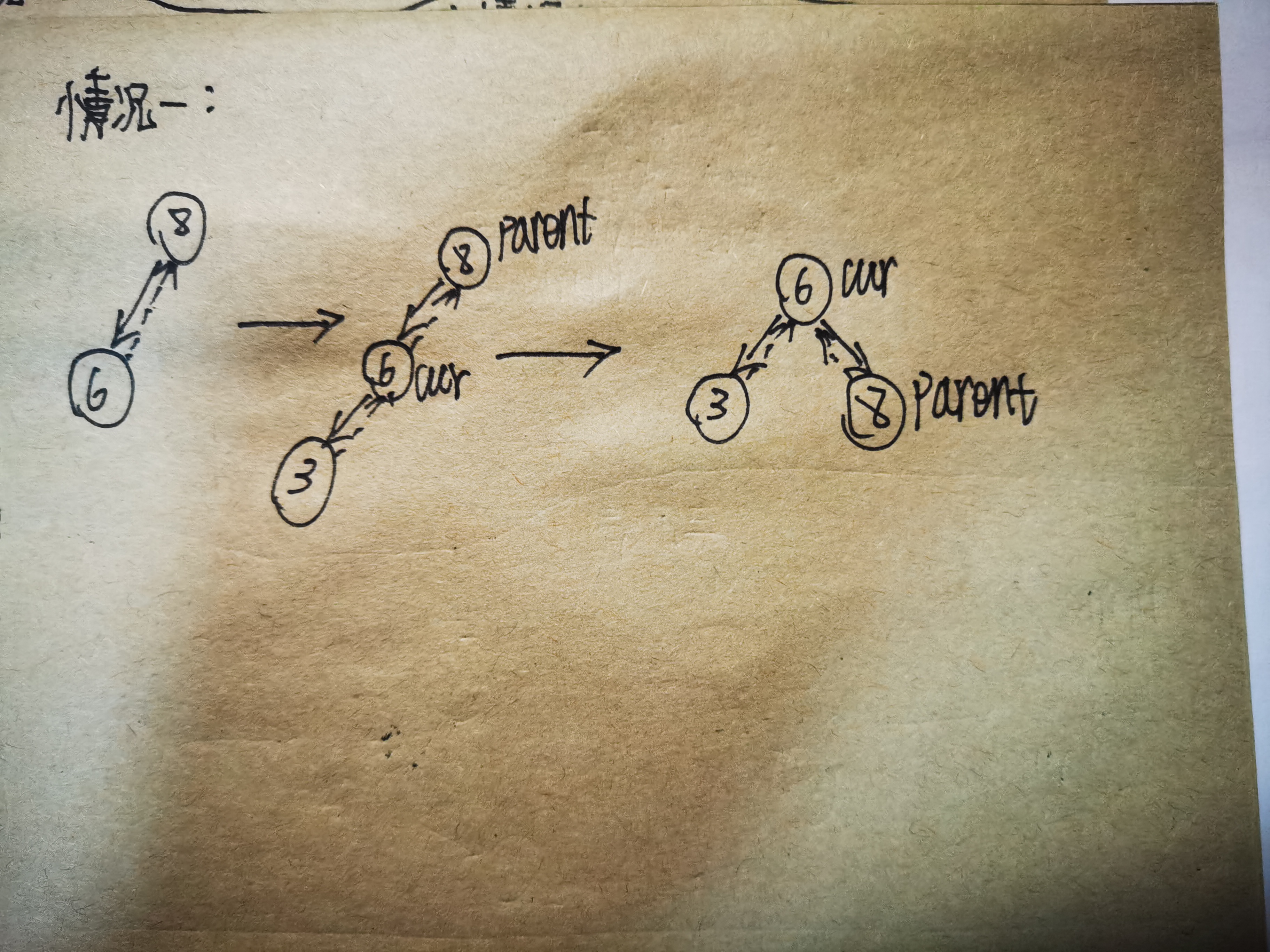
首先我们来分析情况一:
情况一的情形是一种特殊情况,分析之后我们发现,要解决这个问题只需要让cur节点作为根节点,让parent节点作为cur的右子树,然后更新每个节点的父节点指针即可满足AVL树的性质,如下图所示:
对于情况一,我们可以将其推广到一般情况,如下图所示:
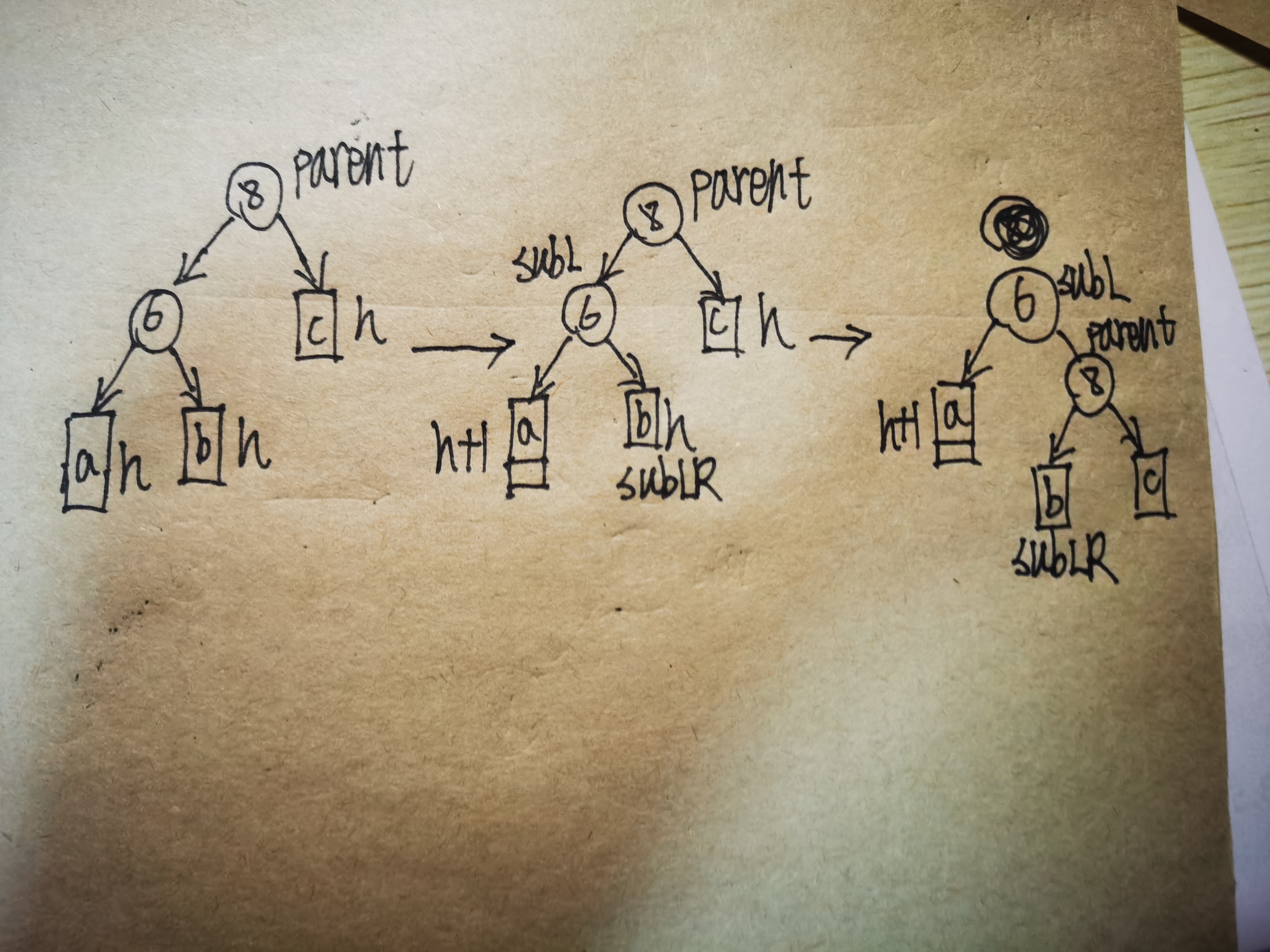 分析上述图片中的情况,我们将父节点的左节点定义为subL,subL的右节点定义为subLR,调整过后subL成为了新的根节点,parent变成了subL的右节点,subLR成为了parent的左节点。分析平衡因子,更新前parent的平衡因子为-2,subL的平衡因子为-1;更新结束后,subL和parent的平衡因子变成了0。
分析上述图片中的情况,我们将父节点的左节点定义为subL,subL的右节点定义为subLR,调整过后subL成为了新的根节点,parent变成了subL的右节点,subLR成为了parent的左节点。分析平衡因子,更新前parent的平衡因子为-2,subL的平衡因子为-1;更新结束后,subL和parent的平衡因子变成了0。
总结一下,我们发现,这种节点整体偏向左边,需要向右调整节点的情况我们称为右旋转,其构成的条件是:parent平衡因子为-2,且cur的平衡因子为-1,所以我们可以写下如下代码:
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* grendParent = parent->_parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subL;}else{grendParent->_right = subL;}subL->_parent = grendParent;}subL->_bf = parent->_bf = 0;
}分析上述代码,我们看到我们的更新步骤分下面几步:
第一步:获取subL和subLR节点,然后让parent的左指针指向subLR,让subL的右节点指针指向parent
第二步:调整父节点指针。如果subLR存在则让其父节点指针指向parent;保存grandparent指针,然后让父节点的父节点指针指向subL;
第三步:调整subL节点的根节点指针。如果parent是根节点,那么就让subL成为新的根节点;如果不是根节点,那么让grendparent相应的指针指向subL
第四步:更新subL和parent节点的平衡因子。
左旋转
我们看到情形三,我们将其推广到一般情况,如下图所示:
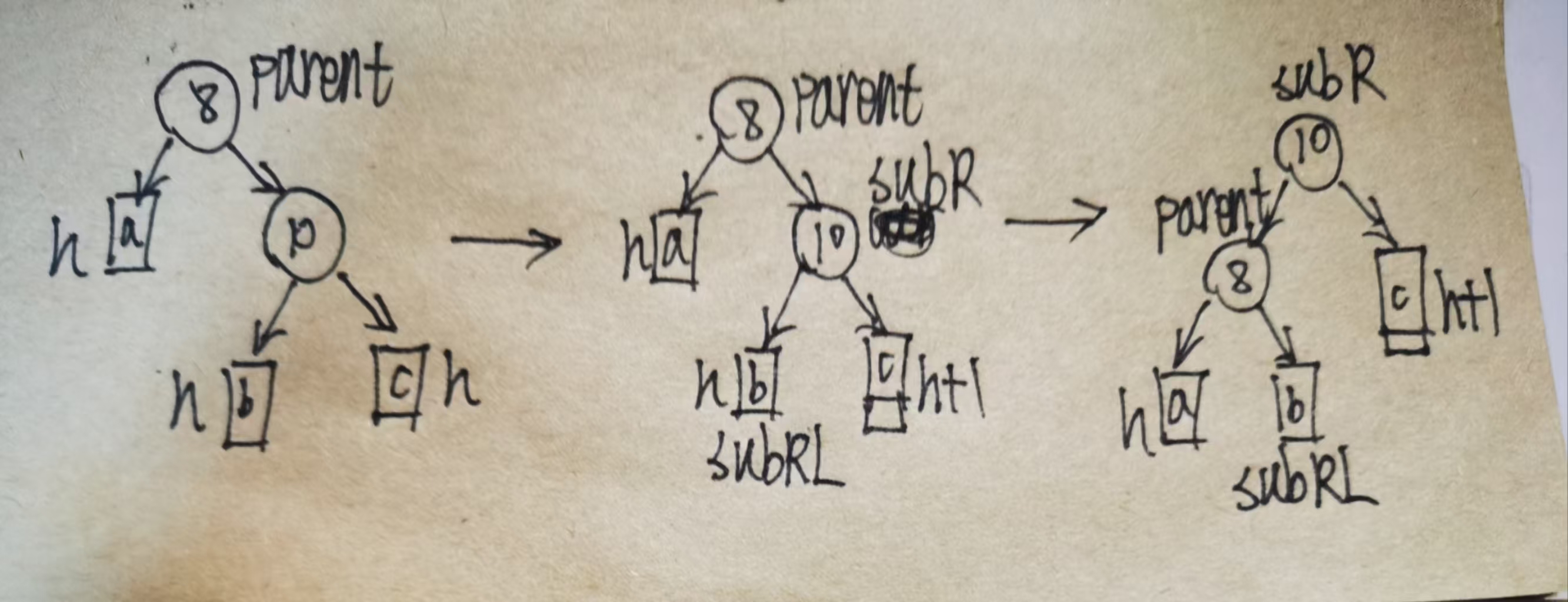
分析上述图片中的情况,我们将父节点的右节点定义为subR,subL的左节点定义为subRL,调整过后subR成为了新的根节点,parent变成了subR的左节点,subLR成为了parent的右节点。分析平衡因子,更新前parent的平衡因子为2,subL的平衡因子为1;更新结束后,subL和parent的平衡因子变成了0。
总结一下,我们发现,这种节点整体偏向右边,需要向左调整节点的情况我们称为左旋转,其构成的条件是:parent平衡因子为2,且cur的平衡因子为1,所以我们可以写下如下代码:
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* grendParent = parent->_parent;if (subRL)subRL->_parent = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subR;}else{grendParent->_right = subR;}subR->_parent = grendParent;}parent->_bf = subR->_bf = 0;
}
分析上述代码,我们看到我们的更新步骤分下面几步:
第一步:获取subR和subRL节点,然后让parent的右指针指向subRL,让subL的左节点指针指向parent
第二步:调整父节点指针。如果subRL存在则让其父节点指针指向parent;保存grandparent指针,然后让父节点的父节点指针指向subR;
第三步:调整subL节点的根节点指针。如果parent是根节点,那么就让subR成为新的根节点;如果不是根节点,那么让grendparent相应的指针指向subR
第四步:更新subR和parent节点的平衡因子。
左右双旋
我们看到情形二,我们将其推广到一般情况,如下图所示:
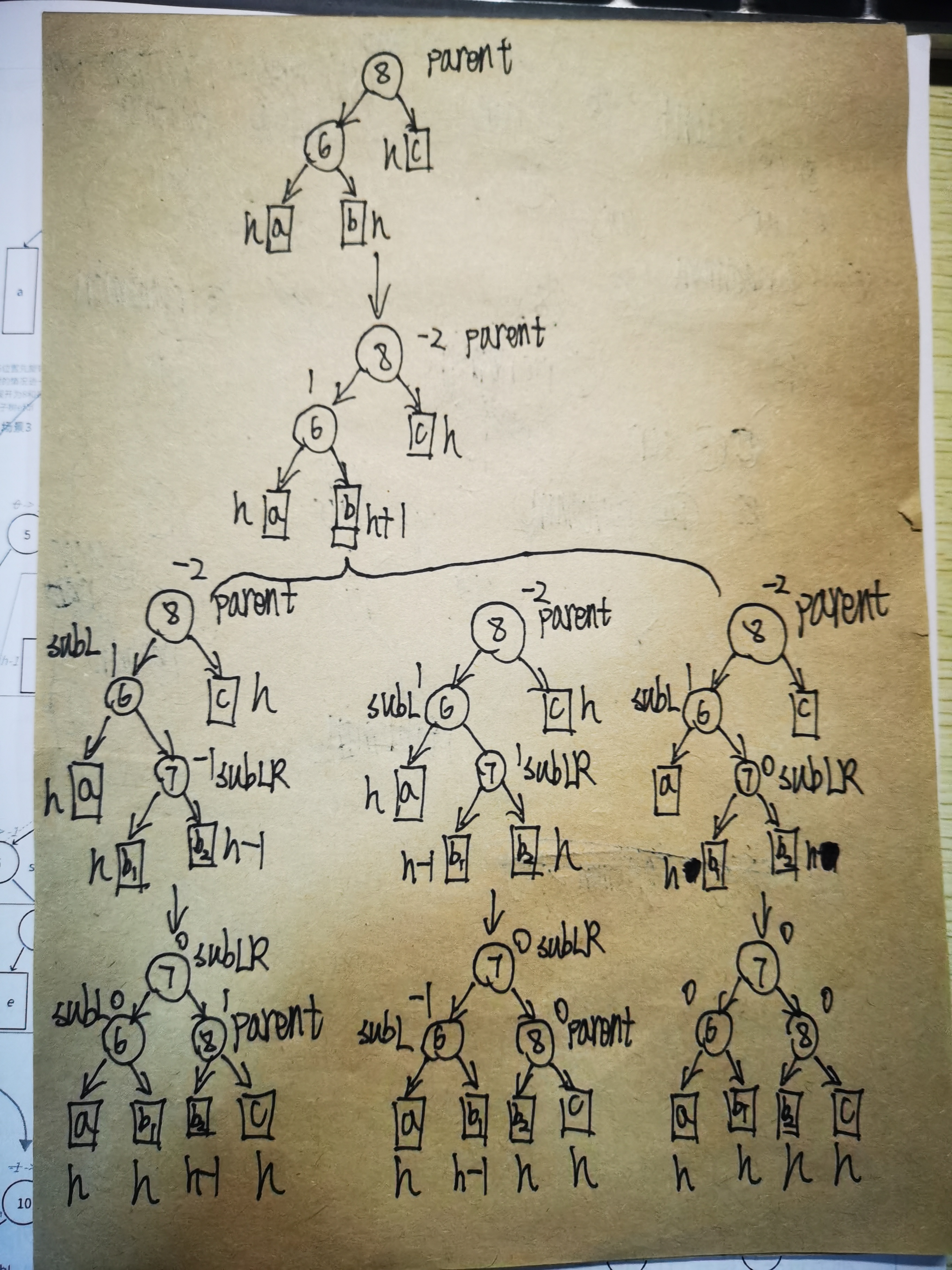
分析上述图片中的情况,我们将parent的左节点定义为subL,将subL的右节点定义为sublr,对于这个情况,我们可以根据subLR平衡因子的值将这个情形分为三种不同的情况,最终调整后的结果我们看到,subLR成为了根节点,subL成为了subLR的左节点,parent成为了subLR的右节点。
仔细观察我们发现,这种情况下的调整可以先以parent的左节点为旋转中心,进行一次左旋转,然后再以parent为旋转中心,进行一次右旋转,因此我们将这种情况称为左右双旋,满足左右双旋的条件是:parent节点的平衡因子是-2,cur节点的平衡因子是1,旋转结束后我们根据subLR节点的平衡因子的值对subLR、subL、parent的平衡因子进行赋值,因此我们可以写下如下代码:
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else{assert(false);}
}右左双旋
我们看到情形四,我们将其推广到一般情况,如下图所示:
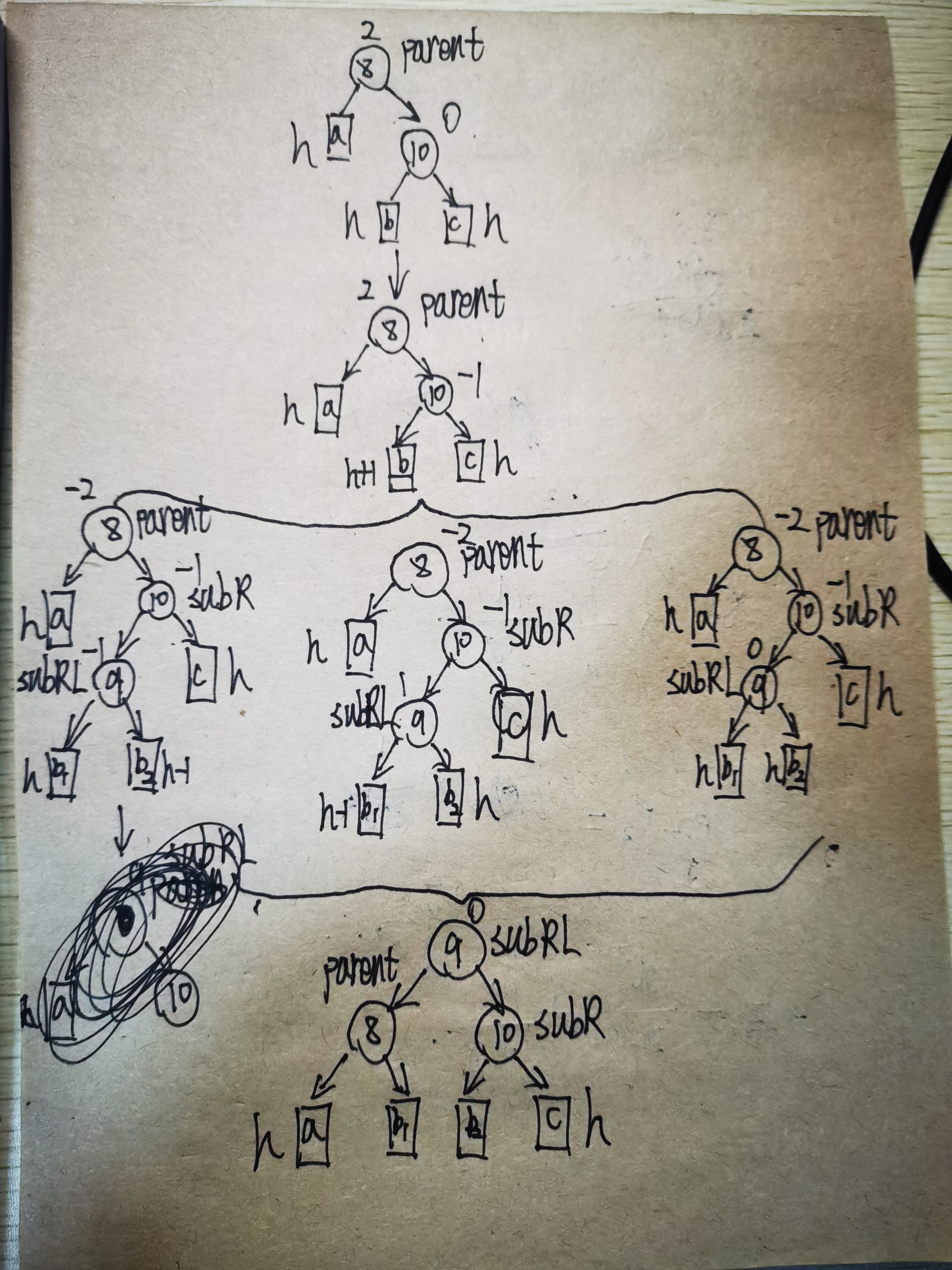
分析上述图片中的情况,我们将parent的右节点定义为subR,将subR的左节点定义为subRL,对于这个情况,我们可以根据subRL平衡因子的值将这个情形分为三种不同的情况,最终调整后的结果我们看到,subRL成为了根节点,subR成为了subRL的左节点,parent成为了subRL的右节点。
仔细观察我们发现,这种情况下的调整可以先以parent的右节点为旋转中心,进行一次右旋转,然后再以parent为旋转中心,进行一次左旋转,因此我们将这种情况称为右左双旋,满足右左双旋的条件是:parent节点的平衡因子是2,cur节点的平衡因子是-1,旋转结束后我们根据subRL节点的平衡因子的值对subRL、subR、parent的平衡因子进行赋值,因此我们可以写下如下代码:
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else if(bf==1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 1;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}插入代码如下所示
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{cout << "插入值已存在,请重新输入" << endl;return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else{assert(false);}break;}else{assert(false);}}return true;
}void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* grendParent = parent->_parent;if (subRL)subRL->_parent = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subR;}else{grendParent->_right = subR;}subR->_parent = grendParent;}parent->_bf = subR->_bf = 0;
}void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* grendParent = parent->_parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subL;}else{grendParent->_right = subL;}subL->_parent = grendParent;}subL->_bf = parent->_bf = 0;
}void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else if(bf==1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 1;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else{assert(false);}
}
AVL树的查找
AVL树的查找与二叉搜索树相同,从根节点开始查找,如果目标值大于根节点的值就走向右子树,如果目标值小于根节点的值就走向左子树,其代码如下所示:
Node* Find(const pair<K, V>& kv)
{Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){cur = cur->_left;}else if (kv.first > cur->_kv.first){cur = cur->_right;}else{return cur;}}return nullptr;
}AVL树的遍历
我们通过中序递归的方式遍历整个AVL树,其代码如下所示:
void InOrder()
{_InOrder(_root);cout << endl;
}
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_InOrder(root->_right);}AVL树的节点个数以及高度
int Height(){return _Height(_root);}int Size(){return _Size(_root);}void InOrder(){_InOrder(_root);cout << endl;}
private:int _Height(Node* root){if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}与遍历相同,我们都是通过递归的方式遍历AVL树,不同的是它的高度是通过后序遍历完成的
判断平衡
bool _IsBalanceTree(Node* root)
{if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "高度异常"<<endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}AVL树代码如下所示
#include<iostream>
using namespace std;#include<assert.h>namespace FJY
{template<class K,class V>struct AVLTreeNode{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}};template<class K,class V>class AVLTree{typedef AVLTreeNode<K, V> Node;public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{cout << "插入值已存在,请重新输入" << endl;return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else{assert(false);}break;}else{assert(false);}}return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* grendParent = parent->_parent;if (subRL)subRL->_parent = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subR;}else{grendParent->_right = subR;}subR->_parent = grendParent;}parent->_bf = subR->_bf = 0;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* grendParent = parent->_parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subL;}else{grendParent->_right = subL;}subL->_parent = grendParent;}subL->_bf = parent->_bf = 0;}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else if(bf==1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 1;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else{assert(false);}}Node* Find(const pair<K, V>& kv){Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){cur = cur->_left;}else if (kv.first > cur->_kv.first){cur = cur->_right;}else{return cur;}}return nullptr;}int Height(){return _Height(_root);}int Size(){return _Size(_root);}void InOrder(){_InOrder(_root);cout << endl;}private:int _Height(Node* root){if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_InOrder(root->_right);}bool _IsBalanceTree(Node* root){if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "高度异常"<<endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}private:Node* _root=nullptr;};
}小结
本篇博客我们重点介绍了AVL树的插入,以及其他接口的实现,通过了解AVL树的底层实现,我们将更加深入理解平衡二叉搜索树的概念,为之后学习红黑树打下了基础,后续我们将讲解map和set的底层实现,它的底层是用的红黑树完成,所以学习AVL树将为我们后面的学习打下基础
以上就是本篇博客的主要内容,如果对您有所帮助的话,记得点赞、评论、关注加转发,您的支持就是我创作的最大动力
相关文章:
——AVL树(平衡二叉搜索树))
数据结构(五)——AVL树(平衡二叉搜索树)
目录 前言 AVL树概念 AVL树的定义 AVL树的插入 右旋转 左旋转 左右双旋 右左双旋 插入代码如下所示 AVL树的查找 AVL树的遍历 AVL树的节点个数以及高度 判断平衡 AVL树代码如下所示 小结 前言 前面我们在数据结构中介绍了二叉搜索树,其中提到了二叉搜…...

Linux文件传输:让数据飞起来!
一、前置任务 为了便于实验,我用母盘的虚拟机克隆出两台虚拟机来模拟两台主机进行文件传输 查询两台主机的IP BL1 192.168.163.130/24 BL2 192.168.88.129/24 二、文件传输 scp命令 不填选项正常显示进度的传输-q静默传输-r递归传输(用于传输目录及目…...

repo仓库文件清理
1. repo 仓库内文件清理 # 清理所有Git仓库中的项目 repo forall -c git clean -dfx # 重置所有Git 仓库中的项目 repo forall -c git reset --hard 解释: repo forall -c git clean -dfx: repo forall 是一个用于在所有项目中执行命令的工具。-c 后…...

MyBatis-Plus 的 FieldStrategy 属性
前几天做个需求的时候,有几个字段在更新的时候,可能为空。想着MyBatis-Plus有注解可以直接使用,就找寻了一下。此处记录一下。我用的MyBatis-Plus的版本是 3.5.1。版本之间对于 TableField 中的方法定义有些区别,但大体相差不大。…...

解锁塔能科技,开启工厂绿色转型与可持续发展双引擎
在全球积极推进可持续发展的大背景下,能源的高效利用与节能减排,已成为各行各业迈向高质量发展进程中无法回避的核心任务。工厂作为能源消耗大户与污染排放重点源头,其绿色转型迫在眉睫,这不仅关乎企业自身的长远发展,…...

c++进阶--智能指针
大家好,今天我们来学习一下c中的智能指针部分。 智能指针的使⽤及其原理 1. 智能指针的使⽤场景分析 下⾯程序中我们可以看到,new了以后,我们也delete了,但是因为抛异常导,后⾯的delete没有得到执⾏,所以…...

五种常用的web加密算法
文章目录 五种常用Web加密算法实战及原理详解1. AES (高级加密标准)原理详解应用场景实战代码(Node.js) 2. RSA (非对称加密)原理详解应用场景实战代码(Node.js) 3. SHA-256 (安全哈希算法)原理详解应用场景实战代码(浏…...

LeetCode 题目 「二叉树的右视图」 中,如何从「中间存储」到「一步到位」实现代码的优化?
背景简介 在 LeetCode 的经典题目 「二叉树的右视图」 中,我们需要返回从右侧看一棵二叉树时所能看到的节点集合。每一层我们只能看到最右边的那个节点。 最初,我采用了一个常规思路:层序遍历 每层单独保存节点值 最后提取每层最后一个节…...

MySQL——存储过程、索引
一、存储过程 1、存储过程使用的场景 例如:有一个购物网站,要验证查询商品的性能,测试之前肯定要准备大量的测试数据,如果是通过 执行 insert 语句一条一条进行插入,效率很低。这种情况下,写一个存储过程…...

【项目管理】第9章 项目范围管理
相关文档,希望互相学习,共同进步 风123456789~-CSDN博客 (一)知识总览 项目管理知识域 知识点: (项目管理概论、立项管理、十大知识域、配置与变更管理、绩效域) 对应:第6章-第19章 (二)知识笔记 第9章 项目范围管理 1.管理基础 1.1 产品范围…...

无人机隐身技术难点要点!
全频段雷达隐身 频段覆盖挑战:传统隐身材料(如铁氧体、掺杂半导体)多针对特定频段(如X波段),难以应对米波至毫米波的宽频段探测。 低频段突破:低频雷达(如米波雷达)波长…...

gerrit配置及使用git-lfs
gerrit服务器端配置 下载git-lfs插件 登录Dashboard [Jenkins] (gerritforge.com),下载对应版本的插件 配置gerrit 将下载的lfs.jar插件放到${GERRIT_SITE}/plugins/下面为所有仓库启用git-lfs 此步骤需要修改 All-projects 仓库配置,步骤如下 1、克隆仓…...

基于DNS的负载均衡和反向代理负载均衡
基于 DNS 的负载均衡和反向代理负载均衡有一些相似之处,但实际上它们存在诸多区别,主要体现在以下几个方面: 工作原理 DNS 负载均衡:通过在 DNS 服务器中为同一主机名配置多个 IP 地址,DNS 服务器根据一定的算法&…...

Windows10 ssh无输出 sshd服务启动失败 1067报错 公钥无法认证链接 解决办法
背景描述 最近突然发现windows 10的ssh服务好像挂了,在系统设置-可选功能那里反复重新安装还是报错。命令行输入ssh按回车无输出(正常情况下应该输出一堆参数说明),但是Get-Command ssh 又可以找到system32下的ssh程序。任务管理…...
、修改图书属性接口(XML 实现))
【图书管理系统】深入解析基于 MyBatis 数据持久化操作:全栈开发图书管理系统:查询图书属性接口(注解实现)、修改图书属性接口(XML 实现)
查询图书属性接口 约定前后端交互接口 约定前后端交互接口,进入修改页面,需要显示当前图书的信息; 请求 /book/queryBookById?bookId25 参数 无 响应 { "id": 25, "bookName": "图书21", "…...
)
消息队列(IPC技术)
目录 一、Linux 中主要的进程间通信方式如下: 二、消息队列函数 (1)msgget函数 功能概述 函数原型 参数解释 返回值 示例 结果 问题 (2) msgsnd函数 功能概述 函数原型 参数说明 返回值 示例 结果 (3࿰…...

分支语句和循环语句
什么是语句? C语言中由一个分号;隔开的就是一条语句。 比如: printf("haha");12;分支语句 if语句 if语句的语法结构: if(表达式)语句;if(表达式)语句1; else语句2;//多分支 if(表达式1)语句1; else if(表达式2)语句2; else语句3;在C语言…...

MySQL基础 [八] - 事务
目录 前言 什么是事务 事务的版本支持 事务的提交方式 事务的相关演示 并行事务引发的问题 脏读 dirty read 不可重复读 non-repeatable read 幻读 phantom read 事务的隔离级别 查看与设置隔离级别 读未提交(Read Uncommitted) 读提交&…...

深入理解Java反射
反射(Reflection)是Java语言的一个强大特性,它允许程序在运行时动态地获取类的信息并操作类或对象的属性、方法和构造器。就是在获取运行时的java字节码文件,通过各种方法去创建对象,反射是Java被视为动态语言的关键特性之一。 反射其实就是…...

【UE】渐变框材质
效果 步骤 新建一个材质,这里命名为“M_GlowingBorder”,打开“M_GlowingBorder”后,设置材质域为“用户界面”,混合模式为“半透明” 添加如下节点: 代码: Begin Object Class/Script/UnrealEd.Materia…...

2025年第十八届“认证杯”数学中国数学建模网络挑战赛【ABCD题】思路分析
首先,需要理解用户的需求。问题1需要数学模型来确定小行星的相对距离,而问题2需要预测短期轨道并计算特定时间的观测角度。这两个问题都需要结合天文学和数学建模的知识,涉及到轨道力学和几何定位的方法。 接下来,查阅提供的搜索…...

JavaScript 性能优化:突破瓶颈的实战指南
一、引言 在现代 Web 应用和 Node.js 服务端开发中,JavaScript 已成为核心编程语言。随着应用复杂度提升,性能问题愈发凸显。高延迟、卡顿甚至崩溃等现象,不仅影响用户体验,还可能导致业务流失。深入理解 JavaScript 性能瓶颈并…...

HarmonyOS:组件布局保存至相册
一,需求背景 有这样一个需求,将页面上的某个自定义组件以图片的形式保存至相册。 二,需求拆解 根据需求分析,可将需求拆解成两步: 1,将组件转换成图片资源; 2,将图片保存到相册…...

【langchain库名解析】
目录 一、from langchain_openai import ChatOpenAI 1. 核心功能 2. 典型使用场景 场景 1:直接生成对话回复 场景 3:流式输出(逐词显示结果) 3. 与其他 LangChain 组件的协同 结合提示模板(PromptTemplate&#…...

629SJBH图书管理系统设计与实现
一、 绪论 (一)课题的提出、现状及研究意义 图书馆是文献情报中心,是为教学和科研服务的学术性机构。它履行搜集、加工、存贮和传播知识信息的职能,与各系资料室互为补充,共同承担为教学和科研提供文献情报资料保障的…...

2025 年“认证杯”数学中国数学建模网络挑战赛 A题 小行星轨迹预测
近地小行星( Near Earth Asteroids, NEAs )是轨道相对接近地球的小行 星,它的正式定义为椭圆轨道的近日距不大于 1.3 天文单位( AU )的小行星。 其中轨道与地球轨道最近距离小于 0.05A 且直径大于 140 米的小行星被…...

PhotoShop学习09
1.弯曲钢笔工具 PhotoShop提供了弯曲钢笔工具可以直观地创建路径,只需要对分段推拉就能够进行修改。弯曲港币工具位于工具面板中的钢笔工具里,它的快捷键为P。 在使用前,可以把填充和描边选为空颜色,并打开路径选项,勾…...

远程管理命令:关机和重启
关机/重启 序号命令对应英文作用01shutdown 选项 时间shutdown关机 / 重新启动 一、shutdown shutdown 命令可以安全关闭 或者 重新启动系统。 选项含义-r重新启动 提示: 不指定选项和参数,默认表示 1 分钟之后 关闭电脑远程维护服务器时࿰…...

用Perl和HTTP::Tiny库的爬虫
HTTP::Tiny是Perl的一个轻量级HTTP客户端,适合简单的请求,但不像LWP那样功能全面,不过对于基本需求应该足够了。 首先,我需要熟悉HTTP::Tiny的基本用法。比如如何发起GET请求,设置user-agent,处理响应。用…...

MPP 架构解析:原理、核心优势与对比指南
一、引言:大数据时代的数据处理挑战 全球数据量正以指数级增长。据 Statista 统计,2010 年全球数据量仅 2ZB,2025 年预计达 175ZB。企业面临的核心挑战已从“如何存储数据”转向“如何快速分析数据”。传统架构在处理海量数据时暴露明显瓶颈…...

2025.04.10-拼多多春招笔试第三题
📌 点击直达笔试专栏 👉《大厂笔试突围》 💻 春秋招笔试突围在线OJ 👉 笔试突围OJ 03. 数字重排最大化问题 问题描述 LYA是一位专业的数字设计师。她手中有两个数字序列 s 1 s_1...

前端-vue2核心
官网网址Vue2 安装 — Vue.js 搭建环境 第一种方式(刚开是接触Vue) 我们看官网,可以直接在script引入vue版本。这里有两个版本,开发版和生产版本。我们两个都下载。 然后创建一个项目,将下载的生产版本和开发版本粘…...
)
基于springboot的“协同过滤算法的高考择校推荐系统”的设计与实现(源码+数据库+文档+PPT)
基于springboot的“协同过滤算法的高考择校推荐系统”的设计与实现(源码数据库文档PPT) 开发语言:Java 数据库:MySQL 技术:springboot 工具:IDEA/Ecilpse、Navicat、Maven 系统展示 系统功能结构图 局部E-R图 系统…...

制作前的关键筹备:考试考核系统之核心要点
明确系统使用目的 制作考试考核系统前,企业需明确系统使用目的,这是开发基石,不同目的决定系统功能特性。用于员工培训考核时,系统要与培训内容结合,能生成相应考题,检验员工知识掌握程度,具备…...

【动手学深度学习】现代卷积神经网络:ALexNet
【动手学深度学习】现代卷积神经网络:ALexNet 1,ALexNet简介2,AlexNet和LeNet的对比3, AlexNet模型详细设计4,AlexNet采用ReLU激活函数4.1,ReLU激活函数4.2,sigmoid激活函数4.3,为什…...

Linux自启动脚本 systemctl
1.编写好脚本 #!/bin/bash /home/china/Linux/code/a.out2. 创建 Systemd 服务文件 sudo gedit /etc/systemd/system/my_script.service3.编写服务配置 将以下内容写入文件(根据需求修改字段): [Unit] DescriptionMy Custom Shell Script…...

2024年KBS SCI1区TOP:信息增益比子特征分组赋能粒子群算法ISPSO,深度解析+性能实测
目录 1.摘要2.信息度量3.改进策略4.结果展示5.参考文献6.代码获取 1.摘要 特征选择是机器学习中的关键预处理步骤,广泛应用于实际问题。尽管粒子群算法(PSO)因其强大的全局搜索能力被广泛用于特征选择,但要开发一种高效的PSO方法…...

餐饮厨房开源监控安全系统的智能革命
面对日益严格的合规要求和消费者对卫生的信任危机,传统人工监督已力不从心:卫生死角难发现、违规操作难追溯、安全隐患防不胜防。如何让后厨更透明、更安全、更可信?餐饮厨房视频安全系统横空出世!这套系统融合实时监控与AI技术&a…...

Ansys Electronics 变压器 ACT
你好, 在本博客中,我将讨论如何使用 Ansys 电子变压器 ACT 自动快速地设计电力电子电感器或变压器。我将逐步介绍设计和创建电力电子变压器示例的步骤,该变压器为同心组件,双绕组,采用正弦电压激励,并应用…...

Redis与Lua原子操作深度解析及案例分析
一、Redis原子操作概述 Redis作为高性能的键值存储系统,其原子性操作是保证数据一致性的核心机制。在Redis中,原子性指的是一个操作要么完全执行,要么完全不执行,不会出现部分执行的情况。 Redis原子性的实现原理 单线程模型&a…...

Shell 脚本开发从入门到实战
第1章:什么是 Shell 与 Shell 脚本? 一、Shell 是什么? Shell 是一个命令解释器,是你在 Linux 里敲命令的地方。你平时用的命令如 cd、ls、echo,其实都由 Shell 来解析执行。最常见的 Shell 是 Bash,绝大…...

宇视设备视频平台EasyCVR打造智慧酒店安防体系,筑牢安全防线
一、需求背景 酒店作为人员流动频繁的场所,对安全保障与隐私保护有着极高的要求。为切实维护酒店内部公共区域的安全秩序,24小时不间断视频监控成为必要举措。通常情况下,酒店需在本地部署视频监控系统以供查看,部分连锁酒店还希…...

深度解读分销小程序商城源码系统:从搭建到运营的关键指南
在移动互联网浪潮的席卷下,电商领域持续变革与创新。分销小程序商城凭借其独特优势,如依托社交平台流量、便捷的购物体验、高效的分销推广模式等,成为众多企业和创业者开展线上业务的热门选择。深入了解分销小程序商城源码系统,从…...

BeeWorks:打造安全可控的企业内网即时通讯平台
在数字化办公时代,企业对即时通讯工具的需求日益增长,尤其是对数据安全和隐私保护有严格要求的行业,如金融、政府、医疗等。BeeWorks 作为一款专注于内网部署的即时通讯软件,凭借其卓越的安全性、稳定性、丰富的功能以及全面的信创…...

微信小程序开发:废品回收小程序-功能清单
用户端:便捷体验,触手可及 废品百科与估价指南:平台以直观的方式展示各类废品的分类标准与实时市场价格,让用户轻松掌握废品价值,决策更从容。 一键预约,轻松回收:用户只需轻触屏幕,…...

【Grok 大模型深度解析】第一期:技术溯源与核心突破
一、Grok的技术基因:从Transformer到混合架构的演进 1.1 Transformer架构的局限性 2017年Google提出的Transformer架构彻底改变了自然语言处理领域,其自注意力机制(Self-Attention)在长序列建模上表现优异。然而,随着模型规模的增大,传统Transformer暴露出以下问题: 计…...

性能比拼: Redis vs Memcached
本内容是对知名性能评测博主 Anton Putra Redis vs Memcached Performance Benchmark 内容的翻译与整理, 有适当删减, 相关指标和结论以原作为准 在本视频中,我们将对比 Redis 和 Memcached。我会介绍一些功能上的不同,但主要关注 性能。 首先…...

Mujoco xml actuator
actuator general(通用执行器)motor(电机执行器)position(位置伺服)velocity(速度伺服)intvelocity(积分速度伺服)damper(主动阻尼器)…...

Mybatis Plus分页查询返回total为0问题
概述 最近开发公司新项目,使用 Mybatis Plus 分页,发现总数和总页数为0,在此记录问题和解决方案。 添加 MybatisPlusConfig /*** author: lanys* version: 1.0* 创建时间:2025年4月9日 14:24:40* Description: MybatisPlus分页…...

多卡分布式训练:torchrun --nproc_per_node=5
多卡分布式训练:torchrun --nproc_per_node=5 1. torchrun 实现规则 torchrun 是 PyTorch 提供的用于启动分布式训练作业的实用工具,它基于 torch.distributed 包,核心目标是简化多进程分布式训练的启动和管理。以下是其主要实现规则: 进程启动 多进程创建:torchrun 会…...
