树和图论(详细整理，简单易懂！)

树和图论

树的遍历模版

#include <iostream>
#include <cstring>
#include <vector>
#include <queue>  // 添加queue头文件  
using namespace std;const int MAXN = 100;  // 假设一个足够大的数组大小
int ls[MAXN], rs[MAXN];  // 定义左右子树数组//后序遍历
void dfs(int x) {if(ls[x]) dfs(ls[x]);if(rs[x]) dfs(rs[x]);cout << x << ' ';
}//层序遍历
void bfs() {queue<int> q;//起始节点入队q.push(1);//队列不为空则循环while(q.size()) {//访问队列元素xint x = q.front();//取出队列元素q.pop();//一系列操作cout << x << " ";if(ls[x]) q.push(ls[x]);if(rs[x]) q.push(rs[x]);}
}
int main() {int n;cin >> n;for(int i = 1; i <= n; i++) {cin >> ls[i] >> rs[i];}dfs(1);cout << endl;bfs();return 0;
}

最近公共祖先LCA

本质是一个dp,类似于之前的ST表

fa[i][j]表示i号节点，向上走2^j所到的节点，当dep[i]-2^j>=1时fa[i][j]有效

又因为我们知道2^(j-1) + 2^(j-1)= 2^j， i的2^（j-1） 级祖先的2^(j-1)级祖先 就是i的2^j级祖先。

形象理解：

我们要求x(5号节点)与y(10号节点)的 LCA

倍增的时候，我们发现y的深度比x的深度要小，于是现将y跳到8号节点，使他们深度一样：

这个时候，x和y的深度就相同了，于是我们按倍增的方法一起去找LCA

我们知道n（10）之内最大的二的次方是8，于是我们向上跳8个单位，发现跳过了。

于是我们将8/2变成4，还是跳过了。

再将4/2变成2，跳到了0号节点。

虽然这时跳到了LCA,但是如果直接if（x==y）就确定的话，程序无法判断是刚好跳到了还是跳过了，应为跳过了x也等于y

于是我们需要刚好跳到LCA的儿子上，然后判断if（x的爸爸==y的爸爸）来确定LCA

由于每一个数都可以分解为几个2^n的和（不信自己试），所以他们一定会跳到LCA的儿子上

于是我们就找到了LCA啦！

代码模版：

int lca(int x,int y){//x喜欢跳。。。//如果x深度比y小，交换x和y 保证x深度大if(dep[x]<dep[y]) swap(x,y); //贪心:i从大到小 //x向上跳的过程中，保持dep[x]>=dep[y],深度不能超过y for(int i=20;i>=0;i--){if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];} //x跳完 此刻x和y的dep相同//如果发现相遇了 那么就是这个点if(x==y) return x;//(int)(log(n)/log(2))就是n以内最大的2的次方，从最大的开始倍增for(int i=(int)(log(n)/log(2));i>=0;i--) //如果x和y爸爸不想同 则没有找到//整个跳跃过程中,保持x!=y,不用x=y判断if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];//x和y一起向上跳 return fa[x][0];//返回他们的爸爸，即是LCA  
}

可是在写LCA之前，我们还得进行预要处理些什么呢？

1.每一个点的深度，以便到时候判断

2.每一个点2^i级的祖先，以便到时候倍增跳

于是我们用一个dep数组来记录每一个点的深度，再用一个fa[i][j]表示节点i的2^j级祖先

void dfs(int x,int p){dep[x]=dep[p]+1;//x的深度是他父亲的深度+1 fa[x][0]=p;//2^0是1，x向上一个的祖先就是他爸爸for(int i=1;i<=20;i++)	fa[x][i]=fa[fa[x][i-1]][i-1];//父节点再向上2^i-1 for(const auto &y : g[x]){ //枚举x所有儿子if(y==p) continue;//如果不是他爸爸 继续dfsdfs(y,x);} 
}

树的重心

指对于某个点，将其删除后，可以是的剩余联通块的最大值最小的点（剩余的若干子树的大小最小）

性质：

• 中心若干棵子树大小一定**<=n/2**；除了重心以外的所有其他节点，都必然存在一棵节点个数>n/2的子树
• 一棵树至多两个重心，如果存在，则必然相邻；将连接两个重心的边删除后，一定划分为两棵大小相等的树
• 树中所有点到某个点的距离和中，到重心的距离和是最小的
• 两棵树通过一条边相连，重心一定在较大的一棵树一侧的连接点与原重心之间的简单路径上。两棵树大小相同，则重心就是两个连接点。

如何求解重心？

跑一遍dfs，如果mss[x]<=n/2,则x是重心，反之不是。

void dfs(int x,int fa){//初始化mss/sz数组sz[x]=1,mss[x]=0;for(const auto& y:g[x]){if(y==fa) continue;dfs(y,x);sz[x]+=sz[y];mss[x]=max(mss[x],sz[y]);}//后序位置比较mss大小并判断mss[x]=max(mss[x],n-sz[x]);if(mss[x]<=n/2) v.push_back(x);
}

树的直径

树上任意两节点之间最长的简单路径即为树的「直径」。

直径由u,v决定,若有一条直径(u,v)满足 : **1)**u和v度数均为1；2）在任意一个点为根的树上，u和v中必然存在一个点作为最深的叶子节点。

如何求解直径？

跑两遍dfs：以任意节点为根的树上跑一次dfs求所有点的深度，选最大的点作为u，再以u为根拍一次dfs，最深的点为v，路径上点的个数为树的dep[v]+1(根节点深度为0)/ dep[v](根节点深度为1)

树上差分

差分的思想方法：

如果有一个区间内的权值发生相同的改变的时候，我们可以采用差分的思想方法，而差分的思想方法在于不直接改变区间内的值，而是改变区间[ L , r ] 对于 区间 [ 0, L - 1 ] & 区间[ r + 1, R]的 相对大小关系

差分，可以当做前缀和的逆运算。既然是逆运算，运算方法自然就是相反的了。定义差分数组
$$dif{f}_i=a_i-a_{i-1}$$

compare：

原数列	9	4	7	5	9
前缀和	9	13	20	25	34
差分数组	9	-5	3	-2	4
前缀和的差分数组	9	4	7	5	9
查分数组的前缀和	9	4	7	5	9

树上差分，就是利用差分的性质，对路径上的重要节点进行修改（而不是暴力全改），作为其差分数组的值，最后在求值时，利用dfs遍历求出差分数组的前缀和，就可以达到降低复杂度的目的。

这里差分的优点就非常明显了：

• 算法复杂度超低
• 适用于一切 连续的 “线段”

这里所谓的线段可以是一段连续的区间，也可以是路径

点差分:

模版题目：给出一棵 n 个点的树，每个点点权初始为 0，现在有 m 次修改，每次修改给出 x,y，将 x,y 简单路径上的所有点的点权 +d，问修改完之后每个点的点权。

将序列差分转移到树上：比如我们要对 x,y 的路径上的点统一加上 d。

涉及到的点有：x,h,b,f,y因此对于点 a 我们不能有影响，操作方案就是 b（回溯时左右加了两次）的点权减去 d，a 的点权减去 d。

最后我们对整棵树做一遍 dfs，将所有点的点权变为其子树（含自己）内所有点的点权，这个操作仿照求每个点子树的 Size 就可以完成了。

模版代码：

同样需要lca的两个模版函数,并添加:

dlt[i]:存放每个点经过的次数

void dfs1(int x){for(int i=0;i<v[x].size();i++){int u=v[x][i];if(u!=fa[x][0]){dfs1(u);//回溯dlt[x]+=dlt[u];}}return;
}
int main() {cin>>n>>k;maxx=log2(n); for(int i=1;i<n;i++){int a,b;cin>>a>>b;v[a].push_back(b),v[b].push_back(a); }dfs(1,0);//k次询问 处理k条路径 for(int i=1;i<=k;i++){int a,b;cin>>a>>b;dlt[a]++,dlt[b]++;int c=lca(a,b);dlt[c]--,dlt[fa[c][0]]--;}dfs1(1);for(int i=1;i<=n;i++) cout<<dlt[i]<<" ";return 0;
}

美妙的例题：

[P3258 JLOI2014] 松鼠的新家 - 洛谷 (luogu.com.cn)

边差分：

模版题目：给出一棵 n个点的树，每条边边权初始为 0，现在有 m 次修改，每次修改给出 x,y将 x,y简单路径上的所有边边权 +d，问修改完之后每条边的边权。

首先我们需要一种叫做**“边权转点权”的方法，就是对于每个点我们认为其点权代表这个点与其父节点之间的边的边权**，对于每条边我们认为其边权是这条边所连两个点中深度较大的点的点权，根节点点权无意义。

还是修改 x,y路径上的边，还是这张图：

涉及的边/点：x,h,f,y,对于点 b 我们不能有影响，操作方案就是 b（回溯时左右加了两次 实则不变）的点权（b与父亲节点的边权）减去 2d。

同样的做完之后一遍 dfs 求一下每个点的点权即可。

图的遍历模版

DFS:

bitset<N> vis;//vis[i]=true说明i点已经走过
void dfs(int x){vis[x]=true;for(const auto& y:g[x]){if(vis[y]) continue;dfs(y);}
}

BFS:

维护一个queue，通常用于求边权相等情况下的最短距离

bitset<N> vis;
queue<int> qu;
void bfs() {  qu.push(1);//从1开始while (!qu.empty()) {  int x = qu.front();  qu.pop();  if (vis[x]) continue;  // 避免重复处理  vis[x] = true;         // 标记已访问  for (const auto& y : g[x]) {  if (!vis[y]) qu.push(y);    // 未访问的邻居入队  }  }  
}  

例题1：帮派弟位

找到每个节点i 的子树大小siz[i]

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+9;
vector<int> g[N];
int siz[N];//存放包含自己在内的子树节点个数
void dfs(int x,int p){siz[x]=1;//叶子如果设为0则对父节点的size毫无影响for(const auto &y:g[x]){if(y==p) continue;dfs(y,x);siz[x]+=siz[y];}
}
struct Node{int id,siz;//rule:主要按 siz 降序（siz > u.siz） siz 相同，则按 id 升序（id < u.id）bool operator < (const Node &u)const {return siz==u.siz?id<u.id:siz>u.siz;}
};int main()
{int n,m;cin>>n>>m;for(int i=1;i<n;i++){int r,l;cin>>l>>r;//存储有向树g[r].push_back(l);}dfs(1,0);//v存储每个编号的手下人数多少vector<Node> v;//vector下标必须从0开始i=0存for(int i=0;i<n;i++) v.push_back({i,siz[i]-1});sort(v.begin(),v.end());for(int i=0;i<n;i++) if(v[i].id==m) cout<<i+1<<endl;return 0;
}

例题2: 可行路径的方案数

计算从节点 1 到节点 n 的最短路径数量

理解：

• “当前路径” = 从城市1到 x 的已知最短路径 + 边 x→y。
• 这条路径的长度是 d[x] + 1（因为所有边权为1，即每走一步距离+1）。

1. 如果 d[x] + 1 < d[y]：
   • 发现了一条更短的路径到 y。
   • 更新 d[y] = d[x] + 1，并重置 dp[y] = dp[x]（因为旧路径不再有效）。
   • 将 y 加入队列，继续探索。
2. 如果 d[x] + 1 == d[y]：
   • 找到了一条等长的最短路径到 y。
   • 累加方案数：dp[y] += dp[x]（模 p 防止溢出）。
   • 无需重复入队（因为距离未变，BFS保证先到的最短路径已处理）。
3. 如果 d[x] + 1 > d[y]：
   • 当前路径比已知最短路径长，直接跳过。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9;
const int p = 1e9 + 7;
vector<int> g[N];
// d[]表示从索引值城市到城市1的距离；dp[]表示从索引值城市到城市1最近的路径
int d[N], dp[N];
void bfs() {bitset<N> vis;queue<int> qu;qu.push(1);memset(d, 0x3f, sizeof d); //给每个城市最近距离初始化为无穷d[1] = 0;//1到第一个城市的距离为0dp[1] = 1; //到第一个城市方案数为1while(!qu.empty()) {//访问并取出队头 判断并标记为visitedint x = qu.front();qu.pop();if(vis[x]) continue;vis[x] = true;//找下一个城市y 判断d[y]与d[x]+1的关系for(const auto & y : g[x]) {//从城市1到城市y的距离比之前走过的远,不考虑if(d[x] + 1 > d[y]) continue;//找到另一条最短路径，累加方案数if(d[x] + 1 == d[y]) dp[y] = dp[y] + dp[x] % p;//找到一条更短的经过x y的路else 	d[y] = d[x] + 1, dp[y] = dp[x];qu.push(y);}}
}
int main() {int n, m;cin >> n >> m;//双向图for(int i = 1; i <= m; i++) {int a, b;cin >> a >> b;g[a].push_back(b);g[b].push_back(a);}bfs();cout << dp[n] << endl;return 0;
}

实例：

1 -- 2 -- 3  \   /  4

bfs过程：

1. 从城市1出发，d[1]=0，dp[1]=1。

2. 遍历1的邻居

   {2, 4}
   

   • 更新 d[2]=1，dp[2]=1；d[4]=1，dp[4]=1。

3. 处理城市2：

   • 邻居

     {1, 3, 4}
     

     • 1已访问（d[1]=0），跳过。
     • 到3的“当前路径”长度 d[2]+1=2，更新 d[3]=2，dp[3]=1。
     • 到4的“当前路径”长度 d[2]+1=2，但 d[4]=1（更短），跳过。

4. 处理城市4：

   • 邻居

     {1, 2}
     

     • 1已访问，跳过。
     • 到2的“当前路径”长度 d[4]+1=2，但 d[2]=1（更短），跳过。

5. 处理城市3：

   • 邻居 {2}，已处理。

最小生成树Kruskal

与Prim算法不同，该算法的核心思想是归并边，而Prim算法的核心思想是归并点。若边数远少于完全图，Kruskal比Prim算法更高效。

思想回顾：

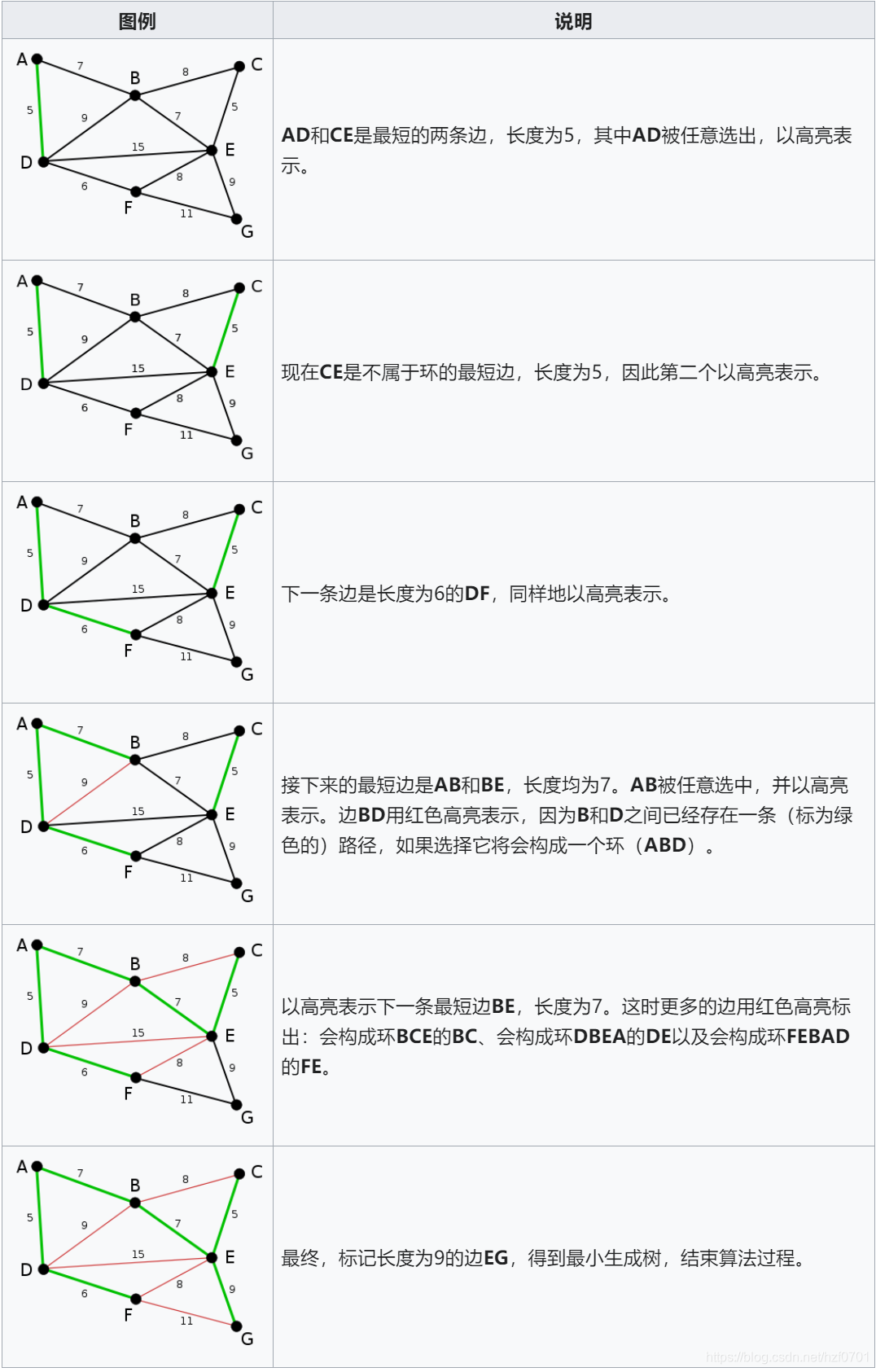
步骤：

1. 按照所有边权排序
2. 从小到大遍历所有边(u，v),如果已联通就跳过，否则就选中(u,v),将其连通。（用到并查集）

模版题代码：旅行销售员

走完N个城市，每公里消耗1升油，找出所需油箱的最小容量。

#include <iostream>  
#include <vector>  
#include <algorithm>  using namespace std;  
using ll = long long;  // 使用长整型存储权值  // 边结构体：起点x、终点y、权值c  
struct Edge {  ll x, y, c;  // 重载<运算符，按权值升序排序  bool operator<(const Edge& u) const {  return c < u.c;  }  
};  // 并查集：查找根节点（带路径压缩）
//目标：确定哪些节点属于同一个连通分量，它并不关心边的方向性
int root(vector<int>& pre, int x) {  return pre[x] == x ? x : pre[x] = root(pre, pre[x]);  
}  void solve() {  int n, m;  // 节点数、边数  cin >> n >> m;  // 初始化并查集  vector<int> pre(n + 1);  for (int i = 1; i <= n; ++i) {  pre[i] = i;  // 初始时每个节点的父节点是自己  }  // 读取所有边  vector<Edge> es;  for (int i = 1; i <= m; ++i) {  ll x, y, c;  cin >> x >> y >> c;  es.push_back({x, y, c});  }  // 按边权升序排序  sort(es.begin(), es.end());  ll res = 0;  // 记录MST中的最大边权  for (const auto& edge : es) {  int x = edge.x;  int y = edge.y;  ll c = edge.c;  // 若x和y不连通，则合并它们  if (root(pre, x) != root(pre, y)) {  res = max(res, c);  // 更新最大边权  pre[root(pre, x)] = root(pre, y);  // 合并操作  }  }  cout << res << endl;  // 输出结果  
}  int main() {  int T = 0;  // 测试数据组数  cin >> T;  while (T--) {  solve();  // 处理每组数据  }  return 0;  
}

最小生成树Prim

思想回顾：

与dijkstra很像，逐步扩大树中所含顶点的数目，直到遍及连通图的所有顶点。下面描述我们假设N = ( V , E ) 是连通网，T E 是N 上最小生成树中边的集合。

1. 每次找出不再mst中且d[]最小的点x，d[x]就是选中的那条边的边权。
2. 将x加入mst，并更新其所有出点y，d[y]=min(d[y],w) //w为x到y的距离
3. 如果d[y]变小，就加入到优先队列中作为可能的拓展点

mst使用bitset数组实现即可

代码模版题：

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1E6 + 5;
ll n, m, inf = 1e9;
struct Edge {ll x, w;bool operator <(const Edge&u)const {return w > u.w; //小根堆}
};
//邻接表
vector<Edge>g[N];
//记录从起点（节点1）到各个节点的最小权重
ll d[N];
ll Prim() {//小根堆priority_queue<Edge>pq;bitset<N>vis;pq.push({1, d[1] = 0});ll res = 0;while(pq.size()) {//访问并取出元素x 判断并标记为visited//x为不在mst且权重最小的边ll x = pq.top().x;pq.pop();if(vis[x])continue;vis[x] = true;//更新mst最小权重总和res = max(res, d[x]);//遍历x所有邻接节点for(const auto & temp : g[x]) {ll y = temp.x;ll w = temp.w;//比较w和d[y] w 更小则更新d[y]if(w < d[y])pq.push({y, d[y] = w});}}return res;
}
void solve() {cin >> n >> m;//每次clear g[N]for(int i = 1; i <= n; i++)g[i].clear(), d[i] = inf;while(m--) {ll x, y, w;cin >> x >> y >> w;//输入带权值的双向边模版g[x].push_back({y, w});g[y].push_back({x, w});}cout << Prim() << endl;
}
int main() {int t;cin >> t;while(t--)solve();return 0;
}