当前位置：首页 > news >正文

http://noi.openjudge.cn/_2.5基本算法之搜索_1804:小游戏

news 来源：原创 2025/8/23 15:14:06

文章目录

- 题目
- 深搜代码
- 宽搜代码
- 深搜数据
- 演示图
- 总结

题目

1804:小游戏
总时间限制: 1000ms 内存限制: 65536kB
描述
一天早上，你起床的时候想：“我编程序这么牛，为什么不能靠这个赚点小钱呢？”因此你决定编写一个小游戏。游戏在一个分割成w * h个正方格子的矩形板上进行。如图所示，每个正方格子上可以有一张游戏卡片，当然也可以没有。当下面的情况满足时，我们认为两个游戏卡片之间有一条路径相连：路径只包含水平或者竖直的直线段。路径不能穿过别的游戏卡片。但是允许路径临时的离开矩形板。下面是一个例子：
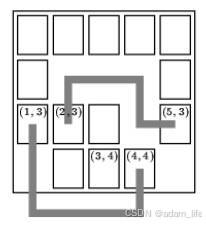
在这里插入图片描述
这里在 (1, 3)和 (4, 4)处的游戏卡片是可以相连的。而在 (2, 3) 和 (3, 4) 处的游戏卡是不相连的，因为连接他们的每条路径都必须要穿过别的游戏卡片。你现在要在小游戏里面判断是否存在一条满足题意的路径能连接给定的两个游戏卡片。
输入
输入包括多组数据(不多于10组)。一个矩形板对应一组数据。每组数据包括的第一行包括两个整数w和h (1 <= w, h <= 75)，分别表示矩形板的宽度和长度。下面的h行，每行包括w个字符，表示矩形板上的游戏卡片分布情况。使用‘X’表示这个地方有一个游戏卡片；使用空格表示这个地方没有游戏卡片。
之后的若干行上每行上包括4个整数x1, y1, x2, y2 (1 <= x1, x2 <= w, 1 <= y1, y2 <= h)。给出两个卡片在矩形板上的位置（注意：矩形板左上角的坐标是(1, 1)）。输入保证这两个游戏卡片所处的位置是不相同的。如果一行上有4个0，表示这组测试数据的结束。
如果一行上给出w = h = 0，那么表示所有的输入结束了。
输出
对每一个矩形板，输出一行“Board #n:”，这里n是输入数据的编号。然后对每一组需要测试的游戏卡片输出一行。这一行的开头是“Pair m: ”，这里m是测试卡片的编号（对每个矩形板，编号都从1开始）。接下来，如果可以相连，找到连接这两个卡片的所有路径中包括线段数最少的路径，输出“k segments.”，这里k是找到的最优路径中包括的线段的数目；如果不能相连，输出“impossible.”。
每组数据之后输出一个空行。
样例输入
5 4
XXXXX
X X
XXX X
XXX
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0
0 0
样例输出
Board #1:
Pair 1: 4 segments.
Pair 2: 3 segments.
Pair 3: impossible.

深搜代码

#include <bits/stdc++.h>
using namespace std;
struct point{int x,y,//出发行列 d,//方向 num;//线段数 
};
bool k[100][100];//标记是不是牌， 
int r,c,//地图行列 sx,sy,tx,ty, //始发和终点位置 d[4][2]={{0,-1},{-1,0},{0,1},{1,0}},//左上右下四个方向的行列变化 num[100][100];//每个点四个方向的最少线段数,要逐个逐方向更新更小值。
void view(bool k[][100]){cout<<"地图\n";cout<<" 列\t";for(int j=0;j<=c+1;j++)cout<<j<<"";cout<<endl;for(int i=0;i<=r+1;i++){cout<<i<<"行\t";for(int j=0;j<=c+1;j++)cout<<(k[i][j]?'X':' ')<<"";cout<<endl;}	
}
void view(int k[][100],int ans){cout<<"最少线段数"<<ans<<endl;cout<<" 列\t";for(int j=0;j<=c+1;j++)cout<<j<<"";cout<<endl;for(int i=0;i<=r+1;i++){cout<<i<<"行\t";for(int j=0;j<=c+1;j++)cout<<num[i][j]<<"";cout<<endl;}cout<<endl; 
}
void go(int x,int y,int f,int numx,int& ans){int x2,y2;for(int i=0;i<4;i++){x2=x+d[i][0],y2=y+d[i][1];if(x2<0||x2>r+1||y2<0||y2>c+1)continue;//不能越界 int cost=(i==f?numx:numx+1);if(cost>=ans)continue;//剪枝，超过最少线段数的线路不用考虑 if(x2==tx&&y2==ty){ans=min(ans,cost);//cout<<"OK"<<endl;view(num,ans);return;}if(k[x2][y2]||num[x2][y2])continue;//如果是牌不能穿越 num[x2][y2]=cost;//标记，并记住步数go(x2,y2,i,cost,ans); num[x2][y2]=0;//回溯 }
}
int main(){//freopen("data.cpp","r",stdin);int t1=1;while(cin>>c>>r&&(r||c)){//多组地图，全部是0才结束 cin.get();//消融行结束标记 memset(k,0,sizeof(k));//初始化整个地图,0是可以走 char cx;//地图字符 for(int i=1;i<=r;i++){for(int j=1;j<=c;j++){cx=cin.get();k[i][j]=(cx=='X'?1:0);//卡片不能走 }cin.get();//消融行结束标记}cout<<"Board #"<<t1++<<":\n";//输出组信息int t2=1,x,y,//出发行列 x2,y2;//到达行列 while(cin>>sy>>sx>>ty>>tx&&(sx||sy||tx||ty)){//多组数据，全部是0才结束 //cout<<"出发："<<sx<<","<<sy<<"\t"<<tx<<","<<ty<<endl;memset(num,0,sizeof(num));//各点初始化为最大值 int ans=0x3f3f3f;//0x3f=63,不够大，0x3f3f3f=4194303够了//view(k);go(sx,sy,-1,0,ans);cout<<"Pair "<<t2++<<": ";if(ans==0x3f3f3f)cout<<"impossible.\n";else cout<<ans<<" segments.\n"; }cout<<endl;//每组地图后有空行 } return 0;
}

宽搜代码

#include <bits/stdc++.h>
using namespace std;
struct point{int x,y,//出发行列 d,//方向 num;//线段数 
};
bool k[100][100];//标记是不是牌， 
int r,c,//地图行列 sx,sy,tx,ty, //始发和终点位置 d[4][2]={{0,-1},{-1,0},{0,1},{1,0}},//左上右下四个方向的行列变化 num[100][100][4];//每个点四个方向的最少线段数,要逐个逐方向更新更小值。
int main(){//freopen("data2.cpp","r",stdin);int t1=1;while(cin>>c>>r&&(r||c)){//多组地图，全部是0才结束 cin.get();//消融行结束标记 memset(k,0,sizeof(k));//初始化整个地图,0是可以走 char cx;//地图字符 for(int i=1;i<=r;i++){for(int j=1;j<=c;j++){cx=cin.get();if(cx=='X')k[i][j]=1;//k[i][j]=(cx=='X'?1:0);//卡片不能走 }cin.get();//消融行结束标记}cout<<"Board #"<<t1++<<":\n";//输出组信息int t2=1,x,y,//出发行列 x2,y2;//到达行列 while(cin>>sy>>sx>>ty>>tx&&(sx||sy||tx||ty)){//多组数据，全部是0才结束 memset(num,0x3f3f3f,sizeof(num));//各点初始化为最大值 queue<point> q;//宽搜队列 q.push(point{sx,sy,-1,0});//出发，下次方向都算不同，就会0+1多个线路for(int i=0;i<4;i++)num[sx][sy][i]=0;//出发位置各方向无线段 int ans=0x3f3f3f,//找最少线段数 cost;//中间值，存线段数变化结果 while(!q.empty()){point p=q.front();q.pop();x=p.x,y=p.y;for(int i=0;i<4;i++){//四个方向逐个尝试 x2=x+d[i][0],y2=y+d[i][1];if(x2<0||x2>r+1||y2<0||y2>c+1)continue;//出界 cost=(p.d==i?p.num:p.num+1);//方向一样线段数不变，否则多条线段 if(x2==tx&&y2==ty){//到达目标 if(num[x2][y2][i]>cost)num[x2][y2][i]=cost;ans=min(ans,cost);//更新最终最少线段数 }if(k[x2][y2])continue;//不能穿越牌if(num[x2][y2][i]>cost){//更少的线段数才更新并出发。 num[x2][y2][i]=cost;//更新该点i方向上的最少线段数 q.push(point{x2,y2,i,cost});//从新达点出发 }}}cout<<"Pair "<<t2++<<": ";if(ans==0x3f3f3f)cout<<"impossible.\n";else cout<<ans<<" segments.\n"; }cout<<endl;//每组地图后有空行 } return 0;
}

深搜数据

地图列     01234567
0行
1行       XXXX
2行         XX
3行      XX  X
4行      XXX  X
5行
Board #1:
出发：3,1       4,6
地图列     01234567
0行
1行       XXXX
2行         XX
3行      XX  X
4行      XXX  X
5行
OK
最少线段数10列     01234567
0行     23333333
1行     20000054
2行     20000067
3行     10000098
4行     00000000
5行     00000000OK
最少线段数9列     01234567
0行     23333333
1行     20000054
2行     20000067
3行     10000008
4行     00000008
5行     00000000OK
最少线段数6列     01234567
0行     23333333
1行     20000054
2行     20000060
3行     10000060
4行     00000000
5行     00000000OK
最少线段数5列     01234567
0行     23333333
1行     20000004
2行     20000004
3行     10000004
4行     00000004
5行     00000000OK
最少线段数4列     01234567
0行     23333330
1行     20000040
2行     20000040
3行     10000040
4行     00000000
5行     00000000OK
最少线段数3列     01234567
0行     01222220
1行     01000030
2行     01000030
3行     00000030
4行     00000000
5行     00000000Pair 1: 3 segments.

演示图

在这里插入图片描述

总结

1.问的不是步数，而是线段数
2.出发到到达方向一样，是一条线段，
不一样是两条线段
所以出发位置得带方向
3.宽搜，从不同方向到达该点，用更少线段数更新。不少不更新
例：短距离多线段，上2右1下1右1下1左2可达目标，是6线段
长距离少线段，上2右2下2左2，是4线段
4.数组得初始化。
如果用字符数组表示地图，外延得初始化，否则有可能是’X’，不能通过。
5.从大开始找最小，
初始化整型数组(各点最少线段数num[100][100][4])，可以用 memset(num,0X3f3f3f,sizeof(num))
十六进制0X3f=整数63，不够大.
十六进制0X3f3f3f=整数4194303.
再大就得逐一赋值。
6.深搜就是尝试所有的情况，关键就是剪

文章目录

题目

深搜代码

宽搜代码

深搜数据

演示图

总结

相关文章：