递归1——递归入门

目录

1.递归

2.递归的基本题目

2.1.题目一——P5739 【深基7.例7】计算阶乘 - 洛谷 | 计算机科学教育新生态

2.2.题目二——B2064 斐波那契数列 - 洛谷 | 计算机科学教育新生态 

2.3.题目三——B2142 求 1+2+3+...+N 的值 - 洛谷 | 计算机科学教育新生态

2.4.题目四——B2144 阿克曼（Ackermann）函数 - 洛谷 | 计算机科学教育新生态 

2.5.题目五——B2145 digit 函数 - 洛谷 | 计算机科学教育新生态 

2.6.题目六——B2147 求 f(x,n) - 洛谷 | 计算机科学教育新生态 

2.7.题目七——B2148 再求 f(x,n) - 洛谷 | 计算机科学教育新生态 

2.8.题目八——B2143 进制转换 - 洛谷 | 计算机科学教育新生态 

3.二叉树里面的递归

3.1.题目一——100. 相同的树 - 力扣（LeetCode）

3.2.题目二——101. 对称二叉树 - 力扣（LeetCode） 

3.3.题目三 ——572. 另一棵树的子树 - 力扣（LeetCode）

3.4.题目四——144. 二叉树的前序遍历 - 力扣（LeetCode）

3.5.题目五——94. 二叉树的中序遍历 - 力扣（LeetCode）

3.6.题目六——145. 二叉树的后序遍历 - 力扣（LeetCode） 

---

从这章，我们先讲递归，然后讲搜索，然后再讲回溯算法。

1.递归

1.1.递归的基本知识

• 什么是递归

我只讲3个东西来讲递归

1. 二叉树的遍历
2. 快排：先选一个基准元素，将数组分成3部分，然后让左边部分进行排序，再让右边部分排序
3. 归并：取数组中点，让数组分成两部分，然后先让左边部分先排序，再让右边部分排序，然后合并两个数组

---

•  为什么会用到递归？

本质就是这个问题可以拆分为多个相同的子问题，子问题又可以拆分成相同的子问题。

这个就像是数学的F(x,y)通用的。

---

• 如何理解递归？

1.画递归展开的细节图

2.二叉树的题目

3.宏观看待递归

• 不要在意递归的细节展开图
• 把递归的函数当成一个黑盒
• 相信这个黑盒一定能完成任务
• 此外，我们一定要设置递归结束的地方

我们只关心当前的这个任务能不能顺利完成，如果当前可以完全，那么递归一定也可以（注意要加一个结束条件），就像下面这样子

---

• 如何写好一个递归

1. 我们先找到一个相同的子问题  ->   这个决定了函数头的设计
2. 我们只关心某一个子问题是怎么解决的 ->这个决定函数体的书写
3. 注意一下递归函数的出口——>就是什么时候不能递归的时候，就让函数返回

1.2.递归和深度优先遍历（DFS)

其实我们发现这两货的执行逻辑是一模一样啊！！

1.3.递归和循环/迭代

 递归本质是完成重复的子任务，循环也是完成重复的子任务

• 递归算法

优点：代码简洁、清晰，并且容易验证正确性。（如果你真的理解了算法的话，否则你更晕）

缺点：它的运行需要较多次数的函数调用，如果调用层数比较深，需要增加额外的堆栈处理（还有可能出现堆栈溢出的情况），比如参数传递需要压栈等操作，会对执行效率有一定影响。但是，对于某些问题，如果不使用递归，那将是极端难看的代码。

• 循环算法：

优点：速度快，结构简单。

缺点：并不能解决所有的问题。有的问题适合使用递归而不是循环。如果使用循环并不困难的话，最好使用循环。

• 递归算法和循环算法总结：

1. 一般递归调用可以处理的算法，也通过循环去解决常需要额外的低效处理。

2. 现在的编译器在优化后，对于多次调用的函数处理会有非常好的效率优化，效率未必低于循环。

3.递归和循环两者完全可以互换。如果用到递归的地方可以很方便使用循环替换，而不影响程序的阅读，那么替换成递归往往是好的。（例如：求阶乘的递归实现与循环实现。）

2.递归的基本题目

2.1.题目一——P5739 【深基7.例7】计算阶乘 - 洛谷 | 计算机科学教育新生态

这题其实非常简单

#include<iostream>
using namespace std;int fact(int n)
{if(n==1)return 1;elsereturn fact(n-1)*n;
}int main()
{int a;cin>>a;cout<<fact(a)<<endl;
}

2.2.题目二——B2064 斐波那契数列 - 洛谷 | 计算机科学教育新生态 

这题还是很简单的

#include<iostream>
using namespace std;int res(int n)
{if(n==1||n==2)return 1;elsereturn res(n-1)+res(n-2);
}int main()
{int n;cin>>n;while(n--){int m;cin>>m;cout<<res(m)<<endl;}
}

2.3.题目三——B2142 求 1+2+3+...+N 的值 - 洛谷 | 计算机科学教育新生态

很简单的题目，不必多说 

#include<iostream>
using namespace std;int res(int n)
{if(n==1)return 1;elsereturn res(n-1)+n;
}int main()
{int m;cin>>m;cout<<res(m)<<endl;
}

 

2.4.题目四——B2144 阿克曼（Ackermann）函数 - 洛谷 | 计算机科学教育新生态 

这个理解题目很重要啊

#include<iostream>
using namespace std;int akm(int m,int n)
{if(m==0)return n+1;else if(m>0&&n==0)return akm(m-1,1);elsereturn akm(m-1,akm(m,n-1));
}int main()
{int m,n;cin>>m>>n;cout<<akm(m,n)<<endl;
}

 

2.5.题目五——B2145 digit 函数 - 洛谷 | 计算机科学教育新生态 

这里就上了一点难度了啊，怎么做呢？ 

我们知道

1. n/10就能减去n最右边那个数字
2. n%10就能获得最右边那个数字

而我们题目要的是右边第k个数字，说明我们最后的结果一定是n%10出来的。

所以终止条件就是当k==1的时候，直接返回n%10即可。

这样子我们就很容易写出下面这个代码

#include<iostream>
using namespace std;int digit(int n,int k)
{if(k==1)return n%10;elsereturn digit(n/10,k-1);
}int main()
{int n,k;cin>>n>>k;cout<<digit(n,k)<<endl;
}

2.6.题目六——B2147 求 f(x,n) - 洛谷 | 计算机科学教育新生态 

这个还是非常简单的

#include<iostream>
#include<cmath>
using namespace std;float f(float x,int n)
{if(n==1)return sqrt(1+x);elsereturn sqrt(n+f(x,n-1));
}int main()
{float x;int n;cin>>x>>n;printf("%.2f\n", f(x,n));
}

  

2.7.题目七——B2148 再求 f(x,n) - 洛谷 | 计算机科学教育新生态 

这个明眼人就看出来了！！

#include<bits/stdc++.h>
using namespace std;float f(float x,int n)
{if(n==1)return x/(1+x);elsereturn x/(n+f(x,n-1));
}int main()
{float x;int n;cin>>x>>n;printf("%.2f\n",f(x,n));
}

2.8.题目八——B2143 进制转换 - 洛谷 | 计算机科学教育新生态 

 

 这题上强度了啊！！！

首先我们得知道，这个题目的最大进制是16进制，所以我们必须得能表示16进制，那我们怎么快速的表示一个16进制的数字呢？

我们可以使用一个string，然后下标和这个数字一一对应。

其中2——16进制的所有表达方式都能在上面这个s里面找到。

接着，我们仔细看下面这个步骤

我们发现是不是好像有规律啊？

最后递归得到的就是最高位的数字，我们完全可以让它先出来。

看完之后，有没有通透一点，就是我们完全可以写出下面这个代码

 #include <iostream>using namespace std;string s = "0123456789ABCDEF";void x_to_m(int x, int m){if (x >= m)x_to_m(x / m, m);cout << s[x % m];}int main(){int x = 0;int m = 0;cin >> x >> m;x_to_m(x, m);return 0;}

 

3.二叉树里面的递归

理解递归，上面的那些题目可不够，必须来看一下二叉树的递归。

3.1.题目一——100. 相同的树 - 力扣（LeetCode）

 

判断两棵二叉树是否相同，也可以将其分解为子问题：

1. 比较两棵树的根是否相同。
2. 比较两根的左子树是否相同。
3. 比较两根的右子树是否相同。

代码：

class Solution {
public:// 判断两棵二叉树是否相同bool isSameTree(TreeNode* p, TreeNode* q) {if (p == NULL && q == NULL) // 两棵树均为空，则相同return true;if (p == NULL || q == NULL) // 两棵树中只有一棵树为空，则不相同return false;if (p->val != q->val) // 两棵树根的值不同，则不相同return false;return isSameTree(p->left, q->left) && isSameTree(p->right,q->right); // 两棵树的左子树相同并且右子树相同，则这两棵树相同}
};

 

3.2.题目二——101. 对称二叉树 - 力扣（LeetCode） 

 

 对称二叉树，这里所说的对称是指镜像对称：

要判断某二叉树是否是对称二叉树，则判断其根结点的左子树和右子树是否是镜像对称即可。

因为是镜像对称，所以左子树的遍历方式和右子树的遍历方式是不同的，准确来说，左子树和右子树的遍历是反方向进行的。

如下图：

图中红蓝轨迹同时进行，同时结束。

1. 若在遍历过程中发现镜像对称的某两个结点值不同，则无需继续遍历，此时已经可以判断该树不是对称二叉树
2. 只有当红蓝轨迹成功遍历完毕后，才能断定该树是对称二叉树。

我们很快就能写出代码

class Solution {
public:// 判断镜像位置是否相等bool travel(TreeNode* left, TreeNode* right) {if (left == NULL && right == NULL) // 红蓝轨迹同时遍历到NULL，函数返回return true;if (left == NULL ||right ==NULL) // 红蓝指针中，一个为NULL，另一个不为NULL，即镜像不相等return false;if (left->val != right->val) // 红蓝指针指向的结点值不同，即镜像不相等return false;// 子问题：左子树遍历顺序：先左后右，右子树遍历顺序：先右后左。若两次遍历均成功，则是对称二叉树return travel(left->left, right->right) &&travel(left->right, right->left);}bool isSymmetric(TreeNode* root) {if (root == NULL) // 空树是对称二叉树return true;return travel(root->left, root->right); // 判断镜像位置是否相等}
};

3.3.题目三 ——572. 另一棵树的子树 - 力扣（LeetCode）

 

 

思路：
依次判断以 root 中某一个结点为根的子树是否与subRoot相同。 

class Solution {
public:// 比较以root和subRoot为根结点的两棵树是否相等bool Compare(TreeNode* root, TreeNode* subRoot) {if (root == NULL && subRoot == NULL) // 均为空树，相等return true;if (root == NULL || subRoot == NULL) // 一个为空另一个不为空，不相等return false;if (root->val != subRoot->val) // 结点的值不同，不相等return false;// 比较两棵树的子结点return Compare(root->left, subRoot->left) &&Compare(root->right, subRoot->right);}// 另一个树的子树bool isSubtree(TreeNode* root, TreeNode* subRoot) {if (root == NULL) // 空树，不可能是与subRoot相同（subRoot非空）return false;if (Compare(root,subRoot)) // 以root和subRoot为根，开始比较两棵树是否相同return true;// 判断root的左孩子和右孩子中是否有某一棵子树与subRoot相同return isSubtree(root->left, subRoot) ||isSubtree(root->right, subRoot);}
};

3.4.题目四——144. 二叉树的前序遍历 - 力扣（LeetCode）

二叉树的前序遍历不知道是什么？自己去这里看看：链式二叉树的基本操作1-CSDN博客

class Solution {
public:// 前序遍历的递归函数// 参数ret用于存储遍历的结果，root是当前遍历到的节点void preorder(vector<int>& ret, TreeNode* root){// 如果当前节点为空，直接返回，不执行任何操作if(root == NULL)return;    // 将当前节点的值添加到结果集ret中ret.push_back(root->val);// 递归遍历左子树preorder(ret, root->left);// 递归遍历右子树preorder(ret, root->right);}vector<int> preorderTraversal(TreeNode* root) {// 创建一个向量ret，用于存储遍历的结果vector<int> ret; // 调用递归函数preorder进行前序遍历，并将结果存储在ret中preorder(ret, root);// 返回存储遍历结果的向量return ret;}
};

3.5.题目五——94. 二叉树的中序遍历 - 力扣（LeetCode）

 

这题非常简单啊，我不想过多赘述啊！

class Solution {
public:// 中序遍历的递归函数// 参数ret用于存储遍历的结果，root是当前遍历到的节点void inorder(vector<int>& ret, TreeNode* root){// 如果当前节点为空，直接返回，不执行任何操作if(root == NULL)return;    // 递归遍历左子树inorder(ret, root->left);// 将当前节点的值添加到结果集ret中// 此时，左子树的所有节点值都已经被添加到ret中了ret.push_back(root->val);// 递归遍历右子树// 此时，当前节点的值也已经被添加到ret中了inorder(ret, root->right);}vector<int> inorderTraversal(TreeNode* root) {// 创建一个向量ret，用于存储遍历的结果vector<int> ret; // 调用递归函数inorder进行中序遍历，并将结果存储在ret中inorder(ret, root);// 返回存储遍历结果的向量return ret;}
};

3.6.题目六——145. 二叉树的后序遍历 - 力扣（LeetCode） 

class Solution {
public:// 后序遍历的递归函数// 参数ret用于存储遍历的结果，root是当前遍历到的节点void postorder(vector<int>& ret, TreeNode* root){// 如果当前节点为空，直接返回，不执行任何操作if(root == NULL)return;        // 递归遍历左子树postorder(ret, root->left);    // 递归遍历右子树postorder(ret, root->right);// 将当前节点的值添加到结果集ret中// 此时，左子树和右子树的所有节点值都已经被添加到ret中了ret.push_back(root->val);}vector<int> postorderTraversal(TreeNode* root) {// 创建一个向量ret，用于存储遍历的结果vector<int> ret; // 调用递归函数postorder进行后序遍历，并将结果存储在ret中postorder(ret, root);// 返回存储遍历结果的向量return ret;}
};

4.递归必刷题 

4.1.题目一——面试题 08.06. 汉诺塔问题 - 力扣（LeetCode）

 

 

 我知道大家可能看不懂题目，我们看一个例子就好

这样子应该理解了吧。

但是我们这道题为什么可以使用递归来解决？

首先我们得明白，如何解决这个汉诺塔解决？

我们可以先从最简单的情况考虑：

假设n=1，只有⼀个盘⼦，很简单，直接把它从A中拿出来，移到C上；

---

 如果n=2呢？

我们最先要做的就是想法设法的将大盘子放到C上面去，这时候我们就要借助B了，因为⼩盘⼦必须时刻都在⼤盘⼦上⾯，共需要3步（为 了⽅便叙述，记A中的盘⼦从上到下为1号，2号）：

• a. 1号盘⼦放到B上；
• b. 2号盘⼦放到C上；
• c. 1号盘⼦放到C上。

⾄此，C中的盘⼦从上到下为1号，2号。

我们仔细观察就会发现

---

如果n=3呢？

我们还是先想办法将大盘子放到C上面去。

这是我们需要⽤到n=2时的策略，将A上⾯的两个盘⼦挪到B上，再将最⼤的盘 ⼦挪到C上，最后将B上的⼩盘⼦挪到C上就完成了所有步骤。

例如n=3时如下图： A B C 因为A中最后处理的是最⼤的盘⼦，所以在移动过程中不存在⼤盘⼦在⼩盘⼦上⾯的情况。

 

有没有发现这个过程里面

这样子能不能看出规律来啊！！重复子问题，我是已经看出来了！！

我们直接写代码就好。

class Solution 
{
public:void hanota(vector<int>& a, vector<int>& b, vector<int>& c) {// 调用深度优先搜索函数，参数包括三个柱子（a, b, c）和盘子数量（a.size()）dfs(a, b, c, a.size());}// 深度优先搜索函数，用于递归地解决汉诺塔问题void dfs(vector<int>& a, vector<int>& b, vector<int>& c, int n){// 基本情况：如果只有一个盘子，直接将其从柱子a移动到柱子cif(n == 1){c.push_back(a.back()); // 将柱子a的最后一个盘子移动到柱子ca.pop_back();          // 从柱子a移除这个盘子return;}// 递归步骤1：将n-1个盘子从柱子a通过柱子c移动到柱子bdfs(a, c, b, n - 1);// 当前步骤：将第n个盘子（最大的盘子）从柱子a移动到柱子cc.push_back(a.back()); // 将柱子a的最后一个盘子移动到柱子ca.pop_back();          // 从柱子a移除这个盘子// 递归步骤2：将n-1个盘子从柱子b通过柱子a移动到柱子cdfs(b, a, c, n - 1);}
};

4.2.题目二——21. 合并两个有序链表 - 力扣（LeetCode）

 

 

我们这道题目其实之前已经做过的，但是我们今天要使用递归的方式来解决这个问题。

我们使用递归就得找到重复出现的子问题。

我们发现，我们可以先对比两个链表的第一个结点，看看哪个结点小，就先把这个结点放进我们的新链表里面，然后接着重复上面的这个步骤。

接下来我们就要思考下面三个问题

重复子问题就是合并两个有序链表，函数头就是传进去一个链表指针，返回新的链表指针

我们的主要步骤就是比大小

• 如果第一个链表的第一个结点的值小于第二个链表的第一个结点的值，就让第一个链表的第一个结点当新链表的第一个结点，然后让第一个链表的第2个结点和第二个链表的第1个比较。
• 如果第一个链表的第一个结点的值大于等于第二个链表的第一个结点的值，就让第二个链表的第一个结点当新链表的第一个结点，然后让第二个链表的第2个结点和第一个链表的第1个比较。

递归的出口

• 就是一条链表为空的时候，返回另外一条链表。

class Solution 
{public:// 定义一个函数，用于合并两个已排序的链表ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {// 如果第一个链表为空，则直接返回第二个链表if(l1 == nullptr) return l2;// 如果第二个链表为空，则直接返回第一个链表if(l2 == nullptr) return l1;// 比较两个链表当前节点的值// 如果第一个链表的当前节点值小于或等于第二个链表的当前节点值if(l1->val <= l2->val){// 递归调用mergeTwoLists函数，传入第一个链表的下一个节点和第二个链表// 将返回的结果设置为第一个链表的当前节点的下一个节点l1->next = mergeTwoLists(l1->next, l2);// 返回第一个链表的当前节点作为合并后链表的头节点（因为l1的值较小或相等）return l1;}else{// 否则，如果第二个链表的当前节点值小于第一个链表的当前节点值// 递归调用mergeTwoLists函数，传入第一个链表和第二个链表的下一个节点// 将返回的结果设置为第二个链表的当前节点的下一个节点l2->next = mergeTwoLists(l1, l2->next);// 返回第二个链表的当前节点作为合并后链表的头节点（因为l2的值较小）return l2;}}
};

 

其实，我们只需要看递归的某一步骤——比较两个结点的值

我们的目的是返回一个头指针（因为题目需要头指针）。

所以这个递归就是找谁是头指针的问题！！！。

所以我们可以仔细看看，假设两个链表各剩下一个结点了，这个时候我们只需要判断这两个结点是否存在，如果其中一个不存在，就返回另外一个来当头结点，

如果都存在，则进行比较它们的值，谁小就先让它当后面序列的头指针，然后返回这个结点即可。

这样子想有没有更容易理解一点。

4.3.题目三—— 206. 反转链表 - 力扣（LeetCode）

 

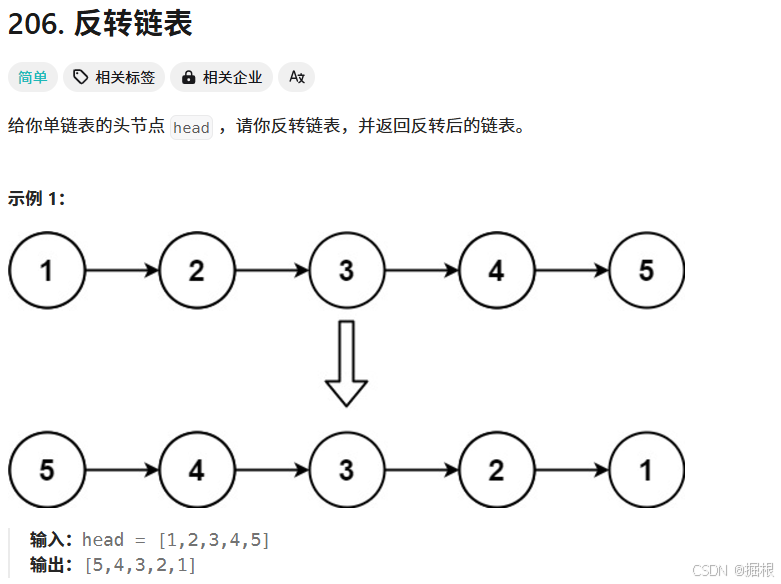
 这里从两个视角来看待这个问题

• 宏观视角来完成（我们直接看递归的最后一步）

就是我先让当前结点的下面一个结点先进行逆置，这样子一直递归，就会是下面这个情况

这个时候我们只需要像下面这样子做即可

总结起来就两步

• 先让当前结点的后面的链表先逆置，并且把新的头结点返回
• 让当前结点添加到逆置后的链表后面

什么时候不需要逆置了？

• 链表为空或者只有1个结点

class Solution 
{public:ListNode* reverseList(ListNode* head) {// 如果链表为空（head为nullptr）或者只有一个节点（head->next为nullptr），则直接返回headif(head == nullptr || head->next == nullptr) return head;// 递归调用reverseList函数，传入head的下一个节点，目的是反转head之后的链表// newHead此时是反转后链表的头节点ListNode* newHead = reverseList(head->next);// 将当前节点的下一个节点的next指针指向当前节点，实现局部反转// 这一步是在递归返回的过程中执行的，确保了每次递归返回时，当前节点都被正确地插入到反转后的链表尾部之后head->next->next = head;// 将当前节点的next指针置为nullptr，断开当前节点与原来链表的连接// 这一步是必须的，否则会出现环或者多个节点指向原链表的后续节点head->next = nullptr;// 返回新的头节点return newHead;}
};

4.4.题目四——24. 两两交换链表中的节点 - 力扣（LeetCode）

 

这题我们怎么思考呢？

我们还是直接看最后一步，

就是假设链表后面所有结点都已经交换好了，交换好后都返回新的头结点。

就剩现在两个结点需要交换了，这个时候，这个时候我们只需要将第二个结点的next指针指向第一个结点，第一个结点的next指针指向新的头结点，然后我们再更新一下头结点。

我们很容易就写出下面这个代码

class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head==nullptr||head->next==nullptr)return head;ListNode*newhead=swapPairs(head->next->next);ListNode*right=head->next;head->next->next=head;head->next=newhead;newhead=right;return newhead;}
};

4.5.题目五——50. Pow(x, n) - 力扣（LeetCode） 

 

我们很快就能写出下面这个

class Solution {
public:double myPow(double x, int n) {if(n==1)return x;elsereturn x*myPow(x,n-1);}
};

 但是它说我栈溢出了！！！

我们就可以先求n