当前位置：首页 > news >正文

Leecode Hot50

news 来源：原创 2025/7/13 18:47:54

文章目录

矩阵
- Solution73. 矩阵置零
- Solution54. 螺旋矩阵
- Solution48. 旋转图像
- Solution240. 搜索二维矩阵 II
二叉树
- 二叉树的四种遍历结果
- Solution94. 二叉树的中序遍历
- Solution104. 二叉树的最大深度
- Solution226. 翻转二叉树
- Solution101. 对称二叉树
- Solution543. 二叉树的直径
- Solution102. 二叉树的层序遍历
- Solution108. 将有序数组转换为二叉搜索树
- Solution98. 验证二叉搜索树
- Solution230. 二叉搜索树中第 K 小的元素
- Solution199. 二叉树的右视图
- Solution114. 二叉树展开为链表
- Solution105. 从前序与中序遍历序列构造二叉树
- Solution437. 路径总和 III
- Solution236. 二叉树的最近公共祖先

矩阵

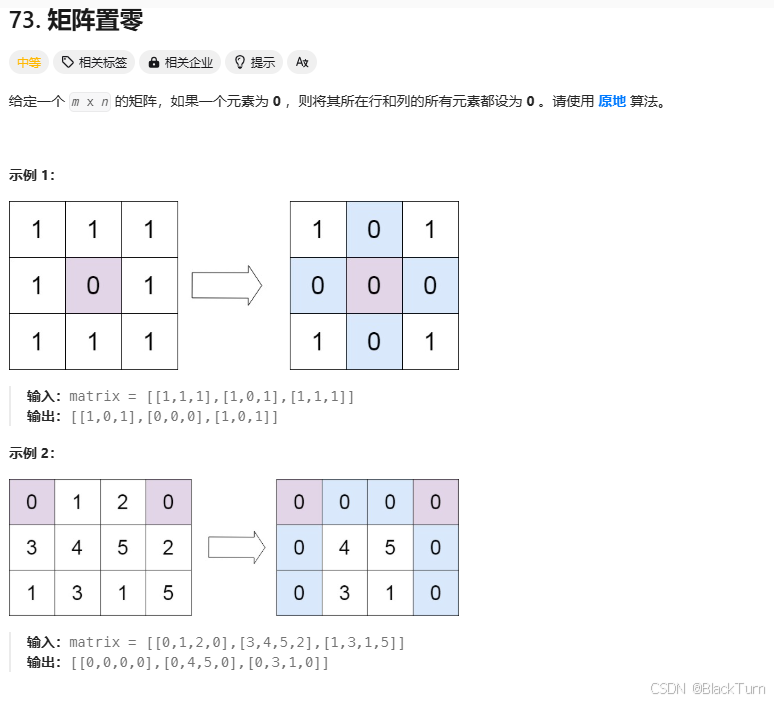
Solution73. 矩阵置零

代码思路说明：假如矩阵是{1, 2, 3},{4, 0, 6},{7, 8, 9}第一次遍历矩阵，得到两个数组：zeroRows = [false, true, false]，这个zeroRows记录需要置零的行，第二行需要置零zeroCols = [false, true, false]，这个zeroCols记录需要置零的列，第二列需要置零第二次遍历矩阵，如果某个元素所在的行或列被标记为需要置零，则将该元素置为零；如元素4所在的行被标记为需要置零，则将该元素置为零

public class Solution {public static void setZeroes(int[][] matrix) {int m = matrix.length; // 矩阵的行数int n = matrix[0].length; // 矩阵的列数// 第一遍遍历，记录需要置零的行和列boolean[] zeroRows = new boolean[m]; // 记录需要置零的行boolean[] zeroCols = new boolean[n]; // 记录需要置零的列for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == 0) {zeroRows[i] = true;zeroCols[j] = true;}}}// 第二遍遍历，根据记录的结果将对应行和列置为零for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (zeroRows[i] || zeroCols[j]) {matrix[i][j] = 0;}}}}// 测试函数public static void main(String[] args) {int[][] matrix = {{1, 2, 3},{4, 0, 6},{7, 8, 9}};System.out.println("原始矩阵:");printMatrix(matrix);setZeroes(matrix);System.out.println("处理后的矩阵:");printMatrix(matrix);}/*** 打印矩阵** @param matrix 待打印的矩阵*/public static void printMatrix(int[][] matrix) {for (int[] row : matrix) {for (int num : row) {System.out.print(num + " ");}System.out.println();}}
}

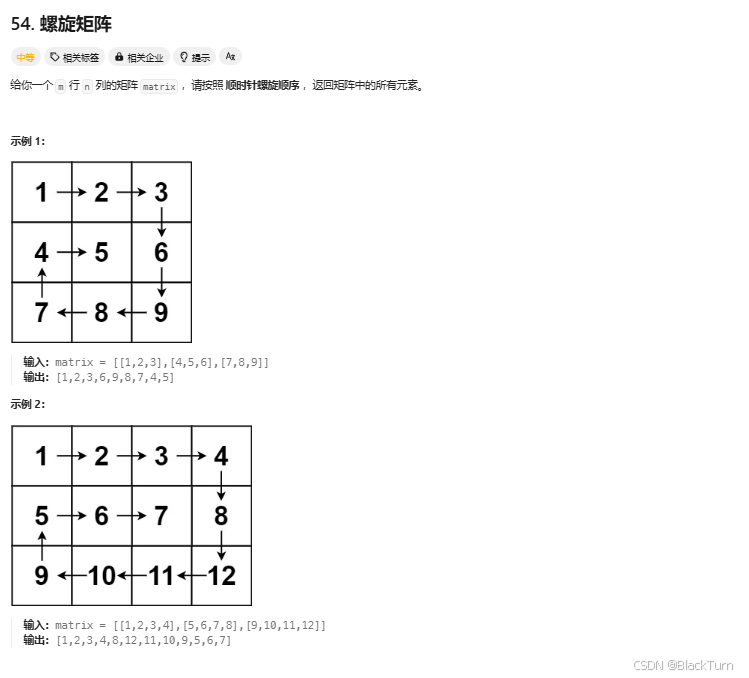
Solution54. 螺旋矩阵

 矩阵是：{1, 2, 3},{4, 5, 6},{7, 8, 9}①从左到右遍历，遍历了1->3  用matrix[top][i]其中top是0，而i是0,1,2②从从上到下遍历，遍历了6->9  用matrix[i][right]其中right是2，而i是1,2③从右到左遍历，遍历了8->7  用matrix[bottom][i]其中bottom是2，而i是1,0④从下到上遍历左边,遍历了7->4  用matrix[i][left]其中left是0，而i是2,1⑤从左到右遍历，遍历了4->5  用matrix[top][i]其中top是1，而i是0,1

public class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return result; // 如果矩阵为空，则直接返回空列表}int rows = matrix.length;int cols = matrix[0].length;int left = 0, right = cols - 1;int top = 0, bottom = rows - 1;while (left <= right && top <= bottom) {// 从左到右遍历上边，遍历了1->3和最后的4->5for (int i = left; i <= right; i++) {result.add(matrix[top][i]);}top++;// 从上到下遍历右边，遍历了6->9for (int i = top; i <= bottom; i++) {result.add(matrix[i][right]);}right--;// 如果还有行需要遍历（注意此时top已经加1，所以要判断top-1是否小于等于bottom）if (top <= bottom) {// 从右到左遍历下边,遍历了8->7for (int i = right; i >= left; i--) {result.add(matrix[bottom][i]);}bottom--;}// 如果还有列需要遍历（注意此时right已经减1，所以要判断left是否小于等于right）if (left <= right) {// 从下到上遍历左边,遍历了7->4for (int i = bottom; i >= top; i--) {result.add(matrix[i][left]);}left++;}}return result;}// 主函数，用于测试public static void main(String[] args) {Solution spiralMatrix = new Solution();int[][] matrix = {{1, 2, 3},{4, 5, 6},{7, 8, 9}};List<Integer> result = spiralMatrix.spiralOrder(matrix);// 打印结果for (int num : result) {System.out.print(num + " ");}}
}

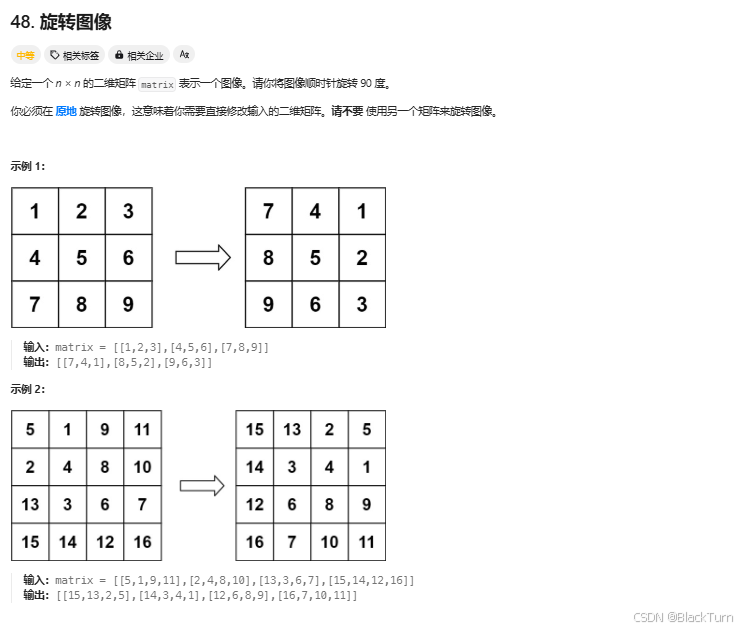
Solution48. 旋转图像

第一步：转置矩阵将矩阵的行变成列，列变成行。在代码中，通过遍历矩阵的上三角（包括对角线），并交换 matrix[i][j] 和 matrix[j][i] 来实现转置。1, 2             1, 33, 4   转置后变成  2, 4第二步：反转每一行遍历每一行，每一行数据都进行反转1, 3                  3, 12, 4   每一行反转后变成  4, 2如此变完成了旋转90度

public class Solution {// 主方法，用于测试public static void main(String[] args) {int[][] matrix = {{1, 2, 3},{4, 5, 6},{7, 8, 9}};rotate(matrix);// 打印旋转后的矩阵for (int[] row : matrix) {for (int num : row) {System.out.print(num + " ");}System.out.println();}}/*** 将二维矩阵原地顺时针旋转90度* @param matrix n × n 的二维矩阵*/public static void rotate(int[][] matrix) {int n = matrix.length;// 第一步：转置矩阵for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// 第二步：反转每一行for (int i = 0; i < n; i++) {int left = 0, right = n - 1;while (left < right) {// 交换matrix[i][left]和matrix[i][right]int temp = matrix[i][left];matrix[i][left] = matrix[i][right];matrix[i][right] = temp;left++;right--;}}}
}

Solution240. 搜索二维矩阵 II

从矩阵的右上角或左下角开始搜索：从右上角开始搜索时，如果当前元素大于目标值，我们可以向左移动一列（因为左边的元素更小）；如果当前元素小于目标值，我们可以向下移动一行（因为下边的元素更大）。这样，我们总是朝着可能包含目标值的方向移动，直到找到目标值或搜索到矩阵的边界为止。

public class Solution {// 主方法，用于测试public static void main(String[] args) {int[][] matrix = {{1, 4, 7, 11, 15},{2, 5, 8, 12, 19},{3, 6, 9, 16, 22},{10, 13, 14, 17, 24},{18, 21, 23, 26, 30}};int target = 5;boolean result = searchMatrix(matrix, target);System.out.println("目标值是否存在: " + result);}public static boolean searchMatrix(int[][] matrix, int target) {if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return false;}int m = matrix.length; // 矩阵的行数int n = matrix[0].length; // 矩阵的列数int row = 0; // 从第一行开始int col = n - 1; // 从最后一列开始while (row

Leecode Hot50

文章目录矩阵Solution73. 矩阵置零Solution54. 螺旋矩阵Solution48. 旋转图像Solution240. 搜索二维矩阵 II二叉树二叉树的四种遍历结果Solution94. 二叉树的中序遍历Solution104. 二叉树的最大深度Solution226. 翻转二叉树Solution101. 对称二叉树Solution543. 二叉树的直径S…...

编程日记 2025/7/13 18:47:54

解决 Gradle 构建错误：Could not get unknown property ‘withoutJclOverSlf4J’

解决 Gradle 构建错误：Could not get unknown property ‘withoutJclOverSlf4J’ 在构建 Spring 源码或其他基于 Gradle 的项目时，可能会遇到如下错误： Could not get unknown property withoutJclOverSlf4J for object of type org.gradle…...

编程日记 2025/7/12 13:37:14

C++ 初阶总复习（16~30）

C 初阶总复习 （16~30） 目的16. 2009. volatile关键字的作用17. 2010.什么是多态简单介绍下C的多态18. 2011. 什么是虚函数介绍下C中虚函数的原理19. 2012 构造函数可以是虚函数嘛20. 2013.析构函数一定要是虚函数嘛？21. 2015. 什么是C中的虚…...

编程日记 2025/7/11 1:15:32

TDengine 中的异常恢复

简介本章主要介绍在 TDengine 执行命令过程中发生异常，如何手工终于执行的任务。可以终止连接，线上查询及终止事务。如果一个事务在一个复杂的应用场景中，连接和查询任务等有可能进入一种错误状态或者耗时过长迟迟无法结束，…...

编程日记 2025/7/12 12:04:20

二层框架组合实验

实验要求： 1,内网IP地址使用172.16.0.0/16分配 2,SW1和sw2之间互为备份 3,VRRP/STP/VLAN/Eth-trunk均使用 4,所有PC均通过DHCP获取IP地址 5,ISP只能配置IP地址 6,所有电脑可以正常访问ISP路由器环回实验思路顺序： 创建vlan eth-trunk 划分v…...

编程日记 2025/7/13 1:30:05

1.配置eth-trunk进行绑定 [LSW1]interface Eth-Trunk 0 [LSW1-Eth-Trunk0]q [LSW1]interface g0/0/2 [LSW1-GigabitEthernet0/0/2]eth-trunk 0 [LSW1-GigabitEthernet0/0/2]int g0/0/3 [LSW1-GigabitEthernet0/0/3]eth-trunk 0 [LSW1-GigabitEthernet0/0/3]display et…...

编程日记 2025/7/11 12:23:05

2025年信息系统与未来教育国际学术会议（ISFE 2025）

基本信息官网：www.icedcs.net 时间：2025年4月18-20日地点：中国-深圳简介 2025年信息系统与未来教育国际学术会议（ISFE 2025）作为第二届粤港澳大湾区教育数字化与计算机科学国际学术会议（EDCS 2025&…...

编程日记 2025/7/11 15:47:43

nacos 外置mysql数据库操作（docker 环境）

目录一、外置mysql数据库原因： 二、数据库准备工作三、构建nacos容器四、效果展示一、外置mysql数据库原因： 想知道nacos如何外置mysql数据库之前，我们首先要知道为什么要外置mysql数据库，或者说这样做有什么优点和好处&am…...

编程日记 2025/7/8 1:15:30

Windows 10 ARM64平台MFC串口程序开发

Windows 10 IoT ARM64平台除了支持新的UWP框架，也兼容支持老框架MFC。使得用户在Windows 10 IoT下可以对原MFC工程进行功能升级，不用在新框架下重写整个工程。熟悉MFC开发的工程师也可以在Windows 10 IoT平台下继续使用MFC进行开发。本文展示MFC串口程序…...

编程日记 2025/7/2 4:00:11

怎么使用pm2启动和暂停后端程序（后端架构nodejs+koa）

首先查看自己的pm2进程 pm2 list 或者 pm2 status 如果什么进程都没有，但是你确实有后端程序运行在服务器上，使用以下查看pm2程序的启动用户 ps aux | grep pm2就可以看到具体的用户和进行的信息接着转换到你要操作的pm2的进程用户下 sudo su - …...

编程日记 2025/7/4 18:42:19

AI人工智能-Jupyter NotbookPycharm：Py开发

安装命令： pip install jupyter 启动命令： jupyter notebook 启动成功后，下面网址会默认自动打开当前用户的根目录。其实这个页面显示的内容，是我们电脑目录C:\Users\当前用户\下的文件夹我们平常做实验，希望在…...

编程日记 2025/7/11 16:52:41

uniapp-小程序地图展示

一、当前页面直接获取 <view class"map"><map id"myMap" style"width: 100%; height: 40vh;" :latitude"latitude":longitude"longitude" :markers"markers" :scale"scale" :show-location&qu…...

编程日记 2025/7/9 1:31:43

使用 Python 进行链上数据监控：让区块链数据触手可及

使用 Python 进行链上数据监控：让区块链数据触手可及区块链技术正以前所未有的速度改变着各行各业，特别是在金融、供应链、物联网和智能合约等领域的应用，已经成为了一种新常态。然而，随着区块链网络的快速扩展和去中心化特性的不断强化，数据的可视化与监控变得愈发重要…...

编程日记 2025/7/13 18:45:28

CentOS 7 磁盘及分区管理笔记

一、查看磁盘信息 1. lsblk 命令作用：列出系统中所有的块设备（包括磁盘、分区等）及其相关信息，如设备名称、大小、类型等。命令格式：lsblk 示例： lsblk NAME MAJ:MIN RM SIZE RO TYPE MOUNTPOINT sd…...

编程日记 2025/7/12 18:51:58

python基础学习二（列表及字典的使用）

文章目录列表列表的创建获取列表中的多个元素判断列表中元素是否存在列表元素的添加操作列表元素的删除操作列表元素的修改列表的排序列表生成式字典字典的创建字典的常规操作字典的常用操作字典的视图操作字典元素的遍历字典的特点字典的生成式列表一个对象由id&#xff0…...

编程日记 2025/7/13 12:59:35

【NLP 50、损失函数 KL散度】

目录一、定义与公式 1.核心定义 2.数学公式 3.KL散度与交叉熵的关系二、使用场景 1.生成模型与变分推断 2.知识蒸馏 3.模型评估与优化 4.信息论与编码优化三、原理与特性 1.信息论视角 2.优化目标 3.局限性四、代码示例代码运行流程核心代码解析抵达梦想靠的不是狂热…...

编程日记 2025/7/11 5:54:13

macOS Jdk1.8安装(目前主流版本的jdk)

Jdk1.8安装 1、jdk安装包下载链接2、下载安装包（根据自己是什么系统进行下载）3、下载完成之后双击安装包进行安装安装好之后查看查看安装的版本需要查看JDK的安装路径(一般在/Library/Java/JavaVirtualMachines)配置环境变量1、jdk安装包下载链接 jdk8下载链接 https://www.…...

编程日记 2025/6/28 3:21:37

树莓派5智能家居中控：HomeAssistant全配置指南

一、硬件选型与系统架构 1.1 树莓派5的硬件优势 2023年发布的树莓派5采用Broadcom BCM2712处理器（4核Cortex-A76架构），相比前代产品具有三大突破性改进： 接口升级：首次支持PCIe 2.0接口，可扩展万兆网卡或…...

编程日记 2025/7/12 8:05:47

Dubbo（22）如何配置Dubbo的服务提供者？

配置Dubbo的服务提供者是实现分布式服务架构的重要步骤。服务提供者负责将服务注册到注册中心，使得服务消费者可以发现并调用这些服务。下面以一个完整的Spring Boot项目为例，详细介绍如何配置Dubbo的服务提供者。配置步骤引入依赖：在项目…...

编程日记 2025/7/10 9:47:18

【通道注意力机制】【SENet】Squeeze-and-Excitation Networks

0.论文摘要卷积神经网络建立在卷积操作的基础上，通过融合局部感受野内的空间和通道信息来提取有意义的特征。为了增强网络的表示能力，最近的一些方法展示了增强空间编码的好处。在本研究中，我们专注于通道关系，并提出了一种新颖…...

编程日记 2025/7/11 22:12:43

【SPP】蓝牙串口协议（SPP）深度解析：从 RS232 仿真到设备互联的技术实现

目录一、SPP协议概述 1.1 SPP的定位与核心功能 1.2 协议栈层次（SPP 协议模型） 1.3 技术原理 1.4 用户需求二、设备角色与连接模型 2.1 角色定义（DevA 与 DevB 交互） 2.2 角色动态切换 2.3 协议依赖关系三、数据传输：从 RS232 到蓝牙的映射 3.1 控制信号仿真…...

编程日记 2025/7/9 20:44:29

5.Excel：从网上获取数据

一用 Excel 数据选项卡获取数据的方法连接。二要求获取实时数据每1分钟自动更新数据。 A股市场_同花顺行情中心_同花顺财经网用上面方法将数据加载进工作表中。在表格内任意区域右键，刷新。自动刷新： 三缺点 Excel 只能爬取网页上表格类型的…...

编程日记 2025/7/10 1:22:47

基于RFID技术建筑物资材料智能管理解决方案

建筑行业仓库和物资材料管理面临诸多挑战，如工程设备重复利用的管理需求、物资出入库管理不规范、账物不符、物资丢失等问题。特别是在复杂多变的工地环境中，对物资进行科学规范的管理难度极大。上海岳冉基于RFID技术的建筑物资材料智能管理解决方案聚焦…...

编程日记 2025/7/9 1:14:05

详解CountDownLatch底层源码

大家好，我是此林。今天来分享一下CountDownLatch的底层源码。 CountDownLatch 是 Java 并发包 (java.util.concurrent) 中的线程之间同步工具类，主要用于协调多个线程的执行顺序。其核心思想是通过计数器实现线程间的"等待-唤醒"机制&#…...

编程日记 2025/7/13 14:48:38

Python每日一题(9)

Python每日一题 2025.3.29 一、题目二、分析三、源代码四、deepseek答案五、源代码与ai分析一、题目 question["""企业发放的奖金根据利润提成。利润(I)低于或等于10万元时,奖金可提10%,利润高于10万元,低于20万元时,低于10万元的部分按10%提成,高于10万元的部…...

编程日记 2025/7/3 1:11:53

一阶谓词逻辑表示法、产生式表示法、框架表示法深度对比

前文我们已经深度学习了一阶谓词逻辑表示法、产生式表示法和框架表示法这三种知识表示方法，那么它们之间有什么异同点呢？接下来我们对它们进行深度对比。首先，我得回忆这三种知识表示方法的基本概念和特点。（1）一阶谓词逻辑（FOPL）是基于形式逻辑的，使用谓词、变量、量…...

编程日记 2025/7/11 7:24:15

Tomcat生产服务器性能优化

试想以下这个情景：你已经开发好了一个程序，这个程序的排版很不错，而且有着最前沿的功能和其他一些让你这程序增添不少色彩的元素。可惜的是，程序的性能不怎么地。你也十分清楚，若现在把这款产品退出市场，肯…...

编程日记 2025/7/9 21:34:19

【算法day25】最长有效括号——给你一个只包含 ‘(‘ 和 ‘)‘ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

32. 最长有效括号给你一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。 https://leetcode.cn/problems/longest-valid-parentheses/ 2.方法二：栈 class Solution { public:int longestValid…...

编程日记 2025/7/10 18:34:39

Python之变量与数据类型总结

前言一、基本数据类型 1、整数（int） 2、浮点数（float） 3、布尔值（bool） 4、字符串（str） 二、复合数据类型 1、列表（list） 1.1、列表基础 1.1.1、列…...

编程日记 2025/7/12 15:58:13

【大模型基础_毛玉仁】5.3 附加参数法：T-Patcher

目录 5.3 附加参数法：T-Patcher5.3.1 补丁的位置1）键值存储体2）补丁设计 5.3.2 补丁的形式5.3.3 补丁的实现1）准确性2）局部性 5.3 附加参数法：T-Patcher 附加参数法：通过引入可训练的额外参数实…...

编程日记 2025/6/27 21:04:29

【19期获取股票数据API接口】如何用Python、Java等五种主流语言实例演示获取股票行情api接口之沪深A股实时交易数据及接口API说明文档

在量化分析领域，实时且准确的数据接口是成功的基石。经过多次实际测试，我将已确认可用的数据接口分享给正在从事量化分析的朋友们，希望能够对你们的研究和工作有所帮助，接下来我会用Python、JavaScript（Node.js&…...

编程日记 2025/7/10 21:30:04

RSA 简介及 C# 和 js 实现【加密知多少系列_4】

〇、简介谈及 RSA 加密算法，我们就需要先了解下这两个专业名词，对称加密和非对称加密。对称加密：在同一密钥的加持下，发送方将未加密的原文，通过算法加密成密文；相对的接收方通过算法将密文解密出来原文…...

编程日记 2025/6/28 1:34:08

Koordinator-Metric查询

以CollectAllPodMetricsLast()举例，看看koordinator怎样使用tsdb进行查询。 CollectAllPodMetricsLast() GenerateQueryParamsLast()传入metric采集间隔2倍时间调用CollectAllPodMetrics()func CollectAllPodMetricsLast(statesInformer statesinformer.StatesInformer, metr…...

编程日记 2025/7/13 10:33:29

LeetCode1两数之和

**思路：**懒得写了，如代码所示 /*** Note: The returned array must be malloced, assume caller calls free().*/ struct hashTable {int key;//存值int val;//存索引UT_hash_handle hh; }; int* twoSum(int* nums, int numsSize, int target, int* re…...

编程日记 2025/7/11 7:39:32

AOA与TOA混合定位，MATLAB例程，三维空间下的运动轨迹，滤波使用EKF，附下载链接

本文介绍一个MATLAB代码，实现基于到达角（AOA） 和到达时间（TOA） 的混合定位算法，结合扩展卡尔曼滤波（EKF） 对三维运动目标的轨迹进行滤波优化。代码通过模拟动态目标与基站网络&am…...

编程日记 2025/7/10 14:26:20

Java算法模板

合并区间统计不同区间的元素个数 //合并区间List<Integer> result new ArrayList<>();int start intervals.get(0)[0];int end intervals.get(0)[1];for(int i1;i<intervals.size();i){int[] curr intervals.get(i);if(curr[0]>end){//不能合并&…...

编程日记 2025/7/10 1:36:27

软件架构设计中的软件过程模型初识

软件架构设计中的软件过程模型是指导软件开发过程的框架，它们定义了软件开发的不同阶段、活动、任务和角色。结合具体的使用场景，可以更好地理解这些模型如何在实际项目中应用。以下将详细介绍几种常见的软件过程模型，并结合典型场景进行讲解…...

编程日记 2025/7/8 4:05:29

征程 6E mipi tx 系列之方案介绍

MIPI TX 到车机显示系统设计指南 IDE 介绍征程 6 IDE 架构图 IDE（Image Display Engine）包含图像显示单元（Image Display Unit）、图像数据输出模块（MIPI CSI2 Device 和 MIPI DSI）。通过 IDU 从内存中读…...

编程日记 2025/7/10 16:17:56

std::reference_wrapper 和 std::function的详细介绍

关于 std::reference_wrapper 和 std::function 的详细介绍及具体测试用例： 1. std::reference_wrapper（引用包装器） 核心功能包装引用：将引用转换为可拷贝、可赋值的对象支持隐式转换：可自动转换为原始引用类型容器…...

编程日记 2025/7/13 11:04:18

【day4】数据结构刷题树

6-1 二叉树的遍历函数接口定义： void InorderTraversal( BinTree BT ); void PreorderTraversal( BinTree BT ); void PostorderTraversal( BinTree BT ); void LevelorderTraversal( BinTree BT ); 其中BinTree结构定义如下： typedef struct TNode *Po…...

编程日记 2025/7/10 19:23:51

基于Selenium的IEEE Xplore论文数据爬取实战指南

基于Selenium的IEEE Xplore论文数据爬取实战指南一、项目背景与目标 IEEE Xplore作为全球知名的学术资源平台，收录了大量高质量科技文献。本教程将演示如何通过Python的Selenium库实现：自动化获取指定领域论文列表（以"构音障碍"为例）完整提取论文标题、摘要、…...

编程日记 2025/7/6 2:02:14

Vue2 项目将网页内容转换为图片并保存到本地

🌟 前言欢迎来到我的技术小宇宙！🌌 这里不仅是我记录技术点滴的后花园，也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛，这里总有一些内容能触动你的好奇心。🔍 &#x…...

编程日记 2025/7/12 10:51:13

flutter 专题七十一 Flutter 自定义单选控件

在Flutter 应用开发中，经常会遇到各种单选效果，虽然官方提供了Radio组件，但是并不能满足我们实际的开发需求，所以往往还需要自定义控件才能满足平时的开发需求。下面就平时开发中用到的单选进行介绍： 自定义SegmentBa…...

编程日记 2025/7/8 1:15:43

质因数个数--欧拉函数中统计纯素数

和互质数不同，这里统计的是纯素数部分就是x/i那一部分 #include<bits/stdc.h> using namespace std; #define N 100011 typedef long long ll; typedef pair<ll,int> PII; int n,m,k; ll eular(ll x) { ll an0;ll px;for(ll i2;i*i<x;i){if(x%i…...

编程日记 2025/7/2 17:51:05

RAG基建之PDF解析的“无OCR”魔法之旅

PDF文件转换成其他格式常常是个大难题，大量的信息被锁在PDF里，AI应用无法直接访问。如果能把PDF文件或其对应的图像转换成结构化或半结构化的机器可读格式，那就能大大缓解这个问题，同时也能显著增强人工智能应用的知识库。嘿，各位AI探险家们！今天我们将踏上了一段奇妙的…...

编程日记 2025/7/11 1:14:20

Web开发：数据的加密和解密

一、常见通用术语解析加盐：在密码中加入随机数据，提高安全性。摘要：固定长度的输出，用于数据完整性验证。加密：将数据转换为不可读形式，确保安全。撞库：通过暴力破解比对常见密码的攻击方式。…...

编程日记 2025/7/8 3:50:27

从零开始研发GPS接收机连载——15、使用新射频成功打卡日本地标

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档从零开始研发GPS接收机连载——15、使用新射频成功打卡日本地标前言MAX2771配置测试MAX2771完整程序测试前言话说笔者花了一笔巨资买了一个指甲盖般大小的MAX2771射频板&…...

编程日记 2025/6/30 20:25:45

linux压缩指令

今天我们来了解一下linux压缩指令,压缩是我们文件传输的一种重要手段,对此,我们是必须学习压缩指令的,那么话不多说,来看. 1.grep过滤查找，管道符，“｜”，表示将前一个命令的处理结果输出传递给后面的命令处理。基本语法&#x…...

编程日记 2025/7/7 6:49:41

智能提示词生成器：助力测试工程师快速设计高质量测试用例

在软件测试中，测试用例设计方法的选择和实施是确保软件质量的重要步骤。测试工程师经常需要根据不同的测试场景、参数维度和业务需求，设计出覆盖率高且有效的测试用例。然而，设计测试用例并非易事，特别是在面对复杂的业务逻辑时。为了帮助测试工程师高效生成测试用例提示…...

编程日记 2025/7/11 23:30:31

QML中使用Image显示图片和使用QQuickItem显示图片

在QML中显示图片时，Image元素和自定义QQuickItem有不同的特性和适用场景。以下是两者的详细对比及性能分析： 1. Image 元素优点： 声明式语法：简单直观，适合静态图片或简单动态需求 Image {source: "image.png&…...

编程日记 2025/7/1 8:24:11

文章目录

矩阵

Solution73. 矩阵置零

Solution54. 螺旋矩阵

Solution48. 旋转图像

Solution240. 搜索二维矩阵 II

相关文章：