数据结构——Map和Set
1. 搜索树
1. 概念
2. 查找

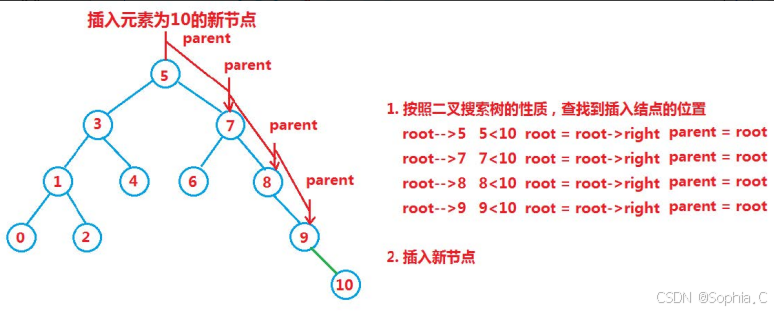
3. 插入
插入步骤
1. 如果树为空,则新节点成为根节点。
2. 如果树不为空
-
从根节点开始,比较插入值与当前节点的值。
-
根据比较结果,决定向左子树或右子树移动。
-
重复上述过程,直到找到一个空位置(即当前节点的左子节点或右子节点为空)。
-
将新节点插入到该空位置。
4. 删除
-
找到右子树的最小节点(或左子树的最大节点)。
-
用最小节点的值替换被删除节点的值。
-
删除右子树的最小节点。
public class BinarySearchTree {
//创建内部类,作为节点static class Node{public int val;public Node left;public Node right;//构造方法,初始化节点public Node(int val){this.val = val;}}public Node root;//查找public boolean search(int data){if(root==null){return false;}Node cur = root;while(cur!=null){//如果大于data,右边寻找if(cur.val<data){cur = cur.right;}else if(cur.val>data){//小于data,左边寻找cur = cur.left;}else {return true;}}return false;}//插入public void insert(int data){Node node = new Node(data);//如果根节点为空if(root==null){root = node;//根节点为新节点return;}Node cur = root;Node parent = null;while(cur!=null){parent = cur;//存放父节点//向右子树移动if(cur.val<data){cur = cur.right;}else if(cur.val>data){//向左子树移动cur = cur.left;}else{return;//如果val已经存在,直接退出}}//将新节点插入到末尾空节点if(parent.val<data){parent.right = node;}else if(parent.val > data){parent.left = node;}}//删除public boolean remove(int data){if(root==null){return false;}Node cur = root;Node parent = null;//查找datawhile(cur!=null){if(cur.val<data){parent = cur;cur = cur.right;}else if(cur.val>data){parent = cur;cur = cur.left;}else {//删除delete(parent,cur);return true;}}return false;}private void delete(Node parent,Node cur){//如果cur左节点为空if(cur.left==null){//如果cur为根节点if(cur==root){root = cur.right;root.left=null;}//如果cur在左边if(parent.left==cur){parent.left = cur.right;}//如果cur在右边if(parent.right==cur){parent.right=cur.right;}}else if(cur.right==null){//cur右节点为空if(cur==root){root = cur.left;root.right=null;}if(parent.left==cur) {//在左边parent.left = cur.left;}if(parent.right==cur){//在右边parent.right = cur.right;}}else{//左右节点均不为空leftChild(parent,cur);//rightChild(parent,cur);}}//1.找到cur左节点的最右边节点private void leftChild(Node parent,Node cur){parent = cur;Node child = cur.left;while(child.right!=null){parent = child;child = child.right;}//与cur交换,再删除交换后的节点cur.val = child.val;//如果cur左节点没有右孩子if(parent.left==child){parent.left = child.left;}else{parent.right = child.left;}}//2.找到cur右节点的最左边节点private void rightChild(Node parent,Node cur){parent = cur;Node child = cur.right;//cur右节点的最左边节点while(child.left!=null){parent = child;child = child.left;}//与cur交换,再删除交换后的节点cur.val = child.val;//如果cur右节点没有左孩子if(parent.right==child){parent.right = child.right;}else{parent.left = child.right;}}
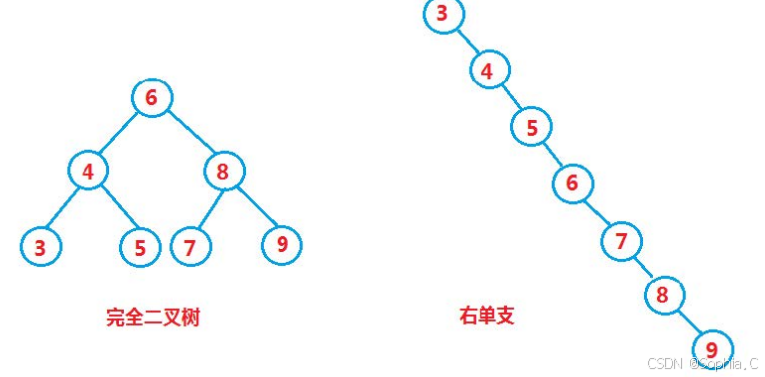
}5. 性能分析
2. 搜索
1. 模型
3. Map 的使用
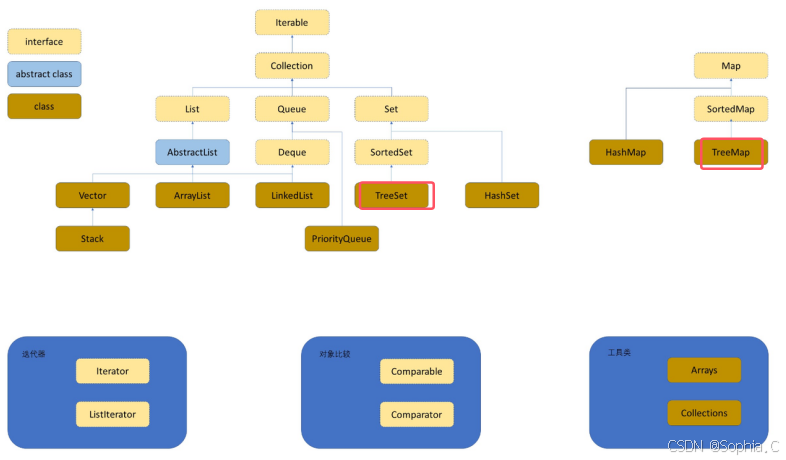
1. 关于Map.Entry<K, V>的说明
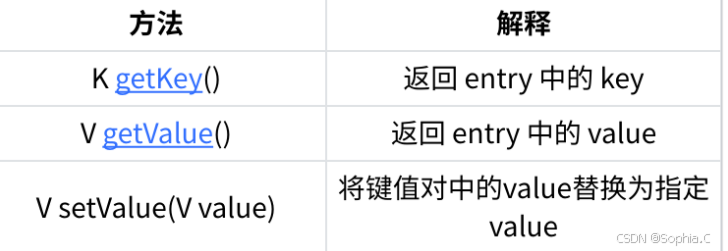
2. Map 的常⽤⽅法

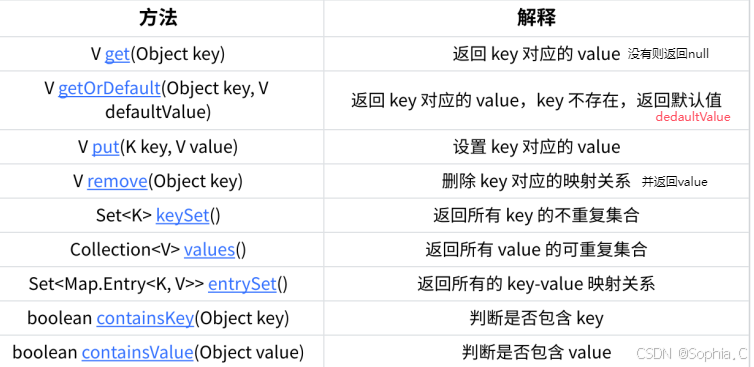
注意:1. Map是⼀个接⼝,不能直接实例化对象,如果要实例化对象只能实例化其实现类TreeMap或者HashMap2. Map中存放键值对的Key是唯⼀的,value是可以重复的3. 在TreeMap中插⼊键值对时,key不能为空,否则就会抛NullPointerException异常,value可以为空。但是HashMap的key和value都可以为空。4. Map中的Key可以全部分离出来,存储到Set中来进⾏访问(因为Key不能重复)。5. Map中的value可以全部分离出来,存储在Collection的任何⼀个⼦集合中(value可能有重复)。6. Map中键值对的Key不能直接修改,value可以修改,如果要修改key,只能先将该key删除掉,然后再来进⾏重新插⼊。
import java.util.Collection;
import java.util.TreeMap;
import java.util.Map;
import java.util.Set;public class TestMap {public static void main(String[] args){Map<String,Integer> map = new TreeMap<>();TreeMap<String,Integer> treeMap = new TreeMap<>();//TreeMap重写了接口Map的所有方法map.put("the",3);map.put("early",5);map.put("bird",4);map.put("catches",7);map.put("the",6);//key已存在,可以改变key对应的value值map.put("worm",4);System.out.println(map.size());//返回此地图中键值映射的数量System.out.println(map.get("the"));//key存在,返回key对应的valueSystem.out.println(map.get("word"));//key不存在,返回nullSystem.out.println(map.getOrDefault("bird",0));//key存在,返回key对应的valueSystem.out.println(map.getOrDefault("time",0));//key不存在,返回自定义valueSystem.out.println(map.remove("the"));//删除key对应的映射关系,并返回key对应的value值System.out.println(map.remove("the"));//key不存在则返回nullSet<String> keyset = map.keySet();//将map中所有的key放入keyset中System.out.println(keyset);for(String s : map.keySet()){System.out.print(s+" ");}System.out.println();Collection<Integer> con =map.values();//将map中所有的value放入con中System.out.println(con);for(Integer cot:map.values()){System.out.print(cot+" ");}System.out.println();//将map中的所有映射关系放入entry中Set<Map.Entry<String,Integer>> entry = map.entrySet();System.out.println(entry);for(Map.Entry<String,Integer> entry1:map.entrySet()){System.out.println("key: "+entry1.getKey()+" ; value: "+entry1.getValue());}}
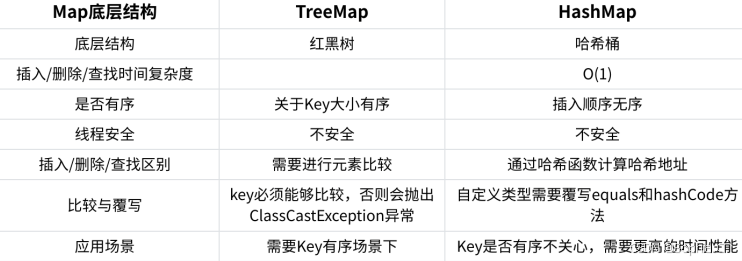
}
4. set 的使用
Set (Java Platform SE 8 )
1. set 的常用方法
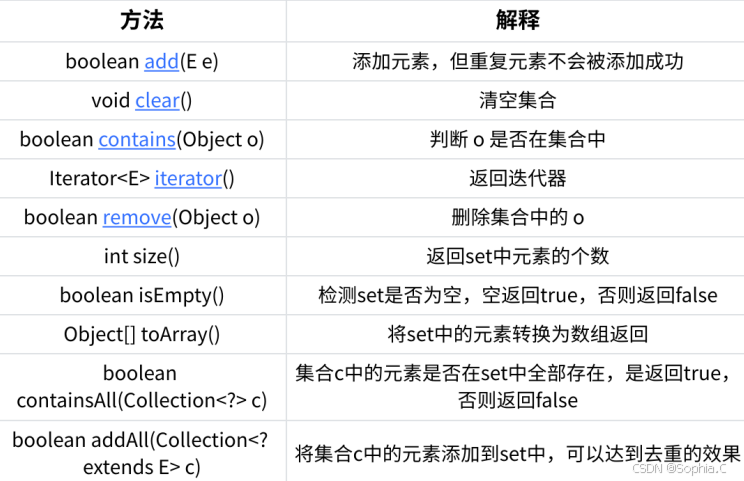
1. Set是继承⾃Collection的⼀个接⼝类2. Set中只存储了key,并且要求key⼀定要唯⼀3. TreeSet的底层是使⽤Map来实现的,其使⽤key与Object的⼀个默认对象作为键值对插⼊到Map中的4. Set最⼤的功能就是对集合中的元素进⾏去重5. 实现Set接⼝的常⽤类有TreeSet和HashSet,还有⼀个LinkedHashSet,LinkedHashSet是在HashSet的基础上维护了⼀个双向链表来记录元素的插⼊次序。6. Set中的Key不能修改,如果要修改,先将原来的删除掉,然后再重新插⼊7. TreeSet中不能插⼊null的key,HashSet可以。
import java.util.*;public class TestSet {public static void main(String[] args) {Set<String> set = new TreeSet<>();TreeSet<String> treeSet = new TreeSet<>();//TreeSet重写了接口set的所有方法//为set添加元素System.out.println(set.add("the"));System.out.println(set.add("early"));System.out.println(set.add("bird"));System.out.println(set.add("catches"));System.out.println(set.add("the"));//key已存在,不添加System.out.println(set.add("worm"));System.out.println(set.size());//返回set中元素的个数System.out.println(set.isEmpty());//判断set是否为空,不为空返回false//判断元素是否存在System.out.println(set.contains("the"));//存在,trueSystem.out.println(set.contains("world"));//不存在,false//删除set中指定的元素System.out.println(set.remove("the"));//存在要删除的元素,删除并返回trueSystem.out.println(set.remove("the"));//不存在要删除的元素,返回false//创建顺序表,作为集合使用ArrayList<String> arrayList = new ArrayList<>();arrayList.add("bird");arrayList.add("worm");判断set是否包含顺序表中的所有元素System.out.println(set.containsAll(arrayList));//包含,truearrayList.add("the");System.out.println(set.containsAll(arrayList));//不包含,false//将set中的元素全部转换为数组String[] s = set.toArray(new String[0]);//原代码直接使用 set.toArray() 会返回 Object[] 而不是 String[]System.out.print(Arrays.toString(s));//打印数组System.out.println();System.out.println(set.addAll(arrayList));//将集合arraylist中的元素添加到set中,重复元素不添加//迭代器Iterator<String> it = set.iterator();while(it.hasNext()){System.out.print(it.next()+" ");}System.out.println();set.clear();//清空集合System.out.println(set.isEmpty());//set为空,返回true}
}

5. 哈希表
1. 概念
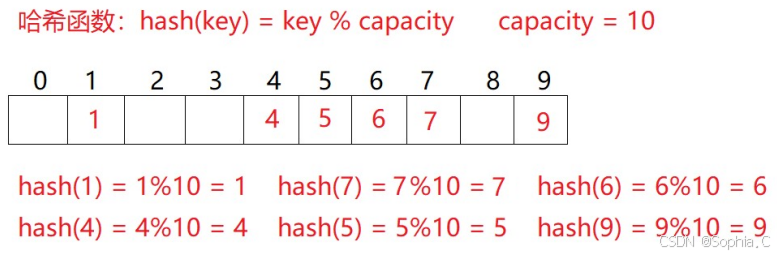
2. 冲突
1. 概念
2. 避免
-哈希函数设计引起哈希冲突的⼀个原因可能是:哈希函数设计不够合理。哈希函数设计原则:• 哈希函数的定义域必须包括需要存储的全部关键码,⽽如果散列表允许有m个地址时,其值域必须在0到m-1之间• 哈希函数计算出来的地址能均匀分布在整个空间中• 哈希函数应该⽐较简单
3. 常⻅哈希函数
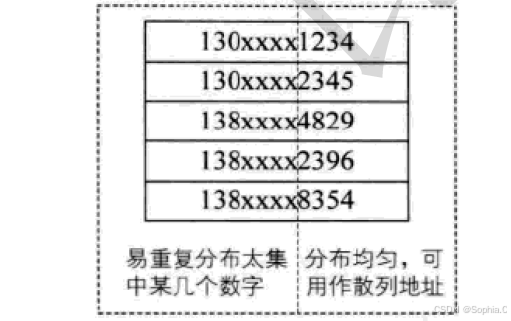
4. 负载因⼦调节

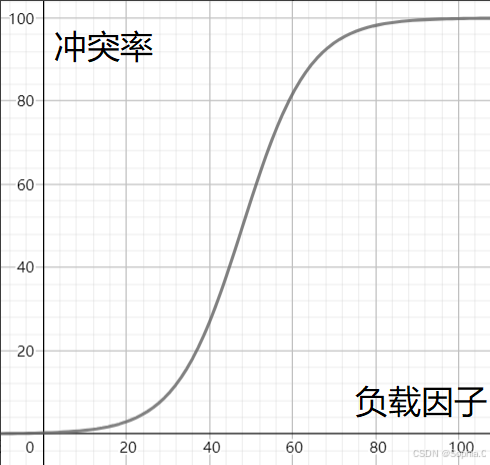
5. 解决
1. 闭散列
1. 线性探测
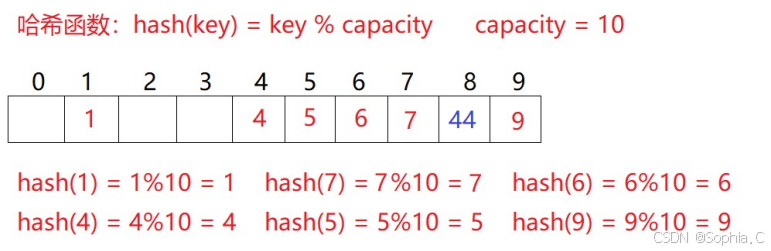
2. ⼆次探测
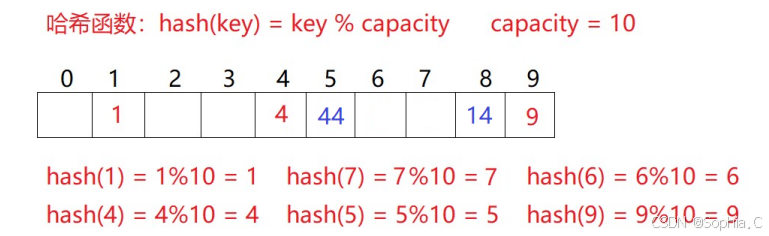
3. 总结
2. 开散列/哈希桶

public class HashBack {//创建节点static class Node{public int key;//存放关键码public int val;//存在value值public Node next;//存在下一个节点的地址//构造方法public Node(int key,int val){this.key = key;this.val = val;}}//创建一个数组,存放具有相同地址的关键码public Node[] arr;//数组中关键码的个数public int usedSize;//构造方法public final int capacity = 1;public HashBack(){this.arr = new Node[capacity];}//插入数据public void put(int keys,int value){//判断负载因子loadFactor();//尾插//lastPut(keys,value);//头插headPut(keys,value);}private void lastPut(int keys,int value){int n = keys % arr.length;//寻找关键码的地址//如果头节点为空,将新节点作为头节点if(arr[n]==null){arr[n] = new Node(keys,value);}else{Node cur = arr[n];Node parent = null;while(cur!=null){parent = cur;//保存当前节点的地址if(cur.key==keys){cur.val = value;//更新value值return ;}cur = cur.next;//更新节点}//创建新节点Node node = new Node(keys,value);parent.next = node;//尾插}usedSize++;}//头插private void headPut(int keys,int value){int n = keys % arr.length;//计算关键码地址Node cur = arr[n];//查找keys是否存在while(cur!=null){if(cur.key == keys){cur.val = value;return;}cur = cur.next;}Node node = new Node(keys,value);//创建新节点//头插node.next = arr[n];arr[n] = node;usedSize++;}//判断负载因子private void loadFactor(){double factor = (usedSize+1)*1.0/arr.length;if(factor<=0.75){return;}//大于0.75,2倍扩容Node[] temp = new Node[2*arr.length];int n = temp.length;//将cur中的节点全部放入temp中for(int i =0;i<arr.length;i++){Node cur = arr[i];while (cur!=null){Node curNext = cur.next;//保存下一个节点地址//计算该cur中的关键码的地址int k = cur.key % n;//头插cur.next = temp[k];temp[k] = cur;cur = curNext;//更新节点}}arr = temp;}//获取keys对应的valpublic int get(int keys){int n = keys % arr.length;Node cur = arr[n];while (cur!=null){if(cur.key == keys){return cur.val;}cur = cur.next;}return -1;}//删除数据public int remove(int keys){//此步骤可以不用,因为在实例化对象时,我们已经将数组实例化,不可能为null
// if(arr==null){
// return -1;
// }int n = keys % arr.length;Node cur = arr[n];Node parent = cur;while(cur!=null){//如果要删除的是头节点if(arr[n].key==keys){arr[n] = arr[n].next;usedSize--;return cur.val;}if(cur.key == keys){parent.next = cur.next;usedSize--;return cur.val;}parent = cur;cur = cur.next;}return -1;}
}key和val不为int类型:需要重写equals和hashcode方法
import java.util.Objects;//创建学生类
class Student{public String name;//构造方法public Student(String name){this.name = name;}//重写equals方法,比较值是否相同@Overridepublic boolean equals(Object o) {if (this == o) return true;if (o == null || getClass() != o.getClass()) return false;Student student = (Student) o;return Objects.equals(name, student.name);}//重写hashCode方法,获取对象地址@Overridepublic int hashCode() {return Objects.hashCode(name);}
}
public class CEHashBack<K,V> {//创建静态内部类,作为节点static class Node<K,V>{public K key;//存放关键码public V val;//存放value值public Node<K,V> next;//存放下一个节点地址//构造方法public Node(K key,V val){this.key = key;this.val = val;}}public Node<K,V>[] arr;//创建存放节点地址数组public int usedSize;//数组中节点个数public final double loadFactor = 0.75;//负载因子的最大值public final int capacity =10;//初始化数组长度//构造方法public CEHashBack(){this.arr = (Node<K, V>[]) new Node[capacity];//实例化数组}//插入(头插)public void put(K key,V val){if(key==null){System.out.println("key为空,无法插入");return;}if((double)(usedSize+1)/arr.length>loadFactor){expansion();//2倍扩容}int hash = Math.abs(key.hashCode());//防止为负数int n = hash % arr.length;//求key对应的数组下标Node<K,V> cur = arr[n];//查找key是否存在while(cur!=null){if(cur.key.equals(key)){cur.val = val;return;}cur = cur.next;}Node<K,V> node = new Node<>(key,val);//创建新节点//头插node.next = arr[n];arr[n] = node;usedSize++;}//2倍扩容private void expansion(){//创建一个新2倍数组Node<K,V>[] temp = (Node<K, V>[])new Node[2*arr.length];//将arr中的节点全部放入temp中for(int i=0;i< arr.length;i++){Node<K,V> cur =arr[i];while(cur!=null){int hash = Math.abs(cur.key.hashCode());//计算关键码的数字地址(防止为负数)int n = hash % temp.length;//在新数组中的下标Node<K,V> curNext = cur.next;//保存下一个节点地址//头插cur.next = temp[n];temp[n] =cur;cur = curNext;//更新节点}}arr = temp;//更新数组arr的地址}//获取key对应的valpublic V get(K key){if(key==null){System.out.print("key为空,无法查找");return null;}int hash = Math.abs(key.hashCode());int n = hash%arr.length;Node<K,V> cur = arr[n];while(cur!=null){if(cur.key.equals(key)){return cur.val;}cur = cur.next;}return null;}//删除public V remove(K key){if(key==null){System.out.print("key为空,无法删除");return null;}int hash = Math.abs(key.hashCode());int n = hash%arr.length;Node<K,V> cur = arr[n];Node<K,V> parent = null;while(cur!=null){//如果要删除头节点if(arr[n].key.equals(key)){arr[n] = arr[n].next;usedSize--;return cur.val;}if(cur.key.equals(key)){parent.next = cur.next;usedSize--;return cur.val;}parent = cur;cur = cur.next;}return null;}
}3. 冲突严重时的解决办法
6. 性能分析
7. 和 java 类集的关系
例题:
138. 随机链表的复制 - 力扣(LeetCode)
相关文章:

数据结构——Map和Set
1. 搜索树 1. 概念 ⼆叉搜索树⼜称⼆叉排序树,它可以是⼀棵空树,或者是具有以下性质的⼆叉树: • 若它的左⼦树不为空,则左⼦树上所有节点的值都⼩于根节点的值 • 若它的右⼦树不为空,则右⼦树上所有节点的值都⼤于根节点的值…...

zsh安装以及安装配置oh-my-zsh安装zsh-autosuggestionszsh-syntax-highlighting
下面是安装 zsh 及配置 oh‑my‑zsh 的详细步骤,适用于 Linux 和 macOS 环境: 1. 安装 zsh 1.1 在 macOS 上安装 zsh macOS 通常预装了 zsh,但建议升级到最新版本。你可以通过 Homebrew 来安装最新版: brew install zsh安装完成…...

VMware 安装 Ubuntu 实战分享
VMware 安装 Ubuntu 实战分享 VMware 是一款强大的虚拟机软件,广泛用于多操作系统环境的搭建。本文将详细介绍如何在 VMware 中安装 Ubuntu,并分享安装过程中的常见问题及解决方法。 1. 安装前的准备工作 (1) 系统要求 主机操作系统:Windo…...

【SpringCloud】Eureka的使用
3. Eureka 3.1 Eureka 介绍 Eureka主要分为两个部分: EurekaServer: 作为注册中心Server端,向微服务应用程序提供服务注册,发现,健康检查等能力。 EurekaClient: 服务提供者,服务启动时,会向 EurekaS…...

Redis:List 类型 内部实现、命令及应用场景
Redis 中的 List(列表)类型是一种有序的数据结构,它可以存储多个字符串元素,并且这些元素按照插入顺序排列。可以将它理解为一个双向链表,支持在链表的两端进行快速的插入和删除操作。它允许元素重复,并且可…...

Python 字符串正则表达式详解
Python 字符串正则表达式详解 一、正则表达式核心语法 元字符含义正确示例与说明常见错误修正.匹配任意字符(换行符除外)a.b → 匹配"acb"、“a1b”不匹配换行符(需用re.S模式)^匹配字符串开头^Hello → 匹配以"H…...

重试机制之指针退避策略算法
一、目的:随着重试次数增加,逐步延长重连等待时间,避免加重服务器负担。 二、计算公式: 每次重试的延迟时间 初始间隔 (退避基数 ^ 重试次数) 通常设置上限防止等待时间过长。 const delay Math.min(initialDelay * Math.pow…...

pyqt第一个窗口程序
文章目录 官方文档相手动创建窗口程序designer创建ui布局 官方文档相 https://doc.qt.io/qtforpython-6/ 手动创建窗口程序 import sys # 导入系统模块,用于获取命令行参数和系统功能 from PySide6.QtWidgets import QApplication, QLabel # 导入Qt组件&#x…...

【蓝桥杯】单片机设计与开发,PWM
一、PWM概述 用来输出特定的模拟电压。 二、PWM的输出 三、例程一:单片机P34引脚输出1kHZ的频率 void Timer0Init(void);unsigned char PWMtt 0;void main(void) {P20XA0;P00X00;P20X80;P00XFF;Timer0Init();EA1;ET01;ET11;while(1);}void Timer0Init(void) //1…...

CSS学习笔记5——渐变属性+盒子模型阶段案例
目录 通俗易懂的解释 渐变的类型 1、线性渐变 渐变过程 2、径向渐变 如何理解CSS的径向渐变,以及其渐变属性 通俗易懂的解释 渐变属性 1. 形状(Shape) 2. 大小(Size) 3. 颜色停靠点(Color Sto…...

频谱分析仪的最大保持功能
专门应用于例如遥控器之类的,按一下,一瞬间出现的信号的测量。 把仪器连接天线,观测空间中的一些信号,比如WIFI的信号,我们可以看到仪器接收到的信号其实是一直变化的,并不是每一次扫描都能扫到我们想要的这…...

权值线段树算法讲解及例题
算法思想 普通的线段树一般是求区间之和或区间最值,所以这些线段树的每个节点的下标是原数组中的区间范围,每个节点存的是区间和或最值,而权值线段树的每个节点的下标是数组中元素的值,而权值线段树每个节点存的是当前元素出现的…...
)
3.26刷题(矩阵模拟专题)
1.59. 螺旋矩阵 II - 力扣(LeetCode) //方法一:变换方向法 class Solution { public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> dirct {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};vector<vect…...
)
深入解析 JSON-RPC:从基础到高级应用(附调用示例)
在当今的软件开发领域,远程过程调用(RPC)技术是实现分布式系统间通信的关键手段之一。JSON-RPC,作为一种基于 JSON 数据格式的轻量级 RPC 协议,因其简洁性和高效性而备受青睐。本文将全面深入地探讨 JSON-RPC 的核心概…...

MAC环境给docker换源
2025-03-28 MAC环境给docker换源 在官网下载docker ,dmg 文件 参考: https://blog.csdn.net/qq_73162098/article/details/145014490 {"builder": {"gc": {"defaultKeepStorage": "20GB","enabled": true}},&q…...

Ollama及HuggingFace路径环境变量设置
日常经常用到这俩的一些环境变量,特记录下来,如有错误,还请指正。 1. Ollama路径环境变量设置 Ollama 模型路径变量名为OLLAMA_MODELS,设置示例: 变量名示例OLLAMA_MODELS C:\Users\Administrator\.ollama\models D…...

Redis | 基于 Redis 实现机器列表 Token 缓存的 Java 实现
关注:CodingTechWork 引言 在分布式系统中,Token 缓存是一种常见的需求。它可以帮助我们快速验证用户身份,减少对数据库的频繁访问,提高系统的性能和响应速度。本文将介绍如何使用 Redis 来实现机器列表的 Token 缓存,…...

Linux\CentOS解决OpenSSH和Nginx安全漏洞
前言 由于有些服务器需要对公网提供服务、客户对于服务器安全比较重视,需要公司提供服务器安全报告。大多数服务器经过漏洞扫描之后、会出现很多软件低版本的漏洞,此时就需要升级软件的版本来解决这些漏洞问题。本篇文章记录升级软件过程。 漏洞编号漏…...

ubuntu22.04 ROS2humble 路径文件
ROS2humble 路径文件 /opt/ros/humble/include/opt/ros/humble/lib/opt/ros/humble/share 下载ros2之后会有下面的文件,在/opt/ros/humble下 /opt/ros/humble/include C/C 头文件(.h, .hpp) /opt/ros/humble/lib 作用: 存放 编译生成的二…...

zookeeper部署教程
在Linux系统中离线安装并配置ZooKeeper,可按以下步骤操作: 1. 准备安装包和依赖 下载ZooKeeper:在有网络的环境下,前往Apache ZooKeeper官网下载所需的稳定版本,例如zookeeper-3.8.2.tar.gz。准备JDK:Zoo…...

生成信息提取的大型语言模型综述
摘要 信息提取(IE)旨在从简单的自然语言文本中提取结构知识。最近,生成型大型语言模型(LLMs)在文本理解和生成方面表现出了显著的能力。因此,已经提出了许多基于生成范式将LLM集成到IE任务中的工作。为了对…...
任务脚本)
霸王茶姬小程序(2025年1月版)任务脚本
脚本用于自动执行微信小程序霸王茶姬的日常签到和积分管理任务。 脚本概述 脚本设置了定时任务(cron),每天运行两次,主要用于自动签到以获取积分,积分可以用来换取优惠券。 核心方法 constructor:构造函数,用于初始化网络请求的配置,设置了基础的 HTTP 请求头等。 logi…...

Maven中为什么有些依赖不用引入版本号
先给出一个例子: <parent><artifactId>sky-take-out</artifactId><groupId>com.sky</groupId><version>1.0-SNAPSHOT</version></parent><modelVersion>4.0.0</modelVersion><artifactId>sky-s…...
、调参方法)
机器学习——集成学习框架(GBDT、XGBoost、LightGBM、CatBoost)、调参方法
一、集成学习框架 对训练样本较少的结构化数据领域,Boosting算法仍然是常用项 XGBoost、CatBoost和LightGBM都是以决策树为基础的集成学习框架 三个学习框架的发展是:XGBoost是在GBDT的基础上优化而来,CatBoost和LightGBM是在XGBoost的基础上…...

第十二章——位运算
按位的与& 若x的第i位和y的第i位都是1,那么(x&y)1,否则(x&y) 0 应用:希望让某一位或某些位为0 。取一个数中的一段。 按位的或| 若x的第i位1或y的第i位1,那么&…...

陪伴就诊 APP 功能架构:如何通过特定模块筛选优秀陪诊师
在当今社会,随着人们对医疗服务品质需求的提升,陪诊师这一职业应运而生。然而,市场上陪诊师众多,水平参差不齐,如何筛选出优秀的陪诊师成了大家关注的焦点。而陪伴就诊 APP 的等级功能,为我们提供了一个有效…...
:如何解决用户的质疑?)
UI产品经理基础(六):如何解决用户的质疑?
在需求调查中遇到用户质疑“不专业”或“不了解需求”,本质上是用户对产品经理的信任缺失或沟通鸿沟导致的。要化解这种质疑,需从专业能力展示、沟通方式优化、用户参与感提升三个维度切入,结合具体场景采取针对性策略。以下是系统化的解决方…...
)
【江协科技STM32】BKP备寄存器RTC实时时钟(学习笔记)
BKP备寄存器 BKP简介 BKP(Backup Registers)备份寄存器BKP可用于存储用户应用程序数据。当VDD(2.0~3.6V)电源被切断,他们仍然由VBAT(1.8~3.6V)维持供电。当系统在待机模式下被唤醒࿰…...

Flutter项目之table页面实现
目录: 1、首页页面index.dart(首页table页面)searchbar.dart (搜索页面)common_swiper.dart (轮播图)index_navigation.dart (导航区域)index_navigatorItem_list.dart (数组构造) 2、房屋推荐index_recommond.dart (房屋推荐区域)IndexRecom…...

Stable Virtual Camera 重新定义3D内容生成,解锁图像新维度;BatteryLife助力更精准预测电池寿命
在数字内容创作的激烈竞争中,Stability AI 正站在命运的十字路口。这家曾以 Stable Diffusion 引爆图像生成革命的公司,却因上层管理问题陷入了危机。近期,Stability AI 推出了 Stable Virtual Camera 模型,不知能否以一记重拳打破…...

物理安全——问答
目录 1、计算机的物理安全包含哪些内容 1. 设备保护 2. 访问控制 3. 电力与环境安全 4. 数据存储保护 5. 硬件防护 6. 监控与审计 7. 灾难恢复与应急响应 8. 拆卸与维修安全 2、物理安全有哪些需要关注的问题 1、计算机的物理安全包含哪些内容 1. 设备保护 防止盗窃&…...

「查缺补漏」巩固你的 RabbitMQ 知识体系
1 MQ 存在的意义 消息中间件一般主要用来做 异步处理、应用解耦、流量削峰、日志处理 等方面。 1.1 异步处理 一个用户登陆网址注册,然后系统发短信跟邮件告知注册成功,一般有三种解决方法。 串行方式,依次执行,问题是用户注册…...

前后前缀
一种特殊的前缀方法: 通过前后两次前缀,可以求出目的区间值 例题1: 最大或值:2680. 最大或值 - 力扣(LeetCode)(贪心前缀) 贪心可知只让一个数变化最后或值最大,所以通过…...

C++细节知识for面试
1. linux上C程序可用的栈和堆大小分别是多少,为什么栈大小小于堆? 1. 栈(Stack)大小 栈默认为8MB,可修改。 为什么是这个大小: 安全性:限制栈大小可防止无限递归或过深的函数调用导致内存…...

构建高可用性西门子Camstar服务守护者:异常监控与自愈实践
在智能制造领域,西门子Camstar作为领先的MES系统承载着关键生产业务。但在实际运维中,我们发现其服务常因数据库负载激增(如SQL阻塞链超时)或应用服务器资源耗尽(CPU峰值达90%以上)导致服务不可用。传统人工干预方式平均故障恢复时间长达47分钟,这对连续生产场景构成了严…...

DeepSeek-V3-250324: AI模型新突破,性能超越GPT-4.5
DeepSeek 于 3 月 25 日宣布完成 V3 模型的小版本升级,推出 DeepSeek-V3-250324 版本。新版本在推理能力、代码生成、中文写作及多模态任务上实现显著优化,尤其在数学和代码类评测中得分超越 GPT-4.5,引发行业高度关注。 DeepSeek-V3-250324…...

OSPF邻居状态机
OSPF(Open Shortest Path First)协议的邻接关系状态机描述了两台OSPF路由器之间建立和维护邻接关系的过程。以下是每个状态的简要描述: Down State(关闭状态) 描述:这是OSPF邻接关系的初始状态,…...

使用tensorflow实现线性回归
目录 前言使用TensorFlow实现算法的基本套路:实战 前言 实现一个算法主要从以下三步入手: 找到这个算法的预测函数, 比如线性回归的预测函数形式为:y wx b, 找到这个算法的损失函数 , 比如线性回归算法的损失函数为最小二乘法 找到让损失函数求得最小值的时候的系数, 这时一…...
)
CF每日5题Day4(1400)
好困,感觉很累,今天想赶紧写完题早睡。睡眠不足感觉做题都慢了。 1- 1761C 构造 void solve(){int n;cin>>n;vector<vector<int>>a(n1);forr(i,1,n){//保证每个集合不同a[i].push_back(i);}forr(i,1,n){string s;cin>>s;forr(…...

Vala 编程语言教程-继承
继承 在 Vala 中,一个类可以继承自 一个或零个 其他类。尽管实际开发中通常继承一个类(不同于 Java 等语言的隐式继承机制),但 Vala 并不强制要求必须继承。 当定义继承自其他类的子类时,子类的实例与父…...
)
CLion下载安装(Windows11)
目录 CLion工具下载安装其他 CLion CLion-2024.1.4.exe 工具 系统:Windows 11 下载 1.通过百度网盘分享的文件:CLion-2024.1.4.exe 链接:https://pan.baidu.com/s/1-zH0rZPCZtQ60IqdHA7Cew?pwdux5a 提取码:ux5a 安装 打开…...
)
QEMU源码全解析 —— 块设备虚拟化(12)
接前一篇文章:QEMU源码全解析 —— 块设备虚拟化(11) 本文内容参考: 《趣谈Linux操作系统》 —— 刘超,极客时间 《QEMU/KVM源码解析与应用》 —— 李强,机械工业出版社 特此致谢! QEMU初始化阶段的块设备虚拟化 从模板生成类和类的实例化 本回继续解析QEMU类Java反…...
 来查看安卓 Logcat 日志)
如何使用VS中的Android Game Development Extension (AGDE) 来查看安卓 Logcat 日志
一、首先按照以下 指引 中的 第1、2步骤,安装一下 AGDE ,AGDE 的安装包可以在官网上找到。 UE4 使用AndroidGameDevelopmentExtension(AGDE)对安卓客户端做“断点调试”与“代码热更”-CSDN博客 在执行第二步骤前,记得…...

Z字形变换
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。 比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下: P A H N A P L S I I G Y I R 之后,你的输出需要从左往右…...

跟着尚硅谷学vue-day1
前言:企业多用vue3,但是考虑到时间较充足,先学vue2,学vue3较为方便。 1.vue是什么? 一套用于构建用户界面的渐进式Javascript 框架 构建用户界面:数据->界面 渐进式:Vue可以自底向上逐层的应用 简单应用: 只需一个轻量小…...

平板实现 adb connect 连接的步骤
1. 检查设备的开发者选项 确保平板设备已开启开发者模式,并启用了USB调试。 2. 检查设备和电脑的网络连接 确保平板和电脑连接到同一个Wi-Fi网络,确认设备的 IP 地址是否正确。 通过 ping 命令测试: ping 192.168.3.243. 通过USB线进行初…...

VUE3+TypeScript项目,使用html2Canvas+jspdf生成PDF并实现--分页--页眉--页尾
使用html2CanvasJsPDF生成pdf,并实现分页添加页眉页尾 1.封装方法htmlToPdfPage.ts /**path: src/utils/htmlToPdfPage.tsname: 导出页面为PDF格式 并添加页眉页尾 **/ /*** 封装思路* 1.将页面根据A4大小分隔边距,避免内容被中间截断* 所有元素层级不要…...

windows第十八章 菜单、工具栏、状态栏
文章目录 创建框架窗口菜单菜单的风格通过资源创建菜单菜单的各种使用通过代码创建菜单在鼠标位置右键弹出菜单 CMenu常用函数介绍工具栏方式一,从资源创建工具栏方式二,代码创建 状态栏状态栏基础创建状态栏 创建框架窗口 手动创建一个空项目ÿ…...

C语言中的位域:节省内存的标志位管理技术
位域(Bit-field) 是 C 语言中的一种特性,允许在结构体(struct)中定义占用特定位数的成员变量。通过位域,可以更精细地控制内存的使用,尤其是在需要存储多个布尔值或小范围整数时,可以…...

单端信号差分信号
单端信号和差分信号是电路中常见的两种信号传输方式,它们在具体的应用场景和特点上有着明显的区别。下面就来详细说明一下单端信号和差分信号的区别。 首先,单端信号是指信号通过一个信号线传输,通常一个信号线携带一个信号。这种传输方式适…...
